Physique quantique for dummies
+32
Topsy Turvy
Opossum
Seskap
Mentounasc
câlin
Shadow Boxeur
doom
tim9.5
Stegos
siamois93
I am So Sure
LhaleeTreize
Iron D. Tramb
Ardel
AcideMatt
fift
jaravan
Le champ de l'abstraction
Ramen Taf'
i.a.
DLS
Tokamak
Like a Frog
REGBEL
prométhéus
ortolan
Darth Lord Tiger Kalthu
paela
bepo
Badak
Patate
Confiteor
36 participants
Page 9 sur 16
Page 9 sur 16 •  1 ... 6 ... 8, 9, 10 ... 12 ... 16
1 ... 6 ... 8, 9, 10 ... 12 ... 16 
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Ha bah après l'"extrapolation" en question est tout un formalisme mathématique qu'il faut utiliser, avec ses hypothèses et la rigueur nécessaire à son accomplissement. Par exemple l'approche de Boltzmann d'évènements à l'échelle quantique a créé la mécanique des fluides (donc à l'échelle mésoscopique, i.e. intermédiaire entre le macro et le micro), mais les hypothèses nécessaires à son élaboration montre les limites. Ne pas connaître ces hypothèses et ces limites permet de faire dire n'importe quoi à ces modèles à qui ne connaît pas et n'a jamais mis les mains dans le cambouis...
Pour le reste, c'est sur que ça fait briller en société de sortir "quantique", "Einstein", "révolutionnaire", et "espace-temps" dans la mème phrase. De là à ce que ça veuille dire quelque chose... pour le moment je n'ai jamais vu (fonctionne aussi avec "quantique", "médical", "mémoire de l'eau" et autres débilités du genre).
Pour le reste, c'est sur que ça fait briller en société de sortir "quantique", "Einstein", "révolutionnaire", et "espace-temps" dans la mème phrase. De là à ce que ça veuille dire quelque chose... pour le moment je n'ai jamais vu (fonctionne aussi avec "quantique", "médical", "mémoire de l'eau" et autres débilités du genre).
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien (suite de la page 17)
L'oscillateur harmonique
Le modèle des petits mouvements presque sur place se nomme l'oscillateur.

Prenons le cas d'un objet qui fait des va-et-viens horizontalement, grâce à un ressort attaché à une paroi. (On fait donc de la mécanique classique.)
L'énergie cinétique (de mouvement) est égal à la vitesse de l'objet au carré, fois ce qu'il pèse.
L'énergie potentielle est l'énergie reliée au ressort.
Ces énergies varient tout le temps, mais leur somme reste constante. Le parallélépiède de droite qui ne change jamais de forme, malgré le changement de couleur rapide. C'est l'hamiltonien, l'énergie totale du système.
Quand le cube est tout à gauche (ou tout à droite), son énergie cinétique est nulle, tandis que sont énergie potentielle est au plus haut : il est prêt à partir dans l'autre sens.
Quand le cube est au centre, son énergie cinétique est au plus haut, tandis que son énergie potentielle est nulle : le ressort ne freine ni ne pousse l'objet à cet endroit.
Les points noirs indiquent la position de l'objet chaque fraction de seconde. Afin d'éviter d'avoir une ligne toute noire horizontale qui indique sa position, on décale à chaque fois un peu le tracé vers le haut.
On obtient ainsi un graphique espace-temps. (l'espace est l'axe horizontal, et le temps l'axe vertical).
La trajectoire noire décrit une ondulation (on peut la modéliser avec une fonction sinus). Les points sont très serrés dans les bords, c'est là qu'on à plus de chance de trouver notre objet. Au centre les points sont espacés au maximum, signe de grande vitesse pour l'objet. On a moins de chance de le trouver que dans les bords.
La flèche du bas indique que l'objet est attiré par la planète. La flèche du haut est de même taille que celle du bas. Elle indique que la table compense la chute de l'objet. La flèche rose indique l'action du ressort qui modifie la trajectoire de l'objet. Une flèche opposée, plus petite, modélise les frottements entre l'objet et la table. Dans la réalité il y a toujours des pertes d'énergie sous forme de chaleur, ce qui fera ralentir puis immobiliser l'objet. Dans ce cas l'hamiltonien (le pavé à droite) diminue régulièrement. Pourtant l'énergie n'est pas détruite, elle est simplement hors du radar. Dans ce cas l'énergie de l'objet + du ressort + du labo reste constante, pour autant que le labo soit isolé de toute influence.
Les oscillateurs harmoniques sont toujours sans frottement : ils modélisent des mouvements qui n'existent pas dans la réalité, et servent d'approximation. Si on veut rajouter les frottements, le modèle se nomme oscillateur harmonique amorti.
Le même modèle mathématique s'utilise pour les pendules : (ici Em = notre hamiltonien, ou énergie mécanique).
La suite de ce post, avec des objets de dix puissance moins neuf mètres.
L'oscillateur harmonique
Le modèle des petits mouvements presque sur place se nomme l'oscillateur.

Prenons le cas d'un objet qui fait des va-et-viens horizontalement, grâce à un ressort attaché à une paroi. (On fait donc de la mécanique classique.)
L'énergie cinétique (de mouvement) est égal à la vitesse de l'objet au carré, fois ce qu'il pèse.
L'énergie potentielle est l'énergie reliée au ressort.
Ces énergies varient tout le temps, mais leur somme reste constante. Le parallélépiède de droite qui ne change jamais de forme, malgré le changement de couleur rapide. C'est l'hamiltonien, l'énergie totale du système.
Quand le cube est tout à gauche (ou tout à droite), son énergie cinétique est nulle, tandis que sont énergie potentielle est au plus haut : il est prêt à partir dans l'autre sens.
Quand le cube est au centre, son énergie cinétique est au plus haut, tandis que son énergie potentielle est nulle : le ressort ne freine ni ne pousse l'objet à cet endroit.
Les points noirs indiquent la position de l'objet chaque fraction de seconde. Afin d'éviter d'avoir une ligne toute noire horizontale qui indique sa position, on décale à chaque fois un peu le tracé vers le haut.
On obtient ainsi un graphique espace-temps. (l'espace est l'axe horizontal, et le temps l'axe vertical).
La trajectoire noire décrit une ondulation (on peut la modéliser avec une fonction sinus). Les points sont très serrés dans les bords, c'est là qu'on à plus de chance de trouver notre objet. Au centre les points sont espacés au maximum, signe de grande vitesse pour l'objet. On a moins de chance de le trouver que dans les bords.
La flèche du bas indique que l'objet est attiré par la planète. La flèche du haut est de même taille que celle du bas. Elle indique que la table compense la chute de l'objet. La flèche rose indique l'action du ressort qui modifie la trajectoire de l'objet. Une flèche opposée, plus petite, modélise les frottements entre l'objet et la table. Dans la réalité il y a toujours des pertes d'énergie sous forme de chaleur, ce qui fera ralentir puis immobiliser l'objet. Dans ce cas l'hamiltonien (le pavé à droite) diminue régulièrement. Pourtant l'énergie n'est pas détruite, elle est simplement hors du radar. Dans ce cas l'énergie de l'objet + du ressort + du labo reste constante, pour autant que le labo soit isolé de toute influence.
Les oscillateurs harmoniques sont toujours sans frottement : ils modélisent des mouvements qui n'existent pas dans la réalité, et servent d'approximation. Si on veut rajouter les frottements, le modèle se nomme oscillateur harmonique amorti.
Le même modèle mathématique s'utilise pour les pendules : (ici Em = notre hamiltonien, ou énergie mécanique).
La suite de ce post, avec des objets de dix puissance moins neuf mètres.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
Le concept de l'énergie
L'énergie est une grande famille : étimologiquement force en action, puis énergie cinétique, potentielle, magnétique, spirituelle, du matin, antonyme de la fatigue, structure vibratoire, psycho-kinetique, raiki, primaire, etc.
La physique a ses critères de tri :
a) une énergie doit être mesurable par un appareil. Adieu donc à celles détectés uniquement par des êtres humains.
b) elle doit pouvoir s'échanger avec d'autres énergies, à taux fixe 1:1. une "pièce" d'énergie potentielle peut se changer en une "pièce" d'énergie cinétique par exemple.
c) la quantité totale d'énergies à l'instant t reste la même un instant plus tard. C'est le principe de conservation d'énergie, ou principe d'invariance par translation (dans le temps). Ce principe est représenté par l'hamiltonien dans la vidéo ci-dessus : il y a échange constant entre l'énergie cinétique et potentielle dans le mouvement de l'objet, mais la hauteur du pavé droit reste constant dans le temps. (On peut relier le bilan énergétique du cube avec l'amplitude de son déplacement, plus l'amplitude est grande, plus l'énergie de départ du sytème doit être grande).
Les énergies en physique peuvent être vues comme des devises mesurables qui s'échangent entre elles, pas nécessairement de manière directe. Une énergie radioactive peut se changer en chaleur qui sera changée en mouvement puis en énergie électrique : c'est le schéma suivi par une centrale nucléaire dont l'électricité te sert peut-être à me lire actuellement.

(Le réacteur n'est rien d'autre qu'une piscine d'eau chauffée par des crayons d'uranium en activité et pilotés.)
Des objets transformant une énergie en une autre possède un rendement = l'énergie utile divisée par l'énergie de départ. Une lampe à filament et un four sont identiques au point de vue énergétique : c'est un métal chauffé. Ils utilisent tout deux de l'électricité et fournissent tout deux de l'énergie calorifique (95%) et de l'énergie lumineuse (5%) (Je ne parle pas de la lampe du four, mais du cordon de chauffe. On le voit s'illuminer dans un four à raclette par exemple).
Quel est le rendement de la lampe ? 5% car c'est la lumière qui nous intéresse. Et le four : 95% car c'est la chaleur qui est dans ce cas l'énergie utile. Mais rien ne t'empêche d'utiliser une lampe pour cuire la paume de ta main par exemple.
L'énergie électrique est la plus pratique mais peu stockable (elle n'est pas stockée dans les piles, c'est de l'énergie chimique en fait) L'énergie calorifique est celle qui apparaît le plus souvent sous forme inutilisable (c'est dû aux frottements, à la chaleur emmagasinée par la casserole pour pouvoir y chauffer l'eau, etc.)
L'énergie est un concept qui a évolué sur plusieurs siècles. Elle n'est pas définissable en tant que tel, mais toute énergie en physique s'écrit sous forme d'équation.
Par exemple ta masse te confère une énergie de masse quantifiée par le fameux e=mc².
Partie de l'énergie de mouvement on a rajouté des formes d'énergies afin de sauvegarder le principe de conservation d'énergie au fur et au mesure des découvertes scientifiques. Ce point de vue d'un physicien, Luc Valentin, a permis la forge de nombres constants artificiels : "Par exemple, la constante J = 4,18 Joule/calorie, appelée équivalent mécanique de la calorie, fait que l'on peut exprimer par un nombre "sans odeur, sans saveur, etc." des choses aussi différentes, a priori, que la chaleur et l'énergie mécanique associées qualitativement aux sensations de chaud et de froid, d'une part (énergie thermique), et d'autre part aux déplacements dans l'espace-temps (énergie cinétique) ou à leurs virtualités (énergie potentielle)."
Dans le cas quantique qui nous intéresse : "En mécanique quantique, c'est la constante de Planck, h, qui permet d'unifier les facettes corpusculaires et ondulatoires des phénomènes, grâce, par exemple, à la relation d'Einstein, E = hn, où E est l'énergie du corpuscule et où n est la fréquence de l'onde qui lui est associée." (ibid.)
A la question "pourquoi la nature accepte-t-elle de se plier à des principes d'invariance?", "l'artificialiste répond que les physiciens interprètent la nature en la réduisant à des nombres, et le naturaliste ajoute qu'ils arrivent à le faire parce que nous existons ici et maintenant avec nos sensations. Au lecteur de prendre conscience de sa propre philosophie" (ibid.)
Une énergie pourtant est prise en compte par les physiciens, alors qu'elle ne remplit pas tous les critères ci-dessus : l'énergie noire. On ne peut la mesurer directement, mais elle pèserait en moyenne 10 puissance −29 g/cm3 et répartie partout dans l'univers.
Lorsque je jette une balle dans le jardin aussi vite que la balle d'un pistolet, je ne puis expliquer cela par les moyens physiques classiques. C'est ce qui s'est passé lorsqu'on a mesuré l'accélération de l'expension de notre univers, qui n'est pas une accélération normale. On postule donc une énergie sombre qui compose presque les 3/4 de l'univers !

Ce graphique de répartition d'énergie réduit à 5% la partie connue par l'être humain : 5% de la composition de l'univers ! Incroyable.
Pour approfondir la compréhension de l'énergie et du principe de conservation : http://gric.univ-lyon2.fr/gric3/decouverte/document/texthistorique/texteshistenergie.html
Notamment :
- le principe de conservation : la comparaison de Feynman (toujours excellent) avec les échecs + le texte complet de Luc Valentin
- la conservation d'énergie de Feynman à l'aide d'une comparaison avec des cubes d'enfant + l'article de Bernard d'Espagnat.
Le concept de l'énergie
L'énergie est une grande famille : étimologiquement force en action, puis énergie cinétique, potentielle, magnétique, spirituelle, du matin, antonyme de la fatigue, structure vibratoire, psycho-kinetique, raiki, primaire, etc.
La physique a ses critères de tri :
a) une énergie doit être mesurable par un appareil. Adieu donc à celles détectés uniquement par des êtres humains.
b) elle doit pouvoir s'échanger avec d'autres énergies, à taux fixe 1:1. une "pièce" d'énergie potentielle peut se changer en une "pièce" d'énergie cinétique par exemple.
c) la quantité totale d'énergies à l'instant t reste la même un instant plus tard. C'est le principe de conservation d'énergie, ou principe d'invariance par translation (dans le temps). Ce principe est représenté par l'hamiltonien dans la vidéo ci-dessus : il y a échange constant entre l'énergie cinétique et potentielle dans le mouvement de l'objet, mais la hauteur du pavé droit reste constant dans le temps. (On peut relier le bilan énergétique du cube avec l'amplitude de son déplacement, plus l'amplitude est grande, plus l'énergie de départ du sytème doit être grande).
Les énergies en physique peuvent être vues comme des devises mesurables qui s'échangent entre elles, pas nécessairement de manière directe. Une énergie radioactive peut se changer en chaleur qui sera changée en mouvement puis en énergie électrique : c'est le schéma suivi par une centrale nucléaire dont l'électricité te sert peut-être à me lire actuellement.

(Le réacteur n'est rien d'autre qu'une piscine d'eau chauffée par des crayons d'uranium en activité et pilotés.)
Des objets transformant une énergie en une autre possède un rendement = l'énergie utile divisée par l'énergie de départ. Une lampe à filament et un four sont identiques au point de vue énergétique : c'est un métal chauffé. Ils utilisent tout deux de l'électricité et fournissent tout deux de l'énergie calorifique (95%) et de l'énergie lumineuse (5%) (Je ne parle pas de la lampe du four, mais du cordon de chauffe. On le voit s'illuminer dans un four à raclette par exemple).
Quel est le rendement de la lampe ? 5% car c'est la lumière qui nous intéresse. Et le four : 95% car c'est la chaleur qui est dans ce cas l'énergie utile. Mais rien ne t'empêche d'utiliser une lampe pour cuire la paume de ta main par exemple.
L'énergie électrique est la plus pratique mais peu stockable (elle n'est pas stockée dans les piles, c'est de l'énergie chimique en fait) L'énergie calorifique est celle qui apparaît le plus souvent sous forme inutilisable (c'est dû aux frottements, à la chaleur emmagasinée par la casserole pour pouvoir y chauffer l'eau, etc.)
L'énergie est un concept qui a évolué sur plusieurs siècles. Elle n'est pas définissable en tant que tel, mais toute énergie en physique s'écrit sous forme d'équation.
Par exemple ta masse te confère une énergie de masse quantifiée par le fameux e=mc².
Partie de l'énergie de mouvement on a rajouté des formes d'énergies afin de sauvegarder le principe de conservation d'énergie au fur et au mesure des découvertes scientifiques. Ce point de vue d'un physicien, Luc Valentin, a permis la forge de nombres constants artificiels : "Par exemple, la constante J = 4,18 Joule/calorie, appelée équivalent mécanique de la calorie, fait que l'on peut exprimer par un nombre "sans odeur, sans saveur, etc." des choses aussi différentes, a priori, que la chaleur et l'énergie mécanique associées qualitativement aux sensations de chaud et de froid, d'une part (énergie thermique), et d'autre part aux déplacements dans l'espace-temps (énergie cinétique) ou à leurs virtualités (énergie potentielle)."
Dans le cas quantique qui nous intéresse : "En mécanique quantique, c'est la constante de Planck, h, qui permet d'unifier les facettes corpusculaires et ondulatoires des phénomènes, grâce, par exemple, à la relation d'Einstein, E = hn, où E est l'énergie du corpuscule et où n est la fréquence de l'onde qui lui est associée." (ibid.)
A la question "pourquoi la nature accepte-t-elle de se plier à des principes d'invariance?", "l'artificialiste répond que les physiciens interprètent la nature en la réduisant à des nombres, et le naturaliste ajoute qu'ils arrivent à le faire parce que nous existons ici et maintenant avec nos sensations. Au lecteur de prendre conscience de sa propre philosophie" (ibid.)
Une énergie pourtant est prise en compte par les physiciens, alors qu'elle ne remplit pas tous les critères ci-dessus : l'énergie noire. On ne peut la mesurer directement, mais elle pèserait en moyenne 10 puissance −29 g/cm3 et répartie partout dans l'univers.
Lorsque je jette une balle dans le jardin aussi vite que la balle d'un pistolet, je ne puis expliquer cela par les moyens physiques classiques. C'est ce qui s'est passé lorsqu'on a mesuré l'accélération de l'expension de notre univers, qui n'est pas une accélération normale. On postule donc une énergie sombre qui compose presque les 3/4 de l'univers !

Ce graphique de répartition d'énergie réduit à 5% la partie connue par l'être humain : 5% de la composition de l'univers ! Incroyable.
Pour approfondir la compréhension de l'énergie et du principe de conservation : http://gric.univ-lyon2.fr/gric3/decouverte/document/texthistorique/texteshistenergie.html
Notamment :
- le principe de conservation : la comparaison de Feynman (toujours excellent) avec les échecs + le texte complet de Luc Valentin
- la conservation d'énergie de Feynman à l'aide d'une comparaison avec des cubes d'enfant + l'article de Bernard d'Espagnat.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Mise à jour sur l'énergie noire
Une hypothèse a été proposée par un chercheur de l'université de Genève : l'invariance des propriétés du vide. Quand le vide est contracté ou dilaté, ses propriétés ne changent pas.
En tenant compte de cette contrainte, l'auteur revisite les équations d'Einstein. Pour lui, le vide s'y cache dans la fameuse constante cosmologique. Cette invariance se trouve aussi dans la théorie fondamentale de l'électromagnétisme (qui décrit la lumière par exemple).
En simulant la formation de galaxies avec son modèle, il obtient des résultats très proches des observations réelles.
Pour lui, point d'énergie noire, point de matière noire.
De plus, son modèle prédit la dispersion des étoiles qui oscillent autour de notre voie lactée, ce qu'aucun modèle n'a pu faire auparavant.
https://www.unige.ch/sciences/astro/fr/news/matiere-noire-et-energie-noire-remise-en-question/
"«L’annonce de ce modèle, qui finalement résout deux grands mystères de l’astronomie, reste fidèle à l’esprit de la science: rien n’est jamais acquis, ni sur le plan de l’expérience ou de l’observation, ni sur celui du raisonnement de l’être humain», conclut l’astronome genevois."
Une hypothèse a été proposée par un chercheur de l'université de Genève : l'invariance des propriétés du vide. Quand le vide est contracté ou dilaté, ses propriétés ne changent pas.
En tenant compte de cette contrainte, l'auteur revisite les équations d'Einstein. Pour lui, le vide s'y cache dans la fameuse constante cosmologique. Cette invariance se trouve aussi dans la théorie fondamentale de l'électromagnétisme (qui décrit la lumière par exemple).
En simulant la formation de galaxies avec son modèle, il obtient des résultats très proches des observations réelles.
Pour lui, point d'énergie noire, point de matière noire.
De plus, son modèle prédit la dispersion des étoiles qui oscillent autour de notre voie lactée, ce qu'aucun modèle n'a pu faire auparavant.
https://www.unige.ch/sciences/astro/fr/news/matiere-noire-et-energie-noire-remise-en-question/
"«L’annonce de ce modèle, qui finalement résout deux grands mystères de l’astronomie, reste fidèle à l’esprit de la science: rien n’est jamais acquis, ni sur le plan de l’expérience ou de l’observation, ni sur celui du raisonnement de l’être humain», conclut l’astronome genevois."

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
Comparaison d'un oscillateur classique et d'un oscillateur quantique
Je vous propose aujourd'hui un montage vidéo pour bien comprendre la différence entre notre monde habituel et le monde quantique.
Doug modélise un objet qui fait des va-et-vient (comme une balançoire, ou un objet attaché à un ressort qu'on n'a pas représenté) le long d'une droite, par une boule bleue. Son mouvement est limité vers la gauche et vers la droite. On dit que ce mouvement a un degré de liberté : il ne peut ni aller vers le haut, ni vers nous. C'est pourquoi le tube de pvc contenant la balle modélise la contrainte du mouvement.
A 0:16, la vidéo propose une suite de photographies prise à intervalle de temps régulier afin de capturer le mouvement.
Observations :
-il est facile de prévoir le lieu de la balle, l'instant suivant;
- au centre du tube la balle passe très vite;
- au bord sa vitesse diminue, jusqu'à être nulle au bord, avant de partir en sens inverse.
(Je laisse de côté la vidéo à partir de 0:42, pour aller directement à 1:40).
Dans la version quantique :
- il n'est pas possible de prévoir l'emplacement de la balle un instant plus tard, d'où la marche hasardeuse;
- si on superpose toutes les photographies, force est de constater qu'il y a une ou plusieurs zones où la balle ne s'y trouve jamais !
Connais-tu un objet qui fait des va-et-vient sans passer par le milieu du trajet ? Si non, la modélisation d'une particule par une boule qui se déplace "comme chez nous" n'est plus adéquate. C'est la notion même de trajectoire qui est remise en question. Quand on fait une photo, l'atome peut être modélisé par une boule pour indiqué l'emplacement détecté. Mais entre deux photos, la notion de "boule" n'a plus court, à moins d'introduire une notion de téléportation aléatoire.
Conclusion : l'atome ne se réduit pas à une boule, sauf quand on détecte sa position.
J'ai mis de côté la notion de "mode" développé dans la vidéo, que je reprendrai plus tard.
Il y a aussi une différence importante dans le monde quantique, c'est que la particule peut se trouver parfois en dehors du tube, de la zone permise par le mouvement, comme si en faisant de la balançoire l'enfant se trouvait quelque fois plus loin que la balançoire, dans les extrémités, et s'écraserait alors par terre alors qu'il ne voulait pas sauter ! Dans ces conditions, ce jeu enfantin serait depluis longtemps interdit, tout comme les pendules et les objets attachés à un ressort, les montres et les liquides dans un tube en u qui oscillent.
Comparaison d'un oscillateur classique et d'un oscillateur quantique
Je vous propose aujourd'hui un montage vidéo pour bien comprendre la différence entre notre monde habituel et le monde quantique.
Doug modélise un objet qui fait des va-et-vient (comme une balançoire, ou un objet attaché à un ressort qu'on n'a pas représenté) le long d'une droite, par une boule bleue. Son mouvement est limité vers la gauche et vers la droite. On dit que ce mouvement a un degré de liberté : il ne peut ni aller vers le haut, ni vers nous. C'est pourquoi le tube de pvc contenant la balle modélise la contrainte du mouvement.
A 0:16, la vidéo propose une suite de photographies prise à intervalle de temps régulier afin de capturer le mouvement.
Observations :
-il est facile de prévoir le lieu de la balle, l'instant suivant;
- au centre du tube la balle passe très vite;
- au bord sa vitesse diminue, jusqu'à être nulle au bord, avant de partir en sens inverse.
(Je laisse de côté la vidéo à partir de 0:42, pour aller directement à 1:40).
Dans la version quantique :
- il n'est pas possible de prévoir l'emplacement de la balle un instant plus tard, d'où la marche hasardeuse;
- si on superpose toutes les photographies, force est de constater qu'il y a une ou plusieurs zones où la balle ne s'y trouve jamais !
Connais-tu un objet qui fait des va-et-vient sans passer par le milieu du trajet ? Si non, la modélisation d'une particule par une boule qui se déplace "comme chez nous" n'est plus adéquate. C'est la notion même de trajectoire qui est remise en question. Quand on fait une photo, l'atome peut être modélisé par une boule pour indiqué l'emplacement détecté. Mais entre deux photos, la notion de "boule" n'a plus court, à moins d'introduire une notion de téléportation aléatoire.
Conclusion : l'atome ne se réduit pas à une boule, sauf quand on détecte sa position.
J'ai mis de côté la notion de "mode" développé dans la vidéo, que je reprendrai plus tard.
Il y a aussi une différence importante dans le monde quantique, c'est que la particule peut se trouver parfois en dehors du tube, de la zone permise par le mouvement, comme si en faisant de la balançoire l'enfant se trouvait quelque fois plus loin que la balançoire, dans les extrémités, et s'écraserait alors par terre alors qu'il ne voulait pas sauter ! Dans ces conditions, ce jeu enfantin serait depluis longtemps interdit, tout comme les pendules et les objets attachés à un ressort, les montres et les liquides dans un tube en u qui oscillent.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
Cas d'une particule quantique au repos
Prenons une rangée de détecteurs bien alignés et serrés, un par trait comme sur la règle ci-dessous.

Puis jetons négligemment un atome sur la règle. "Plic" dira le détecteur qui aura réagit au passage de l'atome, faisant apparaître un graphique à l'écran.

(Fonction de dirac = 0 partout sauf à l'endroit où est détectée la particule. Ici le point 0.)
Les mathématiciens ont développés des théories sur des fonctions lisses pendant 150 ans et voilà que Dirac s'en vient avec une fonction très abrupte, qui ne permet pas de prévoir le mouvement de l'atome : il a été détecté à l'endroit 0, c'est tout ce qu'on peut dire.
Si je prends un autre atome, il sera détecté peut-être en position -2.
Les chimistes ont modélisé des atomes par des petites bulles qui bougent dans tous les sens. Plus ils bougent, plus la température à notre échelle augmente. Il suffit donc de mettre un dans un endroit très très froid pour le rendre immobile, lui enlevant peu à peu son agitation, son énergie cinétique.
Dans ce cas extrême, l'atome détecté en position 0 sera quelque temps plus tard au même endroit, car immobile.
Mais pourtant, après une suite de détection, l'atome ne tient pas en place, il oscille un minimum autour de sa position de départ, de manière aléatoire. Il est où alors, puisqu'à nouveau la notion de trajectoire n'a pas cours ?

Au lieu de représenter exactement la trajectoire de l'atome oscillant, je circonscris sa zone de mouvement. L'ayant détecté au point 0, il y aura bien de la chance de le retrouver juste à côté, mais pas trop loin.
Deux manières de lire ce graphique :
1) Les traits verticaux en traits tillés indique cette chance, par rapport à une coordonnée précise notée horizontalement. Plus le segment est court, moins de chance pour l'atome de le trouver à cet endroit. Au point 0, l'atome à 0,4 = 40% de chance d'y être (c'est noté sur l'axe vertical). Au point 1, ses chances de présence se réduisent à 0,2 = 22%
2) La probabilité d'être entre 0 et 1 est de 34.1%. Pour trouver ce nombre, on calcule l'aire de la bande colorée qui nous intéresse (la bande A3 ci-dessous par exemple).

Pour calculer une zone on doit se faufiler dans les boyaux du calcul intégral:
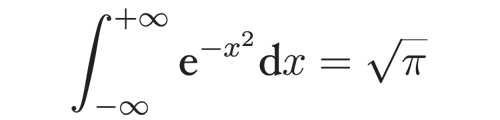 souvenirs, souvenirs ?
souvenirs, souvenirs ?
C'est le même type de courbe pour savoir où se trouve le résultat de ton test HP par rapport aux autres :

Techniquement, on veut que 2% de la population soit capable d'obtenir un 130 à ce test. Les heureux élus obtiennent un badge noté HPI. Si ton test n'es pas valide, tu n'as pas le badge mais tu peux t'appeler zèbre ou mouton.
La courbe de gauss peut être étirée vers le haut, mais alors elle doit rétrécir pour garder la même aire sous la courbe. En l'étirant à l'infini, on retombe sur la fonction de Dirac.
La conséquence de cette bougeotte est incroyable, suite au prochain numéro.
Cas d'une particule quantique au repos
Prenons une rangée de détecteurs bien alignés et serrés, un par trait comme sur la règle ci-dessous.

Puis jetons négligemment un atome sur la règle. "Plic" dira le détecteur qui aura réagit au passage de l'atome, faisant apparaître un graphique à l'écran.

(Fonction de dirac = 0 partout sauf à l'endroit où est détectée la particule. Ici le point 0.)
Les mathématiciens ont développés des théories sur des fonctions lisses pendant 150 ans et voilà que Dirac s'en vient avec une fonction très abrupte, qui ne permet pas de prévoir le mouvement de l'atome : il a été détecté à l'endroit 0, c'est tout ce qu'on peut dire.
Si je prends un autre atome, il sera détecté peut-être en position -2.
Les chimistes ont modélisé des atomes par des petites bulles qui bougent dans tous les sens. Plus ils bougent, plus la température à notre échelle augmente. Il suffit donc de mettre un dans un endroit très très froid pour le rendre immobile, lui enlevant peu à peu son agitation, son énergie cinétique.
Dans ce cas extrême, l'atome détecté en position 0 sera quelque temps plus tard au même endroit, car immobile.
Mais pourtant, après une suite de détection, l'atome ne tient pas en place, il oscille un minimum autour de sa position de départ, de manière aléatoire. Il est où alors, puisqu'à nouveau la notion de trajectoire n'a pas cours ?

Au lieu de représenter exactement la trajectoire de l'atome oscillant, je circonscris sa zone de mouvement. L'ayant détecté au point 0, il y aura bien de la chance de le retrouver juste à côté, mais pas trop loin.
Deux manières de lire ce graphique :
1) Les traits verticaux en traits tillés indique cette chance, par rapport à une coordonnée précise notée horizontalement. Plus le segment est court, moins de chance pour l'atome de le trouver à cet endroit. Au point 0, l'atome à 0,4 = 40% de chance d'y être (c'est noté sur l'axe vertical). Au point 1, ses chances de présence se réduisent à 0,2 = 22%
2) La probabilité d'être entre 0 et 1 est de 34.1%. Pour trouver ce nombre, on calcule l'aire de la bande colorée qui nous intéresse (la bande A3 ci-dessous par exemple).

Pour calculer une zone on doit se faufiler dans les boyaux du calcul intégral:
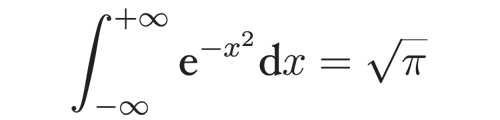 souvenirs, souvenirs ?
souvenirs, souvenirs ?C'est le même type de courbe pour savoir où se trouve le résultat de ton test HP par rapport aux autres :

Techniquement, on veut que 2% de la population soit capable d'obtenir un 130 à ce test. Les heureux élus obtiennent un badge noté HPI. Si ton test n'es pas valide, tu n'as pas le badge mais tu peux t'appeler zèbre ou mouton.
La courbe de gauss peut être étirée vers le haut, mais alors elle doit rétrécir pour garder la même aire sous la courbe. En l'étirant à l'infini, on retombe sur la fonction de Dirac.
- Spoiler:

La conséquence de cette bougeotte est incroyable, suite au prochain numéro.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
- wrong way:
- H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
Cas d'une particule quantique (au repos ou non)
Il y a une différence significative entre la courbe du test d'intelligence et celle qui indique la position d'un objet quantique.
En effet, les scores du test varient entre 0 et ... 210 pour l'instant. Le socle de la cloche est donc limité.
En revanche une particule subatomique détectée devant toi peut se trouver .... n'importe où dans l'univers un instant plus tard.
Conséquences :
a) il n'y a aucun moyen de savoir où se trouvera un électron un instant plus tard.
b) les objets quantiques vont nécessairement plus vite que la lumière, puisqu'il lui faut 8 minutes pour passer du soleil à notre terre, alors qu'un électron peut se trouver au coeur d'une étoile de la galaxie d'Andromède par exemple un milliardième de seconde plus tard.
Ratatata : Arbert a dit..."pas plus vite que la lumière."
Laissons la parole aux chercheurs Brian Cox et Jeff Forshaw sur ce sujet dans leur livre "l'univers quantique. Tout ce qui peut arriver arrive..." : "L'idée qu'une particule puisse être ici et, un instant plus tard, très loin ailleurs, n'est pas en soi en contradiction avec la théorie d'Einstein, car la limite imposée par la théorie, c'est que l'information ne peut se déplacer plus vite que la vitesse de la lumière, et la théorie quantique respecte cette contrainte. (...) le saut d'une particule n'a rien d'un transfert d'information, parce que nous ne pouvons pas savoir à l'avance où la particule va aller." (p.66)
Par exemple, le soleil envoie une lumière vers la Terre. Pour connaître sa couleur (son information), je dois attendre 8 minutes et rien dans l'univers ne peut me dire plus vite si la couleur de départ est rouge, blanche ou jaune. En criant dans la forêt, la vitesse de propagation de ma voix est celle d'une onde sonore dans notre atmosphère, qui est encore plus limitée.
En revanche, écrire un mot d'amour sur une particule et l'envoyer à notre bien-aimée n'aura pas de chance de succès dans ces conditions, car la particule n'ira pas instantanément chez ma dulcinée.
MAIS la physique quantique est l'art d'indiquer la probabilité d'apparition de la particule à un endroit donné, un instant plus tard, et non plus l'art d'indiquer la trajectoire de la particule comme en physique classique.
Mathématiquement, pour respecter le fait qu'un objet quantique puisse être instantanément partout dans l'univers, les bords de la courbe de Gauss ci-dessus ne toucheront jamais la ligne horizontale. Si l'univers est une droite, la courbe de Gauss recouvre cet univers instantanément !
Heureusement, ce chaos subatomique suit des lois de probabilités très précises qui fait qu'à notre échelle le monde est cohérent.
En résumé : un objet quantique se décrit par
a) un point (pour décrire le lieu où elle est détectée.) Dans le langage courant, on appelle ce point une particule.
b) une courbe de probabilité étalée instantanément sur l'univers entier quand elle n'est pas détectée. Cette courbe est nommée "onde" à cause des ressemblances avec les mouvements de l'eau perturbée par le jet d'une pierre.
Dans le cas d'une particule au repos, l'onde a la forme d'une courbe de Gauss.
Quand on parle de particule quantique, il faut donc penser à particlonde comme Dirac.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Je passe par ici, je ne sais pas si cette expérience a été partagée ici ( si oui, j'édite)
source:
Relais d'sciences est le centre de culture scientifique de Basse-Normandie. C'est une structure déclarée d'intérêt général dont la mission est de diffuser la culture scientifique, technique et industrielle en Basse-Normandie.
(désolée je ne peux pas poster de lien)
source:
Relais d'sciences est le centre de culture scientifique de Basse-Normandie. C'est une structure déclarée d'intérêt général dont la mission est de diffuser la culture scientifique, technique et industrielle en Basse-Normandie.
(désolée je ne peux pas poster de lien)

Ramen Taf'- Messages : 334
Date d'inscription : 16/09/2018
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Merci Ramen pour cette vidéo. Les idées sont très concises, mais les premières minutes parlent d’un effet d’objets quantiques, l’intrication, qui ne sont ni des particules ni des ondes, mais un peu des deux
C’est ce que j’essaie d’expliquer peu à peu sur ce fil.
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
Oscillateur harmonique classique, version mathématique

Reprenons l’exemple d’un objet lié par un ressort. Quand le pavé est immobile, il se trouve en position 0. Si je tire l’objet vers la droite, il se met à osciller de part et d’autre du point d’origine. Comme on imagine un mouvement sans frottement, le pavé oscillera indéfiniment entre deux valeurs fixes, -a et a. Sur le schéma la position possible du pavé est représenté par le segment rouge aa’.
Ces points dépendent :
de la masse d’objet. Plus l’objet est lourd moins la valeur a s’éloigne de la position centrale.
De la dureté du ressort. Plus il est difficile à étirer, plus l’objet oscillera près de 0. Cette dureté peut être caractérisée par un nombre positif k minuscule.
Selon qu’on étire plus ou moins le pavé, on obtiendra des valeurs différentes des positions extrêmes a et -a. Ces positions sont regroupées dans la fonction bleue V appelée potentiel, qui est la parabole 1/2 fois la dureté du ressort fois la position de l’objet au carré.
Comment utiliser ce graphique?
On tire l’objet en position -a comme sur le dessin. A ce moment l’objet est à son plus haut potentiel V(-a). Il ne pourra pas aller plus à gauche que ce point de départ. Son énergie cinétique est nulle. Son l’hamiltonien ou son énergie totale noté ici E est connu et constant : il vaut 0+V(-a).
En lâchant l’objet il va acquérir de la vitesse indiqué par K(x) sur l’image (a ne pas confondre avec le k de la dureté du ressort). A une position donnée x, E l’énergie totale du système vaudra K(x) +V(x) = E la constante de départ.
Cette équation permet de retrouver la vitesse de l’objet si on connaît sa position, ou sa position si on connaît sa vitesse. Mais en aucun cas l’énergie totale est modifiée sauf si on perturbe le système en poussant ou freinant l’objet de nos mains. Cette situation idéalisée permet alors de rajouter des frottements afin de s’approcher au mieux des cas concrets.
Voilà ce qu’il faut connaître pour aborder enfin l’oscillateur harmonique quantique !
C’est ce que j’essaie d’expliquer peu à peu sur ce fil.
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
Oscillateur harmonique classique, version mathématique

Reprenons l’exemple d’un objet lié par un ressort. Quand le pavé est immobile, il se trouve en position 0. Si je tire l’objet vers la droite, il se met à osciller de part et d’autre du point d’origine. Comme on imagine un mouvement sans frottement, le pavé oscillera indéfiniment entre deux valeurs fixes, -a et a. Sur le schéma la position possible du pavé est représenté par le segment rouge aa’.
Ces points dépendent :
de la masse d’objet. Plus l’objet est lourd moins la valeur a s’éloigne de la position centrale.
De la dureté du ressort. Plus il est difficile à étirer, plus l’objet oscillera près de 0. Cette dureté peut être caractérisée par un nombre positif k minuscule.
Selon qu’on étire plus ou moins le pavé, on obtiendra des valeurs différentes des positions extrêmes a et -a. Ces positions sont regroupées dans la fonction bleue V appelée potentiel, qui est la parabole 1/2 fois la dureté du ressort fois la position de l’objet au carré.
Comment utiliser ce graphique?
On tire l’objet en position -a comme sur le dessin. A ce moment l’objet est à son plus haut potentiel V(-a). Il ne pourra pas aller plus à gauche que ce point de départ. Son énergie cinétique est nulle. Son l’hamiltonien ou son énergie totale noté ici E est connu et constant : il vaut 0+V(-a).
En lâchant l’objet il va acquérir de la vitesse indiqué par K(x) sur l’image (a ne pas confondre avec le k de la dureté du ressort). A une position donnée x, E l’énergie totale du système vaudra K(x) +V(x) = E la constante de départ.
Cette équation permet de retrouver la vitesse de l’objet si on connaît sa position, ou sa position si on connaît sa vitesse. Mais en aucun cas l’énergie totale est modifiée sauf si on perturbe le système en poussant ou freinant l’objet de nos mains. Cette situation idéalisée permet alors de rajouter des frottements afin de s’approcher au mieux des cas concrets.
Voilà ce qu’il faut connaître pour aborder enfin l’oscillateur harmonique quantique !

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
Oscillateur harmonique quantique

1) On imagine une particule oscillant autour d'un point fixe. Plus elle a de l'énergie, plus elle peut s'éloigner de part et d'autre de ce point. Son "terrain de jeu" est limité par la courbe parabolique bleue appelée potentielle. La raideur de cette courbe s'exprime à l'aide d'un nombre, oméga, qui est analogue à la raideur k du ressort dans le cas classique.
2) L'énergie de mouvement d'une particule ne peut être nulle. Elle vaut 1,054 571 800 × 10−34 J s fois omega divisé par 2, ou symboliquement h barre fois omega/2. Ainsi un objet quantique est toujours à côté de là où il était juste avant. On a représenté la position possible théorique de la particule en E zéro sur le graphique, qui correspond à l'énergie la plus basse.

Si on donne une chiquenaude à la particule, elle passera de l'énergie E zéro à E 1, et pourra donc s'éloigner un peu plus de la position centrale. Il faut bien comprendre ce graphique, car la particule ne monte pas plus haut, comme une bonhomme sur une échelle, mais elle peut aller plus loin à sa gauche ou à sa droite, comme le pavé retenu par un ressort dans le post précédent. Son "terrain de jeu" possible est indiqué par la barre horizontale noire, selon l'énergie E de la particule.
3) Il n'y a pas d'état intermédiaire possible entre E1 et E2. En effet, on doit donner exactement la quantité d'énergie h barre fois oméga pour que son amplitude augmente. En dessous, l'objet quantique ne peut pas s'éloigner plus de sa position centrale. Concrètement on donne un bonbon de lumière (appelé quanta) d'énergie hbarre fois oméga pour augmenter l'amplitude de la particule, ou, au contraire, lorsqu'il se sépare de son bonbon, il descend son énergie d'un cran et se rapproche plus de la position centrale.
4) La probabilité de présence de l'objet quantique à un endroit choisi par l'expérimentateur dépend de son énergie totale E. Ainsi à chaque niveau d'énergie correspond une fonction d'onde psi.
La suite au prochain numéro !
Oscillateur harmonique quantique

1) On imagine une particule oscillant autour d'un point fixe. Plus elle a de l'énergie, plus elle peut s'éloigner de part et d'autre de ce point. Son "terrain de jeu" est limité par la courbe parabolique bleue appelée potentielle. La raideur de cette courbe s'exprime à l'aide d'un nombre, oméga, qui est analogue à la raideur k du ressort dans le cas classique.
2) L'énergie de mouvement d'une particule ne peut être nulle. Elle vaut 1,054 571 800 × 10−34 J s fois omega divisé par 2, ou symboliquement h barre fois omega/2. Ainsi un objet quantique est toujours à côté de là où il était juste avant. On a représenté la position possible théorique de la particule en E zéro sur le graphique, qui correspond à l'énergie la plus basse.
Si on donne une chiquenaude à la particule, elle passera de l'énergie E zéro à E 1, et pourra donc s'éloigner un peu plus de la position centrale. Il faut bien comprendre ce graphique, car la particule ne monte pas plus haut, comme une bonhomme sur une échelle, mais elle peut aller plus loin à sa gauche ou à sa droite, comme le pavé retenu par un ressort dans le post précédent. Son "terrain de jeu" possible est indiqué par la barre horizontale noire, selon l'énergie E de la particule.
3) Il n'y a pas d'état intermédiaire possible entre E1 et E2. En effet, on doit donner exactement la quantité d'énergie h barre fois oméga pour que son amplitude augmente. En dessous, l'objet quantique ne peut pas s'éloigner plus de sa position centrale. Concrètement on donne un bonbon de lumière (appelé quanta) d'énergie hbarre fois oméga pour augmenter l'amplitude de la particule, ou, au contraire, lorsqu'il se sépare de son bonbon, il descend son énergie d'un cran et se rapproche plus de la position centrale.
4) La probabilité de présence de l'objet quantique à un endroit choisi par l'expérimentateur dépend de son énergie totale E. Ainsi à chaque niveau d'énergie correspond une fonction d'onde psi.
La suite au prochain numéro !

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
@tim9.5, si un jour tu quittes Zebra, j'espère que tu laisseras ce fil entier (du moins tant que je suis là  )
)
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Encore merci tim 9.5.
Comme d'habitude, j'ai quelques questions naïves :
La courbe parabolique bleue (potentielle) représente t elle l'intégration d'un certain pourcentage de densité de probabilité fixe (90 /95 % ?). Mais donc en théorie, rien n'empêcherait l'atome de sortir de cette courbe (avec un pourcentage très faible de probabilité) ?
Je ne comprends pas très bien ce que représentent les alternances négatives des courbes pour les états d'énergie supérieurs à E0. Pour E0, la courbe représente la densité de probabilité, cf courbe de Gauss. Mais pour les états d'énergie supérieurs, une alternance négative apparaît (or on ne peut pas avoir un % de probabilité de présence négatif non ?).
Comme d'habitude, j'ai quelques questions naïves :
La courbe parabolique bleue (potentielle) représente t elle l'intégration d'un certain pourcentage de densité de probabilité fixe (90 /95 % ?). Mais donc en théorie, rien n'empêcherait l'atome de sortir de cette courbe (avec un pourcentage très faible de probabilité) ?
Je ne comprends pas très bien ce que représentent les alternances négatives des courbes pour les états d'énergie supérieurs à E0. Pour E0, la courbe représente la densité de probabilité, cf courbe de Gauss. Mais pour les états d'énergie supérieurs, une alternance négative apparaît (or on ne peut pas avoir un % de probabilité de présence négatif non ?).

REGBEL- Messages : 335
Date d'inscription : 07/03/2017
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
La probabilité de présence, c'est le carré de la fonction d'onde (en toute rigueur c'est la fonction d'onde fois son conjugué), c'est donc nécessairement positif.
La fonction d'onde est définie dans C, pas dans R, ce ne peut donc pas être une probabilité (et à vrai dire on ne peut même pas dire qu'elle est positive ou pas).
La fonction d'onde est définie dans C, pas dans R, ce ne peut donc pas être une probabilité (et à vrai dire on ne peut même pas dire qu'elle est positive ou pas).
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Merci à tous pour vos interventions !
Je vais essayer de résumer ce qu'est une particule quantique (un électron par exemple). Mais avant toute chose il faut avoir en tête le cas de... l'ornithorynque.
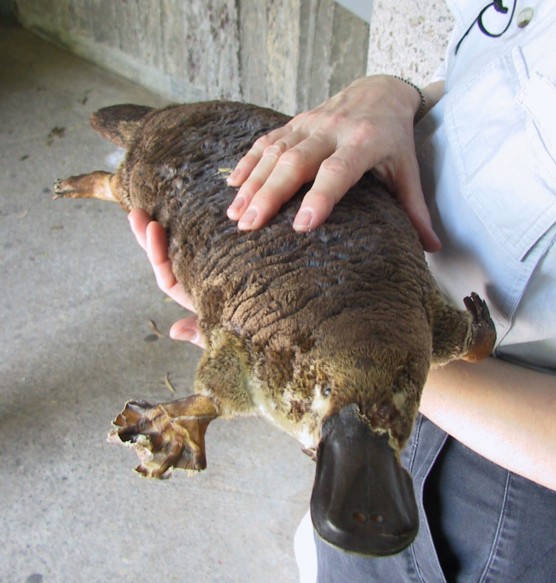
C'est un mammifère qui pond des oeufs, avec un bec de canard, une queue de castor, des pattes de loutre, les postérieurs chez les mâles possédant "un aiguillon qui peut libérer du venin capable de paralyser une jambe humaine ou même de tuer un chien." (wiki). " "Les premières années qui suivirent la découverte de l’ornithorynque, certains scientifiques européens doutèrent de son existence réelle et pensèrent qu’il s’agissait d’un canular." (wiki).
Il en est de même pour les particules quantiques qui ont l'air d'être un patchwork de notions contradictoires.
Commençons donc la non-description de l'électron.
a) Il possède un caractère corpusculaire, notamment lors de sa détection. Il se comporte alors comme une bille qui va frapper une sonnette (le détecteur) qui indiquera sa présence par un beep.
b) L'électron n'est pourtant pas une particule (cf le post du 1er septembre).
c) L'électron possède un caractère ondulatoire (cf le post du 1er octobre), qui est décrit mathématiquement par une formule nommée fonction d'onde, ou vecteur d'état (comme le spin est aussi un vecteur d'état, cf tous les posts ci-dessus de la saison 1, la mécanique quantique pour les nuls).
d) Cette fonction d'onde se comporte comme une corde qu'on secoue...
... à part qu'il n'y a pas de corde physiquement parlant.
e) Cette fonction ressemble à celle qui décrit la lumière ou les ondes acoustiques. Génial ! L'électron est une onde qui se propage en deux (ou 3) dimensions comme dans l'oscillateur harmonique, comme on pouvait le penser dans les années 1920. Deux difficultés majeures apparurent rapidement (selon Comprenons-nous vraiment la mécanique quantique. Laloë, p.25-26)
1) deux objets quantiques qui s'entrechoquent font apparaître des trajectoires bien définies qui restent bien localisées, alors que leur fonction d'onde se diffuse dans toutes les directions, "comme une onde circulaire dans une mare où une pierre a été jetée". Une description purement ondulatoire tombe dans ce cas... à l'eau !

2) Dans le cas de l'oscillateur harmonique, on considère un seul objet quantique. Mais une deuxième difficulté apparaît lorsqu'on considère un système de plusieurs objets, comme l'atome d'hydrogène (1 proton + 1 électon). La fonction d'onde qui décrit le système n'évolue plus dans un espace à 3 dimensions, mais à 3x2 dimensions. En tenant compte du spin du proton et de l'électon, "il faudrait considérer 4 ondes de ce type, qui chacune se propage dans un espace à 6 dimensions."(note p.28). On retombe en fait dans l'espace... de Hilbert connu des fidèles lecteurs de ce fil.
f) la fonction d'onde ou vecteur d'état lpsi> (sur l'image de gauche) ressemble a une densité de probabilité, mais n'en est pas une. C'est <psi l psi > (à droite) qui en est une, comme l'a rappelé hobb.

Mais quand on la représente ainsi, on perd la vision "ondulatoire comme une corde secouée". De plus, il suffit mentalement de retourner les parties de l'onde en-dessous de zéro pour obtenir à peu près la densité de droite.
e) Quand l'objet quantique est dans une des énergies définies ci-dessus (= les valeurs propres de l'hamiltonien), son vecteur d'état ne change pas dans le temps, sauf si on rajoute ou enlève de l'énergie à la particule. Ca veut dire qu'à l'endroit où la fonction d'onde traverse l'abscisse, elle a 0 probabilité d'y être. Comment donc la particule peut faire des aller-retour sans passer par ces noeuds ? Cela montre que les objets quantiques ne sont pas des particules.
f) Quand l'objet quantique est de plus en plus exité, son mouvement ressemble à un objet bien de chez nous attaché à un ressort qui fait des va-et-vient, qui passe plus de temps aux extrémités et le minimum de temps au centre .

g) Quand on lâche une balle par-terre, on sait qu'elle se trouvera forcément entre la hauteur de la main et du sol. Cette hauteur définit l'énergie potentielle de la balle, qui ne peut aller plus haut (cf poste du prof qui tente de se refaire les dents, du 31 juillet p.30). Un objet quantique peut outrepasser cette barrière si son vecteur d'état le permet (en débordant des frontières). ça signifie qu'un détecteur placé à côté de la zone tracée par le potentiel pourra réagir avec une probabilité donnée par le vecteur d'état de l'objet quantique d'une précision diabolique. Transposé à notre échelle, la balle pourrait se trouver au-dessus de ta main après l'avoir lâchée
h) quand on augmente la masse de l'objet quantique, ce phénomène disparaît peu à peu pour retomber dans le cas classique.
Résumons. L'électron n'est ni une particule ni une onde physique mais possède un caractère corpusculaire ou ondulatoire. Il peut être entièrement décrit non plus par sa position et sa vitesse comme dans le cas classique, mais par une fonction d'onde appelée vecteur d'état, qui permet de trouver la probabilité de présence de l'électon à un endroit donné.
Ce vecteur d'état n'existe pas en tant que tel dans notre espace-temps, ce n'est pas une onde physique et ce n'est pas non plus (psi carré plus précisément) une fonction mathématique de probabilité classique !
Autrement dit, ce n'est pas un outil mathématique qui varie selon les observations des physiciens, qu'on pourrait améliorer de plus en plus en augmentant les données récoltées du système observé. "En mécanique quantique standard, il est essentiel de garder à l'esprit que la fonction d'onde (ou le vecteur d'état) donne LA description ultime du système, avec toutes ses propriétés physiques; elle n'est ni contextuelle, ni dépendante de l'observateur; si elle donne des prédictions probabilistes sur les résultats de mesures futures, elle reste ainsi totalement différente d'une distribution de probabilité classique" (Delaloë p.37).
En d'autres termes, on a inventé les outils mathématiques de probabilité et de statistique classiques pour décrire des phénomènes comprenant des acteurs en trop grand nombre pour être décrit un à un, comme la répartition du test sur les HP par exemple.
Le vecteur d'état est d'une autre nature que probabiliste. "En mécanique quantique, le vecteur d'état possède un statut réellement non trivial, qui n'a aucun équivalent dans tout le reste de la physique." (ibid p.37).
Je vais essayer de résumer ce qu'est une particule quantique (un électron par exemple). Mais avant toute chose il faut avoir en tête le cas de... l'ornithorynque.

C'est un mammifère qui pond des oeufs, avec un bec de canard, une queue de castor, des pattes de loutre, les postérieurs chez les mâles possédant "un aiguillon qui peut libérer du venin capable de paralyser une jambe humaine ou même de tuer un chien." (wiki). " "Les premières années qui suivirent la découverte de l’ornithorynque, certains scientifiques européens doutèrent de son existence réelle et pensèrent qu’il s’agissait d’un canular." (wiki).
Il en est de même pour les particules quantiques qui ont l'air d'être un patchwork de notions contradictoires.
Commençons donc la non-description de l'électron.
a) Il possède un caractère corpusculaire, notamment lors de sa détection. Il se comporte alors comme une bille qui va frapper une sonnette (le détecteur) qui indiquera sa présence par un beep.
b) L'électron n'est pourtant pas une particule (cf le post du 1er septembre).
c) L'électron possède un caractère ondulatoire (cf le post du 1er octobre), qui est décrit mathématiquement par une formule nommée fonction d'onde, ou vecteur d'état (comme le spin est aussi un vecteur d'état, cf tous les posts ci-dessus de la saison 1, la mécanique quantique pour les nuls).
d) Cette fonction d'onde se comporte comme une corde qu'on secoue...
... à part qu'il n'y a pas de corde physiquement parlant.
e) Cette fonction ressemble à celle qui décrit la lumière ou les ondes acoustiques. Génial ! L'électron est une onde qui se propage en deux (ou 3) dimensions comme dans l'oscillateur harmonique, comme on pouvait le penser dans les années 1920. Deux difficultés majeures apparurent rapidement (selon Comprenons-nous vraiment la mécanique quantique. Laloë, p.25-26)
1) deux objets quantiques qui s'entrechoquent font apparaître des trajectoires bien définies qui restent bien localisées, alors que leur fonction d'onde se diffuse dans toutes les directions, "comme une onde circulaire dans une mare où une pierre a été jetée". Une description purement ondulatoire tombe dans ce cas... à l'eau !

2) Dans le cas de l'oscillateur harmonique, on considère un seul objet quantique. Mais une deuxième difficulté apparaît lorsqu'on considère un système de plusieurs objets, comme l'atome d'hydrogène (1 proton + 1 électon). La fonction d'onde qui décrit le système n'évolue plus dans un espace à 3 dimensions, mais à 3x2 dimensions. En tenant compte du spin du proton et de l'électon, "il faudrait considérer 4 ondes de ce type, qui chacune se propage dans un espace à 6 dimensions."(note p.28). On retombe en fait dans l'espace... de Hilbert connu des fidèles lecteurs de ce fil.
f) la fonction d'onde ou vecteur d'état lpsi> (sur l'image de gauche) ressemble a une densité de probabilité, mais n'en est pas une. C'est <psi l psi > (à droite) qui en est une, comme l'a rappelé hobb.

Mais quand on la représente ainsi, on perd la vision "ondulatoire comme une corde secouée". De plus, il suffit mentalement de retourner les parties de l'onde en-dessous de zéro pour obtenir à peu près la densité de droite.
e) Quand l'objet quantique est dans une des énergies définies ci-dessus (= les valeurs propres de l'hamiltonien), son vecteur d'état ne change pas dans le temps, sauf si on rajoute ou enlève de l'énergie à la particule. Ca veut dire qu'à l'endroit où la fonction d'onde traverse l'abscisse, elle a 0 probabilité d'y être. Comment donc la particule peut faire des aller-retour sans passer par ces noeuds ? Cela montre que les objets quantiques ne sont pas des particules.
f) Quand l'objet quantique est de plus en plus exité, son mouvement ressemble à un objet bien de chez nous attaché à un ressort qui fait des va-et-vient, qui passe plus de temps aux extrémités et le minimum de temps au centre .

g) Quand on lâche une balle par-terre, on sait qu'elle se trouvera forcément entre la hauteur de la main et du sol. Cette hauteur définit l'énergie potentielle de la balle, qui ne peut aller plus haut (cf poste du prof qui tente de se refaire les dents, du 31 juillet p.30). Un objet quantique peut outrepasser cette barrière si son vecteur d'état le permet (en débordant des frontières). ça signifie qu'un détecteur placé à côté de la zone tracée par le potentiel pourra réagir avec une probabilité donnée par le vecteur d'état de l'objet quantique d'une précision diabolique. Transposé à notre échelle, la balle pourrait se trouver au-dessus de ta main après l'avoir lâchée
h) quand on augmente la masse de l'objet quantique, ce phénomène disparaît peu à peu pour retomber dans le cas classique.
Résumons. L'électron n'est ni une particule ni une onde physique mais possède un caractère corpusculaire ou ondulatoire. Il peut être entièrement décrit non plus par sa position et sa vitesse comme dans le cas classique, mais par une fonction d'onde appelée vecteur d'état, qui permet de trouver la probabilité de présence de l'électon à un endroit donné.
Ce vecteur d'état n'existe pas en tant que tel dans notre espace-temps, ce n'est pas une onde physique et ce n'est pas non plus (psi carré plus précisément) une fonction mathématique de probabilité classique !
Autrement dit, ce n'est pas un outil mathématique qui varie selon les observations des physiciens, qu'on pourrait améliorer de plus en plus en augmentant les données récoltées du système observé. "En mécanique quantique standard, il est essentiel de garder à l'esprit que la fonction d'onde (ou le vecteur d'état) donne LA description ultime du système, avec toutes ses propriétés physiques; elle n'est ni contextuelle, ni dépendante de l'observateur; si elle donne des prédictions probabilistes sur les résultats de mesures futures, elle reste ainsi totalement différente d'une distribution de probabilité classique" (Delaloë p.37).
En d'autres termes, on a inventé les outils mathématiques de probabilité et de statistique classiques pour décrire des phénomènes comprenant des acteurs en trop grand nombre pour être décrit un à un, comme la répartition du test sur les HP par exemple.
Le vecteur d'état est d'une autre nature que probabiliste. "En mécanique quantique, le vecteur d'état possède un statut réellement non trivial, qui n'a aucun équivalent dans tout le reste de la physique." (ibid p.37).
- Pour aller plus loin à propos du vecteur d'état:
Autrement dit, en physique classique on mesure des propriétés intrinsèques d'un objet, sa quantité de matière par exemple (sa masse) que l'on traduit par un nombre en grammes, etc.
En physique quantique on prépare une expérience selon une procédure, (on met en relation des atomes d'argent avec un dispositif stern-gerlach comme vue dans la saison 1). "Dans cette perspective (du physicien Peres qui représente le point de vue orthodoxe), une fonction d'onde est une représentation objective (indépendante de l'observateur) d'une méthode de préparation, plutôt que du système physique lui-même. (...) Une telle définition n'exclut pas que le vecteur d'état puisse contenir de l'information sur les propriétés physiques du système." (ibid. p.38-39)
Dans l'exemple du stern-gerlach, le spineur ne comporte aucune information, sauf lorsque c'est un vecteur propre de l'opérateur. Les vecteurs propres peuvent donc être associé à des propriétés du système, dont les valeurs numériques mesurées sont leur valeur propre.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
Et nous voilà de retour avec les vecteurs d’etat lpsi>, et donc de l’espace de Hilbert, vus dans la saison 1, qu’on notait l0> ou l1> pour le système physique le plus simple en mécanique quantique, le spin de l’electron, base de l’informatique quantique et des disques durs.
Un rafraîchissement s’impose sur la notion de combinaison linéaire de vecteurs d’etats, qui a partir de deux états, permet d’en construire des milliards d’autres.
(Tu peux la visionner jusqu’a 7 Minutes, c’est suffisant pour la suite)
Et nous voilà de retour avec les vecteurs d’etat lpsi>, et donc de l’espace de Hilbert, vus dans la saison 1, qu’on notait l0> ou l1> pour le système physique le plus simple en mécanique quantique, le spin de l’electron, base de l’informatique quantique et des disques durs.
Un rafraîchissement s’impose sur la notion de combinaison linéaire de vecteurs d’etats, qui a partir de deux états, permet d’en construire des milliards d’autres.
(Tu peux la visionner jusqu’a 7 Minutes, c’est suffisant pour la suite)

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
Autre bizarrerie de la physique quantique :
 (figure H.1)
(figure H.1)
L'état ψ qui décrit entièrement la particule "coincée" dans le potentiel V, peut s'écrire sous forme de combinaisons linéaires des états ψ0, ψ1, ψ2 etc. indiqués sur l'image. Ce qui a été expliquée dans la vidéo du chat de Schrödinger pour les deux états lvivant> et lmort> peut s'appliquer pour une infinité d'états de base ψ0, ψ1, ψ2 etc.
Dans ce cas, l'énergie de l'objet quantique n'est pas définie, tant que l'on ne fait pas de mesure. Du moment que l'on fait une mesure, on obtient aléatoirement un résultat d'énergie, E4 par exemple, donc la particule sera forcément décrite par l'état ψ4. En revanche, ce qui est connu avant la mesure, c'est la probabilité d'obtenir cette énergie E4 est entièrement défini au départ dans ψ.
Autre bizarrerie de la physique quantique :
 (figure H.1)
(figure H.1)L'état ψ qui décrit entièrement la particule "coincée" dans le potentiel V, peut s'écrire sous forme de combinaisons linéaires des états ψ0, ψ1, ψ2 etc. indiqués sur l'image. Ce qui a été expliquée dans la vidéo du chat de Schrödinger pour les deux états lvivant> et lmort> peut s'appliquer pour une infinité d'états de base ψ0, ψ1, ψ2 etc.
Dans ce cas, l'énergie de l'objet quantique n'est pas définie, tant que l'on ne fait pas de mesure. Du moment que l'on fait une mesure, on obtient aléatoirement un résultat d'énergie, E4 par exemple, donc la particule sera forcément décrite par l'état ψ4. En revanche, ce qui est connu avant la mesure, c'est la probabilité d'obtenir cette énergie E4 est entièrement défini au départ dans ψ.
Dernière édition par tim9.5 le Dim 28 Oct 2018 - 19:44, édité 1 fois

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
Aujourd’hui on s’intéresse à la fonction d’onde en tant qu’une... corde à sauter.

1) Imaginons une corde à sauter qui tourne toute seule parce que l’homme est invisible. Le mouvement de la corde permet d’imaginer que le sportif se trouve sous l’endroit le plus élevé.
C’est ce qui se passe un peu en mécanique quantique. Dans le diagramme d’energie de l’oscillateur harmonique quantique posté plus haut (fig. H.1) on peut imaginer la fonction ψ0 (celle du bas) qui tourne autour de l’axe horizontal, comme une corde à sauter.
La particule invisible se trouvera probablement le plus souvent au centre, la où la corde est la plus éloignée de l’axe horizontal.
2) Quand on s’approche d’une vraie corde qui tournoie, on risque de se faire flageller. Quand on approche un détecteur d’un état ψ tournoyant on ne risque pas de toucher l’etat car il est dans le monde mathématique de Hilbert qui se superpose dans ce cas au nôtre. Ce n’est que lorsque le détecteur est placé SUR la ligne horizontale que la particule pourra être détectée avec une probabilité donnée par l’état psi.
Contrairement à la petite fille invisible, la particule peut être détectée tout près d’une poignée tournante, et non nécessairement au centre.
3) Si on regarde de profil le mouvement de la corde on observe une série de cercles de tailles différentes.

Ainsi sur chaque point où se déplace la particule on peut dessiner un cercle dont le rayon au carré nous donne la probabilité de détecter la particule à cet endroit. C’est ce qui est expliqué dans la vidéo ci-dessus des chats de Schrödinger à partir de 6:12 : un rayon de probabilité + un angle nommée la phase qui indique où se trouve la « corde à sauter » qui tourne.
4) Ainsi on peut voir les états de la fig. H.1 comme des cordes tournoyantes. Ces états sont donc différents un instant plus tard, mais le rayon d’un point de l’état qui tourne autour de l’axe horizontal ne change pas. On appelle donc ces états ψ0, ψ1, etc. des états stationnaires même s’ils bougent incessamment.
Aujourd’hui on s’intéresse à la fonction d’onde en tant qu’une... corde à sauter.

- Logobi:
- Le Logobi est un genre musical inventé en 1986 par le célèbre gangster John Pololo qui terrorisait la ville d'Abidjan par sa force physique, champion d'arts martiaux d'où il tirait son inspiration. Il fut tué en 2000 par la FIRPAC, Force d'Intervention Rapide Para-Commando, unité d'élite du président Robert Guéï dans des conditions atroces. Malgré tout, il était très populaire chez les jeunes qui l'idolâtraient. Le logobi est un style urbain né en Côte d'Ivoire. Imitant des gestes des loubards ou bandits en action lors de combats de rue, il relate les réalités sociales diverses vécues par les loubards et porte tantôt des messages de courage, tantôt des messages de loubards ou, bien plus souvent, explique la vie à travers leur vécu. Sa philosophie est basée sur la culture des arts martiaux, des réalités sociales, de la misère, et prône le courage. Le Logobi est également connu sous le nom de la « danse des gros bras » et lorsqu'il est pratiqué en acoustique ou en live, sous le nom d'« ambiance de la rue ». Wikipedia
1) Imaginons une corde à sauter qui tourne toute seule parce que l’homme est invisible. Le mouvement de la corde permet d’imaginer que le sportif se trouve sous l’endroit le plus élevé.
C’est ce qui se passe un peu en mécanique quantique. Dans le diagramme d’energie de l’oscillateur harmonique quantique posté plus haut (fig. H.1) on peut imaginer la fonction ψ0 (celle du bas) qui tourne autour de l’axe horizontal, comme une corde à sauter.
La particule invisible se trouvera probablement le plus souvent au centre, la où la corde est la plus éloignée de l’axe horizontal.
2) Quand on s’approche d’une vraie corde qui tournoie, on risque de se faire flageller. Quand on approche un détecteur d’un état ψ tournoyant on ne risque pas de toucher l’etat car il est dans le monde mathématique de Hilbert qui se superpose dans ce cas au nôtre. Ce n’est que lorsque le détecteur est placé SUR la ligne horizontale que la particule pourra être détectée avec une probabilité donnée par l’état psi.
Contrairement à la petite fille invisible, la particule peut être détectée tout près d’une poignée tournante, et non nécessairement au centre.
3) Si on regarde de profil le mouvement de la corde on observe une série de cercles de tailles différentes.

Ainsi sur chaque point où se déplace la particule on peut dessiner un cercle dont le rayon au carré nous donne la probabilité de détecter la particule à cet endroit. C’est ce qui est expliqué dans la vidéo ci-dessus des chats de Schrödinger à partir de 6:12 : un rayon de probabilité + un angle nommée la phase qui indique où se trouve la « corde à sauter » qui tourne.
4) Ainsi on peut voir les états de la fig. H.1 comme des cordes tournoyantes. Ces états sont donc différents un instant plus tard, mais le rayon d’un point de l’état qui tourne autour de l’axe horizontal ne change pas. On appelle donc ces états ψ0, ψ1, etc. des états stationnaires même s’ils bougent incessamment.
Dernière édition par tim9.5 le Dim 28 Oct 2018 - 19:53, édité 2 fois

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
.
Dernière édition par ortolan le Lun 18 Nov 2019 - 12:43, édité 1 fois

ortolan- Messages : 13579
Date d'inscription : 31/07/2016
Localisation : 404 Not Found
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Merci ortolan pour tes encouragements. Je ne pensais pas aller si loin dans la présentation de cette fascinante mécanique, mais avec internet on peut montrer des choses en général ineffables hors champ mathématique. Et en plus sur un forum on a des lecteurs à disposition, c'est génial!
Je profite de rappeler que je propose une ballade dans le monde de la mathématique quantique. Si le lecteur arrive à s'émerveiller comme dans notre enfance quand on ouvrait au hasard un livre tout plein de mystères car trop complexe pour l'âge, le but est alors atteint. Il ne devrait pas être nécessaire de lire et comprendre tous les posts précédents pour revivre cette expérience magnifique.
La vidéo suivante montre jusqu'à 5 min 38:
- l'état lpsi> qui décrit un objet quantique allant vers la droite de manière régulière, en forme de tire-bouchon.
- la mesure d'un objet en mécanique classique, puis quantique par un détecteur.
- l'effet de la mesure sur la fonction d'onde, après détection.
Je profite de rappeler que je propose une ballade dans le monde de la mathématique quantique. Si le lecteur arrive à s'émerveiller comme dans notre enfance quand on ouvrait au hasard un livre tout plein de mystères car trop complexe pour l'âge, le but est alors atteint. Il ne devrait pas être nécessaire de lire et comprendre tous les posts précédents pour revivre cette expérience magnifique.
La vidéo suivante montre jusqu'à 5 min 38:
- l'état lpsi> qui décrit un objet quantique allant vers la droite de manière régulière, en forme de tire-bouchon.
- la mesure d'un objet en mécanique classique, puis quantique par un détecteur.
- l'effet de la mesure sur la fonction d'onde, après détection.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Nous sommes désormais prêts à utiliser l'application en ligne http://www.falstad.com/qm1d/
A droite, sélectionne "setup : harmonic oscillator".
1) La parabole blanche représente le potentiel, le "terrain de jeu" possible de l'objet quantique qui se déplace horizontalement. Elle peut être modifiée par la tirette "spring constant" (la constante du ressort "attaché" à l'objet quantique).
La première ligne rouge est l'état fondamental de la particule quasi à l'arrêt.
2) Le deuxième graphique représente la probabilité d'avoir l'objet quantique sur chaque valeur de l'axe horizontal. Cette courbe déborde du potentiel, permettant à l'objet quantique d'être plus loin que permis. C'est la fonction <psi l psi> qui est en fait représenté car elle est toujours positive.
3) Le troisième graphique représente son impulsion = sa masse x sa vitesse.
4) les petites horloges représentent la phase. Dans l'état fondamental, les courbes en cloche tournent autour de l'axe horizontal. Pour représenter ce mouvement en deux dimensions, l'auteur utilise un dégradé de couleur qui traduit la valeur de l'aiguille de l'horloge. L'horloge en haut à gauche représente la phase de l'état fondamental, celle juste à droite, la phase de l'état d'énergie supérieure lpsi 1>.
En cliquant sur ces deux horloges, on crée un état intermédiaire superposé, qui est la somme de deux états, comme pour le cas des chats de Schrödinger. Dans ce cas, l'objet quantique n'a plus d'énergie définie, tant qu'on ne la mesure pas.
Résumé : en cliquant sur les lignes d'énergies horizontales, les courbes de probabilité de présence de l'objet quantique sont immobiles latéralement, tout en tournant autour de l'axe horizontal. Elles forment une base à partir de laquelle on peut écrire tout autre état de l'objet quantique, en cliquant par exemple sur les horloges ça et là.
La mécanique quantique postule que toute l'information sur le mouvement d'un objet quantique est contenu dans son vecteur d'état psi. En effet, à partir de cette courbe on obtient par un calcul automatique la courbe d'impulsion (celle juste au-dessus des horloges), grâce à la transformation de (Joseph) Fourier : qui a développé cet outil déjà en 1822.
qui a développé cet outil déjà en 1822.
Remarque : pour faire apparaître la véritable fonction d'onde lpsi>, choisis le menu "view/wave fonction/ real + imaginary part". On recouvre chaque position possible horizontale de l'objet quantique, par deux champs de nombres.
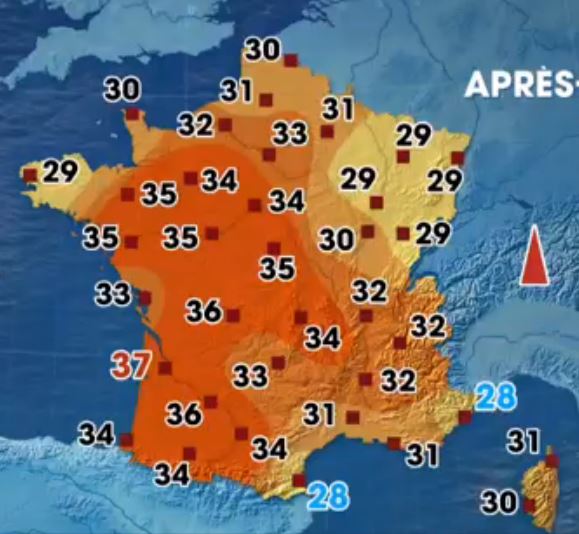
Par exemple cette carte est recouverte d'un champ scalaire de température.
Pour éviter de confondre ces deux champs superposés, on assigne un deuxième champ la lettre i. Par exemple la position centrale aura à un moment donné les nombres 4+2i. On représente ainsi le champ réel qui contient le 4 par une couleur, et le champ imaginaire contenant 2i par une autre couleur.
On tombe alors sur l'animation de wikipedia en anglais avec son commentaire : https://en.wikipedia.org/wiki/Quantum_harmonic_oscillator. A notre échelle, les objets bougent comme la balle attachée à un ressort, et dans le monde atomique les fonctions d'onde psi nous guident avant toute mesure. Une mesure même fait apparaître une particule de manière aléatoire, mais soumise aux contraintes imposées par sa fonction d'onde.
Enjoy !
A droite, sélectionne "setup : harmonic oscillator".
1) La parabole blanche représente le potentiel, le "terrain de jeu" possible de l'objet quantique qui se déplace horizontalement. Elle peut être modifiée par la tirette "spring constant" (la constante du ressort "attaché" à l'objet quantique).
La première ligne rouge est l'état fondamental de la particule quasi à l'arrêt.
2) Le deuxième graphique représente la probabilité d'avoir l'objet quantique sur chaque valeur de l'axe horizontal. Cette courbe déborde du potentiel, permettant à l'objet quantique d'être plus loin que permis. C'est la fonction <psi l psi> qui est en fait représenté car elle est toujours positive.
3) Le troisième graphique représente son impulsion = sa masse x sa vitesse.
4) les petites horloges représentent la phase. Dans l'état fondamental, les courbes en cloche tournent autour de l'axe horizontal. Pour représenter ce mouvement en deux dimensions, l'auteur utilise un dégradé de couleur qui traduit la valeur de l'aiguille de l'horloge. L'horloge en haut à gauche représente la phase de l'état fondamental, celle juste à droite, la phase de l'état d'énergie supérieure lpsi 1>.
En cliquant sur ces deux horloges, on crée un état intermédiaire superposé, qui est la somme de deux états, comme pour le cas des chats de Schrödinger. Dans ce cas, l'objet quantique n'a plus d'énergie définie, tant qu'on ne la mesure pas.
Résumé : en cliquant sur les lignes d'énergies horizontales, les courbes de probabilité de présence de l'objet quantique sont immobiles latéralement, tout en tournant autour de l'axe horizontal. Elles forment une base à partir de laquelle on peut écrire tout autre état de l'objet quantique, en cliquant par exemple sur les horloges ça et là.
La mécanique quantique postule que toute l'information sur le mouvement d'un objet quantique est contenu dans son vecteur d'état psi. En effet, à partir de cette courbe on obtient par un calcul automatique la courbe d'impulsion (celle juste au-dessus des horloges), grâce à la transformation de (Joseph) Fourier :
 qui a développé cet outil déjà en 1822.
qui a développé cet outil déjà en 1822.Remarque : pour faire apparaître la véritable fonction d'onde lpsi>, choisis le menu "view/wave fonction/ real + imaginary part". On recouvre chaque position possible horizontale de l'objet quantique, par deux champs de nombres.

Par exemple cette carte est recouverte d'un champ scalaire de température.
Pour éviter de confondre ces deux champs superposés, on assigne un deuxième champ la lettre i. Par exemple la position centrale aura à un moment donné les nombres 4+2i. On représente ainsi le champ réel qui contient le 4 par une couleur, et le champ imaginaire contenant 2i par une autre couleur.
On tombe alors sur l'animation de wikipedia en anglais avec son commentaire : https://en.wikipedia.org/wiki/Quantum_harmonic_oscillator. A notre échelle, les objets bougent comme la balle attachée à un ressort, et dans le monde atomique les fonctions d'onde psi nous guident avant toute mesure. Une mesure même fait apparaître une particule de manière aléatoire, mais soumise aux contraintes imposées par sa fonction d'onde.
Enjoy !

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies

Aujourd'hui je vous propose pour résumer l'oscillateur harmonique un jeu en ligne, qui ne fonctionne que sur ordinateur : http://learnqm.gatech.edu/WebGLtest/index.html Particle in a box qui date de 2016.
Et la version 2018, Psi and Delta : http://learnqm.gatech.edu/WebGLMay2018/index.html

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
H. Où suis-je ? Où vais-je ? Dis-le moi, hamiltonien
 (wiki deutch)
(wiki deutch)
Pour terminer, l'oscillateur harmonique quantique permet de modéliser aussi le mouvement interne d'une molécule composée de deux atomes identiques. On représente la molécule de dioxygène par exemple par deux boules d'oxygènes reliés par un ressort. Dans l'image de gauche, la longueur du ressort est exactement connue quand il est au repos. On indique alors cette valeur par un trait verticale sur l'axe bleu indiquant les valeurs possibles du ressort.
Dans le cas quantique, à droite, la longueur minimale entre deux atomes formant une molécule n'est jamais fixe, ni ne peut être égale à zéro (les atomes ne se touchent jamais). En injectant de l'énergie à la molécule, ses atomes se mettent à plus vibrer, selon des valeurs d'énergies précises, quantifiées.
 .
.
Le modèle de l'oscillateur harmonique quantique est une bonne approche pour modéliser les distances inter-nucléaires de basse énergie (les 4 premiers échelons verts). Pour un calcul plus précis, on utilise le potentiel de Morse en bleu, lui aussi quantifié. A partir d'une certaine quantité d'énergie, la molécule se dissocie et les atomes qui la caractérisaient s'éloignent à tout jamais l'un de l'autre dans un univers vide idéalisé qui ne contient que ces deux atomes. C'est ce qu'exprime l'horizontalité de la courbe bleue, à droite.
Section à suivre : zoom sur les fonctions d'onde. A moins qu'un lecteur ait une question à poser sur le chapitre H. N'hésite pas !
 (wiki deutch)
(wiki deutch)Pour terminer, l'oscillateur harmonique quantique permet de modéliser aussi le mouvement interne d'une molécule composée de deux atomes identiques. On représente la molécule de dioxygène par exemple par deux boules d'oxygènes reliés par un ressort. Dans l'image de gauche, la longueur du ressort est exactement connue quand il est au repos. On indique alors cette valeur par un trait verticale sur l'axe bleu indiquant les valeurs possibles du ressort.
Dans le cas quantique, à droite, la longueur minimale entre deux atomes formant une molécule n'est jamais fixe, ni ne peut être égale à zéro (les atomes ne se touchent jamais). En injectant de l'énergie à la molécule, ses atomes se mettent à plus vibrer, selon des valeurs d'énergies précises, quantifiées.
 .
.Le modèle de l'oscillateur harmonique quantique est une bonne approche pour modéliser les distances inter-nucléaires de basse énergie (les 4 premiers échelons verts). Pour un calcul plus précis, on utilise le potentiel de Morse en bleu, lui aussi quantifié. A partir d'une certaine quantité d'énergie, la molécule se dissocie et les atomes qui la caractérisaient s'éloignent à tout jamais l'un de l'autre dans un univers vide idéalisé qui ne contient que ces deux atomes. C'est ce qu'exprime l'horizontalité de la courbe bleue, à droite.
Section à suivre : zoom sur les fonctions d'onde. A moins qu'un lecteur ait une question à poser sur le chapitre H. N'hésite pas !

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
I. La fonction d'onde
a) Une vague peut être modélisé par des êtres humains alignés qui restent sur place, tout en modifiant leur hauteur (dans la vidéo ils se courbent). Ce qu'il faut retenir :
1) c'est qu'ils ne se déplacent pas vers la droite, contrairement à l'impression que donne la vague quand on la regarde
2) ils se déplacent en fait dans une seule direction, puis reviennent à leur place. https://www.geogebra.org/m/dwyw6zah
On peut mieux le voir dans la vidéo suivante qui modélise la transmission du son.
Dans l'espace, il n'y a pas de molécule d'air, donc pas de déplacement de molécule, donc pas d'onde sonore.
b) la lumière peut être vue comme une vague, une onde qui se propage dans l'éther qui remplit l'univers. A part que les molécules d'ether n'existent pas, ce qui prit plusieurs siècles pour le prouver. On a donc des ondes qui se déplacent sans support, dans le vide entre le soleil et la terre. On les décrit comme des variations de champ électrique et magnétique perpendiculaire entre eux qui se déplacent. https://www.geogebra.org/m/xhYwXSsH C'est en fait un modèle mathématique bien pratique. Pourtant on ne sait pas et on ne peut pas savoir quelle est la nature, la "forme" de cette onde (je cite wikipedia "photon dualité onde-corpuscule") car pour la connaître il faut interagir avec elle, et lorsqu'on interagit avec la lumière, elle se présente sous forme granuleuse uniquement. La lumière est aussi un objet quantique !
Electrons et lumière sont pareils de ce côté-là : modélisables par des ondes quand on ne détecte pas, et par des particules lors d'interactions inévitables pour les mesurer.
Une excellente vidéo d'introduction aux ondes liées aux objets quantiques :
a) jusqu'à 2 min 40 : présentation d'une onde quantique;
b) jusqu'à 3 min 40 : comparaison de deux ondes quantiques;
c) jusqu'à 4 min 55: rajout d'un potentiel V qui modifie la trajectoire de l'onde; (la suite de la vidéo sera commentée dans un poste ultérieur).
d) fréquence et transformée de Fourier : une onde (sonore par exemple https://academo.org/demos/spectrum-analyzer/) peut toujours être décomposée en ondes plus régulières, comme dans l'image ci-dessous. En effet, l'onde rouge peut s'écrire comme l'addition des trois autres ondes sinusoïdales. La fréquence n'est autre que le nombre de répétitions du motif complet en une seconde qui se cache dans l'onde. Elle se mesure en Herz pour les ondes sonores. La note de musique "la" est donc une onde qui comporte 440 vaguelettes d'air qui atteindront mon oreille pendant 1 seconde. http://www.physics-chemistry-interactive-flash-animation.com/electricity_electromagnetism_interactive/oscilloscope_description_tutorial_sounds_frequency.htm
La transformée de Fournier n'est donc qu'une astuce mathématique qui consiste à regarder une onde de profil en tournant la tête de 90°.
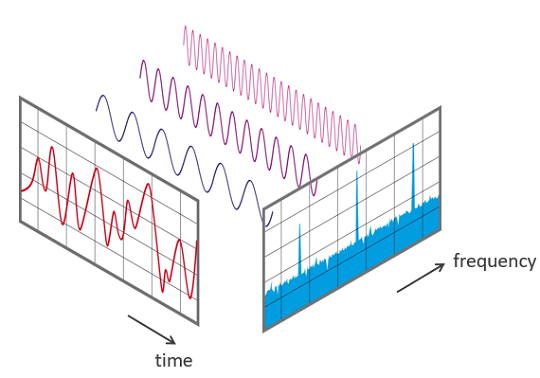
D'autres exemples d'onde "vues de face", à gauche (l'axe horizontal décrivant le temps), et de "profil" selon la fréquence.
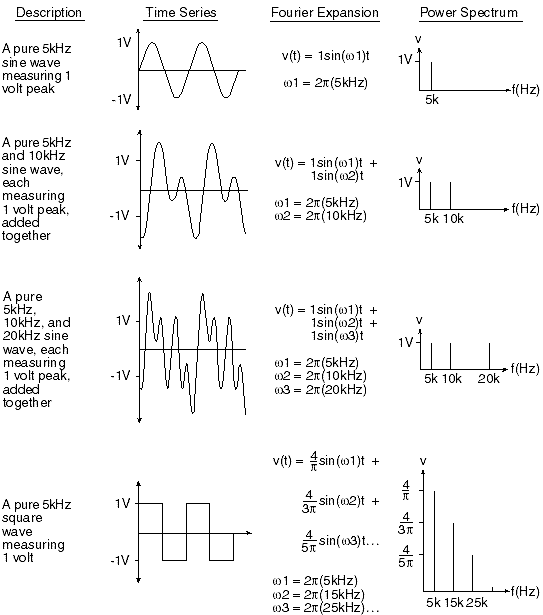
On trouve même des calculatrices en ligne : https://sooeet.com/math/online-fft-calculator.php
- choisis dans "user data exemples" un saxophone par exemple, puis appuie sur "play". La calculatrice te donne le son du saxo décomposé en fréquences. En appuyant sur "Inv-Ftt", tu obtiens le graphique de la durée du son.
Pour terminer, amuse-toi en additionnant deux ondes de couleurs pour obtenir la courbe sombre : https://www.geogebra.org/m/kMYRHveA
a) Une vague peut être modélisé par des êtres humains alignés qui restent sur place, tout en modifiant leur hauteur (dans la vidéo ils se courbent). Ce qu'il faut retenir :
1) c'est qu'ils ne se déplacent pas vers la droite, contrairement à l'impression que donne la vague quand on la regarde
2) ils se déplacent en fait dans une seule direction, puis reviennent à leur place. https://www.geogebra.org/m/dwyw6zah
On peut mieux le voir dans la vidéo suivante qui modélise la transmission du son.
Dans l'espace, il n'y a pas de molécule d'air, donc pas de déplacement de molécule, donc pas d'onde sonore.
b) la lumière peut être vue comme une vague, une onde qui se propage dans l'éther qui remplit l'univers. A part que les molécules d'ether n'existent pas, ce qui prit plusieurs siècles pour le prouver. On a donc des ondes qui se déplacent sans support, dans le vide entre le soleil et la terre. On les décrit comme des variations de champ électrique et magnétique perpendiculaire entre eux qui se déplacent. https://www.geogebra.org/m/xhYwXSsH C'est en fait un modèle mathématique bien pratique. Pourtant on ne sait pas et on ne peut pas savoir quelle est la nature, la "forme" de cette onde (je cite wikipedia "photon dualité onde-corpuscule") car pour la connaître il faut interagir avec elle, et lorsqu'on interagit avec la lumière, elle se présente sous forme granuleuse uniquement. La lumière est aussi un objet quantique !
- Photon (extrait de wiki):
- Ainsi, l’onde électromagnétique, c’est-à-dire la valeur du champ électrique et du champ magnétique en fonction de l’endroit et du moment a donc deux significations :
a) macroscopique : lorsque le flux d’énergie est suffisamment important, ce sont les champs électrique et magnétique mesurés par un appareil macroscopique (par exemple antenne réceptrice, un électroscope ou une sonde de Hall) ;
b) microscopique : elle représente la probabilité de présence des photons, c’est-à-dire la probabilité qu’en un endroit donné il y ait une interaction quantifiée (c’est-à-dire d’une énergie hν déterminée).
Electrons et lumière sont pareils de ce côté-là : modélisables par des ondes quand on ne détecte pas, et par des particules lors d'interactions inévitables pour les mesurer.
Une excellente vidéo d'introduction aux ondes liées aux objets quantiques :
a) jusqu'à 2 min 40 : présentation d'une onde quantique;
b) jusqu'à 3 min 40 : comparaison de deux ondes quantiques;
c) jusqu'à 4 min 55: rajout d'un potentiel V qui modifie la trajectoire de l'onde; (la suite de la vidéo sera commentée dans un poste ultérieur).
d) fréquence et transformée de Fourier : une onde (sonore par exemple https://academo.org/demos/spectrum-analyzer/) peut toujours être décomposée en ondes plus régulières, comme dans l'image ci-dessous. En effet, l'onde rouge peut s'écrire comme l'addition des trois autres ondes sinusoïdales. La fréquence n'est autre que le nombre de répétitions du motif complet en une seconde qui se cache dans l'onde. Elle se mesure en Herz pour les ondes sonores. La note de musique "la" est donc une onde qui comporte 440 vaguelettes d'air qui atteindront mon oreille pendant 1 seconde. http://www.physics-chemistry-interactive-flash-animation.com/electricity_electromagnetism_interactive/oscilloscope_description_tutorial_sounds_frequency.htm
La transformée de Fournier n'est donc qu'une astuce mathématique qui consiste à regarder une onde de profil en tournant la tête de 90°.

D'autres exemples d'onde "vues de face", à gauche (l'axe horizontal décrivant le temps), et de "profil" selon la fréquence.

On trouve même des calculatrices en ligne : https://sooeet.com/math/online-fft-calculator.php
- choisis dans "user data exemples" un saxophone par exemple, puis appuie sur "play". La calculatrice te donne le son du saxo décomposé en fréquences. En appuyant sur "Inv-Ftt", tu obtiens le graphique de la durée du son.
Pour terminer, amuse-toi en additionnant deux ondes de couleurs pour obtenir la courbe sombre : https://www.geogebra.org/m/kMYRHveA

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Y'a pas de quoi, ludion !
I.2 La fonction d'onde et le principe d'indétermination
a) Nous avons vu qu'on peut additionner des ondes simples, de forme sinusoïdale, pour obtenir une onde plus compliquée, et vice-versa, comme le montre l'animation wiki

b) La transformée de Fourier permet de passer d'une description de la particule selon sa position à une description de sa vitesse (sa fréquence, ou son impulsion = sa masse x sa vitesse).
c) L'onde décrivant la vitesse (en vert) est "inversement proportionnelle" à l'onde décrivant la position (en rouge).

Plus la position de l'objet quantique est précisé (onde rouge se resserrant), plus sa vitesse prend toute sorte de valeur (onde verte s'étalant).
Le "triangle x" se lit "delta x", delta étant une lettre grecque en forme de triangle. Si la particule se trouve en x0 = 4, alors sa vitesse k pourra prendre toute sorte de valeur. Si l'onde est plus ou moins contenue dans un intervalle delta x (comme en (b) sur l'image), sa vitesse pourra varier d'un certain nombre delta k.
d) Il y a un lien précis entre l'étalement delta x et l'étalement delta k, qui se nomme "relation d'indétermination", décrite par Heisenberg il y a bientôt 100 ans, mais qui a pris historiquement le nom de "relation d'incertitude". Ce lien signifie qu'on peut trouver précisément la position d'une particule, mais c'est au détriment de sa vitesse, et réciproquement.
Autrement dit, delta x et delta k sont les côtés d'un rectangle qui ne peut jamais être réduit à un segment. Plus précisément, l'aire de ce rectangle vaut presque 0 mais pas 0, c'est-à-dire 0.00000000000000000000000000000000005272859 J s (Joule seconde) !
Par souci de commodité, ce nombre s'écrit h barre divisé par 2, le h n'étant pas la hauteur du rectangle mais la constante universelle de Planck qui définit depuis deux semaines la valeur du kilogramme ! (Vidéode propagande sur https://www.kaltura.com/index.php/extwidget/preview/partner_id/684682/uiconf_id/43329031/entry_id/1_2qyyvd0q/embed/dynamic? avec l'explication brève du fonctionnement de la balance de Watt qui mesure cette constante h en pdf https://www.metas.ch/dam/data/metas/Dokumentation/METASPublikationen/metinfo/METinfo2016/Comment%20la%20balance%20du%20watt%20fonctionne.pdf)
Ce rectangle "d'indétermination" est visualisé sur une vidéo déjà "entamée", à partir de 6:19, et plus précisément à partir de 10 minutes :

Lorsque l'aire de ce rectangle est nulle, on est face à des objets décrits par la mécanique classique. Lorsque l'aire vaut h barre demi, les maths quantiques doivent être utilisées. Il existe un domaine de recherche qui s'intéresse au passage quantique-classique nommé décohérence.
I.2 La fonction d'onde et le principe d'indétermination
a) Nous avons vu qu'on peut additionner des ondes simples, de forme sinusoïdale, pour obtenir une onde plus compliquée, et vice-versa, comme le montre l'animation wiki

b) La transformée de Fourier permet de passer d'une description de la particule selon sa position à une description de sa vitesse (sa fréquence, ou son impulsion = sa masse x sa vitesse).
c) L'onde décrivant la vitesse (en vert) est "inversement proportionnelle" à l'onde décrivant la position (en rouge).

Plus la position de l'objet quantique est précisé (onde rouge se resserrant), plus sa vitesse prend toute sorte de valeur (onde verte s'étalant).
Le "triangle x" se lit "delta x", delta étant une lettre grecque en forme de triangle. Si la particule se trouve en x0 = 4, alors sa vitesse k pourra prendre toute sorte de valeur. Si l'onde est plus ou moins contenue dans un intervalle delta x (comme en (b) sur l'image), sa vitesse pourra varier d'un certain nombre delta k.
d) Il y a un lien précis entre l'étalement delta x et l'étalement delta k, qui se nomme "relation d'indétermination", décrite par Heisenberg il y a bientôt 100 ans, mais qui a pris historiquement le nom de "relation d'incertitude". Ce lien signifie qu'on peut trouver précisément la position d'une particule, mais c'est au détriment de sa vitesse, et réciproquement.
Autrement dit, delta x et delta k sont les côtés d'un rectangle qui ne peut jamais être réduit à un segment. Plus précisément, l'aire de ce rectangle vaut presque 0 mais pas 0, c'est-à-dire 0.00000000000000000000000000000000005272859 J s (Joule seconde) !
Par souci de commodité, ce nombre s'écrit h barre divisé par 2, le h n'étant pas la hauteur du rectangle mais la constante universelle de Planck qui définit depuis deux semaines la valeur du kilogramme ! (Vidéo
Ce rectangle "d'indétermination" est visualisé sur une vidéo déjà "entamée", à partir de 6:19, et plus précisément à partir de 10 minutes :
Lorsque l'aire de ce rectangle est nulle, on est face à des objets décrits par la mécanique classique. Lorsque l'aire vaut h barre demi, les maths quantiques doivent être utilisées. Il existe un domaine de recherche qui s'intéresse au passage quantique-classique nommé décohérence.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
I.2 Le principe d'indétermination
Dans cette vidéo, les photons émis par un laser passent en ligne droite à travers une fente.
A un certain moment, plus on diminue la fente (delta x) par laquelle passe les photons, plus leur vitesse (delta p) change de direction. Le principe énoncé par Heisenberg se voit donc aussi à notre échelle.
Dans cette vidéo, les photons émis par un laser passent en ligne droite à travers une fente.
A un certain moment, plus on diminue la fente (delta x) par laquelle passe les photons, plus leur vitesse (delta p) change de direction. Le principe énoncé par Heisenberg se voit donc aussi à notre échelle.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
I.2 Le principe d'indétermination avec des électrons (partie 1)
Historiquement, les électrons ont d'abord été découverts en tant que corpuscules (grâce aux tubes de Crookes) représentant une quantité indivisible de charge électrique (cf Richard Laming.)
En faisant passer des billes de paintball à travers une fente vers un écran (optical screen), on obtient plutôt une tache selon la forme du trou:

De même pour un faisceau d'électrons.
En revanche, pour une fente très très fine, les électrons s'étalent au lieu d'aller tout droit, en tenant compte de la relation d'Heisenberg et donc de la variation possible de la direction de la vitesse de l'électron.
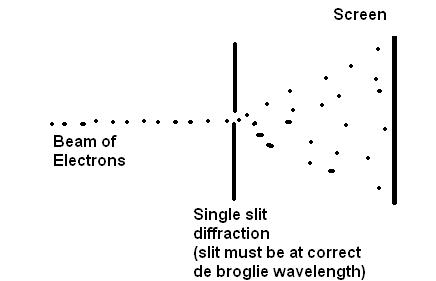
En mettant des lignes de guidage, ça donne

Sur l'écran vu de face, on obtient le motif suivant à partir d'une fente circulaire :
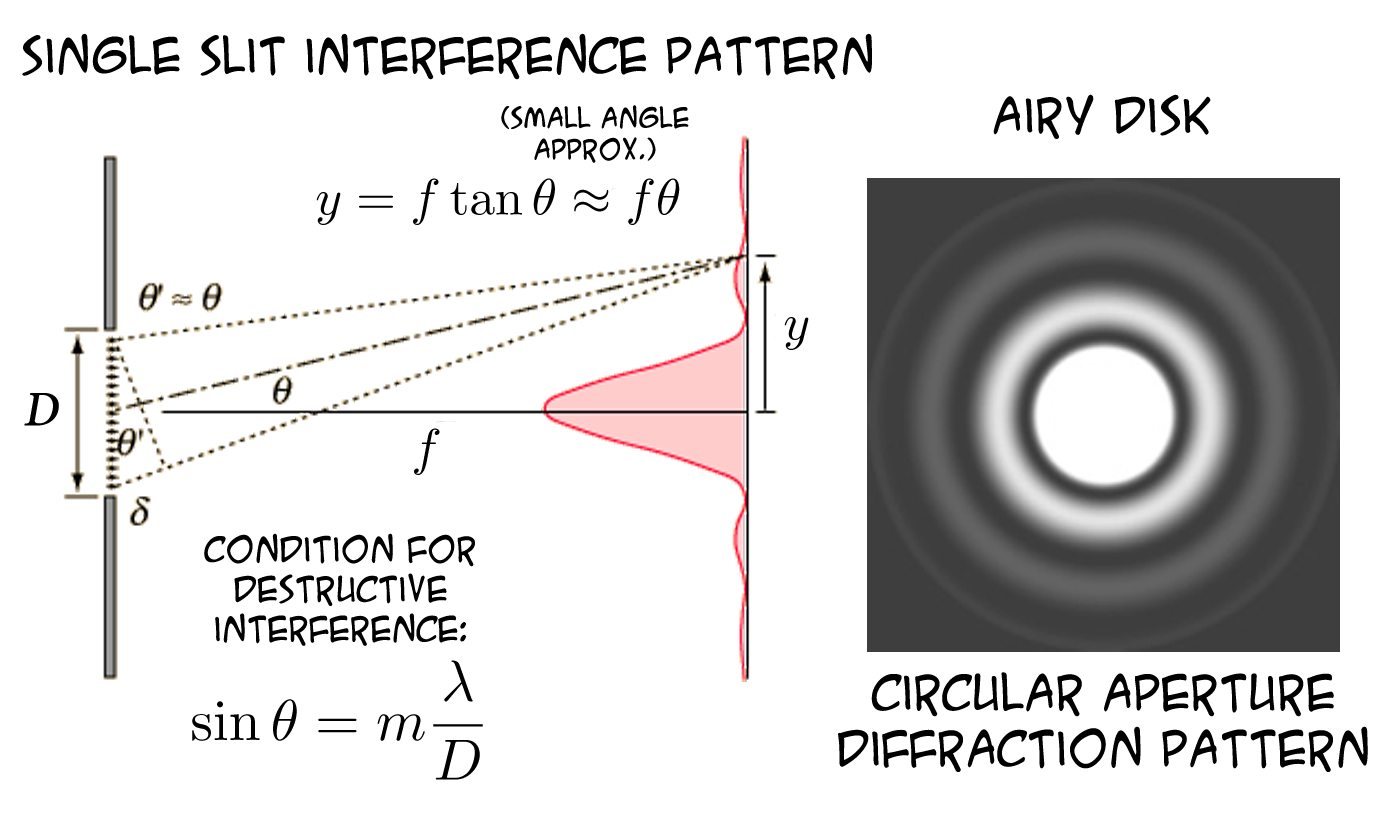
Beaucoup d'impact au centre, puis sur des anneaux de moins en moins marqué. En plus, entre les anneaux, tout est sombre. Ca signifie que les électrons-particules ne s'écrasent jamais dans cette région ! Expérience impossible à réaliser avec des billes de paintball passant par une fente.
Mais on obtient le même résultat que si on projetait un rayon-X (qui est une onde), à travers la fente. A gauche, la version rayons X, à droite celle les électrons.

Historiquement, les électrons ont d'abord été découverts en tant que corpuscules (grâce aux tubes de Crookes) représentant une quantité indivisible de charge électrique (cf Richard Laming.)
En faisant passer des billes de paintball à travers une fente vers un écran (optical screen), on obtient plutôt une tache selon la forme du trou:

De même pour un faisceau d'électrons.
En revanche, pour une fente très très fine, les électrons s'étalent au lieu d'aller tout droit, en tenant compte de la relation d'Heisenberg et donc de la variation possible de la direction de la vitesse de l'électron.
En mettant des lignes de guidage, ça donne

Sur l'écran vu de face, on obtient le motif suivant à partir d'une fente circulaire :

Beaucoup d'impact au centre, puis sur des anneaux de moins en moins marqué. En plus, entre les anneaux, tout est sombre. Ca signifie que les électrons-particules ne s'écrasent jamais dans cette région ! Expérience impossible à réaliser avec des billes de paintball passant par une fente.

Mais on obtient le même résultat que si on projetait un rayon-X (qui est une onde), à travers la fente. A gauche, la version rayons X, à droite celle les électrons.


tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Zoom sur les ondes en général
Toute une théorie a déjà été développée sur les ondes avant la mécanique quantique. Pour visualiser une onde, l'exemple d'une surface de l'eau perturbée par une goutte d'eau est parfait.

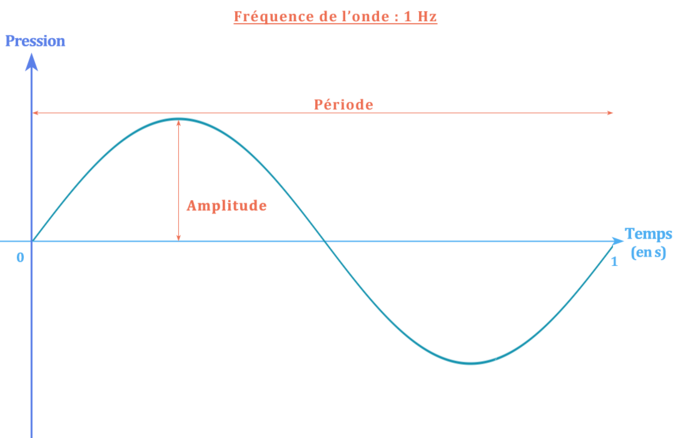
On choisit un point sur l'image de droite, par exemple, le lieu de l'impact de la goutte avec la surface. Et on regarde la hauteur de l'eau à cet endroit. A zéro seconde, l'eau est au niveau 0 à l'endroit choisi. Un quart de seconde plus tard, l'eau est à sa hauteur maximum, tandis qu'à 3/4 de sec elle est à son minimum. Finalement, au temps t= 1 sec, l'eau retrouve sa position initiale. Dans un cas idéalisé, ce mouvement se répète indéfiniment chaque seconde.
Mathématiquement, une telle onde se modélise par la fonction sinus (ou cosinus) qui contient les paramètres suivants :
- l'amplitude a = la hauteur maximale de la vague.
- la fréquence f = le nombre d'oscillations répétées durant une seconde.
- la phase ɸ phi qui indique le décalage de l'onde à l'origine quand t=0, ou en d'autres termes, à quelle hauteur se trouve la vague au temps t = 0. (ici, ɸ = 0).
La fonction qui modélise l'onde en fonction du temps t s'écrit y(t) = a fois sin(2 fois pi fois f fois t + phi).
Grâce à Madame Geneviève, nous pouvons visualiser facilement cette fonction paramétrable : http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Ondes/general/sinus.php. Notons que l'axe du temps horizontal se mesure en ms.
Une analogie : le rebond sur un trampoline (jusqu'à 0:40).
Il est en général interdit d'être deux sur un trampoline, à cause des différentes phases générées par chaque enfant :
- quand les enfants sont en phase, ils sautent beaucoup plus haut que tout seul. Si l'un des deux est plus léger que l'autre, il est parfois éjecté du trampoline.
- quand les enfants sont en phase opposées, leurs mouvements s'annulent et le trampoline devient immobile comme un sol normal.
La simulation suivante permet de bien comprendre le rôle des phases : http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Ondes/general/somme.php
La courbe bleue + la courbe rouge donne la courbe verte. Si les phases sont opposées, la courbe verte est plate.
Version avec multi courbes : http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Ondes/general/synthese.php. Dans la simulation, déplacer quelques carrés vers le haut.
C'est ainsi que fonctionnent les casques réducteurs de bruit. Ils détectent la fréquence du son qui entre dans l'oreille et envoie la même onde, mais déphasée, pour qu'elles se détruisent mutuellement au niveau du tympan. Comme les sons sont complexes, il faut d'abord les décomposer cen temps réels comme vu dans le poste plus haut, ce qui demande une miniaturisation du processeur qui fait ce boulot.
La n°18 par exemple.
Toute une théorie a déjà été développée sur les ondes avant la mécanique quantique. Pour visualiser une onde, l'exemple d'une surface de l'eau perturbée par une goutte d'eau est parfait.

On choisit un point sur l'image de droite, par exemple, le lieu de l'impact de la goutte avec la surface. Et on regarde la hauteur de l'eau à cet endroit. A zéro seconde, l'eau est au niveau 0 à l'endroit choisi. Un quart de seconde plus tard, l'eau est à sa hauteur maximum, tandis qu'à 3/4 de sec elle est à son minimum. Finalement, au temps t= 1 sec, l'eau retrouve sa position initiale. Dans un cas idéalisé, ce mouvement se répète indéfiniment chaque seconde.
Mathématiquement, une telle onde se modélise par la fonction sinus (ou cosinus) qui contient les paramètres suivants :
- l'amplitude a = la hauteur maximale de la vague.
- la fréquence f = le nombre d'oscillations répétées durant une seconde.
- la phase ɸ phi qui indique le décalage de l'onde à l'origine quand t=0, ou en d'autres termes, à quelle hauteur se trouve la vague au temps t = 0. (ici, ɸ = 0).
La fonction qui modélise l'onde en fonction du temps t s'écrit y(t) = a fois sin(2 fois pi fois f fois t + phi).
Grâce à Madame Geneviève, nous pouvons visualiser facilement cette fonction paramétrable : http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Ondes/general/sinus.php. Notons que l'axe du temps horizontal se mesure en ms.
Une analogie : le rebond sur un trampoline (jusqu'à 0:40).
Il est en général interdit d'être deux sur un trampoline, à cause des différentes phases générées par chaque enfant :
- quand les enfants sont en phase, ils sautent beaucoup plus haut que tout seul. Si l'un des deux est plus léger que l'autre, il est parfois éjecté du trampoline.
- quand les enfants sont en phase opposées, leurs mouvements s'annulent et le trampoline devient immobile comme un sol normal.
La simulation suivante permet de bien comprendre le rôle des phases : http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Ondes/general/somme.php
La courbe bleue + la courbe rouge donne la courbe verte. Si les phases sont opposées, la courbe verte est plate.
Version avec multi courbes : http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Ondes/general/synthese.php. Dans la simulation, déplacer quelques carrés vers le haut.
C'est ainsi que fonctionnent les casques réducteurs de bruit. Ils détectent la fréquence du son qui entre dans l'oreille et envoie la même onde, mais déphasée, pour qu'elles se détruisent mutuellement au niveau du tympan. Comme les sons sont complexes, il faut d'abord les décomposer cen temps réels comme vu dans le poste plus haut, ce qui demande une miniaturisation du processeur qui fait ce boulot.
La n°18 par exemple.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Encartade :
Quand deux boules de billard s'entrechoquent, on obtient ceci :
avec un point de contact bien précis.
Quand deux objets quantiques s'élancent l'un contre l'autre, ils échangent leur position sans se toucher ! Arrives-tu à concevoir cela ?
La vidéo suivante propose de décrire ces deux objets (deux électrons par exemple), par leur onde de probabilité de se trouver à tel endroit.
Effectivement, les deux ondes s'échangent sans partager un espace commun. (C'est le titre de la vidéo).
NB : les vidéos des mouvements A et B représente la 2D. Tout est plat ! L'un ne peut sauter par-dessus l'autre. Incroyable n'est-ce pas?
A 1min19: on montre la solution pour deux vaguelettes "normales" à notre échelle, à 2min36 la simulation pour deux ondes quantiques.
Le mouvement est très lent car refroidi à une température plus basse que le vide interstellaire.
A quoi peut servir cette recherche fondamentale ? : à améliorer la résolution des microscopes car plus on zoome, plus des effets quantiques étranges apparaissent.
Quand deux boules de billard s'entrechoquent, on obtient ceci :

avec un point de contact bien précis.
Quand deux objets quantiques s'élancent l'un contre l'autre, ils échangent leur position sans se toucher ! Arrives-tu à concevoir cela ?
La vidéo suivante propose de décrire ces deux objets (deux électrons par exemple), par leur onde de probabilité de se trouver à tel endroit.
Effectivement, les deux ondes s'échangent sans partager un espace commun. (C'est le titre de la vidéo).
NB : les vidéos des mouvements A et B représente la 2D. Tout est plat ! L'un ne peut sauter par-dessus l'autre. Incroyable n'est-ce pas?
A 1min19: on montre la solution pour deux vaguelettes "normales" à notre échelle, à 2min36 la simulation pour deux ondes quantiques.
Le mouvement est très lent car refroidi à une température plus basse que le vide interstellaire.
A quoi peut servir cette recherche fondamentale ? : à améliorer la résolution des microscopes car plus on zoome, plus des effets quantiques étranges apparaissent.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
J'aimerais remercier tim9.5 et les autres  qui contribuent a ce fil que je lis avec attention
qui contribuent a ce fil que je lis avec attention  , je suis rendu seulement à la page 10
, je suis rendu seulement à la page 10  , mais j'avance progressivement.
, mais j'avance progressivement. 
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Sacré boulot et belle démarche en effet que celle de tim9.5 ! Cependant je dois avouer avoir un profond doute sur la vidéo illustrant le "principe d'incertitude d'Heisenberg" ; clairement je ne vois pas en quoi il est utile ici pour expliquer le phénomène observé, la diffraction classique (en régime de Fraunhofer) étant -pour moi- largement suffisante. En fait je pense que beaucoup de vulgarisateurs tombent dans ce piège de vouloir faire dire à ce principe un peu tout et n'importe quoi...
jaravan- Messages : 26
Date d'inscription : 01/08/2017
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Merci pour vos encouragements ! Si tu as des questions, ô "champ de l'abstraction", n'hésite pas à les poser, en citant aussi le texte et la page du fil en question, qui s'allonge, qui s'allonge.
Jaravan, ta remarque est pertinente : l'optique est joyau poli pendant des siècles pour arriver à être capable de décrire la trajectoire d'un rayon lumineux à travers des lentilles, des fentes, etc.
Pour ma part, je part du constat suivant : un phénomène physique peut très souvent être plus ou moins bien être décrit par différents modèles : dans le cas de l'optique, le rayon lumineux peut être représenté par une droite toute droite, comme dans la harpe de JM Jarre :
Ou par un ensemble de points dont chaque point se transforme en cercle qui grandit, cercle fait de points qui à leur tour se transforme en cercles, répétés à l'infini :
Cet artifice mathématique est intéressant surtout lorsque la lumière rencontre un obstacle (comme en 2min35), ou un trou.
Pour faire court, la lumière, l'eau, le son, même un pet dans la nature s'expliquent mathématiquement avec ce principe. En poussant plus loin, on passe par Fraunhofer.
Comme en math on aime bien utiliser un nouvel outil sur toutes sortes d'expériences déjà résolues, on arrive à appliquer la transformée de Fourier en diffraction classique. Tant que ça simplifie les calculs, pourquoi pas ?
https://lob.epfl.ch/webdav/site/lob/users/113390/public/P1%20Fourier%20optics.pdf
Au lieu de travailler avec des nombres réels, on évite les sin et les cos en réécrivant une onde à l'aide des nombres complexes (le fameux i= racine de -1).
 . Et en plus les réactions des ondes peuvent s'expliquer par <psi l psi>, (psi au carré) ! Tiens, on s'approche dangereusement des états lpsi> quantiques !
. Et en plus les réactions des ondes peuvent s'expliquer par <psi l psi>, (psi au carré) ! Tiens, on s'approche dangereusement des états lpsi> quantiques !
Puis Einstein, dit : l'effet photoélectrique (c'est-à-dire transformer de l'énergie lumineuse en énergie électrique) s'explique quand on modélise cet échange par des paquets d'énergie (des quantas), des boules quoi. En d'autres termes il dit que les vagues de l'océan (les ondes lumineuses) doivent être en forme de rocher (les quantas) quand elles buttent sur la berge métallique, pour que celle-ci recrache un morceau d'électricité (l'électron). Allô la Terre !

Plus tard, le Français de Broglie affirme la réciproque : si Einstein associe un paquet d'énergie (un caillou) à une onde lumineuse, pourquoi ne pas associer, une onde à chaque élément de matière (un électron-caillou par exemple) ?
En résumé : les cailloux qui passent à travers la fente unique se comportent comme un pet à travers la fente ! (ou, pour être précis dans le cas de de Broglie, suivent une trajectoire dictée par un vent mystérieux, non-détectable lui-même mais bien réel car ce vent fait dévier les cailloux).
Et c'est là qu'intervient le fameux h de Planck. C'est ce nombre qui fait le passage entre le monde des ondes, et le monde des particules. Effectivement les modèles classiques prédisent correctement les réactions d'une onde passant par une fente, mais la mécanique quantique - par son formalisme mathématique dual (onde-corpuscule) - décrivent non seulement ces phénomènes classiques, mais permirent la construction d'un microscope électronique, où la lumière utilisée dans un microscope optique qui traverse l'échantillon pour le révéler à nos yeux, est remplacée par un faisceau d'électrons, dont la longueur d'onde est plus petite. Par conséquent les électrons révèlent bien plus de détails, ce qui permet de zoomer plus loin. Et tout cela car on tient compte de cette dualité. De manière élégante dans la relation d'Heisenberg.
Pour aller plus loin : une expérience de salon proposé par un constructeur officiel :
https://www.phywe.com/en/diffraction-at-a-slit-and-heisenberg-s-uncertainty-principle.html#tabs1 Voir le mode d'emploi pour plus de détail.
D'autres commentaires : https://physics.stackexchange.com/questions/114227/interesting-relationship-between-diffraction-and-heisenbergs-uncertainty-princi
d'où est tirée la conclusion suivante :
"All in all, HUP considers the particle nature of light while Huygens' principle considers the wave nature of light." (Deechit Poudel).
= in fine, Heisenberg regarde le côté granuleux de la lumière, et Huygens son côté ondelette.
(C'est aussi le sens de marche de mes explications qui donne un aspect à-rebours. En partant de la mécanique quantique, il est plus facile de passer par Heisenberg pour remonter vers les théories ondulatoires, ce qui est un contre-sens par rapport à la majorité des cours qui suivent le développement historique de la physique. Merci encore, jaravan.)
Jaravan, ta remarque est pertinente : l'optique est joyau poli pendant des siècles pour arriver à être capable de décrire la trajectoire d'un rayon lumineux à travers des lentilles, des fentes, etc.
Pour ma part, je part du constat suivant : un phénomène physique peut très souvent être plus ou moins bien être décrit par différents modèles : dans le cas de l'optique, le rayon lumineux peut être représenté par une droite toute droite, comme dans la harpe de JM Jarre :
Ou par un ensemble de points dont chaque point se transforme en cercle qui grandit, cercle fait de points qui à leur tour se transforme en cercles, répétés à l'infini :
Cet artifice mathématique est intéressant surtout lorsque la lumière rencontre un obstacle (comme en 2min35), ou un trou.
Pour faire court, la lumière, l'eau, le son, même un pet dans la nature s'expliquent mathématiquement avec ce principe. En poussant plus loin, on passe par Fraunhofer.
Comme en math on aime bien utiliser un nouvel outil sur toutes sortes d'expériences déjà résolues, on arrive à appliquer la transformée de Fourier en diffraction classique. Tant que ça simplifie les calculs, pourquoi pas ?
https://lob.epfl.ch/webdav/site/lob/users/113390/public/P1%20Fourier%20optics.pdf
Au lieu de travailler avec des nombres réels, on évite les sin et les cos en réécrivant une onde à l'aide des nombres complexes (le fameux i= racine de -1).
 . Et en plus les réactions des ondes peuvent s'expliquer par <psi l psi>, (psi au carré) ! Tiens, on s'approche dangereusement des états lpsi> quantiques !
. Et en plus les réactions des ondes peuvent s'expliquer par <psi l psi>, (psi au carré) ! Tiens, on s'approche dangereusement des états lpsi> quantiques !Puis Einstein, dit : l'effet photoélectrique (c'est-à-dire transformer de l'énergie lumineuse en énergie électrique) s'explique quand on modélise cet échange par des paquets d'énergie (des quantas), des boules quoi. En d'autres termes il dit que les vagues de l'océan (les ondes lumineuses) doivent être en forme de rocher (les quantas) quand elles buttent sur la berge métallique, pour que celle-ci recrache un morceau d'électricité (l'électron). Allô la Terre !

Plus tard, le Français de Broglie affirme la réciproque : si Einstein associe un paquet d'énergie (un caillou) à une onde lumineuse, pourquoi ne pas associer, une onde à chaque élément de matière (un électron-caillou par exemple) ?
En résumé : les cailloux qui passent à travers la fente unique se comportent comme un pet à travers la fente ! (ou, pour être précis dans le cas de de Broglie, suivent une trajectoire dictée par un vent mystérieux, non-détectable lui-même mais bien réel car ce vent fait dévier les cailloux).
Et c'est là qu'intervient le fameux h de Planck. C'est ce nombre qui fait le passage entre le monde des ondes, et le monde des particules. Effectivement les modèles classiques prédisent correctement les réactions d'une onde passant par une fente, mais la mécanique quantique - par son formalisme mathématique dual (onde-corpuscule) - décrivent non seulement ces phénomènes classiques, mais permirent la construction d'un microscope électronique, où la lumière utilisée dans un microscope optique qui traverse l'échantillon pour le révéler à nos yeux, est remplacée par un faisceau d'électrons, dont la longueur d'onde est plus petite. Par conséquent les électrons révèlent bien plus de détails, ce qui permet de zoomer plus loin. Et tout cela car on tient compte de cette dualité. De manière élégante dans la relation d'Heisenberg.
Pour aller plus loin : une expérience de salon proposé par un constructeur officiel :
https://www.phywe.com/en/diffraction-at-a-slit-and-heisenberg-s-uncertainty-principle.html#tabs1 Voir le mode d'emploi pour plus de détail.
D'autres commentaires : https://physics.stackexchange.com/questions/114227/interesting-relationship-between-diffraction-and-heisenbergs-uncertainty-princi
d'où est tirée la conclusion suivante :
"All in all, HUP considers the particle nature of light while Huygens' principle considers the wave nature of light." (Deechit Poudel).
= in fine, Heisenberg regarde le côté granuleux de la lumière, et Huygens son côté ondelette.
(C'est aussi le sens de marche de mes explications qui donne un aspect à-rebours. En partant de la mécanique quantique, il est plus facile de passer par Heisenberg pour remonter vers les théories ondulatoires, ce qui est un contre-sens par rapport à la majorité des cours qui suivent le développement historique de la physique. Merci encore, jaravan.)

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
I.3 l'onde ET la particule de de Broglie
Un des pères de la mécanique quantique, Louis de Broglie, qu'on a aperçu dans le poste précédent, a eu la géniale idée se lier à n'importe quelle particule -un électron - une onde. Pour lui, ils vivent simultanément dans notre monde, alors que pour la mécanique cantique orthodoxe, un objet quantique est soit onde (de probabilités dans le monde mathématique de Hilbert) soit particule (lorsqu'on essaie de détecter cet objet, il apparaîtra sous forme d'un grain qui laissera une trace bien réelle comme une tâche ou un clic sonore), mais pas les deux en même temps (du moins dans notre espace-temps).
Pour Louis en revanche, un objet quantique est fait simultanément d'une particule et d'une onde qui s'engendrent l'un l'autre.
Dans les années 2000, des chercheurs firent vibrer du silicone liquide dans une coupelle. En touchant la surface à l'aide d'un cure-dents, une sphère d'un millimètre de diamètre apparaît et qui interagit avec la surface sans se dissoudre, créant ainsi une onde. Tout se voit donc à l'oeil nu.
Si la goutte fait du sur-place, l'onde sera toujours la même, de même longueur d'onde (c'est-à-dire que la distance d'une bosse à une autre est toujours la même, même si ses bosses s'éloignent du centre).
Si la goutte retombe sur une surface un petit peu incliné, non seulement elle continuera à rebondir, mais aussi à se déplacer un peu horizontalement, guidée par son onde : la goutte + l'onde devient promeneuse ("walker").
Son déplacement semble alors chaotique.
Les walkers peuvent faire penser à des trous noirs qui brassent des ondes gravitationnelles, ou à deux étoiles qui dansent en modifiant leur espace-temps de leur entourage par les ondes qu'ils créent.
Ils semblent modéliser le déplacement des particules quantiques sans les détruire.
Ces gouttes peuvent aussi représenter la formation d'un cristal.
Bref, "The Lutetium Project" permet de rêver grâce à l'alliance de chercheurs et d'artistes qui font des vidéos. Si tu es artiste, n'hésite pas à entrer dans un labo pour proposer tes services. Les gens raffolent qu'on mettent leurs travaux en scène.
https://www.chipchip.ch/mondedesmontagnes
Ici, Camille Scherrer a eu le culot de frapper chez les geeks enfermés dans leur labo, pour leur proposer de construire un livre animé. Lorsqu'on tourne les pages de ce vrai livre éclairé par une lampe contenant une caméra, l'écran posé à côté réagit en temps réel. (Ce n'est donc pas la vidéo qui est intéressante, mais le livre !). Ça paraît old school, parce que ce cette technologie n'existait pas encore, sauf à l'état de recherche, il y a 10 ans de cela.
Enjoy !
Un des pères de la mécanique quantique, Louis de Broglie, qu'on a aperçu dans le poste précédent, a eu la géniale idée se lier à n'importe quelle particule -un électron - une onde. Pour lui, ils vivent simultanément dans notre monde, alors que pour la mécanique cantique orthodoxe, un objet quantique est soit onde (de probabilités dans le monde mathématique de Hilbert) soit particule (lorsqu'on essaie de détecter cet objet, il apparaîtra sous forme d'un grain qui laissera une trace bien réelle comme une tâche ou un clic sonore), mais pas les deux en même temps (du moins dans notre espace-temps).
Pour Louis en revanche, un objet quantique est fait simultanément d'une particule et d'une onde qui s'engendrent l'un l'autre.
Dans les années 2000, des chercheurs firent vibrer du silicone liquide dans une coupelle. En touchant la surface à l'aide d'un cure-dents, une sphère d'un millimètre de diamètre apparaît et qui interagit avec la surface sans se dissoudre, créant ainsi une onde. Tout se voit donc à l'oeil nu.
Si la goutte fait du sur-place, l'onde sera toujours la même, de même longueur d'onde (c'est-à-dire que la distance d'une bosse à une autre est toujours la même, même si ses bosses s'éloignent du centre).
Si la goutte retombe sur une surface un petit peu incliné, non seulement elle continuera à rebondir, mais aussi à se déplacer un peu horizontalement, guidée par son onde : la goutte + l'onde devient promeneuse ("walker").
Son déplacement semble alors chaotique.
Les walkers peuvent faire penser à des trous noirs qui brassent des ondes gravitationnelles, ou à deux étoiles qui dansent en modifiant leur espace-temps de leur entourage par les ondes qu'ils créent.
Ils semblent modéliser le déplacement des particules quantiques sans les détruire.
Ces gouttes peuvent aussi représenter la formation d'un cristal.
Bref, "The Lutetium Project" permet de rêver grâce à l'alliance de chercheurs et d'artistes qui font des vidéos. Si tu es artiste, n'hésite pas à entrer dans un labo pour proposer tes services. Les gens raffolent qu'on mettent leurs travaux en scène.
https://www.chipchip.ch/mondedesmontagnes
Ici, Camille Scherrer a eu le culot de frapper chez les geeks enfermés dans leur labo, pour leur proposer de construire un livre animé. Lorsqu'on tourne les pages de ce vrai livre éclairé par une lampe contenant une caméra, l'écran posé à côté réagit en temps réel. (Ce n'est donc pas la vidéo qui est intéressante, mais le livre !). Ça paraît old school, parce que ce cette technologie n'existait pas encore, sauf à l'état de recherche, il y a 10 ans de cela.
Enjoy !

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 dislocation d'un rayon lumineux
dislocation d'un rayon lumineux
Si on chevauche un rayon de lumière qui provient d'une énorme sphère en rotation comme le soleil, ce rayon de lumière n'aura pas le choix de se sectionner du à l'effet de rotation, s'il se détache de l'angle pour continuer son chemin en ligne droite suivant le parcourt de l'espace-temps, si on observe de plus près l'endroit ou il se sectionne on peut apercevoir des grains de lumière, c'est plus joli qu'une espèce de coupe franche et ça donne l'impression que le rayon est droit alors qu'il est décalé d'une poussière de degré. Quelle distance devrait-il parcourir l'un de l'autre pour ne plus que les deux rayons ne sois plus intriqué ensemble par leurs photons? 
J'ai eu cette petite réflexion…
J'ai eu cette petite réflexion…
 équation
équation

C'est tellement extraordinaire, sur la racine carrée de deux, l'infini apparait cela se précise plus cela devient imparfait cela permet d'évoluer dans toutes les dimensions mêmes si c'est impossible de tous les inclure, c'est tellement évidant que des que quelque chose lui touche le chat n'est plus à l'état mort et vivant à la fois, donc pas le choix de touché a un ou à l'autre ce qui donne une fabuleuse machine à probabilité.
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Tim, grand merci de poursuivre ton œuvre en dépit de l'adversité.
Sois certains que nous somme plusieurs à te lire avec délice même si on oublie trop souvent de te le dire.
Tu es bien seul à la barre depuis que ton compère Hobb nous a quitté, et tu n'en as que plus de mérites.
Si tu as besoin, afin d'étayer ce fil par quelques réflexions (/fractions) de haut vol j'ai des vidéos de chatons en stock.
Sois certains que nous somme plusieurs à te lire avec délice même si on oublie trop souvent de te le dire.
Tu es bien seul à la barre depuis que ton compère Hobb nous a quitté, et tu n'en as que plus de mérites.
Si tu as besoin, afin d'étayer ce fil par quelques réflexions (/fractions) de haut vol j'ai des vidéos de chatons en stock.

Confiteor- Messages : 9138
Date d'inscription : 01/04/2017
Age : 65
Localisation : Drôme
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Merci Confiteor ! Ca fait chaud au coeur.
Hobb, lui était le professionnel, ainsi que Badak (côté mathématique). Ce sont eux qui ont lancé le fil "j'aime les sciences" il y a quelques années, en donnant de l'impulsion. Et c'est Hobb qui m'a donné l'idée de passer par les maths. Il m'a donné souvent des feed-back, très denses, ainsi que des fil d'Ariane pour guider ce topic. Sans lui ce fil ne contiendrait pas autant de pages mathématiques. Badak m'a encouragé à poursuivre (ça veut dire que je n'ai pas écris trop de bêtises...).
Roger Penrose, le père des pavages, résume bien cela par des relations entre trois sphères :

La sphère physique, observable; la sphère mathématique (de Platon); la sphère mentale (l'imagination, perception, la métaphore).
En général le monde math est totalement occulté, et appris de manière linéaire en classe. Les validations physiques coûtent chers aussi, tout le monde ne peut pas s'amuser avec les appareils.

Quant à la dislocation, j'y répondrai prochainement dans la mesure de mes connaissances.
Hobb, lui était le professionnel, ainsi que Badak (côté mathématique). Ce sont eux qui ont lancé le fil "j'aime les sciences" il y a quelques années, en donnant de l'impulsion. Et c'est Hobb qui m'a donné l'idée de passer par les maths. Il m'a donné souvent des feed-back, très denses, ainsi que des fil d'Ariane pour guider ce topic. Sans lui ce fil ne contiendrait pas autant de pages mathématiques. Badak m'a encouragé à poursuivre (ça veut dire que je n'ai pas écris trop de bêtises...).
Roger Penrose, le père des pavages, résume bien cela par des relations entre trois sphères :

La sphère physique, observable; la sphère mathématique (de Platon); la sphère mentale (l'imagination, perception, la métaphore).
En général le monde math est totalement occulté, et appris de manière linéaire en classe. Les validations physiques coûtent chers aussi, tout le monde ne peut pas s'amuser avec les appareils.

Quant à la dislocation, j'y répondrai prochainement dans la mesure de mes connaissances.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
coucou ! eh bien je vois que le thème a beaucoup avancé ! merci tim9.5
une petite vidéo avec Etienne Klein :
une petite vidéo avec Etienne Klein :
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Salut Jérémy34 ! Ca fait longtemps que tu as lancé ce fil (j'ai oublié de te citer plus haut parmis les fondateurs !) En plus tu as progressé dans le cernement de la physique quantique, en trouvant une vidéo 1) d'un bon vulgarisateur 2) qui utilise des maths et des expériences physiques 3) et qui parle plus de 5 minutes 4) dans un débit apaisant.
Bravo !
Bravo !

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Bonjour a tous !
Tiens pour ceux que ca interesse, Etienne Klein fait une conference publique de vulgarisation au theatre de la Madeleine a Paris le 4 fevrier.
Sinon, j'ai des questions masse et Confiteor m'a gentillement indique que je pourrais les poser ici.
J'ai une formation universitaire en materiaux, donc j'ai quand meme les bases necessaires mais il y a des trucs que j'ai du mal a comprendre.
En fait, mon probleme, c'est de faire le lien entre la masse a l'echelle sub-nano (le boson de Higgs, que je comprends agir grosso modo comme une charge electrique qui attirerait les charges de meme sens) et ce qu'on constate a l'echelle macro.
Comment se fait-il par exemple que pour la gravitation, ce soit la masse totale de la Terre qui compte, et pas seulement celle des particules a portee immediate de l'objet considere (par ex, moi, soyons egocentriques) ? Comme la force diminue en 1/R2, on devrait constater un effet quasi-negligeable assez rapidement, non ?
Tiens pour ceux que ca interesse, Etienne Klein fait une conference publique de vulgarisation au theatre de la Madeleine a Paris le 4 fevrier.
Sinon, j'ai des questions masse et Confiteor m'a gentillement indique que je pourrais les poser ici.
J'ai une formation universitaire en materiaux, donc j'ai quand meme les bases necessaires mais il y a des trucs que j'ai du mal a comprendre.
En fait, mon probleme, c'est de faire le lien entre la masse a l'echelle sub-nano (le boson de Higgs, que je comprends agir grosso modo comme une charge electrique qui attirerait les charges de meme sens) et ce qu'on constate a l'echelle macro.
Comment se fait-il par exemple que pour la gravitation, ce soit la masse totale de la Terre qui compte, et pas seulement celle des particules a portee immediate de l'objet considere (par ex, moi, soyons egocentriques) ? Comme la force diminue en 1/R2, on devrait constater un effet quasi-negligeable assez rapidement, non ?
fift- Messages : 8844
Date d'inscription : 26/04/2016
Age : 48
Localisation : Paris
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Salut Fift! Le physicien pro ayant quitté le site, il nous est difficile de te répondre. Tu peux tenter ta chance sur https://physics.stackexchange.com
Je te conseille de clarifier ta question et de lui poser un cadre théorique (ici la gravité de Newton en tant qu’une force) mais en général on utilise la gravité dûe à l’espace temps (Einstein). De plus l’article du mois « pour la science » titre : et si la gravité n’etait pas quantique ?
Dans arxiv.org tu peux trouver des papiers de chercheurs en validation sur ce sujet. Bonne chasse!
Je te conseille de clarifier ta question et de lui poser un cadre théorique (ici la gravité de Newton en tant qu’une force) mais en général on utilise la gravité dûe à l’espace temps (Einstein). De plus l’article du mois « pour la science » titre : et si la gravité n’etait pas quantique ?
Dans arxiv.org tu peux trouver des papiers de chercheurs en validation sur ce sujet. Bonne chasse!

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Salut Fift! Le physicien pro ayant quitté le site, il nous est difficile de te répondre. Tu peux tenter ta chance sur https://physics.stackexchange.com
Je te conseille de clarifier ta question et de lui poser un cadre théorique (ici la gravité de Newton en tant qu’une force) mais en général on utilise la gravité dûe à l’espace temps (Einstein). De plus l’article du mois « pour la science » titre : et si la gravité n’etait pas quantique ?
Dans arxiv.org tu peux trouver des papiers de chercheurs en validation sur ce sujet. Bonne chasse!
Je te conseille de clarifier ta question et de lui poser un cadre théorique (ici la gravité de Newton en tant qu’une force) mais en général on utilise la gravité dûe à l’espace temps (Einstein). De plus l’article du mois « pour la science » titre : et si la gravité n’etait pas quantique ?
Dans arxiv.org tu peux trouver des papiers de chercheurs en validation sur ce sujet. Bonne chasse!

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
tim9.5 a écrit:De plus l’article du mois « pour la science » titre : et si la gravité n’etait pas quantique ?
Ouiii, excellent, synthétique, je peux le transmettre en pdf par mp à ceux qui le souhaitent !
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Merci à tous les deux !
The Kick Inside> comme je suis à l’etranger en ce moment et que je n’ai donc pas accès à la presse française, je veux bien l’article en pdf si ça ne te gêne pas.
The Kick Inside> comme je suis à l’etranger en ce moment et que je n’ai donc pas accès à la presse française, je veux bien l’article en pdf si ça ne te gêne pas.
fift- Messages : 8844
Date d'inscription : 26/04/2016
Age : 48
Localisation : Paris
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Salut fift, je ne suis pas sûr de comprendre ta question mais je vais essayer d'y répondre dans la limite de mes connaissances.
Tout d'abord je pense qu'il faut bien faire attention dans ce qu'on appelle "masse".
En fait le rôle clef du champ de Higgs est de permettre surtout aux bosons W et Z d'acquérir une masse et ainsi de fixer la portée très courte de l'interaction faible. Maintenant la gravitation serait portée elle même par un boson : le graviton, de masse nulle (si on admet qu'elle puisse être formulée dans un contexte similaire au modèle standard).
La masse au repos des particules -produite donc par brisure de symétrie dans le champ de Higgs- est en fait totalement négligeable pour l'interaction gravitationnelle classique, à la rigueur c'est l'énergie de liaison prise avec la masse au repos qui pourrait compter pour une telle interaction. Pour plus de détails :
https://physics.stackexchange.com/questions/230898/what-is-mass-in-particle-physics
Je tiens aussi à signaler que la définition de la masse dans le cadre de la relativité générale pose aussi problème :
https://en.m.wikipedia.org/wiki/Mass_in_general_relativity
Tout d'abord je pense qu'il faut bien faire attention dans ce qu'on appelle "masse".
En fait le rôle clef du champ de Higgs est de permettre surtout aux bosons W et Z d'acquérir une masse et ainsi de fixer la portée très courte de l'interaction faible. Maintenant la gravitation serait portée elle même par un boson : le graviton, de masse nulle (si on admet qu'elle puisse être formulée dans un contexte similaire au modèle standard).
La masse au repos des particules -produite donc par brisure de symétrie dans le champ de Higgs- est en fait totalement négligeable pour l'interaction gravitationnelle classique, à la rigueur c'est l'énergie de liaison prise avec la masse au repos qui pourrait compter pour une telle interaction. Pour plus de détails :
https://physics.stackexchange.com/questions/230898/what-is-mass-in-particle-physics
Je tiens aussi à signaler que la définition de la masse dans le cadre de la relativité générale pose aussi problème :
https://en.m.wikipedia.org/wiki/Mass_in_general_relativity
jaravan- Messages : 26
Date d'inscription : 01/08/2017
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Merci jaravan ! Ca m'ouvre des pistes ! Je vais essayer de me plonger là-dedans, car j'avoue avoir du mal à trouver des articles qui m'expliquent ce qu'est la masse.
Note qu'il faudrait peut-être que je commence par creuser du côté de la relativité générale, chose que j'avais assez laissé de côté jusqu'à présent.
Note qu'il faudrait peut-être que je commence par creuser du côté de la relativité générale, chose que j'avais assez laissé de côté jusqu'à présent.
fift- Messages : 8844
Date d'inscription : 26/04/2016
Age : 48
Localisation : Paris
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Lorsqu’on pose un objet sur une balance à deux plateau x, elle est déséquilibrée
http://www.jdecomarine.com/1887-large_default/balance-a-deux-plateaux-rotin.jpg
Je peux compenser en posant un certain objet dans l’autre plateau. Ces objets n’ont rien à voir l’un l’autre sauf le fait de rééquilibrer la balance. Cette propriété sera nommée « masse » (ou « poids » dans le langage courant, tandis que la physique ne parle pas de « poids » dans ce cas.
Ensuite on peut bifurquer dans l’algebre pour prouver l’addition des masses , la commutativité, l’associativité, l’élément neutre pour l’addition. C’est grâce à ses propopriétés qu’on peut mesurer la masse de l’air ambiant, en comparant la masse d’un ballon de basket vide, avec le même remplit par une pompe à air. On peut rajouter la multiplication et le 1 représenté par un objet de référence. Durant des sciences, l’etalon 1 kilo était un objet sous cloche. Mais avec les années il perdit de la masse! La métrologie est la science de la mesure. Actuellement elle veut tout faire reposer sur des constantes physiques universelles, retrouvant le partout. Depuis novembre 2018, le kilo est défini par la constante de Planck.
Pour plus d’info, voir https://www.rts.ch/info/sciences-tech/9984662-le-kilogramme-universel-redefini-grace-a-la-mecanique-quantique.html
Inutilisé pour cela une balance du Watt
En résumé la quantité de matière se nomme la masse.
La lumière n’a pas de masse. Elle ne fait réagir aucune balance. Les molécules ont une masse. Les atomes, électron, neutron, protons ont aussi une masse. Mais les protons et neutrons sont incassables. Ils sont formés de quark mais jamais à l’etat Isolé. On doit descendre dans ces profondeurs pour « rencontrer le boson de Higgs ». Mais comme on est dans le sub atomique, les particules sont vues comme des
Champs. D’où la théorie des champs développés dans les années 50. voilà en complément de jaravan.dans la relativite on distingue deux sortes de masses pour mieux les unir.
Pour obtenir
http://www.jdecomarine.com/1887-large_default/balance-a-deux-plateaux-rotin.jpg
Je peux compenser en posant un certain objet dans l’autre plateau. Ces objets n’ont rien à voir l’un l’autre sauf le fait de rééquilibrer la balance. Cette propriété sera nommée « masse » (ou « poids » dans le langage courant, tandis que la physique ne parle pas de « poids » dans ce cas.
Ensuite on peut bifurquer dans l’algebre pour prouver l’addition des masses , la commutativité, l’associativité, l’élément neutre pour l’addition. C’est grâce à ses propopriétés qu’on peut mesurer la masse de l’air ambiant, en comparant la masse d’un ballon de basket vide, avec le même remplit par une pompe à air. On peut rajouter la multiplication et le 1 représenté par un objet de référence. Durant des sciences, l’etalon 1 kilo était un objet sous cloche. Mais avec les années il perdit de la masse! La métrologie est la science de la mesure. Actuellement elle veut tout faire reposer sur des constantes physiques universelles, retrouvant le partout. Depuis novembre 2018, le kilo est défini par la constante de Planck.
Pour plus d’info, voir https://www.rts.ch/info/sciences-tech/9984662-le-kilogramme-universel-redefini-grace-a-la-mecanique-quantique.html
Inutilisé pour cela une balance du Watt
En résumé la quantité de matière se nomme la masse.
La lumière n’a pas de masse. Elle ne fait réagir aucune balance. Les molécules ont une masse. Les atomes, électron, neutron, protons ont aussi une masse. Mais les protons et neutrons sont incassables. Ils sont formés de quark mais jamais à l’etat Isolé. On doit descendre dans ces profondeurs pour « rencontrer le boson de Higgs ». Mais comme on est dans le sub atomique, les particules sont vues comme des
Champs. D’où la théorie des champs développés dans les années 50. voilà en complément de jaravan.dans la relativite on distingue deux sortes de masses pour mieux les unir.
Pour obtenir

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
fift a écrit:Merci à tous les deux !
The Kick Inside> comme je suis à l’etranger en ce moment et que je n’ai donc pas accès à la presse française, je veux bien l’article en pdf si ça ne te gêne pas.
J'avais pas vu ton message, je t'envoie ça demain !
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
merci à tous pour ce topic très intéressant, je m'y repenche peu à peu depuis le début, cette vulgarisation de haut vol donne un éclairage très intéressant et me fait comprendre pourquoi on ne se comprend pas
le background nécessaire à l'acquisition de ces savoirs est en effet extrêmement large
et souvent on ne parle donc pas des mêmes choses, une chaise n'est pas une chaise, chacun ayant sa "vision" de la chaise
la vision normalisée de la chaise quantique nécessite donc clairement l"acquisition de ce savoir, merci pour vos efforts :-)
sur la masse
https://www.futura-sciences.com/sciences/definitions/physique-masse-15213/
http://phys.free.fr/maspoids.htm
http://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/unites/unites.pdf
très intéressant on découvre , enfin moi je découvre :-)
les forces interagissent indirectement par échanges, les "ballons" dans la video, on peut alors se demander si par exemple le photon virtuel.. a lui même une masse définie par un bozon ?
en ce sens la masse de grand ballon de l'interaction faible et des petits ballons de l'interaction forte , seraient donnée par un bozon ?
pour le fun aaa jeunesse ennemie :-)
le background nécessaire à l'acquisition de ces savoirs est en effet extrêmement large
et souvent on ne parle donc pas des mêmes choses, une chaise n'est pas une chaise, chacun ayant sa "vision" de la chaise
la vision normalisée de la chaise quantique nécessite donc clairement l"acquisition de ce savoir, merci pour vos efforts :-)
sur la masse
https://www.futura-sciences.com/sciences/definitions/physique-masse-15213/
http://phys.free.fr/maspoids.htm
http://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/unites/unites.pdf
très intéressant on découvre , enfin moi je découvre :-)
les forces interagissent indirectement par échanges, les "ballons" dans la video, on peut alors se demander si par exemple le photon virtuel.. a lui même une masse définie par un bozon ?
en ce sens la masse de grand ballon de l'interaction faible et des petits ballons de l'interaction forte , seraient donnée par un bozon ?
pour le fun aaa jeunesse ennemie :-)
Dernière édition par zzebulon le Mer 6 Mar 2019 - 12:51, édité 2 fois
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
très pertinent, mr. zzebulon (oui, je suppose que tu es un mr., et j'accepte de me tromper)
Invité- Invité
Page 9 sur 16 •  1 ... 6 ... 8, 9, 10 ... 12 ... 16
1 ... 6 ... 8, 9, 10 ... 12 ... 16 
 Sujets similaires
Sujets similaires» documentaire:intro à la physique quantique...
» Conference interessante physique quantique
» Rayonnement du corps noir, et naissance de la physique quantique...
» ordinateur quantique
» The living matrix (physique quantique, médecine, champ d'information, intuition)
» Conference interessante physique quantique
» Rayonnement du corps noir, et naissance de la physique quantique...
» ordinateur quantique
» The living matrix (physique quantique, médecine, champ d'information, intuition)
Page 9 sur 16
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Évènements
Évènements