... un amoureux des maths dans le coin ?

J'ai cherché sans succès une rubrique "j'aime les chiffres et la géométrie"...
J'aime les chiffres mais surtout la géométrie.
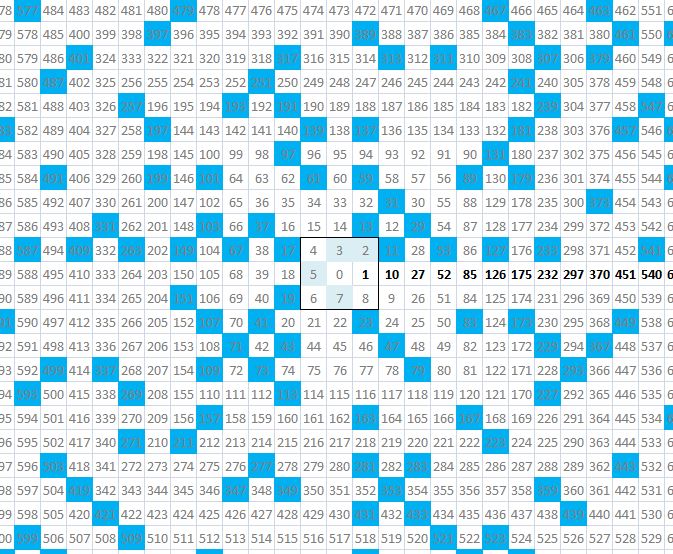
Je me suis retrouvée à faire ce tableau Excel et me suis rendu compte que les chiffres en gras, à savoir 1, 10, 27, 52, 85, 126... étaient appelés nombres décagonaux.

Une série de questions me vient à l'esprit (et oui, j'ai essayé de poser la question dans mon entourage, mais on m'a conseillé d'aller faire du shopping... )



QUESTION 1 : je n'ai rien trouvé de probant pour les autres lignes de chiffres :
3, 14, 33, 60, 95, 138...
5, 18, 39, 68, 105, 150...
7, 22, 45, 76, 115, 162...
...pourquoi ?

QUESTION 2 : que penser des suites :
8, 9, 26, 51, 84, 125...
6, 21, 44, 75, 114, 161...  ?

Merci d'avance...

Le fait que les nombres que tu as repérés soient décagonaux tient juste au fait qu'ils sont obtenus par le moyen d'une spirale, en commençant par 1, et que cela reproduit le schéma que l'on peut trouver ici : Decagonal number. Algébriquement, ils correspondent à la suite des valeurs 4n² - 3n.

Concernant la question 1, c'est-à-dire pour les autres directions du tableau, on peut trouver aussi des expressions algébriques. Par exemple, pour la demi-ligne 3, 14, 33, 60, 95, 138... c'est la suite des valeurs 4n² - n.

Concernant la question 2, on peut trouver aussi. Par exemple, pour la demi-ligne 6, 21, 44, 75, 114, 161... c'est la suite 4n² + 3n - 1.

Au départ, j'imagine que le but de la personne qui a créé ce tableau était d'étudier la distribution graphique des nombres premiers en fonction d'une énumération par la spirale, pas de trouver des relations géométriques ou algébriques. Mais ce n'est qu'une supposition.

Merci pour ta réponse si rapide, Pieyre, et désolée si ma question te semble un peu stupide (mon niveau en maths ne dépasse pas le stade bac)...
Et aussi merci pour le lien, je me limite par confort aux liens en français, c'est manifestement une erreur...

J'ai plusieurs versions de ce tableau, déclinées également avec des multiples, avec 0 ou 1 au centre... le but étant de m'amuser à trouver des motifs géométriques dans les arrangements spatiaux de chiffres... jeu commencé un jour d'ennui mortel dans une salle d'attente, comme ça m'a semblé prometteur, de retour à la maison, j'ai mis ça sous Excel... (on trouve des trucs très jolis, au passage   ) (et c'est pas pire qu'autre chose, comme passe-temps) (enfin, je crois   )
Évidemment, j'imaginais bien que ce genre de jeu avait déjà été longuement exploré, c'est d'ailleurs pour cette raison que j'ai posé la question ici...

J'insiste lourdement, mais : personne n'a de réponse à me proposer pour la question 2 ? Je me demandais, si, en prolongeant le tableau, j'allais finir par tomber sur un chiffre premier dans ces deux lignes... (auquel cas, problème réglé)

Si, je viens de répondre aussi à la question 2. Par ailleurs, excuse-moi; je n'avais pas compris que c'était toi qui avait fait ce tableau : j'avais lu trop vite.

Pieyre a écrit:
Concernant la question 2, on peut trouver aussi. Par exemple, pour la demi-ligne 6, 21, 44, 75, 114, 161... c'est la suite 4n² + 3n - 1.

nos éditions de message se sont croisées...

Pas de problème, pour ton dernier message... ^^

Maintenant, ne crois pas que j'ai trouvé ces relations algébriques à la main. J'ai juste fait une recherche sur le site de Stephen Wolfram. Mais j'aurais pu aussi le faire sur celui de Neil Sloane : OIES (où a collaboré Simon Plouffe, référence à connaître aussi quand on cherche à établir des relations numériques).

... j'avais commencé à essayer de trouver des formules, notamment avec certaines diagonales, sans grand succès, mon niveau en maths est trop limité (j'arrivais à des machins vraiment trop alambiqués pour être honnête...) du coup je vais tester aussi les diagonales sur le site OIES...
Merci...

J'ajoute qu'il est difficile de dire qu'un travail d'amateur ne permettra pas de trouver un résultat intéressant. Bon, en pure théorie des nombres, j'imagine que c'est râpé. Il vaudrait mieux partir d'un problème tellement spécifique que personne ne s'y sera intéressé.

Ainsi, concernant ta conjecture au sujet des nombres premiers, du moment qu'on dispose d'une expression algébrique pour caractériser une suite de nombres, certaines démonstrations sont immédiates. Par exemple, sur la demi-ligne des nombres décagonaux, dans la mesure où 4n² - 3n = n(4n - 3), eh bien automatiquement il n'y a pas de nombres premiers.

Pieyre a écrit: dans la mesure où 4n² - 3n = n(4n - 3), eh bien automatiquement il n'y a pas de nombres premiers.

... puisque divisible par (4n - 3) qui est différent de 1, j'imagine... oui, je comprends, effectivement.

Tiens, j'ai une question qui me dérange à ce sujet sur les chiffres premiers (attention, je ne suis pas une matheuse, ma logique est plutôt géométrique, donc illogique... ^^) : je sais que la définition est : divisible par lui-même et 1, mais ça ne me plait pas
- pour 1 (qui devrait être premier pour moi : après tout, il est divisible par "lui-même" et par 1, ce qui colle parfaitement à la définition)
- pour 2 (j'encaisse pas qu'un nombre premier soit pair : le côté "exception qui confirme la règle", ça me va en français, pas en maths) (en plus, ça crée une asymétrie visuelle dans mon tableau qui me dérange au regard des suites de la question 1 ^^).

Sais-tu si quelqu'un a déjà évoqué cette question ?

Je crois qu'à l'origine on considérait 1 comme premier : en effet, il n'est pas décomposable, ce qui correspond à l'intuition que l'on a quand on aborde la notion de nombre premier.

Mais, justement, que signifie qu'un nombre soit décomposable ? Qu'il soit factorisable. D'un point de vue opérationnel (que ce soit pour répartir le contenu d'un paquet de bonbons ou dans la perspective de construire un procédé cryptographique), c'est qu'il s'écrive d'une façon normalisée comme un produit minimal de puissances de facteurs non décomposables.

Ainsi 6 = 2 × 3 ou 12 = 2² × 3.
Mais 7 = 7, c'est déjà minimal; dire que 7 = 7 × 1 ne sert à rien (sinon pourquoi pas 7 = 7 × 1 × 1 aussi ?)

Alors, 2 et 3 correspondent à des façons de diviser de façon entière (comme dans le cas d'un paquet qui contient 60 bonbons), mais 1 ne sert à rien pour cela. Si tu manges ton paquet de bonbons toute seule (60 = 60 × 1 en quelque sorte) ou si tu le jettes à la poubelle (ici, il n'y a pas de division, mais on pourrait dire que 60 devient 0 d'une certaine façon, ce qui élimine aussi le cas 0 des nombres premiers et des nombres factorisables), eh bien il n'y a pas de partage, et pas de décomposition à effectuer.

1, 10, 27, 52, 85, 126...

3, 14, 33, 60, 95, 138...
5, 18, 39, 68, 105, 150...
7, 22, 45, 76, 115, 162...

9, 26, 51, 84, 125...
6, 21, 44, 75, 114, 161...

Je suis un grand 'fana' des chiffres, beaucoup moins de la géométrie.
J'ai commencé par regarder les chiffres seuls, sans m'intéresser au tableau, et j'ai des suites logiques qui me sont venues, la logique étant d'ailleurs la même dans chacune de ces séries, à une exception mineure près.
Le fait que cette logique soit la même s'explique d'ailleurs assez facilement par analyse géométrique (j'ai beau ne pas être fan de l'approche géométrique, je dois reconnaitre qu'elle a ses avantages).

Ces suites sont toutes définies par:
- U0=k (k étant le premier nombre de la suite, donc 1 dans le cas de la première suite que je cite, 3 pour la seconde, 5 pour la 3ème...)

-U1=2k+8 (sauf pour la suite commençant par un 6, où U1 = 2k+1+8, ce qui s'explique de façon géométrique: 1,3,5et7 sont au centre d'une face de leur carré, tandis que 6 est à un angle de son carré, et la suite commençant par 6 et partant en verticale vers le bas s'obtient en partant de celle commençant par 7 et allant dans le même sens, et en retranchant 1 à chaque élément : pour la suite commençant par 7, U0=7 et U1=2*7+8=22, pour celle commençant par 6, U0=7-1 et U1=22-1, ce qui ne fait pas 2*U0+8, mais 2*U0+9).

-Pour tout n>1, Un=2*U(n-1)-U(n-2)+8 (ou si vous préférez, Un= l'élément précédent + la différence entre les deux éléments précédents +8, ou encore, à chaque fois que n augmente de 1, la différence entre Un et U(n+1) augmente de 8 )

Exemple avec la première:
1, 10, 27, 52, 85, 126...
U0=1
U1=2*1+8 = 10
U2= 10 + (10-1) + 8 = 27
U3= 27+ (27-10) + 8 = 52
U4= 52+(52-27)+8 = 85
U5=85+41, U6=U5+49, U7=U6+57, U8=U7+65, etc

Ça marche avec toutes, vous pouvez vérifier si ça vous amuse

En partant de là, il n'y a rien de surprenant à ce que des formules à base de n² émergent, puisque l'on peut définir d'une façon très similaire la suite des nombres carrés:
1,4,9,16,25,36...

Ici, on a:
U0=1
U1= 2U0+2 = 4
Pour tout n>1, Un= 2*U(n-1)-U(n-2)+2 (même principe que précédemment, le +8 étant remplacé par un +2).
Ainsi, U2= 4+(4-1)+2 = 9
U3=9+(9-4)+2 = 16
U4 = 16+(16-9)+2=25
U5=U4+11, U6=U5+13, U7=U6+15...

Je reprend sur mes reflexions, avec les formules employant le n²

1,4,9,16,25...(la suite des carrés d'entiers positifs) est définie par:
U0=1
U1= 2 U0+ 2
Pour tout n>1, Un = 2U(n-1) - U(n-2) +2

1, 10, 27, 52, 85, 126... est définie par:
S0=1
S1= 2S0 + 8
Pour tout n>1, Sn = 2S(n-1) - S(n-2) +8

La suite S peut donc se définir à partir de la suite U:
S0= U0
S1 = U1 +6
S2 = 2S1 - S0 +8
    =2U1 + 12 -U0 + 8
    =2U1 - U0 + 2 + 18
    =U2 + 3*6
S3 =2S2 - S1 + 8
    =2U2 + 6*6 - U1 -6 + 6+2
    =2U2 - U1 +2 +6*6
    =U3 + 6*6
S4 = 2S3 -S2 +8
    = 2U3 + 12*6 - U2 - 3*6 + 6 +2
    = 2U3 - U2 + 2 +10*6
    = U4 + 10*6
et de façon plus générale, pour tout k>1:
Sk = 2S(k-1) -S(k-2) + 8
   = 2U(k-1) - U(k-2) +2 + s*6
   = Uk + s*6
s étant la somme des nombres allant de 1 à k (j'ai la démonstration en tête, mais la flemme de la coucher par écrit, je pourrais le faire à la demande).
Hors, la somme des nombres de 1 à k s'écrit plus joliment sous la forme de (k+1)*(k/2), ou encore (k²+k)/2
Donc:
Sk = Uk+ s*6
   = Uk + 6(k²+k)/2
   = Uk + 3(k²+k)
Et sachant que Uk = (k+1)², (U0=1², U1=2², U2=3²...), on obtient:
Sk = (k+1)² + 3(k²+k)
   = k²+2k+1+3k²+3k
   = 4k² + 5k +1


Je viens de démontrer (avec un petit creux au milieu de la démo, par flemme), que cette formule fonctionne pour tout k>1.
Elle fonctionne aussi pour k=1 (S1=10, 4*1² +5*1 +1 =10).
Ainsi que pour k=0 (S0=1, 4*0²+5*0+1 = 1)
je viens donc de démontrer que les nombres en gras du premier message (les décagonaux) correspondent algébriquement à la suite des valeurs 4k²+5k+1.

Et là, ce qui est très rigolo, c'est que Pieyre obtient:

Algébriquement, ils correspondent à la suite des valeurs 4n² - 3n.

Intuitivement, on se dit que l'un de nous s'est forcément planté.
Hors, aussi surprenant que ça puisse parraître, les deux sont justes (le point de départ des n et des k n'est pas le même, n=k+1).
Pour qu'aucun de nous ne se soit planté, il faudrait donc que pour tout entier k positif ou nul, et tout n = k+1, on ait ceci: 4n²-3n = 4k²+5k+1, ce qui est le cas.
Démonstration très simple:
4(k+1)²-3(k+1)= 4k²+8k+4-3k-3=4k²+5k+1

Autrement dit, pour faire court, j'ai démontré ici la formule de Pieyre.

Ça ne sert pas à grand chose, mais ça m'amuse

C'est très intéressant. Je ferai sans doute un commentaire à ce sujet plus tard.

Mais, en attendant, je me suis intéressé de façon plus attentive aux demi-droites du tableau qui n'intersectent aucun nombre premier.

Déjà il y a les quatre directions principales et les quatre diagonales, de façon évidente parce qu'elles incluent le 0, c'est-à-dire que la variable n qui désigne le n^ième nombre à partir du 0 intervient dans leur expression algébrique comme facteur.

Pour montrer cela, j'utilise quelques notations :
— la lettre A désigne la demi-droite principale, c'est-à-dire la demi-ligne horizontale (celle qui correspond aux nombre décagonaux);
— comme dans l'espace des nombres complexes, 1 désigne le vecteur horizontal et i le vecteur vertical (c'est plus minimal que (1, 0) et (0, 1)).

Aussi je peux faire l'inventaire des cas :

Les quatre directions principales

— A (droite) : 4n² - 3n = n(4n - 3)
— -A (gauche) : 4n² + n = n(4n + 1)
— iA (haut) : 4n² - n = n(4n - 1)
— -iA (bas) : 4n² + 3n = n(4n + 3)

Les quatre diagonales

— (1 + i)A (droite haut) : 4n² - 2n = n(4n - 2)
— (-1 + i)A (gauche haut) : 4n² = n(4n)
— (-1 - i)A (gauche bas) : 4n² + 2n = n(4n + 2)
— (1 - i)A (droite bas) : 4n² + 4n = n(4n + 4)

Les directions secondaires parallèles aux directions principales (je ne trouve que ces deux là mais il y en peut-être d'autres) :

— A - i : 4n² - 3n - 1 = (n - 1)(4n + 1) (à partir du rang 2)
— -iA - 1 : 4n² + 3n - 1 = (n + 1)(4n - 1) (à partir du rang 1)

Quant aux diagonales secondaires, apparemment il y en a énormément, ce qui se voit directement sur le tableau de Sybille, et ce qui mériterait à mon sens qu'on y réfléchisse.

Je n'en indique qu'une :

— (1 - i)A + i : 4n² - 4n + 1 = (2n - 1)² (à partir du rang 1)

Reste un problème : faut-il que l'expression qui correspond à une demi-droite (ligne, colonne ou diagonale, voire autre oblique) soit factorisable pour qu'elle n'intersecte aucun nombre premier ?

Asperzebre a écrit:Ça ne sert pas à grand chose, mais ça m'amuse

Moi je sens que ça va me prendre des plombes pour comprendre tous vos messages, à toi et Pieyre, vu mon niveau en maths, mais c'est hyper stimulant et j'adore !

Stegos, merci pour l'image, elle est MAGNIFIQUE
voilà ce que j'aime dans les maths : l'aspect visuel !

Pieyre a écrit:Je crois qu'à l'origine on considérait 1 comme premier : en effet, il n'est pas décomposable, ce qui correspond à l'intuition que l'on a quand on aborde la notion de nombre premier.

Mais, justement, que signifie qu'un nombre soit décomposable ? Qu'il soit factorisable. D'un point de vue opérationnel (que ce soit pour répartir le contenu d'un paquet de bonbons ou dans la perspective de construire un procédé cryptographique), c'est qu'il s'écrive d'une façon normalisée comme un produit minimal de puissances de facteurs non décomposables..............

Oui, de ce point de vue je comprends mieux.
Pour autant, ça continue de me heurter sur le plan géométrique... (et tu comprendras ainsi pourquoi je n'avais aucun avenir dans les filières scientifiques ^^)

Asperzebre a écrit: (j'ai la démonstration en tête, mais la flemme de la coucher par écrit, je pourrais le faire à la demande).

Je vais d'abord essayer de la faire moi-même (mais ça risque de prendre qqs temps quand même... ^^) ; je le prends comme un challenge... si je sèche, je t'appellerai à l'aide...

Au sujet des nombres premiers, d'un point de vue géométrique :

— 0 c'est rien; l'espace de représentation demeure vide;
— 1 c'est un point;
— 2 c'est deux points, forcément alignés;
— 3 c'est trois points, dont le plus simple est de les représenter de façon alignée (ou selon un triangle, mais là il n'est plus seulement question de divisibilité, ce qui était l'intérêt de l'introduction des nombres premiers);
— 4 c'est quatre points qu'on peut disposer en un carré; certes, c'est une figure géométrique comme le triangle mais c'est surtout une façon de représenter en deux dimensions deux séries de deux points : on en place deux sur une ligne et deux sur une ligne au dessus, de sorte qu'on rend compte du produit 2 × 2;
— 5 c'est comme 2 et 3 : des points alignés;
— 6 c'est un rectangle, de la même façon que 4 : 2 × 3;
— 7 c'est comme 2, 3 et 5;
— 8 c'est un cube : un carré à quatre points dans le plan et un carré identique dans la troisième dimension : 2 × 4, c'est-à-dire 2 × 2 × 2;
— 9 c'est un carré, comme 4 : 3 × 3.

Que remarque-t-on ? Les figures géométriques qui correspondent à des produits font intervenir des nombres minimaux, dont les premiers sont 2 et 3; si l'on va plus loin dans la liste, on obtient 5 (dans 10 = 2 × 5), 7 (dans 14 = 2 × 7), etc. Ce sont les nombres premiers.

https://www.youtube.com/watch?v=-X49VQgi86E

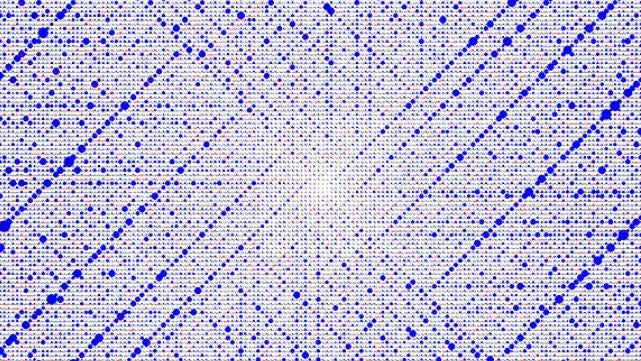
C'est la spirale d'Ulam..le truc découvert plus ou moins au hasard...et le truc méga frustrant...
Ça recense les nombres premiers....on à l'impression que les nombres premiers sont chaotiques, mais sous sa forme visuelle, il est clair que c'est pas le cas...donc il y a un truc à trouver..

Mais bonne chance quand même

Et...ça m’ennuierait quand même, vu qu'il m'arrive de faire de la crypto...et que cela repose sur les particularité des nombres premiers

Pieyre : merci, ça m'ouvre plein de perspectives, même si ma vision "géométrique" était plus spatiale, en fait (je m'exprime très mal, désolée), cette façon de voir les chiffres que tu présentes me plait beaucoup, je vais explorer tout ce qui est géométrie des chiffres...

Esteban : on peut toujours compter sur toi pour trouver des liens passionnants : comment fais-tu ???
Excellente, cette vidéo, c'est MAGNIFIQUE (et c'est exactement pour cette raison que j'aime la chose mathématique)

Stegos : bah Ulam c'était une conférence ennuyeuse (dixit my friend Google), moi une salle d'attente : -> des effets spiraux de l'ennui ? en tout cas il m'a grillée de 55 ans ! (le drame de ma vie : chaque fois que je pense trouver un truc sympa, il s'avère que qq'1 l'a fait avant moi... je passe mon temps à réinventer l'eau chaude ^^)
Donc, entre ça et mon niveau "bac" en maths...

Stegos a écrit:ça m’ennuierait quand même, vu qu'il m'arrive de faire de la crypto...et que cela repose sur les particularité des nombres premiers

... aucun risque...
(crypto, ça doit être sympa... un lien d'initiation pour les nulles ?)

Esteban : on peut toujours compter sur toi pour trouver des liens passionnants : comment fais-tu ??? Excellente, cette vidéo, c'est MAGNIFIQUE (et c'est exactement pour cette raison que j'aime la chose mathématique) a écrit:

L'intuition.

Salut tout le monde !
Wahou, je crois que je viens un peu trop tard...


Je ne sais pas si ça a déjà dit, mais je crois que l'on pourrait essayer de trouver une formule qui permettrait de calculer la formule d'une dans une spirale à n cotés pour une direction d. Je ne sais pas si je suis clair...

Ce que vous faites depuis le début, c'est de chercher pour toutes les directions d'une spirale "carrée" la formule donnant le n-ième terme dans une direction donnée.

Exemple:


Sibylle a déjà trouver que le n-ième nombre en gras depuis le centre, dans la direction 0 (horizontale), sont déjà les nombres décagonaux, donc, si je ne m'abuse, de formule 4n^2-3n.
Pieyre a trouvé pour la direction 2 (en tournant dans le sens inverse des aiguilles d'une montre, sens le plus courant car "positif") la formule 4n^2-n.
Etc.

Je pense que l'on pourrait essayer de trouver une formule unique avec une valeur donnant la direction de la suite pour unifier tout ça, et même le faire avec des spirales "triangulaires", "hexagonales", etc.


Aprè, pour la conjecture que tous les nombres premiers sont alignés, je ne sais pas si l'on peut relier ça avec une méthode que j'ai démontré pour la vérifier par moi-même:


Salut !

Tout d'abord je commente ton schéma.

Je ne vois pas bien ce que tu veux dire en parlant des nombres premiers tous alignés : en tant que points à une coordonnée correspondant à la demi-droite horizontale des abscisses positives, ils le sont par définition, qu'ils soient premiers ou non.

Alors, ce qui me paraît intéressant avec ce schéma, c'est qu'on obtient un crible d'Ératosthène généralisé, par la même méthode que ce savant a utilisée mais en conservant la trace des facteurs multiplicatifs, cela comme tu l'as fait en traçant les segments issus des points de la parabole de coordonnées entières. Ainsi le point (4, 2), qui correspond au facteur 2 en ordonnée, permet d'éliminer sur la droite des abscisses tous les nombres pairs, tout en conversant grâce aux segments tracés la raison pour laquelle ces nombres ne sont pas premiers, et même potentiellement leur décomposition en facteurs premiers (maintenant, pour 12, on lit 2 × 6 et 3 × 4, mais pas directement 2 × 2 × 3).

Une question : c'est de toi ou cela existait déjà, comme pour le schéma de Sybille ?


Par ailleurs, concernant ta question initiale, je m'étais efforcé de faire l'inventaire des formules que tu évoques, en tout point et toute direction de la grille, en plus de la place des nombres premiers et des positions proches du centre où les formules ne fonctionnement pas. Mais, le fait que la figure avait déjà étudiée par Ulam et d'autres, comme l'avait indiqué Stegos, m'avait un peu refroidi. Alors, j'ai tout de même repris cela hier, et voici ce que je peux dire.

En relation avec la question de trouver des formules, ce qui déjà me paraît intéressant ce sont les conventions formelles adoptées qui permettent de les concevoir et de les écrire de la façon la plus simple possible. Et là on peut errer un certain temps. En effet, faut-il commencer la spirale par le nombre 0 (comme Sybille) ou par le nombre 1 comme Ulam ? Ce n'est pas si évident. Ensuite, faut-il considérer les quatre directions sous la forme de décalages positifs relativement au centre ou bien à la façon d'un repère cartésien avec des coordonnées positives et négatives ? Ce n'est pas si évident non plus.

Personnellement, j'en suis resté à une origine à valeur 0 et quatre demi-axes à coordonnées positives, en raison de certaines régularités.

Ensuite, dans un réseau carré, il y a évidemment quatre directions, qui correspondent aux quatre changements d'orientation de la spirale, mais cela n'empêche pas d'envisager des directions supplémentaires. Ainsi nous avons assez facilement huit directions : les quatre demi-axes et les quatre demi-diagonales. En fonction du repère cartésien, j'avais premièrement envisagé des coordonnées standard. Mais, si on peut difficilement faire autrement que de désigner un point à partir duquel tracer une demi-droite par P (a, b), il n'empêche qu'il ne vaut mieux pas selon moi désigner une direction par un vecteur D = (u, v), avec u, v dans {-1, 0, 1} : il me paraît finalement préférable d'utiliser l'angle correspondant à cette direction (en radians : 0, π/4, π/2, 3π/4, ..., 7π/4).

Ainsi, en fonction de ces conventions, on obtient facilement les huit formules correspondant aux huit directions de l'espace considérées ici (auxquelles on pourrait en ajouter d'autres, comme π/3, qui correspondraient aussi à des formules) :

Pour un angle α, on a à partir de l'origine les formules : N = 4n² + (4/π α - 3)n, où n est le paramètre (le numéro de ligne ou de colonne positif relativement à l'origine) et N le nombre entier obtenu dans la grille : pour α = 0 les nombres décagonaux N = 4n² - 3n, pour α = π/4, les nombres N = 4n² - 2n, etc. jusqu'à N = 4n² + 4n pour α = 7π/4.

Par ailleurs, par construction, quand on décale le point de référence P (a, b) relativement à l'origine, on obtient facilement aussi les formules pour les huit directions de l'espace considérées (sauf celles qui reviennent vers le centre, dans la mesure où seules les directions qui ne recroisent pas les axes sont intéressantes, là où il y a une infinité de positions).

Déjà, il est facile d'obtenir les formules correspondant aux points qui se trouvent sur les demi-axes avec une direction orthogonale à ce demi-axe. Ainsi, puisque à l'origine O (0, 0), direction haut, on a N = 4n² - n, et direction bas : N = 4n² + 3n, eh bien on a pour le point A (a, 0), direction haut : N = 4n² - n + a et direction bas : N = 4n² - n - a; de même avec le point B (0, b) en prenant les directions droite et gauche de façon symétrique.

Ensuite, si l'on veut déterminer les formules correspondant aux diagonales, c'est du même genre : il suffit d'ajouter ou de retrancher l'abscisse ou l'ordonnée du point considérée à la formule de la diagonale valable pour le point O (et on traiterait de même toute direction oblique).

Et finalement, pour un point P (a, b) et une direction D = (u, v) en général, il suffit de trouver le point P' du demi-axe tel que le segment [P', P] soit orienté selon D : la formule est la même pour P et pour P' avec cette direction. En gros P' serait (a ± min (|a|, |b|), b ± min (|a|, |b|)).

C'est-à-dire qu'il ne serait pas très difficile d'exprimer cela avec une seule formule (mais de préférence une formule logique, ou disons informatique, avec des opérateurs de traitement par cas).

Je précise que la plupart de ces formules ne sont valables qu'à partir d'un certain rang, ce que je n'avais pas suffisamment fait la fois dernière. En effet, quand les demi-droites contiennent des suites d'entiers successifs à leur commencement, ce n'est pas significatif, ni pour trouver une formule ni pour déterminer la répartition des nombres premiers. Cela dénote le caractère un peu artificiel des pseudo-spirales polygonales.

Ainsi le fait de choisir une spirale basée sur le triangle, l'hexagone ou tout polygone régulier n'apporterait sans doute rien de tellement différent. En effet, pour le triangle, on considérerait les trois demi-droites passant par les sommets, qui déterminent entre elles un angle 2π/3 et pour l'hexagone un angle π/3. Cela permet d'ailleurs de penser qu'à fin de généralisation, il aurait mieux valu considérer dans le cas étudié les demi-droites passant par les sommets des carrés.

Quoi qu'il en soit, dans tous ces cas on doit obtenir des formules de type quadratique N = an² + bn + c, de même que, si l'on déployait une spirale en trois dimensions, on aurait des formules de type cubique, etc.

Maintenant, sur le fond, je ne crois pas que ces représentations géométriques puissent être tellement utile à fin d'étudier la répartition des nombres premiers. On voit certes se dessiner des structures (des droites pour une spirale à base de polygones ou de polyèdres réguliers ou des courbes particulières pour la spirale de Sacks, où sur certaines ne figurent pas de nombres premiers et pour d'autres quelques-uns, voire beaucoup). Mais, à mon avis, c'est juste dû au fait que ces figures, par construction, présentent des courbes paramétriques de type polynomial, et que les polynômes sont diversement factorisables de même que les nombres sont diversement décomposables en facteurs, ce qui interfère.

Mais ça, Euler l'annonçait déjà avec ses formules N = n² + n + 17 et N = n² - n + 41 qui permettent de générer beaucoup de nombres premiers.

N.B. – Tout cela est rédigé un peu vite. J'essaierai d'y mettre de l'ordre dans les jours suivants.

Dans un moment de crise numérique on avait énoncé que les nombres premiers ce sont des nombres qui ne sont pas rectangles ... Mais ça n'aide pas à les trouver.
Je cherche toujours une autre définition d'un nombre premier.
Si ta spirale carrée commence à 1, quelles différences ? Et si tu es dans une autre base que la base 10 ? Et en trois dimensions c'est quoi cette spirale ?

Pieyre, il me semble que le nombre pi ne définit pas ce qu'est un cercle, peux-tu me le confirmer stp ?

J'étudie un peu en ce moment les nombres de type a puissance a multiplié par b puissance b, également l'inverse est intéressant a puissance b multiplié par b puissance a, a et b entiers .

Si la spirale avait commencé en 0, on aurait eu à partir de ce point des séries en N = 4n² + an ± 1, ce qui aurait été moins minimal que N = 4n² + an. L'interprétation n'aurait pas été différente, bien sûr, mais il n'y a pas que le résultat qui compte. C'était tout le sujet de ma thèse de m'intéresser à la forme tout autant qu'au fond, enfin à l'expressivité d'une définition ou d'une démonstration tout autant qu'à sa rigueur et à son utilité.

Quant à la spirale de dimension 3 (ou 4 ou tout ce qu'on veut), ce n'est qu'une supposition de ma part, mais elle doit déjà être formalisée, forcément. Et, en effet, en recherchant sur un moteur de recherche, on en trouve diverses formes. Bon, elles ne correspondent pas à ce que je voulais dire, alors je précise d'un point de vue général.

Ce qui me paraît important relativement à la représentation des nombres (et notamment des nombres premiers) autrement que selon la demi-droite des entiers naturels (c'est-à-dire en dimension supérieure à 1), cela consiste en deux choses :
— parcourir un ensemble de positions de l'espace disposées de façon systématique, en gros sous la forme de sphères concentriques; le carré n'est jamais qu'une sphère en dimension 2 pour la topologie associée au maximum des deux coordonnées d'un point, de même que le cercle pour la topologie ordinaire; et en dimension 3 on a aussi bien la sphère au sens ordinaire que le cube ou d'autres formes;
— parcourir cet ensemble de façon continue, ou quasi-continue (puisqu'il s'agit de coordonnées entières); ainsi pour la spirale carrée on ne se contente pas d'empiler pas les carrés concentriques mais on embraie sur le carré suivant à la fin du carré inférieur; de même on peut considérer à trois dimensions des sphères imbriquées (fussent-elles des cubes) en embrayant sur la sphère englobante à la fin de la boule englobée, de sorte que l'on parcoure les positions de façon à appliquer toujours le même principe et dans le même sens, même si en certains points il y a une petite rupture de continuité.

Plus précisément, cela veut dire que l'on parcoure l'ensemble des positions des sphères concentriques successives (à la façon de pelure d'oignons), de sorte que les directions radiales (du centre vers l'extérieur, de façon orthogonale aux sphères) correspondent à un remplissage régulier des nombres qui s'enroulent selon les sphères des différents niveaux.

Je ne suis pas sûr d'être clair, mais c'est destiné à valoir pour toutes les dimensions. Disons, en dimension 3, qu'on parcoure un méridien en le tordant légèrement pour qu'il rejoigne après un tour de Terre le suivant; et qu'au moment où la ligne ainsi obtenue s'apprête à rejoindre le point initial, elle s'élève au-dessus du premier méridien parcouru pour refaire un parcours des méridiens de la Terre, mais un rang au dessus, et cela indéfiniment pour parcourir l'ensemble de l'espace à partir du centre de la Terre.

Quant au fait que le nombre pi caractérise ou non le cercle, tout dépend du cadre que l'on considère. Dans la topologie définie par la distance ordinaire d₂, le nombre pi intervient; mais si l'on considère les distances d₁ ou d_∞ (celle correspondant à la spirale carrée de ce sujet), il n'intervient pas.

Je rêve toujours d'une autre définition des nombres premiers. C'est quand même si étonnant, si beau qu'une si petite définition si simple amène à tellement de réflexions, comme 1/x qui au plus près du zéro amène à l'infini.
Si ça se trouve un nombre premier c'est dans un autre référentiel la hauteur des montagnes de plus de 3000 mètres, ou les noms numérisés des millionaires
Merci pour tes éclairages.
En tout cas, un carré ce n'est pas continu, c'est une différence par rapport à la spirale. D'ailleurs considérer le cercle comme un cas particulier de spirale, tu l'as certainement exploré. Quelle est vraiment la différence entre une spirale en 2d et une en 3d ? Cela veut dire une constante dans une partie des dimensions et un accroissement dans une autre dimension, et le cas particulier du cercle pour un accroissement de zéro.
Si cette spirale était un cercle, on n'additionerait pas les même nombres ?
Comment se place le nombre d'or là-dedans, lui que l'on retrouve dans la disposition des graines de tournesols par exemple ? Cette spirale carrée n'est pas avec le nombre d'or.

Pour rappel, 10=1+2+3+4 et pas seulement 2*5. Quelle forme serait avec 15 (1+2+3+4+5) de pourtour ? Le pentagone ou le triangle.