Pour les amateurs de Pi
4 participants
Page 1 sur 1
 Pour les amateurs de Pi
Pour les amateurs de Pi
Hello,
j'ai trouvé la formule suivante pour calculer pi :
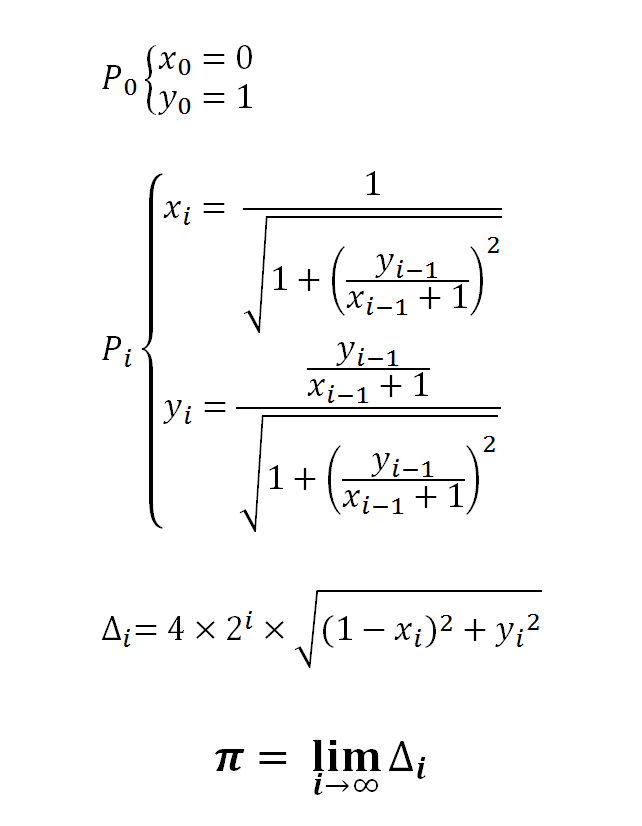
à part l'erreur (il faut multiplier par 2 et pas 4), ça marche programmé en java
oui je suis pas prof de lettres :->>
j'ai pas trouvé sur internet si elle avait déjà été trouvée...
si ça intéresse quelqu'un... en général non ! à part un vieux copain de lycée...
j'ai trouvé la formule suivante pour calculer pi :
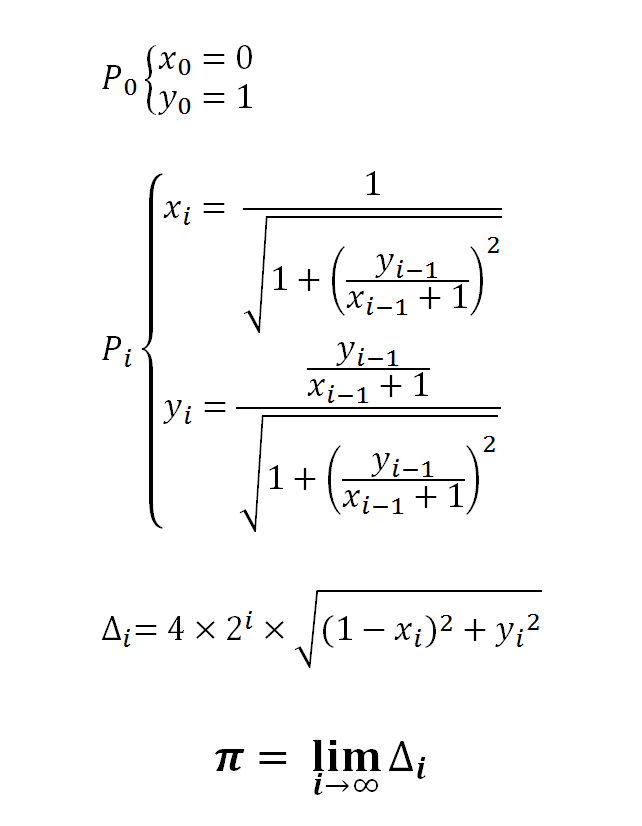
à part l'erreur (il faut multiplier par 2 et pas 4), ça marche programmé en java
oui je suis pas prof de lettres :->>
j'ai pas trouvé sur internet si elle avait déjà été trouvée...
si ça intéresse quelqu'un... en général non ! à part un vieux copain de lycée...
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Wahou ! Jusqu'à combien de décimale as-tu calculé pi ? Et peux-tu comparer la vitesse d'exécution avec d'autres algorithmes ?
Tu connais certainement cette playlist :
ou la manière de mémoriser pi de Daniel Tammet ?
Une autre passionnée de pi, qui fête ce nombre chaque 3/14/année (date américaine), et qui le chante:
Tu n'es pas tout seul, ProfdeLettre
Tu connais certainement cette playlist :
ou la manière de mémoriser pi de Daniel Tammet ?
Une autre passionnée de pi, qui fête ce nombre chaque 3/14/année (date américaine), et qui le chante:
Tu n'es pas tout seul, ProfdeLettre

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
J'ai pas calculé bc de décimal... mais c'ets intéressant de voir que ça converge vite :
0 : 2.8284271247461903
1 : 3.0614674589207187
2 : 3.1214451522580524
3 : 3.136548490545939
4 : 3.1403311569547534
5 : 3.1412772509327733
6 : 3.1415138011443013
7 : 3.141572940367092
8 : 3.14158772527716
9 : 3.1415914215112
10 : 3.141592345570118
11 : 3.141592576584873
12 : 3.141592634338563
13 : 3.141592648776986
14 : 3.141592652386591
15 : 3.1415926532889924
16 : 3.141592653514593
17 : 3.141592653570993
18 : 3.141592653585093
19 : 3.141592653588617
20 : 3.1415926535894987
21 : 3.141592653589719
22 : 3.1415926535897745
23 : 3.1415926535897882
24 : 3.141592653589792
25 : 3.1415926535897927
26 : 3.1415926535897927
27 : 3.1415926535897927
28 : 3.1415926535897927
29 : 3.1415926535897927
30 : 3.1415926535897927
31 : 3.1415926535897927
32 : 3.1415926535897927
33 : 3.1415926535897927
34 : 3.1415926535897927
35 : 3.1415926535897927
36 : 3.1415926535897927
37 : 3.1415926535897927
38 : 3.1415926535897927
39 : 3.1415926535897927
en fait le principe est assez simple. il s'agit de calculer la circonférence d'un polygone avec n^2 côtés.
donc on calcule la longeur d'un côté multiplié par le nombre.
au début on commence avec un carré (losange régulier si on veut).
après un octogone, etc. c'est pour ça que c'est une suite.
on calkcule la longeur du nouveau côté avec pythagore (c'est pour ça qu'on se retrouve avec des racines de sommes de carrés).
voilà, après on multiplie par le nb de côtés.
du coup la formule donne la circonférence du cercle, d'où l'erreur, 2Pi au lieu de Pi...
0 : 2.8284271247461903
1 : 3.0614674589207187
2 : 3.1214451522580524
3 : 3.136548490545939
4 : 3.1403311569547534
5 : 3.1412772509327733
6 : 3.1415138011443013
7 : 3.141572940367092
8 : 3.14158772527716
9 : 3.1415914215112
10 : 3.141592345570118
11 : 3.141592576584873
12 : 3.141592634338563
13 : 3.141592648776986
14 : 3.141592652386591
15 : 3.1415926532889924
16 : 3.141592653514593
17 : 3.141592653570993
18 : 3.141592653585093
19 : 3.141592653588617
20 : 3.1415926535894987
21 : 3.141592653589719
22 : 3.1415926535897745
23 : 3.1415926535897882
24 : 3.141592653589792
25 : 3.1415926535897927
26 : 3.1415926535897927
27 : 3.1415926535897927
28 : 3.1415926535897927
29 : 3.1415926535897927
30 : 3.1415926535897927
31 : 3.1415926535897927
32 : 3.1415926535897927
33 : 3.1415926535897927
34 : 3.1415926535897927
35 : 3.1415926535897927
36 : 3.1415926535897927
37 : 3.1415926535897927
38 : 3.1415926535897927
39 : 3.1415926535897927
en fait le principe est assez simple. il s'agit de calculer la circonférence d'un polygone avec n^2 côtés.
donc on calcule la longeur d'un côté multiplié par le nombre.
au début on commence avec un carré (losange régulier si on veut).
après un octogone, etc. c'est pour ça que c'est une suite.
on calkcule la longeur du nouveau côté avec pythagore (c'est pour ça qu'on se retrouve avec des racines de sommes de carrés).
voilà, après on multiplie par le nb de côtés.
du coup la formule donne la circonférence du cercle, d'où l'erreur, 2Pi au lieu de Pi...
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Salut,
sympa comme formule oui, ce qui serait plus intéressant encore serait de trouver la vitesse de convergence (i.e. combien de nouvelles décimales tu trouves à chaque itération) ;-)
sympa comme formule oui, ce qui serait plus intéressant encore serait de trouver la vitesse de convergence (i.e. combien de nouvelles décimales tu trouves à chaque itération) ;-)
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Ta formule est une variante de l’algorithme d’Archimède, non?
http://scalion.free.fr/calculpi.htm
http://scalion.free.fr/calculpi.htm

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
tim9.5 a écrit:Ta formule est une variante de l’algorithme d’Archimède, non?
http://scalion.free.fr/calculpi.htm
Oui, un peu optimisée (on n'incrémente pas le nombre de coté de 1 à chaque fois, on multiplie par 2). Du coup ça converge plus vite ;-)
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
oui c'est ça
edit. ben l'intérêt c'est que y'a pas de cos aussi... donc ça simplifie car le calcul d'un cos est en tant que tel le résultat d'une suite, non ?
ceci dit la description du lien c'est aussi des puissances de 2 mais y'a du cos dans le pgrm donc c'ets peut être pas le pgrm qui correspond mais j'ai pas bien regardé non plus.
edit. ben l'intérêt c'est que y'a pas de cos aussi... donc ça simplifie car le calcul d'un cos est en tant que tel le résultat d'une suite, non ?
ceci dit la description du lien c'est aussi des puissances de 2 mais y'a du cos dans le pgrm donc c'ets peut être pas le pgrm qui correspond mais j'ai pas bien regardé non plus.
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Dans l'algorithme d'Archimède il n'y en a pas non plus. En fait dans aucun algorithme intéressant il n'y en a (cosinus, sinus etc font intrinsèquement intervenir pi). Sinon, ça serait un peu comme dire "comment calculer pi à partir de fonctions qui sont basées sur lui". Ca n'a pas d'intérêt.
Par contre chose amusante : racine (1 - un truc au carré), en général ça renvoie à de la trigo (puisque cos = racine (1 - sin ²) )
Par contre chose amusante : racine (1 - un truc au carré), en général ça renvoie à de la trigo (puisque cos = racine (1 - sin ²) )
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Et pourrait-on calculer la suite des décimales avec cette fonction ? Il devrait avoir une simple astuce de programmation pour "décaler" le calcul par paquets.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Non justement... a chaque itération, si tu n'as pas la totalité des décimales, tu n'auras pas les arrondis... et donc pas le bon résultat (c'est bien là tout le problème...).
Il existe un algorithme "compte-goutte" (basé sur pi écrit en base à pas variable d'Euler), mais elle nécessite une quantité de mémoire encore plus grande... :-/
A ma connaissance il n'y a pas d'algorithme non probabiliste permettant de calculer pi par paquet (sinon atteindre des décimales très loin ne serait plus en un exploit ;-) )
Il existe un algorithme "compte-goutte" (basé sur pi écrit en base à pas variable d'Euler), mais elle nécessite une quantité de mémoire encore plus grande... :-/
A ma connaissance il n'y a pas d'algorithme non probabiliste permettant de calculer pi par paquet (sinon atteindre des décimales très loin ne serait plus en un exploit ;-) )
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Ça serait bien sympa de poster le programme.
Tu vas jusqu'à quelle précision avec Java ?
Informatiquement, les racines et les puissances sont des calculs effectués à partir de représentations approximatives des nombres en base 2, sauf à utiliser des bibliothèques spécialisées. Donc tes variables doivent au moins être d'une précision égale à celle que tu veux calculer pour PI.
(non, je ne suis pas un siamois )
)
Question subsidiaire : Philosophiquement, est-ce que PI définit un cercle ?
Tu vas jusqu'à quelle précision avec Java ?
Informatiquement, les racines et les puissances sont des calculs effectués à partir de représentations approximatives des nombres en base 2, sauf à utiliser des bibliothèques spécialisées. Donc tes variables doivent au moins être d'une précision égale à celle que tu veux calculer pour PI.
(non, je ne suis pas un siamois
Question subsidiaire : Philosophiquement, est-ce que PI définit un cercle ?
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
siamois93 a écrit: sauf à utiliser des bibliothèques spécialisées.
Toutes les bibliothèques bossent intrinsèquement en base de 2.
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Hobb : Tu es informaticien ?
On peut bosser avec des entiers tant qu'on est avec des rationnels.
On aurait alors une précision totale pour PI au carré.
On peut bosser avec des entiers tant qu'on est avec des rationnels.
On aurait alors une précision totale pour PI au carré.
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Mathématiquement, π définit la longueur d'un truc rond, π² définit la surface d'un cercle, π³ définit le volume d'une sphère.siamois93 a écrit:Question subsidiaire : Philosophiquement, est-ce que PI définit un cercle ?
Si, dans une équation, tu te retrouves avec un π qui traîne, il y a probablement un truc "rond" dans le coin, et la puissance de π associée te permet de savoir dans quel espace tu évolues. Si le π n'a "a priori" rien a faire là...ou bien c'est une erreur de calcul, ou bien tu n'as pas vraiment compris un truc au problème.
Et si tu as un π⁴, π⁵, π⁶ etc etc..alors ou bien tu bosses avec des espaces de dimensions > 3, ou bien tu es probablement en train de te vautrer
Maintenant, Philosophiquement....

Stegos- Messages : 4567
Date d'inscription : 18/02/2018
Age : 105
Localisation : 3ème planète autour du soleil
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
siamois93 a écrit:Hobb : Tu es informaticien ?
non [enfin pas dans le sens où vous l'entendez]
siamois93 a écrit:
On peut bosser avec des entiers tant qu'on est avec des rationnels.
Non plus, si je veux bosser avec 1/3 (qui est rationnel), je ne peux pas exactement l'approximer avec un entier
siamois93 a écrit:
On aurait alors une précision totale pour PI au carré.
Ce n'est déjà pas le cas pour les rationnels, donc pour les irrationnels comme pi, encore moins...
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Ben oui, parce que philosophiquement, le cercle et le carré.... Un compas est un outil qui sert à reporter une distance, et avec un compas et une règle on peut tracer des perpendiculaires. Pi s'approxime avec différentes suites, et je trouve intéressant de se dire qu'un cercle, un truc rond quoi, est lié à une alternance de fractions de nombres impairs par exemple. C'est plus un questionnement sur le sens des nombres.
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Stegos a écrit:Mathématiquement, π définit la longueur d'un truc rond, π² définit la surface d'un cercle, π³ définit le volume d'une sphère.siamois93 a écrit:Question subsidiaire : Philosophiquement, est-ce que PI définit un cercle ?
Si, dans une équation, tu te retrouves avec un π qui traîne, il y a probablement un truc "rond" dans le coin, et la puissance de π associée te permet de savoir dans quel espace tu évolues. Si le π n'a "a priori" rien a faire là...ou bien c'est une erreur de calcul, ou bien tu n'as pas vraiment compris un truc au problème.
Et si tu as un π⁴, π⁵, π⁶ etc etc..alors ou bien tu bosses avec des espaces de dimensions > 3, ou bien tu es probablement en train de te vautrer
Maintenant, Philosophiquement....
c'est pas vraiment pi qui est élevé à une puissance, c'ets plutot le rayon. pi est juste un rapport donc sans dimension
re-edit par contre on peut se demander la signification des puissances de pi et de ses racines qui apparaissent aussi à l'occasion, comme résultats d'intégrales par exemple
edit
siamois93 a écrit:Ben oui, parce que philosophiquement, le cercle et le carré.... Un compas est un outil qui sert à reporter une distance, et avec un compas et une règle on peut tracer des perpendiculaires. Pi s'approxime avec différentes suites, et je trouve intéressant de se dire qu'un cercle, un truc rond quoi, est lié à une alternance de fractions de nombres impairs par exemple. C'est plus un questionnement sur le sens des nombres.
un carré est quelque chose de discontinu. pour passer au cercle il faut une notion d'infini entre les deux. comme un polygone régulier avec un nombre infini de côtés. c'est peut-être pour ça qu'il faut une suite infinie pour exprimer pi avec des nombres finis
Dernière édition par ProfDeLettres le Mer 30 Oct 2019 - 12:34, édité 1 fois
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
@Hobb: Bon, on a un problème pour se comprendre, mais vu que t'es pas informaticien, ça me parait normal.
Quand tu parles de 1/3, 3 c'est bien un entier, ou tu préfères déjà lui faire perdre de la précision en l'écrivant sous forme d'une puissance de 2 ?
En plus dans un processeur, les entiers (selon la taille du processeur) ne sont pas manipulés comme quand on utilise des algorithmes externes, donc il y a plein d'intérêts à utiliser des entiers.
Quand tu parles de 1/3, 3 c'est bien un entier, ou tu préfères déjà lui faire perdre de la précision en l'écrivant sous forme d'une puissance de 2 ?
En plus dans un processeur, les entiers (selon la taille du processeur) ne sont pas manipulés comme quand on utilise des algorithmes externes, donc il y a plein d'intérêts à utiliser des entiers.
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
siamois93 a écrit:
Quand tu parles de 1/3, 3 c'est bien un entier, ou tu préfères déjà lui faire perdre de la précision en l'écrivant sous forme d'une puissance de 2 ?
Vous l'exprimez comme vous voulez, à partir du moment où les bibliothèques passent par du binaire, ça passe forcément en puissance de 2... (même s'il s'agit de 0.333333...)
siamois93 a écrit:
En plus dans un processeur, les entiers (selon la taille du processeur) ne sont pas manipulés comme quand on utilise des algorithmes externes, donc il y a plein d'intérêts à utiliser des entiers.
Heu là désolé, mais cette phrase ne veut rien dire. Bibliothèques "externes" ou pas (pas "algorithme externe" qui ne veut rien dire, pour commencer...), in fine c'est le processeur qui se coltine les calculs... Et ça veut dire quoi qu'ils ne sont pas manipulés pareils ...? A part certains détails (type quelques bibliothèques spécifiques grand-nombres, où les entiers sont explicitement stockés dans des tableaux, ce qui nécessite le redéveloppement de tout l’attirail des fonctions de l'APU, mais bref), ils sont tous manipulés exactement pareils, avec les mêmes types (encodés selon la norme IEEE-754 pour les flottants, calculs classiques à l'endianness près pour les entiers si vous voulez du détail). Les dites-bibliothèques "grand-nombre" manipulent aussi bien des flottants (le must pour ce genre de calcul étant les virgules fixes, mais passons) que des entiers, donc non, aucun intérêt à manipuler des entiers (puisqu'à un moment, de toutes façons, on essaye bien de calculer un réel...).
Et ça ne dépend pas de la "taille" du processeur (Laquelle ? o_O)...
Et pour terminer, à cause des erreurs d'arrondis, il ne sagit pas d'algorithmes déterministes dans le sens où si vous voulez estimer la 1000ème décimale de pi, avec des approches comme celles-ci, il vous faudra calculer largement au-delà de 1000 décimales.
siamois93 a écrit:@Hobb: Bon, on a un problème pour se comprendre, mais vu que t'es pas informaticien, ça me parait normal.
Heu, pas informaticien donc je ne connais pas l'informatique... ?
Là désolé, mais informaticien ou pas, on se comprend mal parce que vous n'utilisez pas le bon vocabulaire... algorithme /= bibliothèque, taille d'encodage /= taille de processeur, etc.
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
@Prof : Dans l'angle il n'y aura jamais de tangente, elle n'est pas définie à ce point.
Il me semble, c'est ancien quand même, qu'un carré est continu, mais la fonction carré n'est pas dérivable en tout point, les fameux angles.
Alors, ton programme, tu le montre quelque part ?
Il me semble, c'est ancien quand même, qu'un carré est continu, mais la fonction carré n'est pas dérivable en tout point, les fameux angles.
Alors, ton programme, tu le montre quelque part ?
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
- C:
- Code:
/*
* Computation of the n'th decimal digit of \pi with very little memory.
* Written by Fabrice Bellard on January 8, 1997.
*
* We use a slightly modified version of the method described by Simon
* Plouffe in "On the Computation of the n'th decimal digit of various
* transcendental numbers" (November 1996). We have modified the algorithm
* to get a running time of O(n^2) instead of O(n^3log(n)^3).
*
* This program uses mostly integer arithmetic. It may be slow on some
* hardwares where integer multiplications and divisons must be done
* by software. We have supposed that 'int' has a size of 32 bits. If
* your compiler supports 'long long' integers of 64 bits, you may use
* the integer version of 'mul_mod' (see HAS_LONG_LONG).
*/
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
/* uncomment the following line to use 'long long' integers */
/* #define HAS_LONG_LONG */
#ifdef HAS_LONG_LONG
#define mul_mod(a,b,m) (( (long long) (a) * (long long) (b) ) % (m))
#else
#define mul_mod(a,b,m) fmod( (double) a * (double) b, m)
#endif
/* return the inverse of x mod y */
int inv_mod(int x, int y)
{
int q, u, v, a, c, t;
u = x;
v = y;
c = 1;
a = 0;
do {
q = v / u;
t = c;
c = a - q * c;
a = t;
t = u;
u = v - q * u;
v = t;
} while (u != 0);
a = a % y;
if (a < 0)
a = y + a;
return a;
}
/* return (a^b) mod m */
int pow_mod(int a, int b, int m)
{
int r, aa;
r = 1;
aa = a;
while (1)
{
if (b & 1)
r = mul_mod(r, aa, m);
b = b >> 1;
if (b == 0)
break;
aa = mul_mod(aa, aa, m);
}
return r;
}
/* return true if n is prime */
int is_prime(int n)
{
int r, i;
if ((n % 2) == 0)
return 0;
r = (int) (sqrt(n));
for (i = 3; i <= r; i += 2)
if ((n % i) == 0)
return 0;
return 1;
}
/* return the prime number immediatly after n */
int next_prime(int n)
{
do
{
n++;
} while (!is_prime(n));
return n;
}
int main(int argc, char *argv[])
{
int av, a, vmax, N, n, num, den, k, kq, kq2, t, v, s, i;
double sum;
if (argc < 2 || (n = atoi(argv[1])) <= 0)
{
printf("This program computes the n'th decimal digit of \\pi\n"
"usage: pi n , where n is the digit you want\n");
exit(1);
}
N = (int) ((n + 20) * log(10) / log(2));
sum = 0;
for (a = 3; a <= (2 * N); a = next_prime(a))
{
vmax = (int) (log(2 * N) / log(a));
av = 1;
for (i = 0; i < vmax; i++)
av = av * a;
s = 0;
num = 1;
den = 1;
v = 0;
kq = 1;
kq2 = 1;
for (k = 1; k <= N; k++)
{
t = k;
if (kq >= a)
{
do
{
t = t / a;
v--;
} while ((t % a) == 0);
kq = 0;
}
kq++;
num = mul_mod(num, t, av);
t = (2 * k - 1);
if (kq2 >= a)
{
if (kq2 == a)
{
do {
t = t / a;
v++;
} while ((t % a) == 0);
}
kq2 -= a;
}
den = mul_mod(den, t, av);
kq2 += 2;
if (v > 0)
{
t = inv_mod(den, av);
t = mul_mod(t, num, av);
t = mul_mod(t, k, av);
for (i = v; i < vmax; i++)
t = mul_mod(t, a, av);
s += t;
if (s >= av)
s -= av;
}
}
t = pow_mod(10, n - 1, av);
s = mul_mod(s, t, av);
sum = fmod(sum + (double) s / (double) av, 1.0);
}
printf("Decimal digits of pi at position %d: %09d\n", n,
(int) (sum * 1e9));
return 0;
}

Stegos- Messages : 4567
Date d'inscription : 18/02/2018
Age : 105
Localisation : 3ème planète autour du soleil
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
- F90:
- Code:
program pi
real(8) :: x = 0., y = 1., xtmp, pi0 = 0., pi1 = 1., i = 1
do while (pi0 /= pi1)
xtmp = x ; pi0 = pi1
x = 1./sqrt(1.+(y/(x+1.))**2)
y = (y/(xtmp+1.))/sqrt(1.+(y/(xtmp+1.))**2)
pi1 = 2**(i+1)*sqrt((1.-x)**2+y**2)
i = i + 1
write(*,*) i - 1, pi1
enddo
end program
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
java
(le nom "hello" pour le package est important)
@Siamois
on peut se demander à quoi ça sert de calculer le plus de décimals de Pi. parce que même plusieurs billons c'est toujours rien par rapport à l'infini. C'est un record comme un autre ceci dit. Mais à quoi servent les records ? A la satisfaction de l'ego ? ;-)
on peut se demander aussi comment ça se fait que la valeur d'un nombre conceptuellement très simple à définir soit si compliqué à exprimer ?
- Code:
package hello;
public class Pi {
static private class Point {
double x, y;
}
static Point computeNextPoint(Point p) {
Point nextP = new Point();
double determnant = p.y/(p.x + 1);
double doe = auCarré(determnant);
nextP.x = Math.sqrt(((double) 1) / (1 + doe));
nextP.y = determnant * nextP.x;
return nextP;
}
static double computeQuadre(int i, Point p) {
return ((double) 2) * Math.pow(2, i) * Math.sqrt(auCarré(1 - p.x) + auCarré(p.y)) ;
}
static double auCarré(double d) {
return d * d;
}
public static void main(String[] args) {
Point p = new Point();
p.x = 0;
p.y = 1;
for (int i = 0; i < 100; i++) {
System.out.println(i + " : " + computeQuadre(i, p));
p = computeNextPoint(p);
}
}
}
(le nom "hello" pour le package est important)
@Siamois
on peut se demander à quoi ça sert de calculer le plus de décimals de Pi. parce que même plusieurs billons c'est toujours rien par rapport à l'infini. C'est un record comme un autre ceci dit. Mais à quoi servent les records ? A la satisfaction de l'ego ? ;-)
on peut se demander aussi comment ça se fait que la valeur d'un nombre conceptuellement très simple à définir soit si compliqué à exprimer ?
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
ProfDeLettres a écrit:C'est un record comme un autre ceci dit. Mais à quoi servent les records ? A la satisfaction de l'ego ? ;-)
Aux outils à mettre en oeuvre, à l'avancée technique et scientifique pour atteindre de tels niveaux ;-)
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
@Stegos : argv[0] c'est quand même plus mignon que le nom en dur, qu'en penses-tu ?
@ProfDeLettres : Oui c'est certain, l'infini, c'est énorme. Un point autrement intéressant est la question du passage aux limites.
Parfois je me demande si on a les bonnes définitions, pour Pi, ou pour ce qu'est un nombre premier. Je veux dire que si on trouvait une autre définition cela amènerait d'autres concepts.
C'est ce que je regrette avec les souris et l'informatique, on n'est plus dans le concret. Quand on a un compas dans les mains c'est autre chose que de programmer le tracé d'un cercle sur un ordinateur.
Dans la nature il y a beaucoup de spirales plus que de cercles. Le cercle n'est qu'une spirale particulière.
Sur la mémoire de Pi j'avais posté ça : https://www.zebrascrossing.net/t6144p450-ne-vous-y-fiez-pas#1615950
@ProfDeLettres : Oui c'est certain, l'infini, c'est énorme. Un point autrement intéressant est la question du passage aux limites.
Parfois je me demande si on a les bonnes définitions, pour Pi, ou pour ce qu'est un nombre premier. Je veux dire que si on trouvait une autre définition cela amènerait d'autres concepts.
C'est ce que je regrette avec les souris et l'informatique, on n'est plus dans le concret. Quand on a un compas dans les mains c'est autre chose que de programmer le tracé d'un cercle sur un ordinateur.
Dans la nature il y a beaucoup de spirales plus que de cercles. Le cercle n'est qu'une spirale particulière.
Sur la mémoire de Pi j'avais posté ça : https://www.zebrascrossing.net/t6144p450-ne-vous-y-fiez-pas#1615950
Dernière édition par siamois93 le Mer 30 Oct 2019 - 15:50, édité 1 fois
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
hobb a écrit:ProfDeLettres a écrit:C'est un record comme un autre ceci dit. Mais à quoi servent les records ? A la satisfaction de l'ego ? ;-)
Aux outils à mettre en oeuvre, à l'avancée technique et scientifique pour atteindre de tels niveaux ;-)
J'aurai dit bêtement un moyen de comparer la vitesse d'exécution de deux ordinateurs.
Ou à se représenter une surface de 10 chiffres, 100, etc. un million comme ici : https://www.piday.org/million/

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
On a autant de précision pour d'autres constantes ou c 'est de loin la plus calculable ?
Dans des calculs scientifiques, de quelle précision a-t-on réellement besoin ?
Dans des calculs scientifiques, de quelle précision a-t-on réellement besoin ?
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
siamois93 a écrit:On a autant de précision pour d'autres constantes ou c 'est de loin la plus calculable ?
Quelles constantes ?
siamois93 a écrit:
Dans des calculs scientifiques, de quelle précision a-t-on réellement besoin ?
Ca dépend, et c'est vraiment pas simple... Ca dépend s'il s'agit de systèmes chaotiques, et si on veut uniquement une analyse statistique, ou bien descriptive, et du système à résoudre, et des ordres de grandeur en présence...
Mais en général on fait tout en double précision.
Invité- Invité

ortolan- Messages : 13579
Date d'inscription : 31/07/2016
Localisation : 404 Not Found
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
D'où la question : comparées à quelles constantes (il y en a un sacré paquet... 2 aussi est une constante, qui apparait partout, et qu'on sait bien calculer ^^)
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Il y a des techniques similaires oui... enfin après c'est vrai que la course aux décimales de pi fait plus parler d'elle que de e ou autre...
Invité- Invité
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
J'ai retrouvé un turc...

Stegos- Messages : 4567
Date d'inscription : 18/02/2018
Age : 105
Localisation : 3ème planète autour du soleil
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Je l'avais déjà vue, l'animation est super sympa (j'ai bien aimé le slow motion replay)
 Re: Pour les amateurs de Pi
Re: Pour les amateurs de Pi
Après recherche il s'agit de la formule de Viète. Mais calculée ici dans un repère cartésien et non uniquement avec Pythagore. Le calcul avec Pythagore donne un résultat plus concis.
(ex ProfDeLettres)
(ex ProfDeLettres)
Invité- Invité
 Sujets similaires
Sujets similaires» Olivier pour certains, ou Mirab's pour d'autre, ou encore Graal pour les plus intimes
» Mon univers - tome II
» Publicité pour un nouveau groupe facebook créé par des zèbres pour pas seulement pour les zèbres "Led Zepponge"
» Publicité pour un nouveau groupe facebook créé par des zèbres pour pas seulement pour les zèbres "Led Zepponge"
» Publicité pour un nouveau groupe facebook créé par des zèbres pour pas seulement pour les zèbres "Led Zepponge"
» Mon univers - tome II
» Publicité pour un nouveau groupe facebook créé par des zèbres pour pas seulement pour les zèbres "Led Zepponge"
» Publicité pour un nouveau groupe facebook créé par des zèbres pour pas seulement pour les zèbres "Led Zepponge"
» Publicité pour un nouveau groupe facebook créé par des zèbres pour pas seulement pour les zèbres "Led Zepponge"
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Évènements
Évènements