Solfège et théorie musicale

L'approche anglo-saxonne est beaucoup plus logique et ludique que les méthodes classiques.
Faudrait trouver une méthode adaptée a la guitare sans trop de parlotte.
Quoiqu'il en soit le solfège n'a rien de bien sorcier, la flûte au collège et les ecole de musique aux profs acariâtres on traumatisé toute une population...

SiOOL a écrit:Faudrait trouver une méthode adaptée a la guitare sans trop de parlotte.

Le solfège est le nommage, l'écriture et la lecture de la musique. Pour la lecture spécifiquement sur la guitare, il existe des tas de méthodes, mais je pense qu'en ce qui concerne la guitare moderne, typiquement électrique, et jouée au médiator, la méthode de référence est A Modern Method for Guitar, de William Leavitt, enseignée à Berklee (qu'il faudrait vraiment que je me finisse un de ces 4, j'ai honte de laisser traîner ça depuis si longtemps... L'année prochaine, après mon déménagement, je me la plie ! )

oui leavitt c'est très bien c'était à ça que je pensais.

pour la lecture à vue, faut farmer du standard dans premier temps puis aller vers des trucs plus velu mais faut en avoir l'utilité, de la lecture à vue.

SiOOL a écrit:mais faut en avoir l'utilité, de la lecture à vue.

Absolument ! Autant apprendre ses notes sur son manche et être capable de lire (pas à vue) un thème fait partie des compétences nécessaires du musicien rythmique/soliste/improvisateur/compositeur/..., autant lire à vue sur un instrument aussi difficile que la gratte, c'est vraiment si on en a une nécessité absolue, vu le nombre de doigtés possibles pour n'importe quelle séquence de notes ! Ça me rappelle une interview de Steve Vai qui disait qu'un été il avait décidé de dédié ses deux mois à plein temps à devenir un super lecteur à vue. Il était revenu au mieux médiocre lecteur à vue. Quand on connaît le loustic, on mesure l'étendue de la tâche...

Un article sur les gammes, la notion de tension/résolution (vers 1/4 de la page)
https://composer-sa-musique.fr/les-differents-types-de-gammes-mineures/

Je ne sais pas ce qu'il vaut (lu en diagonale pour un autre truc sur les gammes) mais de loin ça a l'air intéressant.

Parmi les choses qui sont bien coincées de mon côté, si quelqu'un a quelques minutes pour développer svp.
Quand on dit que "quelque chose" est par exemple en "La mineur"

1. Est-ce que cela signifie que le compositeur a uniquement pioché dans la gamme correspondante ?
   
2. Est-ce que c'est sous entendu que c'est la mesure jusqu'à ce qu'on précise autre chose (un peu comme la time signature), ou alors ça ne peut que figer l'harmonie dans le morceau entier (dans ce cas pourquoi) ?
   
3. Quel est le but de cette précision ? Aider les interprètes à choisir un doigté au piano ou une position à la guitare par exemple ?
   

Si vous avez des exemples aussi ou des lectures à recommander, je prends
Pour situer ma compréhension actuelle de tout ça, la seule chose à laquelle j'ai pu me raccrocher pour l'instant se trouve dans ce message (penta mineure de Mi).

Une vidéo que j'ai trouvée très bien faite autour des rythmes :

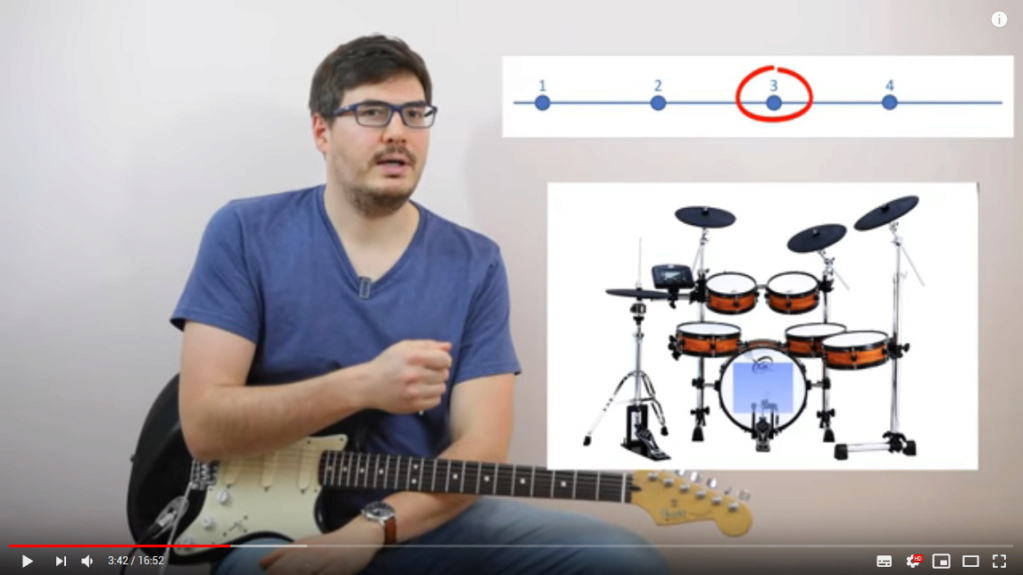
Comprendre le rythme à la guitare binaire, ternaire, contretemps, croches, etc:

Il y a un rappel mesures/temps, la relation avec la batterie (avec exemple classique : grosse caisse sur temps 1 et 3, caisse claire sur 2 et 4 + temps/contretemps si on joue hors batterie), des exemples concrets dans différents styles (pour les bassites, il simule la partie basse sur les temps dans un genre particulier où le guitariste est calé sur les contre-temps), et des schémas dynamiques genre ça.

stv82 a écrit:Quand on dit que "quelque chose" est par exemple en "La mineur"
Est-ce que cela signifie que le compositeur a uniquement pioché dans la gamme correspondante ?

En gros, même s'il a probablement modulé par endroits, ou peut-être approché certaines notes cible chromatiquement. Ça ne change pas l'idée générale. Stricto sensu, c'est incomplet, il faudrait spécifier mélodique, harmonique ou naturel (contrairement au majeur). En tout cas, tu as de grande chance de finir le morceau sur une résolution, donc sur un accord de la mineur.

stv82 a écrit:Est-ce que c'est sous entendu que c'est la mesure jusqu'à ce qu'on précise autre chose (un peu comme la time signature), ou alors ça ne peut que figer l'harmonie dans le morceau entier (dans ce cas pourquoi) ?

Ce peut être le morceau, un passage... C'est spécifié ("morceau en la mineur", ou bien "le pont est en la mineur", "à la huitième mesure on module en la mineur jusqu'à la douzième", etc.)

stv82 a écrit:Quel est le but de cette précision ? Aider les interprètes à choisir un doigté au piano ou une position à la guitare par exemple ?

Le but, c'est de comprendre la musique. En général, on ne fait pas l'analyse pour toi, c'est à toi de savoir comment tu comprends la grille et la mélodie, pas plus que tu n'as un prof de français avec toi ou une dissertation d'analyse fournie à chaque fois que tu lis un bouquin ou regarde un film. Si on te fait une analyse (dont l'expression de la tonalité est le début du commencement de l'amorce du démarrage), c'est pour t'aider à mieux comprendre, à improviser, à ajouter des accords, à ajouter des extensions à ceux existant, ou simplement à te familiariser avec la langue que tu es en train d'apprendre. Incidemment, si tu n'avais pas reconnu ce que tu étais en train de jouer, ça peut toujours t'aider à retrouver les doigtés de la gamme,  en effet.

Merci AcideMatt,

J'en profite pour revenir sur une grosse confusion que je me trimballais sur les notions échelle / mode / gamme / degré.
J'ai l'impression que ça s'est éclairci aujourd'hui. Espérons que c'est bien le cas

Différence échelle / mode / gamme / degré

Échelle

Une échelle est une façon de monter un escalier d'intervalle menant de note en note.
Par exemple, ton - ton - 1/2 ton - ton - ton - ton - 1/2 ton

Mode

Un mode définit une classe de gammes caractérisées par une échelle d'intervalles donnée.
Ainsi le mode majeur définit une classe de gammes diatoniques caractérisées par les intervalles suivants : ton - ton - 1/2 ton - ton - ton - ton - 1/2 ton

On peut voir les modes comme des masques à appliquer sur une note de départ pour obtenir une gamme. Évoqués sans note de départ, ils définissent donc des classes de gammes (leur caractéristique commune au sein de la classe étant la composition de la séquence d'intervalles séparant les notes entre elles).

Ce sont eux qui donne une coloration à la musique comme ce sont eux qui définissent les séquences d'intervalles. Peu de gens ont l'oreille absolue, donc beaucoup ne repèrent en fait que les différences entre les tons, donc les intervalles, peu importe la note de départ et les notes constituantes. Personnellement, à la basse, je décale souvent un riff ailleurs sur le manche. Je vois que les notes sont différentes mais je reconnais bien le morceau car les intervalles jouées sont bons même si les notes officielles ne le sont pas.

Si je ne me goure pas, ce sont donc les modes qui sont super importants à comprendre et pas les gammes car elles découlent.
La gamme n'étant que l'instanciation du masque de mode à partir d'une note de départ.

Gamme

Une gamme est le résultat de l'instanciation d'un masque de mode à une note donnée (appelée tonique). Cela donne donc un ensemble de notes atteintes par la séquence d'intervalles du mode.
Par exemple, si on applique le mode ionien à la note de Do, on obtient la gamme de Do majeure: Do Ré Mi Fa Sol La Si Do

Degré

Maintenant si on part d'une note donnée, on va retomber sur une note à l'octave du dessus à la fin de cette séquence. Comme c'est cyclique,
on aime bien représenter cela sous forme d'un cercle.

Exemple en partant de Do



Et comme on tourne dans un cercle, on appelle les différentes marques atteintes des degrés.
Et on a donné des petits noms pour bien se repérer de l'intervalle qui nous intéresse

Code:

| *chiffrage* | *degré de l'échelle* | *nom du degré gamme majeure* |
|           1 | 1er / I              | tonique                      |
|           2 | 2ème / II            | sus-tonique                  |
|           3 | 3ème / III           | médiante                     |
|           4 | 4ème / IV            | sous-dominante               |
|           5 | 5ème / V             | dominante                    |
|           6 | 6ème / VI            | sus-dominante                |
|           7 | 7ème / VII           | sensible                     |
|-------------+----------------------+------------------------------|
|           8 | 8ème / VIII          | octave/tonique               |


Attention:

• Ces "degrés" mesurent des "angles" variables, au contraire des mesures d'angle habituelles du cercle trigo (degrés 0-360).
  
• C'est plus facile d'avoir un schéma avec des notes mais ce qui caractérise les degrés ce sont bien les modes
  

Quelle confusion est-elle possible ?

Alors pour ma part, le mélange s'opéraient surtout entre les modes et les gammes.
La faute à ça :

Code:

| *Degré* | *Nom moderne* | *Nom courant*   | *Séquence d'intervalles en tons* |
| I.      | Mode de do    | Mode ionien     | 1 - 1 - 1/2 - 1 - 1 - 1 - 1/2    |
| II.     | Mode de ré    | Mode dorien     | 1 - 1/2 - 1 - 1 - 1 - 1/2 - 1    |
| III.    | Mode de mi    | Mode phrygien   | 1/2 - 1 - 1 - 1 - 1/2 - 1 - 1    |
| IV.     | Mode de fa    | Mode lydien     | 1 - 1 - 1 - 1/2 - 1 - 1 - 1/2    |
| V.      | Mode de sol   | Mode mixolydien | 1 - 1 - 1/2 - 1 - 1 - 1/2 - 1    |
| VI.     | Mode de la    | Mode éolien     | 1 - 1/2 - 1 - 1 - 1/2 - 1 - 1    |
| VII.    | Mode de si    | Mode locrien    | 1/2 - 1 - 1 - 1/2 - 1 - 1 - 1    |

Ces différents modes sont obtenus en accolant deux séquences du mode de Do puis en se décalant d'une marche à chaque fois.
Comme on part du Do, la première marche devient successivement les 7 notes de la gamme majeure

Code:

│                              │                               │
  1 - 1 - 1/2 - 1 - 1 - 1 - 1/2 - 1 - 1 - 1/2 - 1 - 1 - 1 - 1/2
      1 - 1/2 - 1 - 1 - 1 - 1/2 - 1 *= mode de ré*
          1/2 - 1 - 1 - 1 - 1/2 - 1 - 1 *= mode de mi*
                1 - 1 - 1 - 1/2 - 1 - 1 - 1/2 *= mode de fa*
                    1 - 1 - 1/2 - 1 - 1 - 1/2 - 1 *= mode de sol*
                        1 - 1/2 - 1 - 1 - 1/2 - 1 - 1 *= mode de la*
                            1/2 - 1 - 1 - 1/2 - 1 - 1 - 1 *= mode de si*


Mais là attention, ce n'est pas parce que c'est un mode de La qu'une gamme correspondante doit commencer par La.
C'est juste l'intérêt du mode : on prend le masque et on le pose sur une note de départ, peu importe laquelle, et cela génère une gamme.
Mais c'est plutôt le mode auquel on est sensible.

Personnellement, je vais essayer de parler plutôt avec le nom grec du mode et bien garder en tête qu'un mode est un masque.
Ça m'évitera de me mélanger les pinceaux.

Ça aurait été l'occasion aussi d'apprendre que les sonorités orientales utilisent en fait des échelles avec des 1/4 et 3/4 de tons !
On peut s'en approcher avec ce pseudo mode oriental : 1/2 ton - 3/2 tons - 1/2 ton - 1 ton - 1/2 ton - 3/2 tons - 1/2 ton

Oui et une interrogation qui m'avait intrigué avec les modes et qui n'est pas forcément bien rendue dans le message ci-dessus.

Si on parcourt les mêmes notes dans les différents modes, à quoi ça sert d'avoir 7 modes comme on ne pourra piocher que dans les mêmes notes ?
Je veux dire OK les intervalles sont différents mais on rejoint les mêmes notes, c'est toujours "Do Ré Mi Fa Sol La Si"

En fait la tonique est super importante pour se défaire de ce raccourci, et il faut bien raisonner avec la tonique + l'échelle d'intervalles.

Le guitariste l'évoque dans cette vidéo sur le mode phrygien = mode de Mi, et précise l'importance de la tonique :

https://youtu.be/8TumuTnx_Wc?t=36 a écrit:
On peut être confondu un peu et c'est sûr on peut se dire "mais c'est les mêmes notes donc pourquoi j'appelle pas ça Do majeur"
Simplement parce que si j'ai donc le "Do" et le "Do" est la note principale, mon oreille va percevoir le "Do" comme la note principale
Et c'est ce qu'on appelle la tonique

Voilà si je joue la gamme de "Do"
"Do" va nous sembler être la note principale est là, j'ai généré la gamme majeur

Mais si je commence avec une autre note et l'autre note devient la note principale en fait, mon oreille va percevoir cette gamme tout à fait différemment
Si justement j'ai Mi et là j'ai cet accord oui maintenant toute la gamme sonne complètement différemment
Un peu espagnol aussi un peu

Et donc à ce moment-là j'ai généré ce troisième mode
"Mi" maintenant à notre oreille semble la note principale et si je commence ce troisième mode
Donc à partir "Mi" pour ce troisième mode
J'aurai tout à fait une autre perception
Et le troisième mode en fait tu vas avoir une structure différente puisque là maintenant je commence
J'ai un demi-ton directement ce que je n'avais pas en fait quand je jouais la gamme majeur
Donc là on a Mi Fa (1/2 ton) puis Fa Sol (1 ton), Sol La (1 ton), La Si (1 ton), Si Do (1/2 ton), Do Ré (1 ton) et Ré Mi (1 ton)

On appelle cette gamme donc le mode phrygien
C'est une gamme mineure

Notez au passage l'avant dernière phrase "On appelle cette gamme donc le mode phrygien".
Allez-y mollo, déjà que j’entrave que dalle !
Je dirais "Cette gamme est donc générée avec le mode phrygien à partir de telle tonique"

Bon sinon en plus, il y aurait aussi cet article qui liste les modes et donne des fichiers sonores pour se rendre compte
https://fr.wikipedia.org/wiki/Liste_des_%C3%A9chelles,_des_gammes_et_des_modes

Attention, il y a un encart rouge qui laisserait entendre que le contenu n'est pas top. En tout cas, on se rend bien compte de l'importance de la tonique, et si on prend le ionien et le dorien, on pioche dans les notes "habituelles" de l'occidental moyen "Do Ré Mi Fa Sol La Si" et pourtant c'est vachement perturbant
https://fr.wikipedia.org/wiki/Liste_des_%C3%A9chelles,_des_gammes_et_des_modes#Terminologie_moderne

Cette chaine avait déjà été évoquée plus haut.
Personnellement, je pique du nez sévère à l'écoute mais si on arrive à tenir c'est vraiment bien expliqué.
Ici les accords et les renversements : https://youtu.be/3v2vTRupzgA?list=PLyIR6Ix26WY9lELxy0dpDOpjfmYLTGsHA&t=934

Et un résumé ci-dessous, notamment la fin avec un exemple d'analyse.

État fondamental d'un accord

Code:

5  (sol)
3  (mi)
F  (do)

Par exemple, do-mi-sol avec le do = F
La fondamentale donne son nom à l'accord
Le chiffre complet serait

Code:

5
3

Le chiffrage conventionnel est en fait

Code:

5 ou rien

État de 1er renversement d'un accord

Ensuite, si on commence par un mi, ce n'est pas forcément un accord de mi ! Ça peut être un accord de do mais avec un Do plus aigu
Donc sur une portée, le do est au dessous des 2 autres
Cela devrait donner ceci

Code:

F  (do, octave +1)

5  (sol)
3  (mi)

Mais comme on part de l'ancien 3, on ne peut plus le chiffrer 3 en premier ! Il devient la "Basse"

Code:

6     (do, octave +1)
3     (sol)
Basse (mi)

Quand il y a un chiffrage pair, c'est le signe d'un renversement
C'est le premier renversement mi-sol-do
Le do qui est en bas a disparu
L'accord est un peu flottant, il n'a pas d'assise sur sa fondamentale.
Il n'est plus à l'état fondamental mais à l'état de 1er renversement.

Le chiffrage conventionnel est plus ramassé : 6
Mais quand on voit 6, cela veut dire en fait 3 et 6

État de 2nd renversement d'un accord

Ensuite, on recommence avec l'ancien 5 du démarrage ie. sol
Donc sur une portée, le do est au dessous du sol et le mi au dessus du do. Cela devrait donner ceci

Code:


3  (mi, octave +1)
F  (do, octave +1)

5  (sol)

Mais comme on part de l'ancien 5, on ne peut plus le chiffrer 5 en premier ! Il devient la "Basse"

Code:

6      (mi, octave +1)
4      (do, octave +1)
Basse  (sol)

Comme les deux chiffres sont pairs, l'accord est complètement renversé
Le chiffrage conventionnel est égal au complet : 6 4

C'est le deuxième renversement sol-do-mi

Pour conclure,
- À l'état fondamental, la fondamentale est à la basse
- À l'état de premier renversement, c'est l'ancienne tierce de l'accord qui est à la basse. Mais ce plus une tierce, c'est une basse. Elle ne mérite aucun titre d'intervalle.
- À l'état de second renversement, c'est l'ancienne quinte de l'accord qui est à la basse. Mais ce plus une quinte, c'est une basse.

Analyse d'un accord

Analyse de quelques notes en haut à gauche (sur les 2 portées clés sol + fa)


On a ces notes

Code:


          do
clé sol   sol
          do

          sol
clé fa    mi

          mi grave

1. IDENTIFICATION DE L'ACCORD
  de quel accord s'agit-il ?
  on part du bas = mi, puis on voit sol et do donc s'agit-il d'un accord de mi, de sol ou de do ?
  - si c'est un accord de mi, je dois trouver mi-sol-si
     hors pas de si, donc pas accord de mi
  - si c'était un accord de sol, j'aurais sol-si-ré
    hors pas de ré, donc pas accord de sol
  - pour l'accord de do, do-mi-sol, c'est bien lui
  C'est un accord de *Do majeur*
2. une fois l'accord déterminé, quel est son état ?
  c'est la basse, la note la plus grave qui va nous le dire
  ici c'est un mi donc c'est un accord de premier renversement
  on le chiffre donc 6

Pour tous ceux qui seraient restés sur le carreau avec la terminologie musicale (ses termes qui veulent dire pareil mais en fait pas à tout à fait), la construction des accords par empilement (ce n'est plus consonant, c'est pas grave allez, youpi), la différence musique tonale/modale, l'harmonisation des échelles etc. je recommanderais bien l'auteur Serge Donval.

Je suis en train de lire en particulier : Histoire universelle de la musique et de la théorie musicale.
Il y a un résumé de certaines notions abordées ici http://donvalmusicalacoustics.org/indexFR.html

Voici quelques trucs qui m'ont causé, dont les annexes !

chimère accord parfait majeur et construction des accords

Voir [[musique harmonique]]

Le problème qui envenime la musique occidentale depuis la Renaissance) est que si l'intervalle de quinte (Do-Sol) est harmonieux, celui de 3ème majeure (Do-Mi) ne l'est pas vraiment.

Il l'était un peu à la période baroque (accordage non uniforme, tons pas égaux)

Depuis l'uniformisation a conduit à une tierce majeure un peu plus élevée que la tierce harmonique. Cela n'a pas empêché de bâtir toute la musique occidentale sur cette notion d'accord parfait (majeur) chimérique

Attention la tierce actuelle n'est pas consonante en fait.
- Consonances parfaites : unisson, quinte et octave
- Consonance imparfaites (admises) : tierce et sixte
- Dissonances : tout le reste (y compris la quarte)

1 Le Tonal et le Modal

Dans cette première annexe nous allons essayer de mettre un peu d'ordre
en matière de terminologie car la confusion règne entre les 7 termes de la
théorie musicale occidentale : Mode, Gamme, Échelle, Modalité, Tonalité,
Tempérament, et Système. Les 3 premiers ont déjà été définis dès le premier
chapitre, cela n'empêche pas de les confondre mais l'arrivée des autres peut
tout remettre en cause.

  Le terme « Mode » est le plus simple, et le plus universel, ou du moins il
doit l'être. Il signifie un modèle, un schéma, par exemple :

- majeur : T, T, 1/2, T, T, T, 1/2
- mineur (antique) : T, 1/2, T, T, 1/2, T, T
- phrygien : 1/2, T, T, T, 1/2, T, T
- rast : T, 3/4, 3/4, T, T, 3/4, 3/4
- hijaz/tzigane/andalou : 1/2, 3/2, 1/2, T, 1/2, T, T


 « Echelle » indique une suite de notes ou de degrés dont l'écart (ou le pas)
n'est pas obligatoirement régulier. Il existe des échelles de type
pentatonique, heptatonique, duodécimale à 12 degrés, micro-tonales à 19 ou
24 notes, pour ne citer que les plus courantes. Le terme « Echelle » est
parfois employé avec des sens légèrement différents. On peut le confondre
avec « Gamme » ou « Tempérament ».

 « Gamme » est un terme très général. Il est purement latinique
équivalent chez les anglo-saxons, « garnut », est d'un emploi rare. Son sens
est plutôt flou, il remplace souvent les précédents, et en particulier « mode »
A priori, on peut penser qu'il provient de la langue courante (gamme de
produits ou d'articles) mais sa vraie origine est musicale. Gamma (comme
dans la notation anglo-saxonne : C, D, E, F, G. ...) désignait la note Sol qui
servait de référence (clé de Sol, solfège et solmisation).
« Tempérament » : Vers la fin de la Renaissance, on a extrapolé l'échelle
musicale heptatonique en continuant le Cycle des Quintes, (chap. N.5) vers
le haut (et vers le bas) pour obtenir les notes diésées (et les notes
bémolisées). Et pour répondre aux impératifs de l'Intonation Juste (avec un
Mi naturel, s-chap. V.5 et V.6), on se retrouve avec des notes diésées et
bémolisées non enharmoniques (par exemple : Sol# différente de Lab), et un
total de 19 notes. Au cours du 17è'" siècle, on les a réduites progressivement
à 12. Ces 12 demi-tons sont aujourd'hui rigoureusement égaux mais ils ne
l'étaient pas pendant l'époque baroque. Plusieurs théoriciens et musiciens
ont proposé des accordages différents à partir du modèle méso-tonique, mais
vers la 1 ère moitié du 1 re siècle les interprètes accordaient leurs claviers à
leur goût (s-chap. VI.7). Le Tempérament est donc la manière d'accorder les
notes de l'échelle musicale, d'où le terme anglais « Tuning », cela revient
implicitement à déterminer la fréquence (ou le pitch) de chacune des 12
notes.
Chez les anglo-saxons, « Temperament » se confond parfois avec
« Echelle » (Scale) quand celle-ci désigne, dans le cas général, toute
division de l'octave en un nombre de notes. On dit Tempérament à 19, à 24
ou à 31 degrés.
« Système » est utilisé principalement dans la littérature anglo-saxonne, il
équivaut à Tempérament et à Echelle.
« Tonalité » est presque l'équivalent de « mode », en mettant la tonique en
exergue; on parle alors de tonalité de Do majeur ou de La mineur. Cela
paraît simple, mais une mélodie n'est pas seulement une suite de notes
appartenant à un mode bien défini, et se terminant par la tonique. Sinon, où
est la musique en tant que « art de combiner les sons d'une manière agréable
à l'oreille ». Les principaux critères de la musicalité sont :

* l'Intonation : succession de moments forts/tendus et d'autres
calmes/reposants (ponctués par des arrêts plus ou moins longs).

* la Hiérarchie des degrés participe à l'Intonation : après la tonique, c'est la
dominante qui détient le second rôle. Une phrase commence souvent par la
dominante en anacrouse, et se termine par la tonique (ou l'octave) parfois
précédée de la dominante.

* la Cadence (chap. 11.5), conclusive ou suspensive, existe sous différentes
formes dans la musique monodique/mélodique (chants traditionnels par
exemple).

Ces éléments sont respectés par les musiciens amateurs même ceux qui
n'ont jamais été sur les bancs d'un conservatoire, et (le comble !) par les
musiciens de toutes les autres cultures. C'est cela la Tonalité, elle n'est pas
l'apanage de la musique occidentale harmonique mais elle peut-être
renforcée par l'Harmonie et l'enchaînement des accords. C'est un langage
universel, exploité aussi, bien en Occident qu'en Orient, et est toujours en
vigueur en ce début de 3eème millénaire (chap. VI.1).

Ce concept d'Intonation était absent (ou très faible) dans le Plain-chant
grégorien (d'ailleurs plain signifie uniforme/uni, comme « plain » en
anglais), mais il était présent dans les chants populaires et dans les oeuvres
des ménestrels de tous bords.

« Modalité » : Les musicologues contemporains considèrent que la fin de
la Renaissance (les années 1600) comme une date décisive dans l'évolution
chronologique de la théorie musicale. Pour eux, depuis cette date c'est la
« Tonalité », et avant c'était la « Modalité » (il fallait bien trouver un nom).
On confond très souvent dans la littérature « Modalité » et « Musique
mélodique/monodique » (non harmonique, mais pourtant tonale, comme
celle d'Orient).

D'après S. Gut, « D'une manière générale, on peut parler de tonalité élargie
pour toute musique qui s'organise autour d'un son ou d'un groupe de sons
servant de pôle d'attraction, on rejoint par là le sens allemand du mot  Tonalitât »
« qui englobe aussi bien le tonal que le modal ». Le
Dictionnaire Vignal [5], lui, parle de « Tonalité Généralisée » qui n'est pas
restrictive à la musique harmonique et à la dichotomie majeur-mineur (qui
nous rappelle la philosophie du Yang et du Ying de l'Extrême-Orient). Voir
« La musique modale en France de Berlioz à Debussy » de Henry Gonnard.

2 Eléments d'Acoustique

La Cadence / Les Battements

Comme nous l'avons expliqué au sous-chapitre 11.5, la meilleure manière
de conclure une phrase musicale est l'accord parfait précédé de l'accord de
7ème de dominante. L'accord parfait est constitué des degrés les plus
consonants : octave, quinte et tierce. L'octave et la Quinte sont des
consonances parfaites, et figurent toujours dans le dernier accord (la tierce
est généralement renvoyée en 10ème ou 17ème position).

La dissonance est le résultat du cumul de plusieurs facteurs, et leur étude
fait appel à des notions d'Acoustique (une branche des Sciences Physiques)
que nous évitons d'étaler ici mais que nous avons déjà expliquées dans notre
premier ouvrage.

Les sons partiels harmoniques (s-chap. 11.2) sont accusés d'être le suspect
n°1 :
- quand les 2 notes extrêmes d'un intervalle (Do et Sol, par exemple) ont
des harmoniques qui coïncident, le résultat est agréable
- quand ils sont disparates comme dans le cas de Do et Fa, l'onde sonore
globale est perturbée et l'impression sur l'oreille est mauvaise.

Les battements ([1] 11.5) représentent eux aussi une cause importante.
Quand on exécute 2 sons très proches le résultat n'est pas très agréable, pas
très net, il contient des battements. On observe ce phénomène en grattant 2
cordes qui ne sont pas très bien accordées, et en les accordant on supprime
ce phénomène désagréable. Cela revient à dire que plus les 2 fréquences
s'approchent, plus les battements diminuent jusqu'à disparaître quand les 2
sons sont confondus (enharmoniques).

Pour conclure une phrase (en mélodie/monodie), la 7ème majeure (ou la
sensible) précède très souvent l'octave (ou la tonique), elle est à un demi-ton
en-dessous et l'écart de leurs fréquences est inférieur à 10 %. L'octave (ainsi
que la tonique) étant toujours présente à l'esprit, la sensible crée des
battements sonores que seule l'octave peut faire disparaître. C'est
l'explication de « l'attraction » de la sensible (« leading note » chez les
anglo-saxons) vers l'octave.

En Harmonie, on préconise (s-chap. 11.5) par ailleurs le mouvement
conjoint : Ré => Do ou Mi. L'écart est alors d'un ton, environ 12 %, et le
raisonnement précédent reste valable. Voilà l'explication, par des arguments
acoustiques, de la Cadence Parfaite, passage de l'accord de 7ème de
dominante à l'accord parfait de tonique (le cas de Sol=>Sol ou Sol=>Do
peut être expliqué d'une manière similaire).




L'absurdité du Renversement

D'après S. Caron : « Un accord à l'état fondamental est tonalement plus
affirmé qu'un accord au premier renversement », et il est encore plus
dénaturé au deuxième renversement qui « ne doit être employé qu'avec
certaines précautions, dont la préparation et la résolution de la quarte [Sol-
Do] » d'après Th. Dubois.

Un accord majeur est bâti sur la consonance des harmoniques : la quinte
(3/2) et la tierce (5/4), cette dernière étant légèrement déformée (décalée vers
le haut) sur le clavier actuel mais ce sont d'authentiques harmoniques. La
tierce mineure (6/5) ne fait pas partie des harmoniques mais elle est
reconnue à l'unanimité par sa douceur et donne un accord plutôt agréable.

Si on renverse l'accord majeur, on obtient Mi-Sol-Do. L'intervalle Mi-Do
est une sixte mineure (8/5) qui n'est pas vraiment harmonieuse. Si on
renverse une deuxième fois, le résultat est Sol-Do-Mi, et on a alors une
quarte Sol-Do vraiment dissonante.

La technique du renversement a été introduite du temps de la Basse
Continue au début du 17ème siècle pour deux motifs pragmatiques et non
acoustiques.

1) Cela facilitait le jeu de la Basse : on pouvait accompagner la voix
  supérieure en exécutant la voix basse au moyen des 3 notes (dans n'importe
  quel ordre) de l'accord.
2) Lors de l'écriture cela laissait au compositeur le choix entre 3 notes
  pour avoir des lignes bien mélodieuses (cf. Règles du Contrepoint, s-chap.
11.4). Les théoriciens ont essayé, a posteriori, de justifier cette technique
mais leurs arguments ne sont pas convaincants. Rameau a rédigé plusieurs
ouvrages sur l'harmonie, et était un fervent défenseur de l'écriture verticale
(au détriment de l'esthétique mélodique horizontale), c'était l'objet (ou la
cause) de ses controverses avec Rousseau. Pour Rameau « la basse
fondamentale à son tour est produite par le concours des sons
harmoniques ». Cela veut dire que si on joue Mi-Sol-Do ou Sol-Do-Mi le
fondamental (grave) Do sera reconstitué, malheureusement nos calculs ([1]
chap. XIX) ne confirment pas ce constat.


Mesure d'Intervalle

Dès le premier chapitre (s-chap. 6) nous avons été amenés à employer le
« cent » pour évaluer la taille (ou la mesure) d'un intervalle (il y aussi le
« savart »). Il faut retenir surtout que l'octave vaut 1200 cents, et que chaque
demi-ton (diatonique ou chromatique) du clavier moderne vaut 100
cents (cela donne 500 pour la quarte et 700 pour la quinte).

Nous sommes obligés de faire appel à quelques formules mathématiques
que le lecteur risque de ne pas comprendre ou apprécier, mais il peut quand
même les utiliser (avec l'aide d'une calculette) pour évaluer n'importe quel
intervalle (par exemple la tierce harmonique 5/4, ou la tierce majeure
pythagoricienne 81/64 provenant du Cycle des Quintes).
Vers 1700, le physicien français Savart a adopté une formule simple :

          I = 1000 x log10 f2/fi


Elle donne pour l'octave 301 savarts (symbole : cy, sigma), en omettant les
décimales (chiffres après la virgule).

Vers le milieu du 19ème siècle, lorsque le Tempérament Egal s'est
généralisé, l'anglais Ellis a établi une formule qui convient mieux à cette
situation. Avec une échelle contenant 12 degrés, il a assigné à chaque degré
la valeur d'une unité, c'est-à-dire 100 cents (cent signifie centième chez les
anglo-saxons). La formule mathématique qui résulte de ces considérations
est alors :

1200 x log2(f2/fi)
1200 x [log10(f2/fi)/log10(2)]

3 La Quarte entre Consonance et Dissonance

I, IV, V; ce sont les fameuses notes tonales. Elles ont fait du chemin,  
depuis qu'un obscur personnage de la fin de l'Antiquité romaine a élaboré la  
notion de rapports épimores (super-partiels). C'est l'archétype du théoricien-
spéculateur qui n'a jamais rien composé (et sans doute il n'a jamais fait de  
musique). Par contre il était philosophe, théologien, et consul; il a écrit des  
livres, et a fait de la politique (ce qui lui a coûté la tête). Après le grand vide  
du haut Moyen-âge (d'environ 5 siècles), la Polyphonie a fait ses premiers
pas en se basant sur les degrés censés être les plus consonants, les 4e et 5  
degrés qui ont acquis une légitimité historique. C'est la théorie des rapports  
épimores (s-chap. IV.4) qui préconise que les degrés les plus consonants sont  
de la forme (n+1) / n : 2/1, 3/2, 4/3, 5/4, etc. Et D'Arezzo a confirmé  
l'importance de ces 3 degrés (I, IV, V) dans sa théorie de l'Hexacorde (chap.  
III). Mais la Consonance est un phénomène directement lié aux  
harmoniques, nous invitons donc le lecteur à se reporter au chapitre II  
« Harmonie et Contrepoint » (11.2).

Comme nous l'avons largement expliqué dans ce chapitre II, les notes dites  
tonales (I, IV, V) sont les piliers de l'Harmonie classique. Du temps de  
l'Organum, on rajoutait une voix organale à la voix principale, à un écart de  
quinte ou de quarte, ces 2 intervalles étant considérés comme les plus  
consonants (après l'unisson et l'octave). Cette idée a bien été appliquée  
pendant l'évolution de la Polyphonie au 13ème siècle(Ars Antigua). Mais au  
lee siècle (Ars Nova) la quarte ne satisfaisaitp lus les musiciens et on lui a  
préféré la tierce comme consonance. L'Eglise s'en est mêlée, aux motifs de  
croyances qu'elle n'a pas justifiées (Décrétale du Pape Jean XXII de 1324).  
A partir des années 1400 c'est l'avènement de' trade 1-3-5 et l'abandon  
définitif de la quarte par les compositeurs, alors que les théoriciens s'y  
accrochaient toujours, c'est le Paradoxe de la Quarte ([1] VI1.6).
Durant le 15'1' siècle l'Intonation Juste était très en vogue (s-chap. V.5 et  
V.6), et il fallait prouver la consonance de certains degrés pour les insérer  
dans une échelle censée en contenir le maximum. En parallèle émergeait la  
vieille doctrine des rapports simples, et de préférence de forme épimore. La  
quarte se trouvait ainsi bien classée dans la série des supposées consonances  
épimores, c'est ce que continuent de proclamer nombreux théoriciens trop  
obnubilés par l'arithmétique. Elle est même parfois classée dans la série des
harmoniques (ce qui est faux), alors que depuis le 17'1" siècle des auteurs
ont confirmé la dissonance de la quarte :Descartes, Mersenne, Rousseau,
D'Alembert, Fux, etc.

Il fallait bien chercher un autre prétexte, et on l'a trouvé, c'est le
renversement :

François-Joseph Fétis, dans « La musique mise à la portée de tout le
monde », 1847, 524 pages : « Le renversement des consonances produit des
consonances; celui des dissonances engendre des dissonances ». « Quant aux
intervalles de quarte et de sixte majeure et mineure, ils ont été assimilés
grâce à de simples renversements d'intervalles déjà acquis et utilisés », Ch.
Duprez, qui classe la quarte après les 2 tierces. Bernard Bel : « La gamme
[indienne] posséderait les mêmes consonances [quintes] que celle de Zarlino
et bien sûr les quartes obtenues par renversement ». Paul Erlich : « ... the
only recognized consonances being the octave and theperfect fifth, plus of
course their inversions and extensions ».

Voici quelques citations :

- « L'intervalle de quarte 4/3 était une consonance qui posait problème.
 Elle était considérée théoriquement comme une consonance parfaite. Or
 depuis les 13ème et 14è1"e siècles, elle était dans la pratique délaissée auprofit
 des tierces ». Brigitte Van Wymeersch, « La tradition arithmétique en
 musique. L'exemple de Gassendi ».
- « Au 15ème siècle, les quartes étaient d'ailleurs devenues le désespoir des
 théoriciens », Charles Rosen, dans « Schonberg », Editions Minuit, Paris,
 1979.
- « Consonances parfaites : unisson, quinte et octave. Consonances
 imparfaites : sixte et tierce. Les intervalles restants, y compris la quarte, sont
 des dissonances. », 1725, J. J. Fux, Jean-Philippe Navarre, p81 [13].
- « Les divers statuts successifs de la 4' reflètent bien l'embarras des
 théoriciens médiévaux », p322. « Du 12ème au 14ème siècle la 4' devient
 dissonance! », Devie [17] p322.
- À partir de la Renaissance, la quarte devint une dissonance, et les
 consonances furent dites soit « parfaites » (octave et quinte), soit «
 imparfaites » (tierce et sixte) », Larousse. Rappelons le début de la
 Renaissance musicale date des années 1400.
- Au 14ème siècle : «... le changement de statut de la quarte, qui de
 Consonance est passée dans la catégorie des dissonances », «... alors que
 "intervalle arithmétiquement simple de quarte s'est vu rejeter dans la
 catégorie opposée [celle des dissonances) Coeurdevey, [9] p28.

4 Le Tempérament, ou l'évolution de l'échelle musicale

La quasi-totalité des musiciens daujourd'hui n'ont pas d'idée précise sur  
l'importance du Tempérament et de son évolution au cours de l'Histoire. Ils
n'ont connu que le « Tempérament Egal » (s ch . IV.6), standard, où tous
les demi-tons (diatoniques et chromatiques) sont égaux, et des commas qui
ont disparu à jamais (sauf dans les manuels). Le demi-ton sur le clavier
moderne est rigoureusement égal au 12ème de l'octave, cela paraît très simple
et même évident et logique. Hélas non, cette division de l'octave en 12
degrés tous égaux n'a rien d'acoustique ou d'esthétique ou de musical. J.-S.
Bach (m. 1750), le compositeur le plus cité dans cet ouvrage (et dans tous les
livres d'histoire de la musique), n'accordait pas son clavier selon le
« Tempérament Egal »; ce dernier ne s'est généralisé que vers le milieu du
19ème siècle. « C'était un moyen de fortune et non un acte idéologiquement
conscient », Wyschnegradsky [120]. L'oreille occidentale s'est habituée à
cette échelle semi-tonique, et le pire c'est qu'elle « s'est habituée à la dureté
de la tierce qui choquait l'oreille des musiciens et des facteurs de l'époque
baroque » (H. Legros, « Connaissance de l'orgue »). Nous allons reprendre
depuis le début, quitte à répéter des notions déjà évoquées aux chapitres IV
et VI.

Tout a commencé au début de la Renaissance (15ème siècle) avec Ramos
qui était le premier à instaurer la notion d'octave. Il a introduit le calcul
arithmétique pour l'évaluation des hauteurs des 12 degrés d'après la Théorie
du Cycle des Quintes (s-chap. IV.5) : limmas, commas, et apotomes.

Force est de constater que la tierce dite pythagoricienne (81/64=1,2656) de
ce Système (s-chap. IV.6) est supérieure à la tierce pure (5/4=1,25) d'un
comma, et n'est donc pas assez harmonieuse pour former un bon accord
parfait avec la tonique. Et c'est la naissance du concept d'Intonation Juste :
choix d'une échelle dont les degrés (ou du moins lesplus importants) sont
consonants avec la tonique. C'est un critère louable mais il n'est pas toujours
compatible avec les impératifs d'une échelle (comme la régularité des
intervalles, condition sine qua non pour la modulation et la transposition, et
surtout l'inviolabilité de la sacro-sainte octave, voir plus loin), en plus de la
maniabilité du clavier. Plusieurs tentatives ont eu lieu pendant environ trois
siècles et demi pour tenir compte du maximum de ces conditions, elles ont
malheureusement convergé vers la solution radicale : la plus simple certes,
mais elle est loin d'être satisfaisante cell d'une division de l'octave en 12
parties (demi-tons) égales (voir le livre de Barbour « Temperament and
Tuning » [50]).

En conclusion, jusqu'à la veille de la Renaissance il existait une échelle
qui servait aux musiciens pour composer et transcrire leurs oeuvres en
notation carrée, seulement cette échelle était mal définie du point de vue
théorique. On ignorait la notion d'octave et lelformalisme de l'Hexacorde
(s'inspirant du Tétracorde des philosophes de uéAEntiquité. grecque, s-chap.
111.4) était « bancal », et n'a jamais été appli En pratique (cela prouve
encore une fois le décalage récurrent entre thécloricien. s et praticiens), le luth,
instrument le plus répandu était étalonné selon une division égale/régulière.

Avec l'hégémonie de la Polyphonie au "1 6ème siècle, l'établissement de la
triade tonique-tierce-quinte et le problème de la tierce (majeure) pas
vraiment harmonieuse, les théoriciens de la Renaissance se sont mis à la
recherche d'un tempérament qui répond mieux aux critères de l'Intonation
Juste. Le pionnier en est Ramos de Pareja (« Musica Practica », 1482), suivi
d'Aaron et de Salinas), alors que l'Histoire a retenu surtout le nom de
Zarlino. L'échelle (ou le tempérament) de ce dernier contient des degrés
irréguliers (de 3 sortes) et cela n'est pas compatible avec la modulation et la
transposition (s-chap. V.5). Elle n'a jamais été appliquée, pourtant on en fait
l'éloge encore dans la littérature 5 siècles après sa conception.

Si on revient à l'échelle méso-tonique de P. Aaron (chap. V.6), on constate
que :

1) La succession de 3 tierces pures 5/4 est de 5/4 x 5/4 x 5/4 = 1, 953125,
la différence avec l'octave est donc 2 1, 953125 = 1,024, soit un déficit de
41 cents (presque un quart de ton) par rapport à la sacro-sainte octave.

2) La quinte méso-tonique 1,49535 avec un écart d'un quart de comma est
presque parfaite, et la suite de 11 quintes à partir de Mib aboutit à Sol#. Ces
2 notes extrêmes forment alors une quinte (ou sixte diminuée) plus grande
d'environ 37 cents que la quinte juste, elle est désagréable à l'oreille et
s'appelle « Quinte des loups » ([1] s-chap. X.3).

En conséquence, le principe du méso-tonique est attrayant, mais il crée des
« dégâts collatéraux >>. Après tout, la sauvegarde de la tierce juste peut être
négociée >>; faudrait la rehausser de nouveau un petit peu (et envisager
une diminution moins forte qu'un quart de comma sur la quinte), pour sauver
la sacro-sainte Octave. On a essayé le 1/5 de comma, il a remédié
partiellement à ce dernier problème; on a essayé le 1/6 de comma aussi. Et
quand on améliore d'un côté, on perd de l'autre; quand est-ce qu'il faut
s'arrêter ? Réponse : quand on veut. Ce n'est plus un, problème de
raisonnement acoustique, mais c'est un choix à faire. Cela dépend de chaque
musicien, le Tempérament n'est plus une science mais .un art. Dre .surcroit, les
chiffres des théoriciens c'est bien, encore faudrait-il les réaliser par un
accordeur !

Récapitulons. Nous disposons donc de 7 touches blanches-diatoniques, une
Octave parfaite en plus de 5 touches noires (Mib, Sib, Fa#, D. o# et Sol#), le
tout formant des quintes réduites chacune d une petite fraction (à
déterminer) de comma

Cette idée de baisser la quinte pure d'une fraction de comma (1/4 ou 1/5 ou
1/6) est devenue une base de travail. La tierce Do-Mi n'étant plus
parfaitement consonante, on accorde (localement) certaines tierces et pas
d'autres (voir le cercle en bas), on préserve l'octave et on n'évoque plus le
« Cycle des Quintes ». Devant ces «tâtonnements », les compositeurs et
praticiens se sont mis à accorder leurs claviers à leur goût, et selon la tonalité
de l’œuvre. Et on parle alors de « gammes tempérées », les orgues eux ont
continué l'exploitation des touches multiples (donc plus de 12) jusqu'à la fin
du 19'1" siècle (et même début 20è17e en Angleterre)

Comme exemple de « tâtonnement », le tempérament de Rameau en Do
[124] baisse d'un quart de comma 7 quintes successives, et répartit le
reliquat entre les quintes suivantes d'une manière empirique (la somme de
tous ces écarts devant être égale à -1 comma, voir Remarque du sous-
chapitre V.6).

Code:

                     Do
                Fa 0-   -1/4 Sol
                0+         -1/4
             Sib                Ré
              0+              -1/4
            Mib                  La
              0++             -1/4
             Sol#               Mi
                 0-         -1/4
                Do# -1/4 -1/4 Si
                       Fa#

Hello, il y a beaucoup de choses ici !
Je fais partie des personnes bizarres qui adorent le solfège et sont meilleures en solfège qu'en instrument. Donc si vous voulez en discuter ici ou en MP, je peux essayer de vous dédramatiser le solfège lol
Sinon, j'ai vu plusieurs références au site composer sa musique. C'est un très bon site, très bien fait pour les débutants. J'ai suivi la formation composition d'Alex et ça a été très enrichissant. Il a récemment lancé une formation solfège pour débutants, à base de vidéos et de petits exercices, si c'est comme la formation composition. C'est très clair, didactique, et bien construit.
Après, pour la lecture pure, le Dandelot et autres cités marchent effectivement très bien, mais demandent de s'y astreindre. C'est en forgeant qu'on devient forgeron !

J'ai découvert récemment toute la question du pitch.
middle C = 256 Hz ?
https://archive.schillerinstitute.com/music/rev_verdituning.html

https://waldorfmusic.org/the-relevance-of-concert-pitch/

Ah le dandelot....
Toujours une référence 30 ans après?

Tes posts me rappellent bien des souvenirs. Quand j'étais enfant, j'étais au conservatoire, j'y ai fait les 10 ans de solfège (ou plutôt formation musicale) obligatoire. Après moi j'ai jamais eu de difficulté avec les apprentissages "scolaires" donc ça m'allait.

C'est très intéressant pour moi (qui ai appris le solfège à une époque où on avait pas internet et les smartphones) de voir tous les outils pédagogiques existant maintenant.

Salut tout le monde,

Une question sur l'utilisation d'un titre de chanson suivi du mot "en" et d'un accord.
De plus en plus souvent, je me retrouve soit avec une grille d'accords, soit avec des paroles et des accords disséminés en fonction des changement d'accords.
Je crois avoir un peu près compris qu'en jouant ou répétant la fondamentale de l'accord pendant son temps de présence, je ne prends trop de risque de fusiller le passage quand je joue en groupe. Pour être tout à fait honnête et précis, je ne comprends pas bien ce que je fais, et je dis à peu près, parce que des fois je peux jouer une octave trop haut, et ça peut venir m'intriguer. Bon, en même temps, je suis à la basse donc personne ne remarque trop rien donc c'est plutôt pour moi.

Néanmoins, ça devient tout de suite moins drôle quand j'essaie de placer d'autres notes de l'accord (par exemple la 3 ou la 5 et/ou la 7 selon) au lieu de répéter la fondamentale. Et on finit de m'achever quand on me donne une feuille de paroles avec des accords, et qu'on me dit juste avant de partir : "Ah ouais en fait, on peut pas le jouer en Si mineur car la chanteuse ne peut pas y aller, donc on va le faire en La mineur. Bonnes révisions !".

Par exemple,

All along the watchtower de Bob Dylan, en La mineur

D'après ce que j'ai compris, on serait normalement en Si mineur sur ce morceau.
En l'état actuel de ce que je comprends, j'imagine donc une transposition d'un ton dans les graves de tout le morceau.
Comme la majorité des gens n'a pas l'oreille absolue (c'est mon cas) et n'attrape que les intervalles entre les notes, personne ne va trop relever cette entorse à l'absolu du morceau.
Et donc dans mon cas à la basse, il me suffit de me déplacer de 2 frettes vers le haut du manche à chaque fois que je vois une note.

- Est-ce que c'est bien ça ?
- Et si oui, pourquoi ne précise-t-on par la tonalité originale du morceau ?
- Comment sait-on qu'on est en Si mineur par défaut par exemple pour un morceau pour savoir de combien on doit transposer ? C'est le premier accord ? L'accord le plus fréquemment joué dans le morceau ?
- Est-ce que c'est parce que les musiciens ne finissent que par "penser" et jouer par intervalles, et plus par succession de notes ?

Je crois que j'avais déjà posé cette question quelque part et j'essaie de retrouver pour voir si ça me cause davantage aujourd'hui mais je ne retrouve plus !
Si quelqu'un a l'amabilité d'expliquer avec des exemples concrets svp

Comme je ne suis pas spécialiste en la matière, j'ai cherché sur internet et trouvé cette page qui répondra exactement à ta question

https://www.guitare-improvisation.com/analyser_trouver-une-tonalite.php

Merci Sarmat pour ton lien

Autre question du jour, une basse 4 cordes EADG a des cordes séparées par une quarte juste à chaque fois.
E -> A = 5 demi-tons (E,F,F#,G,G#,A)
A -> D = 5 demi-tons (A,A#,B,C,C#,D)
etc.

Je suis tombé sur une partition où c'est une basse 5 cordes normalement accordée, avec un tuning standard précisé donc BEADG. Pour moi, on a encore une quarte partout.
B -> E = 5 demi-tons (B,C,C#,D,D#,E)

Problème: la partition commence par ça


Pour moi, il n'y a problème que sur les basses 6 cordes (ou les guitares en EADGBE) avec un intervalle G -> B (G,G#,A,A#,B) qui a 4 demi-tons au lieu de 5. Et donc, la basse peut rester cette instrument de feignasse tant qu'on a pas cet intervalle G -> B qui oblige les guitaristes à connaître des positions changeantes selon les cordes.

Y-aurait-il une magie qui m'échappe encore ici ?
Pourquoi cette altération de la clé (si elle nécessaire sur la portée bien sûr) ?

Ah forcément si on entrave que dalle à l'armure, ça aide pas
Ça a été l'occasion de retomber sur la question que je posais juste avant bizarrement.

Je recommanderais bien cet article ainsi que les exemples dedans
https://tous-au-piano.com/comment-trouver-tonalite-morceau/

L'auteur a été un peu vite pour moi sur modes majeurs et les relatifs correspondant (pas évident si on a pas la liste).
Mais on les trouve ici : https://fr.wikipedia.org/wiki/Tonalit%C3%A9_relative

Code:

| *armure* | *mode majeur* | *mode mineur* |
| bbbbbbb  | Do♭           | La♭           |
| bbbbbb   | Sol♭          | Mi♭           |
| bbbbb    | Ré♭           | Si♭           |
| bbbb     | La♭           | Fa            |
| bbb      | Mi♭           | Do            |
| bb       | Si♭           | Sol           |
| b        | Fa            | Ré            |
|          | Do            | La            |
| #        | Sol           | Mi            |
| ##       | Ré            | Si            |
| ###      | La            | Fa♯           |
| ####     | Mi            | Do♯           |
| #####    | Si            | Sol♯          |
| ######   | Fa#           | Ré♯           |
| #######  | Do#           | La♯           |

Également, sur la 7ème du mode mineur. Il faut apparemment prendre la 7ème du mode mineur harmonique (et pas naturel).
Soit l'octave moins un demi-ton. Attention, pieds dans le plat pour la 7ème de Do# mineur, ça donne Si# (et non Do# - 1/2 ton = Do, même si Si# est confondu avec Do en tempérament égal).

Bon, je n'ai toujours pas compris si les altérations sur la clé ont des impacts sur les lignes concernées. Il me semble bien que oui, donc ma précédente question est toujours là mais ça ira bien pour maintenant déjà.

Une vidéo qui a réussi à me faire monter au cerveau la notion de key signature (surtout la raison du combo "clé"/"signature" en anglais)

https://youtu.be/_eKTOMhpy2w?t=326 a écrit:go up a "tone tone semitone tone tone tone semitone"
start anywhere and it will sound in a different place but you'll still be recognize a major scale

start for example on G
whole step whole step half step whole step whole step don't panic we can't go to that F because we need to go up a whole step so we have to go to f-sharp
and then finish off with a half step

so in order to play a scale of G major we have to use an F sharp and F sharp is what is known as the key signature of the scale of G major
in other words you can't play G major without an F sharp
that is what key signatures are they define what you need in order to be able to play that scale

take another one for example and start on D
whole step whole step to F sharp half step whole step whole step another whole step takes us to C sharp

so in order to play the scale of D major we have to use an F sharp in the C sharp
so we have to use two sharps to play the scale of D major and that means the key signature of D major, it's got two sharps in it F sharp and C sharp

EDIT : Je viens de m'appercevoir que le message oiriginal date de 2012... du coup ma réponse c'est un peu n'importe quoi

Moi a écrit:Salut salut

Vaste débat que le solfège en musique...

J'ai déjà rencontré un certain nombre de musiciens :
- Il y a celles et ceux qui ont fait le conservatoire, qui savent lire une partition à vue, qui sont de très bons techniciens mais s'avouent complétement perdus lorsqu'il est question d'improviser. C'est étrange, elles et ils connaissent leur instrument par coeur, sont de très bons musiciens lorsqu'il s'agit d'interprêter une pertition et pourtant ne savent pas comment improviser...
- Il y a celles et ceux qui ont appris sur le tas, ne connaissent pas le solfège, ne savent pas lire une partition mais peuvent être de très bons musiciens parce qu'ils jouent d'oreille.
- Et puis il y a celles et ceux qui savent faire les deux, et je pense que là ça doit être le pied !

Mais pour autant, si tu as une bonne oreille, le sens de la musique et la motivation, tu peux tout à fait apprendre à jouer d'un instrument sans pour autant connaitre le solfège. Je fais partie de la catégorie des gens qui ont une bonne oreille, le sens de la musique et qui se débrouillent assez bien pour s'en sortir grosso-modo sans savoir lire une partition. Surtout que parmi les instruments dont je joue, je ne vois même pas comment utiliser une partition vu qu'ils n'ont aucun "repères". Lame sonore (scie musicale), Theremin, se jouent d'oreille et essentiellement d'oreille. Je joue également de la clarinette, et c'est un instrument avec lequel j'arrive à improviser assez facilement.

Si je ne sais pas lire une partition, c'est juste à cause d'un handicap : Le fait d'être "doué" d'origine et d'avoir un gros poil dans la main ! Quand on a des facilités on a tendance à se reposer sur celles-ci. Au début on a pas besoin de trop bosser, on ne prend pas le goût au travail, et quand le niveau necessite de travailler, c'est mort ! Par contre, maintenant que je joue et que j'ai une motivation, de plus en plus je songe à me mettre à travailler, parce que j'ai envie d'aller plus loin.

Tout ça pour dire que selon moi, le plus important n'est pas de connaitre le solfège, le plus important est de pratiquer l'instrument de suite, de s'amuser, de se faire plaisir, de faire travailler son oreille, et puis soit ça suffira pour jouer et se faire plaisir, soit ça donnera suffisamment de motivation pour aborder l'apprentissage du solfège.

Dans ton cas, c'est plutôt l'aspect mathématique du solfège qui te bloque. Mais peut-être qu'il existe des méthodes d'apprentissages qui te conviendraient mieux. Parce que je n'ai pas l'impression qu'il faut avoir fait math sup / math spé pour comprendre. Je crois que c'est toi qui a évoqué la méthode Martenot. Je ne connais cette méthode que de nom, en revanche je connais les Ondes Martenot, instrument inventé par celui qui a inventé la méthode Martenot. Ce que je crois savoir, c'est qu'il était attaché aux ressentis, à la sensibilité musicale, à la pratique de l'instrument. Les Ondes Martenot reflétent cet état d'esprit. Je joue d'un instrument que j'ai fabriqué et qui est directement inspiré des Ondes Martenot (il reprend les grands principes et la même manière de commander le son) et c'est un instrument très expressif, qui fait appel à la sensibilité musicale.

Il est donc probable que la méthode Martenot te convienne plus qu'une méthode trop "scolaire".

En tout cas ce serait dommage que tu t'interdise d'apprendre à jouer d'un instrument au prétexte que tu ne connaisse pas le solfège. J'ai un truc pour apprendre à jouer, c'est très bête, mais tu te choisi des musiques que tu aime, des trucs pas trop difficiles, pas trop rapides, et tu essaye de jouer par dessus. Pas la mélodie, mais un accompagnement. Tu tente des notes, tu cherche les notes qui vont bien sur la musique, et puis après tu essaye d'improviser. Quand tu vas prendre de l'assurance tu pourras te lâcher et tu verras que parfois l'improvisation te permet d'être moins bloqué que si tu voulais faire attention à "bien faire".

Pour faire une analogie, je parlerais du roller. J'ai donné des cours de roller, et un exercice qui fait faire d'énormes progrès assez rapidement, c'est le jeu et notemment le hockey. Quand tu commence le roller, tu te bloque parce que tu veux "bien faire" et puis tu n'ose pas prendre de risques. Le hockey t'oblige à te concentrer sur la crosse et le palet. Résultat tu oublie que tu es sur des patins, tu ouoblie de "vouloir bien faire" et à des moments, tu te rends compte que tu as fait de gros progrès notamment sur les freinages. Là c'est pareil, tu te concentre sur la musique que tu veux accompagner, tu oublie de "vouloir bien faire" avec ton instrument, et ça te permet de débloquer des choses.

J'espère ne pas avoir raconter trop de bêtises, parce que après tout ça dépend peut-être aussi des personnalités de chacunes et chacuns.

Bon courage

(Hello, oui ce sont deux threads qui ont fusionné. C'est désormais plutôt la continuité du joyeux bazar que j'avais commencé dans un thread dédié et dans lequel on dépose principalement des questions, des liens et des vidéos autour de la théorie musicale)

Hello à tous,

après avoir fait du solfège étant gamine et n'en ayant pas un super souvenir, je n'arrivais à rien, je voulais seulement faire de la batterie pour me défouler

j'ai voulu reprendre le piano que j'ai pratiqué pendant quelques années sans aucun talent apparent, mais une certaine oreille musicale et un goût prononcé pour les mélodies, le chant...
Le problème, impossible de déchiffrer en jouant, je n'arrive même pas à comprendre comment ceux qui y parviennent font !?
en plus j'ai été diag Tdah donc ça n'aide pas à garder patience, comment font les pianistes par ici ?

Pour avoir quelques facilités en lecture à vue (sans pour autant être une exception), je peux donner un élément d'éclairage à Mianie0803 : ce qui facilite les choses, c'est d'avoir au moins quelques notions d'écriture et d'analyse. Le fait de comprendre ce qu'on joue aide beaucoup.