Accueil
Évènements
Rechercher
S'enregistrer
ConnexionEnigme: Questions 31 à 33
2 participants
Page 1 sur 1
Enigme: Questions 31 à 33
par DiyaR Mar 12 Nov 2013 - 0:07
Salut,
Ca vient d'un test de QI qui se fait en 2 semaines.
news.gen eriq.net/TL 37/tl 37.ht ml (enlevez les espaces)
Les questions 31 à 33 m'intriguent, notamment la 31:
Voici ce que je pense pour la 32 et la 33
Mais je ne comprends pas les exemples de la question 31.
Quelqu'un la comprends ?
Ca vient d'un test de QI qui se fait en 2 semaines.
news.gen eriq.net/TL 37/tl 37.ht ml (enlevez les espaces)
Les questions 31 à 33 m'intriguent, notamment la 31:
Voici ce que je pense pour la 32 et la 33
- Spoiler:
- Je pense que la 32 est un 4-cube et la 33 un 5-cube, car le nombre de chiffre semble affecter le nombre de dimensions.
Mais je ne comprends pas les exemples de la question 31.
Quelqu'un la comprends ?
Dernière édition par DiyaR le Sam 16 Nov 2013 - 14:59, édité 3 fois
DiyaR- Messages : 56
Date d'inscription : 09/11/2013
Re: Enigme: Questions 31 à 33
par JeanMath Jeu 14 Nov 2013 - 3:27
Pour rappel, une évaluation avec aide est une évaluation non fiable (juste comme ça, on sait jamais).
Je suis pas sûr à 100% hein, notamment au niveau des superpositions : quelles arêtes sont dissimulées par le n-cube gris (qu'on voit opaque dans l'exemple pour 122) ?
Cela dit la logique tient la route, j'vais l'expliquer si ça tente l'un de vous.
Je suis sûr que personne n'est encore convaincu. Bon, voici la démonstration :
- mes réponses:
Je suis pas sûr à 100% hein, notamment au niveau des superpositions : quelles arêtes sont dissimulées par le n-cube gris (qu'on voit opaque dans l'exemple pour 122) ?
Cela dit la logique tient la route, j'vais l'expliquer si ça tente l'un de vous.
Je suis sûr que personne n'est encore convaincu. Bon, voici la démonstration :
- la démo:
JeanMath- Messages : 661
Date d'inscription : 04/12/2012
Age : 32
Localisation : Clermont-Ferrand
Re: Enigme: Questions 31 à 33
par Invité Jeu 14 Nov 2013 - 11:32
mon idée était que 122 était la vue arrière du 22,
et je me suis trompé en effet, j'ai sans doute dessiné 121 au lieu de 111.
et je me suis trompé en effet, j'ai sans doute dessiné 121 au lieu de 111.
Invité- Invité
Re: Enigme: Questions 31 à 33
par DiyaR Ven 15 Nov 2013 - 1:25
Ok, merci à vous, je crois que j'ai pigé le truc.
Je sais pas si j'ai été clair, si non, je réexpliquerai.
- Spoil:
A la base j'étais parti sur un truc avec le point de vue.
Si je comprends bien semama t'avais dessiné un 112 (un 11 collé face du fond)
Donc quand on réalise un objet de dimension supérieure on transpose l'objet de dimension inférieure et on relie tous les angles (comme ils expliquent sur wikipedia). Si j'ai compris, on rajoute le chiffre correspondant au placement du n-cube gris dans à la nouvelle dimension, à la fin des chiffres qui existaient pour son placement dans la dimension d'en dessous (dans ton cas JeanMath), avec 2 la transposition la plus à droite.
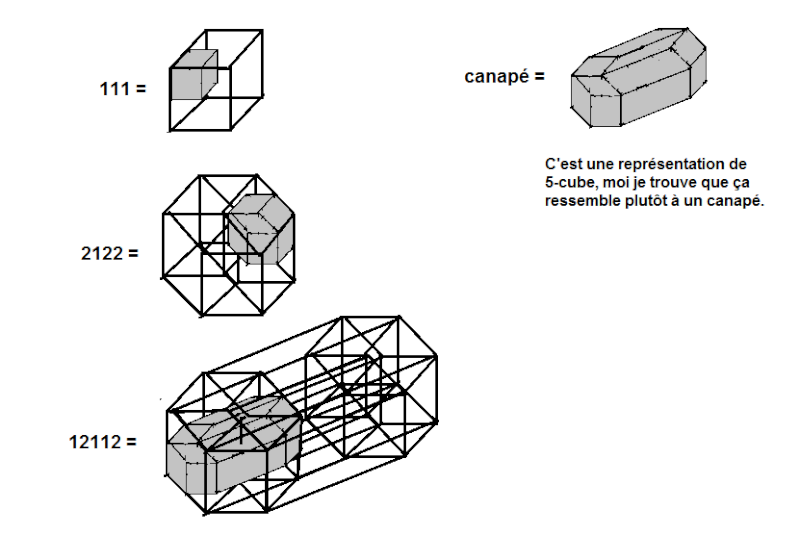
Pour 2122 je comprends: il est en contact avec l'image du cube de droite (dernier 2), sur sa face du fond (avant dernier 2), en haut (le 1) à droite (premier 2)
Par contre je comprends pas pour le canapé dans 12112.
Je l'aurais mis dans le 4-cube de droite vu que le dernier chiffre est un 2 ? (puis en contact avec le cube de gauche (dernier "1"), collé face avant (2eme "1"), puis en bas à gauche ("12").) Du coup il aurait été 2 fois plus court le canapé, ça fait un fauteuil ! (ou un canapé une place si vous préférez voir le verre à moitié plein
)
T'as raisonné avec les arêtes, tu peux m'expliquer ton raisonnement s'il te plait ? C'est par ce que j'ai pas eu le même qu'on est pas retombés sur les mêmes trucs
!!
Je sais pas si j'ai été clair, si non, je réexpliquerai.
DiyaR- Messages : 56
Date d'inscription : 09/11/2013
Re: Enigme: Questions 31 à 33
par JeanMath Ven 15 Nov 2013 - 2:09
Oh non, je crois que tu as eu le même raisonnement.
En fait les arêtes c'est autre chose : c'est plus de l'ordre de la fioriture, puisqu'au final ce qui est intéressant c'est de comprendre le code et de bien placer les n-cubes gris dans leurs homologues transparents. Les arêtes des n-cubes transparents sont soit devant les gris, soit derrière (et sont donc dissimulées), soit pire ! Elles peuvent les traverser.
Bon, à propos de cette histoire de 1 gauche et 2 droite, je m'étais déjà fait la réflexion suivante : au final, l'orientation de chaque "axe de dimension" est arbitraire. Alors on choisit selon ses goûts, et si on veut que le 2 désigne plutôt la gauche, pourquoi pas
Pour ma part, pour 12112, j'ai opté pour que le 5-cube démarre sur le 4-cube de gauche par soucis de lisibilité et de simplification du dessin.
Dans les exemples de départ, le premier chiffre (abscisses) donne 1 gauche vers 2 droite (intuitif) mais le second chiffre (ordonnées) donne 1 haut vers 2 bas (contre-intuitif), là ni gauche ni droite.
Pourquoi tu veux couper mon canapé ? Puisqu'au final, les arêtes des n-cubes gris sont deux fois plus courtes que leurs cousines sur le même "axe de dimension" dans les n-cubes transparents.
En fait les arêtes c'est autre chose : c'est plus de l'ordre de la fioriture, puisqu'au final ce qui est intéressant c'est de comprendre le code et de bien placer les n-cubes gris dans leurs homologues transparents. Les arêtes des n-cubes transparents sont soit devant les gris, soit derrière (et sont donc dissimulées), soit pire ! Elles peuvent les traverser.
Bon, à propos de cette histoire de 1 gauche et 2 droite, je m'étais déjà fait la réflexion suivante : au final, l'orientation de chaque "axe de dimension" est arbitraire. Alors on choisit selon ses goûts, et si on veut que le 2 désigne plutôt la gauche, pourquoi pas
Pour ma part, pour 12112, j'ai opté pour que le 5-cube démarre sur le 4-cube de gauche par soucis de lisibilité et de simplification du dessin.
Dans les exemples de départ, le premier chiffre (abscisses) donne 1 gauche vers 2 droite (intuitif) mais le second chiffre (ordonnées) donne 1 haut vers 2 bas (contre-intuitif), là ni gauche ni droite.
Pourquoi tu veux couper mon canapé ? Puisqu'au final, les arêtes des n-cubes gris sont deux fois plus courtes que leurs cousines sur le même "axe de dimension" dans les n-cubes transparents.
JeanMath- Messages : 661
Date d'inscription : 04/12/2012
Age : 32
Localisation : Clermont-Ferrand
Re: Enigme: Questions 31 à 33
par Invité Ven 15 Nov 2013 - 10:13
Complétement parti dans les décors pour moi, j'étais resté sur des mouvements de figures logiques, rien à voir avec les hypercubes.
Merci pour l'indication du wiki.
Merci pour l'indication du wiki.
Invité- Invité
Re: Enigme: Questions 31 à 33
par DiyaR Ven 15 Nov 2013 - 13:17
Ah oui exact, en tout cas merci de m'avoir expliqué, j'étais pas près de trouver. Je vais passer à une autre question maintenant la 37 par exempleJeanMath a écrit:
Pourquoi tu veux couper mon canapé ? Puisqu'au final, les arêtes des n-cubes gris sont deux fois plus courtes que leurs cousines sur le même "axe de dimension" dans les n-cubes transparents.
, qui à l'air ... assez facile !
DiyaR- Messages : 56
Date d'inscription : 09/11/2013
Re: Enigme: Questions 31 à 33
par JeanMath Ven 15 Nov 2013 - 13:44
Je sais pas si tu comptes envoyer tes réponses à l'auteur, mais si on admet que c'est une évaluation du QI alors ton résultat n'aura aucun sens. Ca se fait tout seul ces trucs.
Après, si ce ne sont que les côtés recherche de challenge et curiosité pour les solutions qui t'animent, y a pas de soucis.
Je ne donne plus de réponse en tout cas.
Après, si ce ne sont que les côtés recherche de challenge et curiosité pour les solutions qui t'animent, y a pas de soucis.
Je ne donne plus de réponse en tout cas.
JeanMath- Messages : 661
Date d'inscription : 04/12/2012
Age : 32
Localisation : Clermont-Ferrand
Re: Enigme: Questions 31 à 33
par DiyaR Ven 15 Nov 2013 - 17:00
Non je ne compte pas envoyer les réponses, c'est pour m'occuper (comme des mots-croisés). De temps en temps j'y jette un oeil et je me focalise sur une question. Ca dois faire 4 mois que je suis dessus de toute façon (au lieu des 2 semaines imparties) et c'est pas la première fois que je cherche des solutions en groupe.
Si vous comptez l'envoyer, n'ouvrez pas les spoiler. Vous aurez les réponses après l’envoi.
Toute façon on n'a pas respecté les volontés de l'auteur (moi encore moins!) "Do not discuss test items with others, either before, during or after taking the test and regardless if you intend to submit answers".
Si vous comptez l'envoyer, n'ouvrez pas les spoiler. Vous aurez les réponses après l’envoi.
Toute façon on n'a pas respecté les volontés de l'auteur (moi encore moins!) "Do not discuss test items with others, either before, during or after taking the test and regardless if you intend to submit answers".
DiyaR- Messages : 56
Date d'inscription : 09/11/2013
Sujets similaires» Énigme du 21
» Enigme (Facile)
» [Enigme] Le roi des nains
» Enigme démystification.
» ENIGME A RESOUDRE !!!
» Enigme (Facile)
» [Enigme] Le roi des nains
» Enigme démystification.
» ENIGME A RESOUDRE !!!
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum