Dieu tricote des chaussettes -- et je peux le prouver!
+17
Confiteor
Stegos
fift
Louna
Badak
Thaïti Bob
arôme naturel
Ardel
Azoth
david50
Harpo
ErikFromFrance
Pieyre
Cleore
Kass
♡Maïa
Petitagore
21 participants
Page 3 sur 4
Page 3 sur 4 •  1, 2, 3, 4
1, 2, 3, 4 
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Mog a écrit:Avec ce système qui permet de continuer ad vitam, tu n'as pas envie d'essayer d'y mettre des graines infinies pour voir ce qui se passe ?
Tu as bien choisi tes mots: je peux maintenant continuer ad vitam et non pas ad vitam aeternam: je peux envisager de lancer des calculs dont j'aurai le résultat dans un mois, cinq ans, vingt ans... Mais au-delà je risque fort d'avoir quitté cette vallée de larmes avant que le résultat (la génération où le serpicon commence à se stabiliser) ait été obtenu.
Je sais, parce que ça se démontre facilement, que la stabilisation de n'importe quel serpicon sur un cycle est inéluctable. Mais ce qui n'est pas du tout inéluctable, c'est que ça ait lieu dans un temps raisonnable (ne dépassant pas quelques dizaines d'années).
Ce que j'ai découvert au fond de mon impasse sombre, c'est qu'entre 144 et 145 cellules, un seuil de complexité est franchi. Alors que de 130 cellules à 131, de 131 à 132, de 132 à 133 etc., le nombre de générations nécessaire pour aboutir à une stabilisation est multiplié par une valeur à peine supérieure à 1 (de l'ordre de 1.2, au doigt mouillé)... Eh bien de 144 à 145 ça se multiplie au moins par vingt, d'un coup. Et j'en suis sur le cul.
A 143-144 cellules, on constate la stabilisation du serpicon au bout de quelques dizaines de millions de générations -- ce qui est quand même honorable. A 145 cellules, je n'ai pas encore une foule d'exemples à fournir tellement les calculs sont longs, mais sur onze essais je n'ai encore trouvé qu'un exemple d'une stabilisation se produisant avant cinq milliards de générations. J'ai l'impression d'assister là au déplacement d'une plaque tellurique: les continents bougent très lentement, n'avancent que de quelques millimètres par an, et puis vlan, d'un seul coup, il y a un séisme de magnitude 8 ou 9, et tout est déplacé de cinq à dix mètres d'un seul coup... eh bien il semble qu'on constate de telles disproportions dans l'étude des serpicons: d'un seul coup, la longévité du processus est multipliée par au moins 20... je n'ai pas encore assez de données pour donner une estimation plus sérieuse que ce "au moins", et je ne sais pas combien de mois de calculs il me faudra pour y parvenir. Je suis même tellement sur le cul que je ne parierais pas qu'il me sera possible de fournir un chiffre avant plusieurs années, ni même de mon vivant; la seule chose que mon intuition me dit, c'est "n'avance aucun chiffre, tu vas encore dire une connerie".
Si je n'ai aucune explication et aucun pronostic, je m'autorise quand même une remarque: cette valeur de 145 si particulière, je l'avais déjà remarquée dans ma collection de tunnels de générations paires: les très longs tunnels (plusieurs milliers de générations) sont relativement faciles à trouver avec des serpicons de 145 cellules, et je soupçonne que les deux phénomènes sont liés: abondance de longs tunnels = rareté des cycles finaux et difficulté à les atteindre. C'est relativement logique: les tunnels comme les cycles finaux emploient des générations canoniques (voir les épisodes précédents), toutes celles qui sont employées dans des tunnels sont par là-même impropres à être présentes dans un cycle final, et inversement.
Mais fondamentalement, je crains de ne pouvoir faire mieux pour le moment que de confesser mon absolue perplexité. Je m'oriente vers l'idée qu'il faut maintenant que je me mette à étudier les enchaînements de générations canoniques pour eux-mêmes, au lieu de me contenter de constater leur importance particulière au milieu du chaos de générations aléatoires.
Ah, encore une remarque importante. Le seul cycle final que jusqu'ici j'aie atteint avec 145 cellules a une longueur de 349 524 générations (ce qui se décompose en 73 * 19 * 7 * 3 * 3 * 2 * 2, mais cette remarque n'a peut-être aucun intérêt). Sa génération la plus facile à décrire (identifiée par l'algorithme décrit lors des épisodes précédents) comporte une seule cellule vivante (et 144 cellules mortes). Ça aussi, c'est peut-être un indice.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Chers lecteurs de ce fil, j'ai le plaisir, l'honneur et l'avantage de vous présenter ci-dessous le résumé de plusieurs mois de calculs, en même temps que, je crois, la preuve formelle qu'il y a bel et bien quelque chose d'important à découvrir dans l'étude de Serpicon. Bon, d'accord, on ne peut pas dire que l'image en question soit particulièrement sexy (ça ressemble furieusement à la copie d'écran d'un tableur, et en effet c'en est une), mais c'est la preuve formelle que la longueur des cycles de stabilisation de Serpicon entretient des rapports complexes avec la taille (en nombre de cellules) des anneaux où l'on constate ces stabilisations.
Dans la première colonne, vous avez le nombre de cellules dans un anneau Serpicon, par incrément de 60 à 144. En deçà de 60, je présume (peut-être à tort) qu'on ne constate rien de bien intéressant et que la plupart des serpicons aboutissent à des cycles très courts (et des dessins de chaussettes hyper-réguliers), parfois même à des cycles-néants d'une seule génération intégralement composée de cellules mortes, ce qui n'est pas très rigolo. Au-delà de 144, le nombre de générations précédant la stabilisation se compte en dizaines de milliards, et je n'ai pratiquement (pour le moment) aucune connaissance des cycles-chaussettes auxquels on aboutit.
Dans la deuxième colonne, vous trouvez la périodicité la plus fréquente pour les cycles de stabilisation avec le nombre de cellules correspondant. "La périodicité la plus fréquente", ça veut dire que c'est celle qu'on rencontre dans plus d'un cas sur deux, mais il peut y en avoir d'autres. Quand la deuxième périodicité la plus fréquente est assez fréquente pour être remarquée, je l'ai notée dans la troisième colonne.
Bon, ben, à partir de là, c'est à vous de montrer que vous êtes des zèbres et que vous remarquez des choses étranges dans ce tableau. Des choses étranges, il y en a vraiment plein plein plein, à commencer par le fait, qui me sidère, que ce tableau est vraiment tout sauf anarchique. J'attire aussi votre attention sur la fréquence à laquelle apparaissent (surtout dans la troisième colonne) des valeurs multiples d'une puissance de 2 minorée de 1.
Je n'ai pas la queue d'une explication à tous ces mystères. Mais je suis convaincu qu'il serait sensé de la chercher.

Bon, ben voilà une bonne chose de faite. Vos commentaires seront hyper-bienvenus.
Dans la première colonne, vous avez le nombre de cellules dans un anneau Serpicon, par incrément de 60 à 144. En deçà de 60, je présume (peut-être à tort) qu'on ne constate rien de bien intéressant et que la plupart des serpicons aboutissent à des cycles très courts (et des dessins de chaussettes hyper-réguliers), parfois même à des cycles-néants d'une seule génération intégralement composée de cellules mortes, ce qui n'est pas très rigolo. Au-delà de 144, le nombre de générations précédant la stabilisation se compte en dizaines de milliards, et je n'ai pratiquement (pour le moment) aucune connaissance des cycles-chaussettes auxquels on aboutit.
Dans la deuxième colonne, vous trouvez la périodicité la plus fréquente pour les cycles de stabilisation avec le nombre de cellules correspondant. "La périodicité la plus fréquente", ça veut dire que c'est celle qu'on rencontre dans plus d'un cas sur deux, mais il peut y en avoir d'autres. Quand la deuxième périodicité la plus fréquente est assez fréquente pour être remarquée, je l'ai notée dans la troisième colonne.
Bon, ben, à partir de là, c'est à vous de montrer que vous êtes des zèbres et que vous remarquez des choses étranges dans ce tableau. Des choses étranges, il y en a vraiment plein plein plein, à commencer par le fait, qui me sidère, que ce tableau est vraiment tout sauf anarchique. J'attire aussi votre attention sur la fréquence à laquelle apparaissent (surtout dans la troisième colonne) des valeurs multiples d'une puissance de 2 minorée de 1.
Je n'ai pas la queue d'une explication à tous ces mystères. Mais je suis convaincu qu'il serait sensé de la chercher.
Bon, ben voilà une bonne chose de faite. Vos commentaires seront hyper-bienvenus.
Dernière édition par Petitagore le Mar 23 Juin 2015 - 18:49, édité 1 fois (Raison : orthographe, cornegidouille!)
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
je t'invites très très chaudement, même brûlament ^^, à parcourir les pages du livre "Le Beau Livre des Maths" de Clifford Pickover éditions Dunod. Tu y prendras beaucoup de plaisir et ça te donnera plein d'idées et plein d'eau à ton moulin. Pas besoin de connaissances mathématiques, bien qu'en avoir permet bien sûr de mieux apprécier toutes les beautés qui y sont montrées. une page de texte, une illustration.
ton travail que je salue me fait penser à d'autres mystérieux motifs qu'on observe dans certains calculs ou représentations, que je mets en lien ci dessous. Pour moi, c'est de "l'ornithologie mathématique", je vins d'inventer cette expression, je la pratique aussi : observer les jolies choses qui se produisent dans la Nature (mathématique cette fois ci). On peut en tirer des théorèmes isolés, faire des conjectures, tout comme on étudie les comportements des oiseaux. Mais ça veut pas dire qu'on en extraira des vérités absolues qu'on va pouvoir sortir de leur contexte précis. Tout comme une fois qu'on a établi les motifs des plumes d'une certaine espèce, on a le résultat, mais il se suffit à lui même.
https://fr.wikipedia.org/wiki/Conjecture_de_Goldbach
https://www.google.fr/search?q=constante+de+feigenbaum&num=20&client=ubuntu&hs=nWm&channel=fs&source=lnms&tbm=isch&sa=X&ei=YZr0U528Acag0QWdmICADg&ved=0CAgQ_AUoAQ&biw=1329&bih=641
https://www.google.fr/search?q=constante+de+feigenbaum&num=20&client=ubuntu&hs=nWm&channel=fs&source=lnms&tbm=isch&sa=X&ei=YZr0U528Acag0QWdmICADg&ved=0CAgQ_AUoAQ&biw=1329&bih=641
ton travail que je salue me fait penser à d'autres mystérieux motifs qu'on observe dans certains calculs ou représentations, que je mets en lien ci dessous. Pour moi, c'est de "l'ornithologie mathématique", je vins d'inventer cette expression, je la pratique aussi : observer les jolies choses qui se produisent dans la Nature (mathématique cette fois ci). On peut en tirer des théorèmes isolés, faire des conjectures, tout comme on étudie les comportements des oiseaux. Mais ça veut pas dire qu'on en extraira des vérités absolues qu'on va pouvoir sortir de leur contexte précis. Tout comme une fois qu'on a établi les motifs des plumes d'une certaine espèce, on a le résultat, mais il se suffit à lui même.
https://fr.wikipedia.org/wiki/Conjecture_de_Goldbach
https://www.google.fr/search?q=constante+de+feigenbaum&num=20&client=ubuntu&hs=nWm&channel=fs&source=lnms&tbm=isch&sa=X&ei=YZr0U528Acag0QWdmICADg&ved=0CAgQ_AUoAQ&biw=1329&bih=641
https://www.google.fr/search?q=constante+de+feigenbaum&num=20&client=ubuntu&hs=nWm&channel=fs&source=lnms&tbm=isch&sa=X&ei=YZr0U528Acag0QWdmICADg&ved=0CAgQ_AUoAQ&biw=1329&bih=641

Thaïti Bob- Messages : 1850
Date d'inscription : 27/01/2012
Age : 37
Localisation : Avignon
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Allez hop on fait remonter le sujet !
Maintenant que le scénario est là, à quand Serpicon en animation, film, pièce de théâtre, etc. ?
L'hiver approche et des chaussettes à chiffres seraient les bienvenues !
Maintenant que le scénario est là, à quand Serpicon en animation, film, pièce de théâtre, etc. ?
L'hiver approche et des chaussettes à chiffres seraient les bienvenues !

arôme naturel- Messages : 140
Date d'inscription : 14/02/2012
Age : 57
Localisation : en mouvement
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
arôme naturel a écrit:Allez hop on fait remonter le sujet !
Maintenant que le scénario est là, à quand Serpicon en animation, film, pièce de théâtre, etc. ?
L'hiver approche et des chaussettes à chiffres seraient les bienvenues !
Teaser: Je réfléchis à un nouveau mode de représentation des cycles finaux et des tunnels. Prochainement sur vos écrans: les chaussettes du Bon Dieu comme vous ne les avez jamais vues.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Alors, alors ?? 
Bon, entre le café, la clope du matin, des questions se posent à moi...
J'ai bien compris que tu ne restes pas scotché devant ton écran pour observer les contorsions de ton Serpicon vu que l'ordinateur calcule bien plus vite qu'il n'affiche, mais alors concrètement, comment procèdes-tu pour observer et noter les périodicités remarquables ?
Tu génères une image a posteriori ?
Sinon... Pourquoi après 135 on retrouve 133 et 134 M'sieur ?
Bon, entre le café, la clope du matin, des questions se posent à moi...
J'ai bien compris que tu ne restes pas scotché devant ton écran pour observer les contorsions de ton Serpicon vu que l'ordinateur calcule bien plus vite qu'il n'affiche, mais alors concrètement, comment procèdes-tu pour observer et noter les périodicités remarquables ?
Tu génères une image a posteriori ?
Sinon... Pourquoi après 135 on retrouve 133 et 134 M'sieur ?
- Neurones:
- Et puis je me suis amusée à reprendre tes chiffres pour générer un graphique (juste pour voir). Les différences d'échelles rendent la lecture difficile mais le résultat comporte des analogies avec la propagation d'un potentiel d'action le long d'un axone neuronal (qui est un tube comme Serpicon).
Ça n'a sans doute rien à voir avec ton travail (d'ailleurs je le mets en spoiler pour pas déranger), mais je partage quelques propriétés remarquables qui m'ont fait penser à tes chaussettes :
- les canaux ioniques de la membrane du tube axonal peuvent être considérés comme ouverts ou fermés (excité/non excité ou 0/1 ou cellule vivante/cellule morte)
- la quantité de canaux ouverts ou fermés peut être comptée : au delà d'un seuil de canaux ouverts, il se produit spontanément un pic brutal (apparition du potentiel d'action)
- le potentiel d'action (pic) se propage ensuite de manière stable tout le long du tube par ouverture et fermeture des canaux
- le potentiel d’action obéit à la loi du tout ou rien et, une fois qu'il est apparu, il se propage sans atténuation d'amplitude, il s'autorégénère (Chaque PA généré localement possède ainsi une amplitude identique au PA qui l'a généré)
- la vitesse de propagation du potentiel d'action dépend principalement du diamètre de l'axone (plus le diamètre est grand, plus le courant circule vite)...
- ...mais aussi de la qualité intrinsèque des canaux (c'est à dire leur propre seuil de réaction vu que ce sont aussi des tubes) et de leur nombre autour du tube : ainsi certains axones vont réagir par une décharge rapide en début de stimulation puis ralentir leur décharge même si la stimulation reste forte et d'autres vont répondre à une stimulation constante par des décharges rythmées et répétées
C'est là que la mécanique quantique peut (soyons fous !) expliquer les comportements "bizarres" du Serpicon. Que se passe-t-il si l'on cesse de considérer que chaque cellule n'a que deux états ? L'ordinateur est très rapide pour faire passer la cellule d'un état à un autre, mais si on prend une (très grosse) loupe, il se passe peut-être exactement la même chose que lorsque tu retournes manuellement chaque petit triangle de ton Triancey lorsqu'une zone complète passe du rose au jaune ? Une cellule serait elle-même un tube avec un certain nombre d'états intermédiaires entre 0 et 1 ? (http://fr.wikipedia.org/wiki/Informatique_quantique)
Ah mince, du coup ça pose la question de l'influence de ton observation
Je m'égare

♡Maïa- Messages : 1734
Date d'inscription : 06/03/2012
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
58. l'Acte (2) : tout création est un commencement sans fin
[...]

MC Escher - Metamorphose
________________________________
Professore Piccolinopythagore ? Vous êtes toujours là ?
[...]
Pourtant, après la moisson inouïe de mes rêves depuis l'an dernier, et surtout des rêves métaphysiques et des rêves prophétiques, et aussi par la réflexion poursuivie avec l'écriture de La Clef des Songes, mon optique pour évaluer la place et la portée des choses s'est bien transformée. Je suis de moins en moins porté à me laisser impressionner par l'évidence écrasante du quantitatif, celle de la masse et du chiffre, cette pesante arme de choc de l'inertie. Je commence à me rendre compte que toute cette masse immense que Dieu, bien mieux que l'homme, sait jauger, ne pèse que d'un poids infime dans Ses balances ! Alors qu'un seul acte créateur, si infime qu'il puisse paraître, en tant qu'acte auquel Dieu Lui-même participe, a poids d'éternité. Je sais du moins, par un de mes rêves, qu'un tel acte vit à jamais dans la Mémoire de Dieu - gravé au même instant et avec un art achevé sur des plaques d'or fin, pour être conservé de toute éternité. Mais s'il est vrai que Dieu est Acte, sûrement la Mémoire de Dieu n'est archive ni tombeau-dépotoir de momies (fussent-elles en or et de toute beauté...), mais bien présence vivante en Dieu et, par là-même, appel à d'autres Actes en puissance. Des actes attendant leur heure, sous l'Œil vigilant de Dieu, pour naître et pour perpétuer et parfaire celui dont ils sont les fils.
Pour le dire autrement : tout acte créateur, si infime qu'il puisse paraitre et alors même qu'il semblerait à jamais perdu et oublié, est un commencement, géniteur fécond d'une suite sans fin d'actes issus de lui qui le continuent et le parachèvent. Toute création, en tant qu'œuvre qui n'est pas que de l'homme mais aussi de Dieu, a vie et valeur éternelle.
[...]La Clef des Songes - ou Dialogue avec le Bon Dieu
Alexandre Grothendieck 28 mars 1928 - 13 novembre 2014
Alexandre Grothendieck 28 mars 1928 - 13 novembre 2014

MC Escher - Metamorphose
________________________________
Professore Piccolinopythagore ? Vous êtes toujours là ?

arôme naturel- Messages : 140
Date d'inscription : 14/02/2012
Age : 57
Localisation : en mouvement
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
arôme naturel (citant Grothendieck) a écrit:Pour le dire autrement : tout acte créateur, si infime qu'il puisse paraitre et alors même qu'il semblerait à jamais perdu et oublié, est un commencement, géniteur fécond d'une suite sans fin d'actes issus de lui qui le continuent et le parachèvent. Toute création, en tant qu'œuvre qui n'est pas que de l'homme mais aussi de Dieu, a vie et valeur éternelle.
Peste! Je savais que Grothendieck était un grand bonhomme, mais je ne savais pas qu'il avait poussé vers la spiritualité et même vers la mystique... Merci de cette citation. Il m'arrive d'avoir des pensées voisines, si parva licet componere magnis, s'il est permis de comparer les petits aux grands -- mais c'est dit bien plus joliment que je n'aurais su non seulement le faire, mais même l'espérer.
Alexandre Grothendieck 28 mars 1928 - 13 novembre 2014
Ouais... A défaut d'être démontré, l'au-delà est clairement souhaitable pour des esprits pareils... et aussi, si on l'en croit, même pour des idées aussi insignifiantes que les chaussettes du Bon Dieu!
Merci pour Escher, je ne connaissais pas ces dessins-là, c'est splendide.
Professore Piccolinopythagore ? Vous êtes toujours là ?
Mais oui, et même je fais toujours tourner ma machine pour étudier les chaussettes du Bon Dieu... J'en suis actuellement aux anneaux de 163 cellules. Si au lieu d'avoir un ordinateur qui étudie des serpicons de plus en plus grands j'avais une sonde spatiale qui s'éloignait du soleil, je pense qu'elle serait quelque part entre les orbites de Saturne et de Neptune. Pousserai-je jusqu'à Uranus et Pluton, voire au-delà de la ceinture de Kuiper? Pas sûr, car les calculs deviennent tellement longs que je commence à me demander sérieusement si la loi de Moore suffira à me permettre d'aboutir à des résultats avant d'aller voir dans l'au-delà si Dieu existe...
J'ai assez envie de tenter une étude systématique des générations canoniques, dans l'espoir de comprendre pourquoi les périodicités de leurs cycles ne sont pas anarchiques et apparemment si souvent multiples de puissances de 2 minorées de 1 comme 63, 511, 1023, 2047, 4095. Evidemment, tous les nombres entiers sont au moins multiples de 2 puissance 1 moins 1 (de même que la valeur moyenne des angles d'un triangle est souvent proche de 60 degrés
Je vous tiendrai au courant!
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
comme quoi on ne sait pas tout  joli. moi qui n'aime pas les maths ...
joli. moi qui n'aime pas les maths ...
Invité- Invité
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Si vous avez aimé ce fil sur les chaussettes du Bon Dieu, Amazon pense que vous aimerez peut-être aussi cet autre ouvrage du même auteur. Le rapport ne vous paraîtra peut-être pas évident, mais il y en a bel et bien un, et comme c'est mon cerveau malade qui a accouché des deux, je pense que vous pouvez me croire sur parole.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Tout ça me fait penser aux crop circles. Aucun rapport sans doute, mais l'harmonie poétique et symétrique....

Louna- Messages : 80
Date d'inscription : 24/04/2015
Age : 62
Localisation : Perpignan
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Record battu dans ma collection de tunnels: désormais le plus long tunnel de générations paires "naturel" (obtenu à partir d'un mot-graine aléatoire) que l'humanité connaisse a une longueur de 6238 générations (avec 137 cellules). Le record précédent était de 5962 générations, avec 145 cellules.
Essayez de faire mieux, bande de nazes.
Essayez de faire mieux, bande de nazes.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Bonjour Petitagore, et merci pour ce post : je ne connaissais pas du tout, j'ai dévoré la première page et j'adore  .
.
Je m'y replonge ...
Je m'y replonge ...
fift- Messages : 8846
Date d'inscription : 26/04/2016
Age : 48
Localisation : Paris
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
J'essaie de reprendre les choses depuis le début...
Ce que je comprends, c'est ça :
Ce n'est pas grand-chose par rapport à ce que j'ai eu l'air de comprendre à la relecture de mes interventions. Désolé si j'ai aussi peu de mémoire...
Mais là, à partir de huit nombre entre 0 et 7, si on en obtient huit aussi, mais entre 0 et 1, on perd en information. Or, quand on passe d'une génération à l'autre, il s'agirait de la conserver.
C'est-à-dire que j'ai dû louper quelque chose. Est-ce que tu pourrais indiquer une loi d'évolution de la forme un+1 = f (un), où les termes de la suite (un) seraient homogènes ? Dans ce cas je te promets d'y réfléchir en matheux.
Ce que je comprends, c'est ça :
- Code:
Generation n 000 001 010 011 100 101 110 111
Generation n+1 0 1 1 0 1 0 0 0
Ce n'est pas grand-chose par rapport à ce que j'ai eu l'air de comprendre à la relecture de mes interventions. Désolé si j'ai aussi peu de mémoire...
Mais là, à partir de huit nombre entre 0 et 7, si on en obtient huit aussi, mais entre 0 et 1, on perd en information. Or, quand on passe d'une génération à l'autre, il s'agirait de la conserver.
C'est-à-dire que j'ai dû louper quelque chose. Est-ce que tu pourrais indiquer une loi d'évolution de la forme un+1 = f (un), où les termes de la suite (un) seraient homogènes ? Dans ce cas je te promets d'y réfléchir en matheux.
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Pieyre a écrit:Mais là, à partir de huit nombre entre 0 et 7, si on en obtient huit aussi, mais entre 0 et 1, on perd en information. Or, quand on passe d'une génération à l'autre, il s'agirait de la conserver.
C'est-à-dire que j'ai dû louper quelque chose. Est-ce que tu pourrais indiquer une loi d'évolution de la forme un+1 = f (un), où les termes de la suite (un) seraient homogènes ? Dans ce cas je te promets d'y réfléchir en matheux.
Désolé, je n'ai pas compris la question.
On ne part pas de huit nombres, on part d'un nombre quelconque (prédéterminé, mais qui peut être ce qu'on veut, de quelques unités à plusieurs dizaines, voire au-delà) de cellules (binaires), lequel nombre de cellules on découpe en paquets de trois qui se chevauchent. Si l'anneau de départ était "anneau", on le découperait en "ann", "nne", "nea", "eau", "aua" et "uan" -- avec un décalage d'un cran à chaque fois. Ensuite chacun de ces paquets de trois, rassemblant trois bits à la génération n, engendre un bit unique à la génération n+1.
Si tu parviens à dire ça d'une façon mathématiquement plus rigoureuse, je t'en serai reconnaissant.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
D'accord, j'ai compris, et je me souviens maintenant. En plus la réponse à ma question se trouvait dans le paragraphe qui précédait le morceau de code que j'ai cité... Il faut dire que je suis flemmard comme souvent les matheux et que je n'avais recherché dans tes interventions que des figures et d'éventuelles formules. Alors, j'avais bien compris qu'il n'y avait pas que huit éléments dans une génération mais c'est le recours au chevauchement qui me manquait.
Bon, j'essaie de poser le problème de façon mathématique, en reprenant les termes que tu emploies et en mentionnant les notions mathématiques associées.
Une chaussette est caractérisée par sa graine, qui correspond à la première génération de la chaussette, et par une loi de succession des générations. Si l'on fait abstraction du temps, c'est une suite (Gn).
Une génération est une structure finie de données, chacune de ces données pouvant prendre deux valeurs, qu'on peut fixer à 0 et 1 si l'on ne soucie pas de la représentation graphique. L'ensemble de base d'une génération est un n-uplet – c'est-à-dire une liste pour un informaticien –, qui est assortie d'une fonction successeur sur les indices S qui lui donne une forme cyclique.
Plus précisément, si une génération G a la forme (v0, v1..., vp-1), on a S (0) = 1, S (1) = 2..., S (p-1) = 0. C'est-à-dire qu'une génération correspond à une structure ℤ/pℤ réduite à la fonction successeur v -> v+1, structure dont on pourra donc utiliser les propriétés pour démontrer des résultats.
La succession entre deux générations peut être modélisée par une fonction F qui à la génération Gn = (vn,k)0⩽k⩽p-1 associe la génération Gn+1 = (vn+1,k)0⩽k⩽p-1 de la façon suivante :
F (vn+1,k) = f (vn,S-1(k), vn,k, vn,S(k)),
où la fonction f peut-être définie de façons diverses, ce qui constitue sans doute la principale difficulté du problème.
Première définition, par extension :
— f (0, 0, 0) = 0
— f (0, 0, 1) = 1
— f (0, 1, 0) = 1
— f (0, 1, 1) = 0
— f (1, 0, 0) = 1
— f (1, 0, 1) = 0
— f (1, 1, 0) = 0
— f (1, 1, 1) = 0
Deuxième définition, par une condition :
— Si l'une et une seule des valeurs u, v et w est égale à 1, alors f (u, v, w) = 1, sinon f (u, v, w) = 0.
Troisième définition, par une formule (pas excellente, mais je n'ai pas trouvé mieux) :
— f (u, v, w) = ((u + v + w) mod 3) mod 2, où la somme est calculée en considérant les valeurs u, v et w comme des entiers naturels.
En effet, la façon de définir est cruciale dans la perspective de démontrer des propriétés. Les deux premières définitions correspondent à un traitement par cas, ce qui est souvent ennuyeux, même si certains cas sont parfois triviaux. La troisième pourrait se prêter à à un calcul synthétique si elle n'était pas aussi complexe. D'ailleurs il faut remarquer que, si la loi de succession des générations avait été choisie de telle sorte que f (1, 1, 1) = 1, cette dernière forme aurait pu faciliter les démonstrations, dans la mesure où l'on aurait pu définir f par : f (u, v, w) = u + v + w (avec la somme de ℤ/2ℤ).
Voilà pour la formalisation, sauf erreur de ma part, ce qui m'arrive souvent – distraction oblige –, ou complication inutile – ce qui serait somme doute plus dommageable.
La prochaine étape à laquelle je vais m'appliquer, c'est de formaliser les résultats que tu as conjecturés, et puis de tâcher de les démontrer. Mais à chaque jour suffit sa peine.
Bon, j'essaie de poser le problème de façon mathématique, en reprenant les termes que tu emploies et en mentionnant les notions mathématiques associées.
Une chaussette est caractérisée par sa graine, qui correspond à la première génération de la chaussette, et par une loi de succession des générations. Si l'on fait abstraction du temps, c'est une suite (Gn).
Une génération est une structure finie de données, chacune de ces données pouvant prendre deux valeurs, qu'on peut fixer à 0 et 1 si l'on ne soucie pas de la représentation graphique. L'ensemble de base d'une génération est un n-uplet – c'est-à-dire une liste pour un informaticien –, qui est assortie d'une fonction successeur sur les indices S qui lui donne une forme cyclique.
Plus précisément, si une génération G a la forme (v0, v1..., vp-1), on a S (0) = 1, S (1) = 2..., S (p-1) = 0. C'est-à-dire qu'une génération correspond à une structure ℤ/pℤ réduite à la fonction successeur v -> v+1, structure dont on pourra donc utiliser les propriétés pour démontrer des résultats.
La succession entre deux générations peut être modélisée par une fonction F qui à la génération Gn = (vn,k)0⩽k⩽p-1 associe la génération Gn+1 = (vn+1,k)0⩽k⩽p-1 de la façon suivante :
F (vn+1,k) = f (vn,S-1(k), vn,k, vn,S(k)),
où la fonction f peut-être définie de façons diverses, ce qui constitue sans doute la principale difficulté du problème.
Première définition, par extension :
— f (0, 0, 0) = 0
— f (0, 0, 1) = 1
— f (0, 1, 0) = 1
— f (0, 1, 1) = 0
— f (1, 0, 0) = 1
— f (1, 0, 1) = 0
— f (1, 1, 0) = 0
— f (1, 1, 1) = 0
Deuxième définition, par une condition :
— Si l'une et une seule des valeurs u, v et w est égale à 1, alors f (u, v, w) = 1, sinon f (u, v, w) = 0.
Troisième définition, par une formule (pas excellente, mais je n'ai pas trouvé mieux) :
— f (u, v, w) = ((u + v + w) mod 3) mod 2, où la somme est calculée en considérant les valeurs u, v et w comme des entiers naturels.
En effet, la façon de définir est cruciale dans la perspective de démontrer des propriétés. Les deux premières définitions correspondent à un traitement par cas, ce qui est souvent ennuyeux, même si certains cas sont parfois triviaux. La troisième pourrait se prêter à à un calcul synthétique si elle n'était pas aussi complexe. D'ailleurs il faut remarquer que, si la loi de succession des générations avait été choisie de telle sorte que f (1, 1, 1) = 1, cette dernière forme aurait pu faciliter les démonstrations, dans la mesure où l'on aurait pu définir f par : f (u, v, w) = u + v + w (avec la somme de ℤ/2ℤ).
Voilà pour la formalisation, sauf erreur de ma part, ce qui m'arrive souvent – distraction oblige –, ou complication inutile – ce qui serait somme doute plus dommageable.
La prochaine étape à laquelle je vais m'appliquer, c'est de formaliser les résultats que tu as conjecturés, et puis de tâcher de les démontrer. Mais à chaque jour suffit sa peine.
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Pieyre a écrit:
Troisième définition, par une formule (pas excellente, mais je n'ai pas trouvé mieux) :
— f (u, v, w) = ((u + v + w) mod 3) mod 2, où la somme est calculée en considérant les valeurs u, v et w comme des entiers naturels.
Ca ne fonctionne pas pour f(0,0,0), si ?
fift- Messages : 8846
Date d'inscription : 26/04/2016
Age : 48
Localisation : Paris
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Je verrais plutôt quelque chose du genre :
f(u,v,w) = u(1-v)(1-w) + v(1-u)(1-w) + w(1-u)(1-v)
f(u,v,w) = u(1-v)(1-w) + v(1-u)(1-w) + w(1-u)(1-v)
fift- Messages : 8846
Date d'inscription : 26/04/2016
Age : 48
Localisation : Paris
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Pour f (0, 0, 0), ma formule fonctionne : (0 + 0 + 0) mod 3 = 0 et 0 mod 2 = 0. Je ne vois pas où tu as vu un problème.
Mais ta formulation est intéressante. Déjà elle est symétrique en les trois variables, ce qui fait qu'il suffit de vérifier les cas (0, 0, 0), (0, 0, 1), (0, 1, 1) et (1, 1, 1) pour la valider.
Et oui, ça marche ! Et la formule a l'avantage de ne faire intervenir que des calculs algébriques, et en plus sans qu'il soit question d'entiers naturels, ce qui pourrait être intéressant en vue de démonstration. Tu pourrais me dire comment tu as fait pour la trouver ?
Mais ta formulation est intéressante. Déjà elle est symétrique en les trois variables, ce qui fait qu'il suffit de vérifier les cas (0, 0, 0), (0, 0, 1), (0, 1, 1) et (1, 1, 1) pour la valider.
Et oui, ça marche ! Et la formule a l'avantage de ne faire intervenir que des calculs algébriques, et en plus sans qu'il soit question d'entiers naturels, ce qui pourrait être intéressant en vue de démonstration. Tu pourrais me dire comment tu as fait pour la trouver ?
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Pieyre a écrit:Pour f (0, 0, 0), ma formule fonctionne : (0 + 0 + 0) mod 3 = 0 et 0 mod 2 = 0. Je ne vois pas où tu as vu un problème.
Moi non plus …
Quant à t'expliquer comment j'ai trouvé ma formule, euh … je ne sais pas trop en fait.
Intuitivement, pour avoir quelques fois 0, et quelquefois 1, la multiplication de plusieurs facteurs me paraissait le plus pertinent : il suffit qu'un des facteurs soit égal à zéro pour que tout le terme le soit aussi. Du coup, avec trois facteurs couvrant les trois inconnues, et en soustrayant 1 à deux des inconnues, on couvre le cas où si la première inconnue est égale à 1, le résultat est positif, et si une seule des deux autres inconnues est égale à 1, le résultat est 0.
Il suffit alors d'additionner trois termes en faisant tourner les inconnues par permutation circulaire pour arriver à la formule finale.
fift- Messages : 8846
Date d'inscription : 26/04/2016
Age : 48
Localisation : Paris
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Merci, c'est intuitif mais suffisamment logique quand on a l'habitude des raisonnements formels.
Avec tout ça, même si, dans la perspective de démontrer des propriétés de façon minimale, il me semble intéressant de trouver une formule algébrique compacte, il n'empêche que cela ne convient pas à tous les problèmes. Ainsi, il n'y aurait pas de telle formule dans le cas de la résolution du cube de Rubik : il y a des méthodes plus efficaces mais, quant à la solution optimale, ce serait celle qui correspond au minimum de coups parmi toutes les configurations (ou une certaine classe de configurations), voilà tout. C'est-à-dire qu'on ne peut espérer une solution algébrique minimale qu'en fonction de la structure du problème et du langage qui permet de l'exprimer.
Ainsi, concernant la fonction de succession entre deux générations, il sera peut-être préférable de se tenir, pour les démonstrations des propriétés globales, à un traitement par cas calqué sur l'un un algorithme de calcul. J'indique pour mémoire les deux formes envisageables, sans chercher à les optimiser (par exemple en réutilisant une somme partielle utilisée pour la cellule précédente afin de calculer la cellule courante) puisque ce n'est pas le but ici.
Avec tout ça, même si, dans la perspective de démontrer des propriétés de façon minimale, il me semble intéressant de trouver une formule algébrique compacte, il n'empêche que cela ne convient pas à tous les problèmes. Ainsi, il n'y aurait pas de telle formule dans le cas de la résolution du cube de Rubik : il y a des méthodes plus efficaces mais, quant à la solution optimale, ce serait celle qui correspond au minimum de coups parmi toutes les configurations (ou une certaine classe de configurations), voilà tout. C'est-à-dire qu'on ne peut espérer une solution algébrique minimale qu'en fonction de la structure du problème et du langage qui permet de l'exprimer.
Ainsi, concernant la fonction de succession entre deux générations, il sera peut-être préférable de se tenir, pour les démonstrations des propriétés globales, à un traitement par cas calqué sur l'un un algorithme de calcul. J'indique pour mémoire les deux formes envisageables, sans chercher à les optimiser (par exemple en réutilisant une somme partielle utilisée pour la cellule précédente afin de calculer la cellule courante) puisque ce n'est pas le but ici.
- Forme 1, en 4 cas :
- si u = 0
si v = 0
f <- w
sinon
f <- non w
sinon
si v = 1
f <- 0
sinon
f <- non w
- Forme 2, en 2 cas :
- si u + v + w = 1
f = 1
sinon
f = 0
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
1 - Code is law
2 - Golly, sur Android et Apple
Avec Golly, on doit pouvoir reproduire le Serpicon, ou contacter l'auteur du programme pour qu'il ajoute cette fonctionnalité.
La montée en puissance du calcul informatique est telle que, entre l'ouverture de ce post, et maintenant, un "bête" téléphone est probablement capable de faire plus qu'un ordinateur au début du post.
Et les lanceurs, les vers, les banques....ça me rappelle de vieux, mais alors VIEUX souvenirs
2 - Golly, sur Android et Apple
Avec Golly, on doit pouvoir reproduire le Serpicon, ou contacter l'auteur du programme pour qu'il ajoute cette fonctionnalité.
La montée en puissance du calcul informatique est telle que, entre l'ouverture de ce post, et maintenant, un "bête" téléphone est probablement capable de faire plus qu'un ordinateur au début du post.
Et les lanceurs, les vers, les banques....ça me rappelle de vieux, mais alors VIEUX souvenirs

Stegos- Messages : 4567
Date d'inscription : 18/02/2018
Age : 105
Localisation : 3ème planète autour du soleil
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Stegos a écrit:1 - Code is law
2 - Golly, sur Android et Apple
Pour Golly, je suppose que tu parles de ça; merci du tuyau, j'espère trouver le temps de creuser... mais ce ne sera pas tout de suite. En revanche, je ne vois pas de quoi tu parles avec "Code is law", je suis preneur d'un lien.
La montée en puissance du calcul informatique est telle que, entre l'ouverture de ce post, et maintenant, un "bête" téléphone est probablement capable de faire plus qu'un ordinateur au début du post.
C'est vrai, mais c'est encore plus vrai avec un ordinateur d'aujourd'hui. D'ailleurs, chaque fois que mon ordi rend l'âme (le précédent a duré sept ans), je refais tourner mes listings sur mon nouvel ordi neuf et constate aussitôt que la frontière a reculé. Mais pas tant que cela, cela dit: plus il y a de cellules dans le Serpicon, plus les tunnels sont rares, plus les stabilisations sur un cycle ont lieu tard, et cette croissance est encore plus exponentielle que la loi de Moore.
Dernière édition par Petitagore le Mar 27 Fév 2018 - 20:38, édité 1 fois (Raison : pétouille stylistique)
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
BingoPetitagore a écrit:
Pour Golly, je suppose que tu parles de ça; merci du tuyau, j'espère trouver le temps de creuser... mais ce ne sera pas tout de suite.
Ok, je vais essayer d'être bref (j'ai dit essayer, pas réussir)Petitagore a écrit:
En revanche, je ne vois pas de quoi tu parles avec "Code is law", je suis preneur d'un lien.
Au départ, c'est une remarque presque philisophique...
Code is law...c'est ce qui nous attend tous dans un avenir proche
Ça fait écho à la pensée de Lawrence Lessig : https://framablog.org/2010/05/22/code-is-law-lessig/
Quand tu dis Dieu tricote des chaussettes -- et je peux le prouver!, en fait, c'est pas Dieu.
Tu vas dire......ce sont les math...
Sauf que ce ne sont pas les math...c'est toi....
Sauf que c'est pas toi..c'est ton code...
Et c'est même pire, c'est l'implémentation de ton code qui est la loi....Code is law.
Si ton code est top nickel, sans bugs, alors...c'est peut être toi...et peut être les maths...
J'ai longtemps joué avec des ordinateurs, du code, et des "jeux stupides", comme celui du jeu de la vie, ou du "renard / lapin"...avec des ordinateurs que j’assemblais avec des fers à souder, et où la mémoire se comptait en kilo octets (oui oui, kilo)
Et j'ai vu des "trucs" superbes qui en fait n'étaient que des vilains bugs dans mon code...mais parfois les effets de bord sont inattendus...
Code is Law
C'est aussi ce qui nous pend au nez...enfin, ce qu'on va se prendre dans la gueule en fait...
exemple...
Tu veux freiner avec ta voiture, là, tout de suite, pour ne pas emplafonner le gamin qui traverse sans regarder...
Toi, tu appuies sur la pédale...mais c'est pas toi qui freine vraiment...
la voiture à probablement un ABS (obligatoire en europe depuis 2009
Ce n'est plus toi qui limite le freinage...
Ce ne sont plus les lois de la physique qui limitent le freinage.
C'est l'implémentation du code dans le boîtier.....Code is law...
Et quand on sait que, dans certaines circonstances, l'ABS rallonge significativement les distances de freinage...code is law.
Un autre exemple bien flippant ?
Tu veux un crédit pour quelque chose (maison, études ,voiture)....on te dis poliment non...pourquoi...c'est l'ordinateur qui dit non....Code is law.
Ce qu'on te dira pas c'est....
Ton iphone dis que tu marche pas assez par jour (ok, ou ton iwatch, ou ton bracelet connecté)
Ta carte de credit dit que tu vas trop souvent au fast food
Ta voiture dit que tu roules trop vite
Ton smartphone dis que tu sors pas assez de chez toi
Facebook dit que tu penses mal, ou que tu es déprimé
Tes recherches google montrent que tu penses mal, ou que tu es dépressif, etc etc..
On ne te le dira jamais....on dira...l'ordinateur à dit que.....Code is law
Petitagore a écrit:
C'est vrai, mais c'est encore plus vrai avec un ordinateur d'aujourd'hui. D'ailleurs, chaque fois que mon ordi rend l'âme (le précédent a duré sept ans), je refais tourner mes listings sur mon nouvel ordi neuf et constate aussitôt que la frontière a reculé. Mais pas tant que cela, cela dit: plus il y a de cellules dans le Serpicon, plus les tunnels sont rares, plus les stabilisations sur un cycle ont lieu tard, et cette croissance est encore plus exponentielle que la loi de Moore.
Avant de jeter ton ordi....si ce n'est pas déjà fait, y mettre un VRAI système d'exploitation, optimisé, ça peut être bien....
L'avantage du smartphone c'est qu'on peut "jouer" avec toute la journée, le portable aussi, mais c'est moins pratique.
Et avec des quad / octo / deca cores....la puissance est plus que respectable.

Bref....j'ai dit bref non....aïe...pataper..pataper....

Stegos- Messages : 4567
Date d'inscription : 18/02/2018
Age : 105
Localisation : 3ème planète autour du soleil
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Ben c'était passionnant, notamment l'infographie. Merci.
Mes machines tournent sous Linux depuis, euh... entre 1999 et 2002. si Linux n'est pas un vrai système d'exploitation, ben il va falloir que tu m'en suggères un autre -- et probablement sur un autre fil, pour qu'on puisse troller.
Je joue avec ma tablette toute la journée (quand je ne suis pas devant mon ordi de bureau). Je ne sais pas s'il est légitime de dire, ou de contester, qu'elle a un "vrai" système d'exploitation... mais c'est une tablette Android (de marque Lenovo: tout bas de gamme). Quand je joue avec, ma façon de faire la plus courante est de me connecter en SSH à l'un ou l'autre de mes deux serveurs Linux -- lesquels, je crois, disposent d'un vrai système d'exploitation.
Stegos a écrit:Avant de jeter ton ordi....si ce n'est pas déjà fait, y mettre un VRAI système d'exploitation, optimisé, ça peut être bien...
Mes machines tournent sous Linux depuis, euh... entre 1999 et 2002. si Linux n'est pas un vrai système d'exploitation, ben il va falloir que tu m'en suggères un autre -- et probablement sur un autre fil, pour qu'on puisse troller.
L'avantage du smartphone c'est qu'on peut "jouer" avec toute la journée, le portable aussi, mais c'est moins pratique.
Je joue avec ma tablette toute la journée (quand je ne suis pas devant mon ordi de bureau). Je ne sais pas s'il est légitime de dire, ou de contester, qu'elle a un "vrai" système d'exploitation... mais c'est une tablette Android (de marque Lenovo: tout bas de gamme). Quand je joue avec, ma façon de faire la plus courante est de me connecter en SSH à l'un ou l'autre de mes deux serveurs Linux -- lesquels, je crois, disposent d'un vrai système d'exploitation.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Petitagore a écrit:
Mes machines tournent sous Linux depuis, euh... entre 1999 et 2002. si Linux n'est pas un vrai système d'exploitation, ben il va falloir que tu m'en suggères un autre -- et probablement sur un autre fil, pour qu'on puisse troller.
Ahhhh, tu es donc un mec bien....

Here : Windoze free since the last millenium
Et pour les autres....vouaip, Linux c'est devenu un vrai kilckÔdrôme, comme Windaube....vous devriez essayer...

Petitagore a écrit:
Quand je joue avec, ma façon de faire la plus courante est de me connecter en SSH à l'un ou l'autre de mes deux serveurs Linux -- lesquels, je crois, disposent d'un vrai système d'exploitation.
Ahhhhhh
 Yes
Yes En plus, si je dis du mal de Linux, Linus va me faire la gueule et ça va prendre des plombes pour lui expliquer que non...c'est juste un joke...

Bon, dis, on cause un rien de whatsapp / threema / telegram / signal....passke il y a dans le coin des
 ki z'ont pas tout compris à la vie privée...
ki z'ont pas tout compris à la vie privée... 

Stegos- Messages : 4567
Date d'inscription : 18/02/2018
Age : 105
Localisation : 3ème planète autour du soleil
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Le copier-coller, c'est pas fait pour les chiens...
Record battu dans ma collection de tunnels: désormais le plus long tunnel de générations paires "naturel" (obtenu à partir d'un mot-graine aléatoire) que l'humanité connaisse a une longueur de 6592 générations (avec 137 cellules). Le record précédent était de 6238 générations, également avec 137 cellules.
Essayez de faire mieux, bande de nazes.
Petitagore a écrit:Record battu dans ma collection de tunnels: désormais le plus long tunnel de générations paires "naturel" (obtenu à partir d'un mot-graine aléatoire) que l'humanité connaisse a une longueur de 6238 générations (avec 137 cellules). Le record précédent était de 5962 générations, avec 145 cellules.
Essayez de faire mieux, bande de nazes.
Record battu dans ma collection de tunnels: désormais le plus long tunnel de générations paires "naturel" (obtenu à partir d'un mot-graine aléatoire) que l'humanité connaisse a une longueur de 6592 générations (avec 137 cellules). Le record précédent était de 6238 générations, également avec 137 cellules.
Essayez de faire mieux, bande de nazes.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Eh bien, le nouveau record du monde n'aura pas tenu longtemps...
Trois jours plus tard seulement, le voici pulvérisé (ce qui témoigne du fait que parfois de petites astuces algorithmiques suffisent à changer les résultats du tout au tout). Dans ma collection de tunnels, désormais le plus long tunnel de générations paires "naturel" (obtenu à partir d'un mot-graine aléatoire) que l'humanité connaisse a une longueur de 8061 générations (avec 145 cellules). Le record précédent, très inférieur donc, était de "seulement" 6592 générations, avec 137 cellules.
Vous voyez qu'il était possible de faire mieux, bande de nazes.
Edit: En fait, j'ai trouvé quelques heures plus tôt un tunnel de 8018 générations (record qui n'aura donc tenu que quelques heures). Mais on ne va pas pinailler.
Petitagore a écrit:Record battu dans ma collection de tunnels: désormais le plus long tunnel de générations paires "naturel" (obtenu à partir d'un mot-graine aléatoire) que l'humanité connaisse a une longueur de 6592 générations (avec 137 cellules). Le record précédent était de 6238 générations, également avec 137 cellules.
Trois jours plus tard seulement, le voici pulvérisé (ce qui témoigne du fait que parfois de petites astuces algorithmiques suffisent à changer les résultats du tout au tout). Dans ma collection de tunnels, désormais le plus long tunnel de générations paires "naturel" (obtenu à partir d'un mot-graine aléatoire) que l'humanité connaisse a une longueur de 8061 générations (avec 145 cellules). Le record précédent, très inférieur donc, était de "seulement" 6592 générations, avec 137 cellules.
Vous voyez qu'il était possible de faire mieux, bande de nazes.
Edit: En fait, j'ai trouvé quelques heures plus tôt un tunnel de 8018 générations (record qui n'aura donc tenu que quelques heures). Mais on ne va pas pinailler.
Dernière édition par Petitagore le Mer 11 Mar 2020 - 20:19, édité 1 fois
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Continue !
Ça m'éclate de te voir faire. Dans les années 2000 j'ai beaucoup joué avec les automates programmables, les fractales, les "lanceurs" etc.
Ça m'éclate de te voir faire. Dans les années 2000 j'ai beaucoup joué avec les automates programmables, les fractales, les "lanceurs" etc.

Confiteor- Messages : 9150
Date d'inscription : 01/04/2017
Age : 65
Localisation : Drôme
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
De mon côté, il y a un truc qui me préoccupe, c'est la fonction de Fift :
f(u,v,w) = u(1-v)(1-w) + v(1-u)(1-w) + w(1-u)(1-v)
Oui, je sais, c'était il y a deux ans et demi; mais il n'y a pas d'heure pour les braves.
Je ne sais pas comment tu fais pour battre tes records; mais, à mon avis, en formalisant mieux le problème, il doit être possible de fournir une suite dont la limite du nombre de générations soit infinie (ce qui ne serait pas naze, reconnais-le).
Alors, ce qui m'embête dans cette fonction, bien que symétrique en les trois variables, c'est qu'elle n'est pas assez compacte, autrement pas assez générale. Or, souvent c'est en généralisant un problème que l'on finit par le résoudre (ainsi que d'autres problèmes par la même occasion). C'est la leçon que j'ai retenue du grand mathématicien Alexandre Grothendieck.
Si je note (u1, u2, u3) = u le vecteur que j'avais nommé (u, v, w) et ui* la valeur 1 - ui (par défaut de disposer de la notation surlignée qui est plus attestée pour cela) j'obtiens :
f (u) = somme des ui × uj* × uk* pour i, j et k successifs dans l'ordre cyclique des indices.
Tu vas me dire : c'est encore plus compliqué. Eh bien, pour un mathématicien, non.
À suivre...
f(u,v,w) = u(1-v)(1-w) + v(1-u)(1-w) + w(1-u)(1-v)
Oui, je sais, c'était il y a deux ans et demi; mais il n'y a pas d'heure pour les braves.
Je ne sais pas comment tu fais pour battre tes records; mais, à mon avis, en formalisant mieux le problème, il doit être possible de fournir une suite dont la limite du nombre de générations soit infinie (ce qui ne serait pas naze, reconnais-le).
Alors, ce qui m'embête dans cette fonction, bien que symétrique en les trois variables, c'est qu'elle n'est pas assez compacte, autrement pas assez générale. Or, souvent c'est en généralisant un problème que l'on finit par le résoudre (ainsi que d'autres problèmes par la même occasion). C'est la leçon que j'ai retenue du grand mathématicien Alexandre Grothendieck.
Si je note (u1, u2, u3) = u le vecteur que j'avais nommé (u, v, w) et ui* la valeur 1 - ui (par défaut de disposer de la notation surlignée qui est plus attestée pour cela) j'obtiens :
f (u) = somme des ui × uj* × uk* pour i, j et k successifs dans l'ordre cyclique des indices.
Tu vas me dire : c'est encore plus compliqué. Eh bien, pour un mathématicien, non.
À suivre...
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Eh bien! Moi qui croyais que j'étais le dernier et seul lecteur de ce fil... 
Je n'ai pas compris un mot à ce que tu dis, Pieyre, mais je t'encourage quand même à marcher sur les pas de Grothendieck. Pour ma part, eh bien vous avez pu le constater, je n'ai pas lâché le morceau, et j'ai des projets de recherche selon de nouvelles techniques algorithmiques, même si c'est encore assez fumeux dans ma tête. Mais je me suis déniaisé en langage Rust l'été dernier, et ça m'a donné envie de chercher dans cette direction.
Toujours à suivre, donc.
Je n'ai pas compris un mot à ce que tu dis, Pieyre, mais je t'encourage quand même à marcher sur les pas de Grothendieck. Pour ma part, eh bien vous avez pu le constater, je n'ai pas lâché le morceau, et j'ai des projets de recherche selon de nouvelles techniques algorithmiques, même si c'est encore assez fumeux dans ma tête. Mais je me suis déniaisé en langage Rust l'été dernier, et ça m'a donné envie de chercher dans cette direction.
Toujours à suivre, donc.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Pieyre, tu me vois honoré d'avoir fourni une formule qui te préoccupe, fut-ce 2 ans et demi après  .
.
J'ai toujours aimé les maths, mais de manière très intuitive et mon niveau est celui d'un première année de licence. Du coup, je regrette de ne pas avoir poursuivi*.
Sinon, je souscris à ta proposition de rédaction de ma formule, effectivement plus "formelle" et surtout plus facilement généralisable à un nombre d'indices quelconque (voire infini ?).
* mais la relève est prête : mini-fift 1 veut faire Normale Sup pour pouvoir être docteur en maths
 .
.J'ai toujours aimé les maths, mais de manière très intuitive et mon niveau est celui d'un première année de licence. Du coup, je regrette de ne pas avoir poursuivi*.
Sinon, je souscris à ta proposition de rédaction de ma formule, effectivement plus "formelle" et surtout plus facilement généralisable à un nombre d'indices quelconque (voire infini ?).
* mais la relève est prête : mini-fift 1 veut faire Normale Sup pour pouvoir être docteur en maths

fift- Messages : 8846
Date d'inscription : 26/04/2016
Age : 48
Localisation : Paris
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Bon, je passe en notation matricielle, ce qui permet de généraliser en dimension quelconque.
La fonction de Fift ressemble fort à un produit scalaire de vecteurs, sauf qu'il y aurait trois vecteurs. Mais, qu'à cela ne tienne... on peut toujours s'arranger.
Alors, je considère u = (ui)i:1..n un vecteur assimilable à une matrice colonne U, et u* le vecteur ayant pour composantes les ui*.
Si j'appelle I la matrice identité et D la matrice de décalage cyclique des composantes de u, j'obtiens la formule suivante (ou le point désigne le produit scalaire transposé aux matrices colonnes) :
f (u) = U.(DU*I)(D2U*)
Bon, en fait je fais le malin mais ce n'est pas satisfaisant du tout : la formule est plus générale mais à peine (il y a toujours trois termes dans le produit) et puis elle n'est pas symétrique en les trois termes du produit. Par ailleurs, cela ne fait pas avancer d'un iota dans la résolution du problème. Mais, si cela peut intéresser suffisamment les matheux pour qu'ils proposent mieux, ce sera toujours ça de gagné...
Fift : j'espère qu'on ne va pas attendre que ton fils ou ta fille ait obtenu son doctorat pour résoudre enfin cette question...
La fonction de Fift ressemble fort à un produit scalaire de vecteurs, sauf qu'il y aurait trois vecteurs. Mais, qu'à cela ne tienne... on peut toujours s'arranger.
Alors, je considère u = (ui)i:1..n un vecteur assimilable à une matrice colonne U, et u* le vecteur ayant pour composantes les ui*.
Si j'appelle I la matrice identité et D la matrice de décalage cyclique des composantes de u, j'obtiens la formule suivante (ou le point désigne le produit scalaire transposé aux matrices colonnes) :
f (u) = U.(DU*I)(D2U*)
Bon, en fait je fais le malin mais ce n'est pas satisfaisant du tout : la formule est plus générale mais à peine (il y a toujours trois termes dans le produit) et puis elle n'est pas symétrique en les trois termes du produit. Par ailleurs, cela ne fait pas avancer d'un iota dans la résolution du problème. Mais, si cela peut intéresser suffisamment les matheux pour qu'ils proposent mieux, ce sera toujours ça de gagné...
Fift : j'espère qu'on ne va pas attendre que ton fils ou ta fille ait obtenu son doctorat pour résoudre enfin cette question...
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
J'ajoute juste une petite chose encore. Mais je n'embêterai pas davantage Petitagore avec mes ratiocinations concernant la seule notation mathématique de propriétés abstraites. Je promets que je vais enfin me mettre à étudier sa méthode (d'ailleurs je l'ai déjà dit, donc cela ne me coûte rien de plus de le promettre à nouveau).
Si je considère un nombre quelconque de variables u1, u2..., un pour la fonction de Fift, il n'est pas si difficile d'obtenir une forme compacte :
f (u) = Σi=1..n ui Πj=1..n, j≠i uj*
C'est en gros la même chose que ce qu'a écrit Fift, sinon que je préfère noter l'expression 1 - x par x* pour rendre compte du fait que les nombres 0 et 1 considérés ici constituent une algèbre de Boole où il n'y a pas par construction de soustraction.
Et, sous forme matricielle :
f (u) = tU פi=1..n-1 DiU*
où je note tU la transposée de la matrice U, et où la lettre hébraïque פ (choisie parce que la lettre grecque Π était déjà prise) désigne un produit scalaire généralisé entre les matrices colonnes correspondant à un nombre quelconque de vecteurs.
Oui, on va me dire : ta notation est peut-être simple pour toi, mais déjà ton explication est compliquée... Bah, oui, mais ça c'est propre à la discipline mathématique, et même à toute montée en abstraction. Cela me rappelle une anecdote, sans doute inventée, qu'un ami qui a travaillé chez IBM il y a une trentaine d'années m'a racontée. Il s'agissait de compacter de gros fichiers à l'aide d'un programme de codage associé. Jusqu'à présent, on n'avait pu compacter une certaine base de données qu'en 16 disquettes. Un jour, un employé annonce qu'il a réussi à le faire en une disquette seulement; — forte impression; — oui, mais il me faut pour cela 15 disquettes pour stocker le programme de codage...
Si je considère un nombre quelconque de variables u1, u2..., un pour la fonction de Fift, il n'est pas si difficile d'obtenir une forme compacte :
f (u) = Σi=1..n ui Πj=1..n, j≠i uj*
C'est en gros la même chose que ce qu'a écrit Fift, sinon que je préfère noter l'expression 1 - x par x* pour rendre compte du fait que les nombres 0 et 1 considérés ici constituent une algèbre de Boole où il n'y a pas par construction de soustraction.
Et, sous forme matricielle :
f (u) = tU פi=1..n-1 DiU*
où je note tU la transposée de la matrice U, et où la lettre hébraïque פ (choisie parce que la lettre grecque Π était déjà prise) désigne un produit scalaire généralisé entre les matrices colonnes correspondant à un nombre quelconque de vecteurs.
Oui, on va me dire : ta notation est peut-être simple pour toi, mais déjà ton explication est compliquée... Bah, oui, mais ça c'est propre à la discipline mathématique, et même à toute montée en abstraction. Cela me rappelle une anecdote, sans doute inventée, qu'un ami qui a travaillé chez IBM il y a une trentaine d'années m'a racontée. Il s'agissait de compacter de gros fichiers à l'aide d'un programme de codage associé. Jusqu'à présent, on n'avait pu compacter une certaine base de données qu'en 16 disquettes. Un jour, un employé annonce qu'il a réussi à le faire en une disquette seulement; — forte impression; — oui, mais il me faut pour cela 15 disquettes pour stocker le programme de codage...
Dernière édition par Pieyre le Jeu 12 Mar 2020 - 18:03, édité 1 fois
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Juste pour la beauté formelle de la chose (autrement appelé coupage de cheveux en quatre)
devrait plutôt s'écrire :
f(u,v,w) = u(1-v)(1-w) + v(1-w)(1-u) + w(1-u)(1-v)
C'est quand même beaucoup plus joli !
Pieyre a écrit:
f(u,v,w) = u(1-v)(1-w) + v(1-u)(1-w) + w(1-u)(1-v)
devrait plutôt s'écrire :
f(u,v,w) = u(1-v)(1-w) + v(1-w)(1-u) + w(1-u)(1-v)
C'est quand même beaucoup plus joli !
fift- Messages : 8846
Date d'inscription : 26/04/2016
Age : 48
Localisation : Paris
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Oui, tu as raison (si l'on peut parler de raison pour ce qui concerne l'élégance); mais pas de problème : c'est bien comme ça que je l'avais pris.
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Pieyre a écrit:J'ajoute juste une petite chose encore. Mais je n'embêterai pas davantage Petitagore avec mes ratiocinations concernant la seule notation mathématique de propriétés abstraites.
Non, non, ça ne m'embête pas du tout, ça me réjouit, au contraire, que mon petit bazar algorithmique puisse être étudié par d'authentiques mathématiciens... Le seul problème, c'est que je ne comprendrai rien à leurs recherches, mais je ne veux surtout pas les décourager ni décourager les autres lecteurs... y compris les mathématiciens des générations futures!
En revanche, je vais peut-être réinsister sur un point: de toute évidence (enfin, quand on a étudié le bazar assez longtemps, comme je l'ai fait), parmi toutes les combinaisons de 0 et de 1 envisageables, il y en a une catégorie particulière qui ont une importance capitale. Ce sont celles que j'ai (improprement) appelées plus haut des "générations canoniques", c'est-à-dire les cas de figure où... bon, pour ne pas compliquer à loisir, je vais me limiter à l'hypothèse où le nombre total de cellules dans un anneau est pair. Eh bien, dans cette hypothèse, les combinaisons où tous les 1 sont isolés et, en prime, tous séparés les uns des autres par un nombre impair de zéros... eh bien ces combinaisons ont une importance capitale et méritent assurément une étude à part.
Exemple d'une telle combinaison ("combinaison" n'est sans doute pas le bon terme, "arrangement" serait déjà moins faux): 00000000000100010101000000010101010001 (en n'oubliant pas que cette suite boucle sur elle-même, et qu'on peut sans rien changer prendre des chiffres à gauche pour les replacer à droite; il s'agit d'un collier, pas d'un empilement).
A mon avis (d'informaticien), le premier pas à franchir pour étudier ces combinaisons d'importance primordiale, c'est d'essayer de compter leur nombre au sein de toutes les combinaisons-arrangements-colliers envisageables (elles, déjà comptées par György Pólya sous le nom poétique de "colliers de Pólya" (or Pólya necklaces if you want to google that in English). Jusqu'à 20-26 cellules, je pense pouvoir sans trop de peine trouver un moyen informatique d'en faire un inventaire ordonné... mais une belle formule truffée de factorielles serait certainement plus élégante.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Oui, j'ai commencé à regarder tout ça. Et même je suis en train de tout relire et de tout définir de façon à répondre à un certain nombre de questions que tu nous as posées. Maintenant, je ne suis pas forcément plus optimiste qu'un météorologue à qui l'on demanderait de prévoir le temps à cent jours. Mais, enfin, cela permettra peut-être de dégrossir certains problèmes.
Mais, pour la dernière fois, je vais en rajouter une couche concernant la fonction de Fift (enfin, qu'il m'en excuse : juste la formulation de Fift de la fonction de... je ne sais quoi – à définir), parce que je ne voudrais pas que quelqu'un débarque en me disant : mais il y avait plus simple, enfin, quel naze tu fais !
Alors, dans mon intervention du 13 juillet 2017, j'avais tout pour simplifier la formule et je ne l'ai pas fait.
En effet, j'avais remarqué que f (u, v, w), c'était u + v + w (modulo 2) sauf pour u = v = w = 1.
Aussi il aurait suffit de poser f (u, v, w) = u + v + w - uvw.
On peut d'ailleurs le montrer à partir de la formule de Fift :
f (u, v, w) = u(1 - v)(1 - w) + v(1 - w)(1 - u) + w(1 - u)(1 - v)
soit u + v + w - 2(uv + vw + wu) + 3uvw
soit u + v + w + uvw
Eh oui, quand on réduit les calculs dans ℤ/2ℤ (autrement dit l'algèbre de Boole correspondant à l'ensemble {0, 1}), tout nombre pair est équivalent à 0 et tout nombre impair à 1.
Maintenant, vous allez me dire que ce n'est pas exactement pareil... Mais si : dans ℤ/2ℤ, la soustraction et la multiplication, c'est la même chose.
Ces propriétés évidentes, je les découvre maintenant, parce qu'à 56 ans et des milliers d'heures de prises de tête sur des questions mathématiques complexes, je n'ai jamais fait sur les entiers de calcul formel (autrement dit avec des variables) en une autre base que la base 10. Cela m'étonne moi-même.
Bon, alors, ce n'est pas généralisable en un nombre quelconque de variables :
f (u1, u2) = u1 + u2
f (u1, u2, u3) = u1 + u2 + u3 + u1u2u3
f (u1, u2, u3, u4) = u1 + u2 + u3 + u4 + u1u2u3 + u2u3u4 + u3u4u1 + u4u1u2
Je ne vais pas plus loin, parce que cela me barbe de faire les calculs à la main, mais on peut tout de même conjecturer le résultat suivant : f (u) = somme des produits impairs de composantes.
Bon, en pratique, si Petitagore a choisi trois composantes, j'imagine que c'était pour une raison de symétrie, et qu'il aurait bien pu en prendre cinq ou tout nombre impair, aussi qu'on pourrait trouver une formule générale pour les cas de ce type.
Mais il n'est sans doute pas nécessaire de généraliser à l'excès. Je crois avoir suffisamment montré à quel degré d'abstraction cela nous conduisait.
Aussi, dans le cas de trois composantes, du point du vue du calcul comme de celui de la démonstration, on pourra considérer l'une des deux formes :
— si toutes les composantes sont 1, alors f (u) = 0, sinon f (u) = somme des composantes;
— f (u) = somme + produit des composantes.
Alors, il s'agit pour en finir de faire retour sur les pérégrinations formelles qui m'ont conduit à ce résultat simplifié. Selon moi elles n'étaient pas inutiles. Déjà j'ai pu réviser mes bases, notamment du côté du calcul matriciel (je ne savais plus bien faire le produit de deux matrices de dimensions différentes, c'est dire) et des nombres p-adiques. Ensuite, c'était une façon de comprendre à quel point il est utile de généraliser mais que parfois on se laisse entraîner à complexifier juste pour le plaisir.
Voilà : c'est tout pour cette petite question; désormais je me concentre sur l'essentiel.
Mais, pour la dernière fois, je vais en rajouter une couche concernant la fonction de Fift (enfin, qu'il m'en excuse : juste la formulation de Fift de la fonction de... je ne sais quoi – à définir), parce que je ne voudrais pas que quelqu'un débarque en me disant : mais il y avait plus simple, enfin, quel naze tu fais !
Alors, dans mon intervention du 13 juillet 2017, j'avais tout pour simplifier la formule et je ne l'ai pas fait.
En effet, j'avais remarqué que f (u, v, w), c'était u + v + w (modulo 2) sauf pour u = v = w = 1.
Aussi il aurait suffit de poser f (u, v, w) = u + v + w - uvw.
On peut d'ailleurs le montrer à partir de la formule de Fift :
f (u, v, w) = u(1 - v)(1 - w) + v(1 - w)(1 - u) + w(1 - u)(1 - v)
soit u + v + w - 2(uv + vw + wu) + 3uvw
soit u + v + w + uvw
Eh oui, quand on réduit les calculs dans ℤ/2ℤ (autrement dit l'algèbre de Boole correspondant à l'ensemble {0, 1}), tout nombre pair est équivalent à 0 et tout nombre impair à 1.
Maintenant, vous allez me dire que ce n'est pas exactement pareil... Mais si : dans ℤ/2ℤ, la soustraction et la multiplication, c'est la même chose.
Ces propriétés évidentes, je les découvre maintenant, parce qu'à 56 ans et des milliers d'heures de prises de tête sur des questions mathématiques complexes, je n'ai jamais fait sur les entiers de calcul formel (autrement dit avec des variables) en une autre base que la base 10. Cela m'étonne moi-même.
Bon, alors, ce n'est pas généralisable en un nombre quelconque de variables :
f (u1, u2) = u1 + u2
f (u1, u2, u3) = u1 + u2 + u3 + u1u2u3
f (u1, u2, u3, u4) = u1 + u2 + u3 + u4 + u1u2u3 + u2u3u4 + u3u4u1 + u4u1u2
Je ne vais pas plus loin, parce que cela me barbe de faire les calculs à la main, mais on peut tout de même conjecturer le résultat suivant : f (u) = somme des produits impairs de composantes.
Bon, en pratique, si Petitagore a choisi trois composantes, j'imagine que c'était pour une raison de symétrie, et qu'il aurait bien pu en prendre cinq ou tout nombre impair, aussi qu'on pourrait trouver une formule générale pour les cas de ce type.
Mais il n'est sans doute pas nécessaire de généraliser à l'excès. Je crois avoir suffisamment montré à quel degré d'abstraction cela nous conduisait.
Aussi, dans le cas de trois composantes, du point du vue du calcul comme de celui de la démonstration, on pourra considérer l'une des deux formes :
— si toutes les composantes sont 1, alors f (u) = 0, sinon f (u) = somme des composantes;
— f (u) = somme + produit des composantes.
Alors, il s'agit pour en finir de faire retour sur les pérégrinations formelles qui m'ont conduit à ce résultat simplifié. Selon moi elles n'étaient pas inutiles. Déjà j'ai pu réviser mes bases, notamment du côté du calcul matriciel (je ne savais plus bien faire le produit de deux matrices de dimensions différentes, c'est dire) et des nombres p-adiques. Ensuite, c'était une façon de comprendre à quel point il est utile de généraliser mais que parfois on se laisse entraîner à complexifier juste pour le plaisir.
Voilà : c'est tout pour cette petite question; désormais je me concentre sur l'essentiel.
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Merveilles de l'algorithmique et du web, j'ai retrouvé sur the On-line Encyclopedia of Integer Sequences (OEIS) le nombre de colliers de Polya qu'on peut faire avec un nombre de perles donné et des perles de deux couleurs.
Je m'attaque à trouver le nombre de colliers "canoniques".
Et si vous ne comprenez rien à ce que je raconte, c'est pas grave, je le note principalement ici pour ne plus paumer la référence. Mais ça a vraiment un rapport avec le sujet de ce fil.
Mais ça a vraiment un rapport avec le sujet de ce fil.
Je m'attaque à trouver le nombre de colliers "canoniques".
Et si vous ne comprenez rien à ce que je raconte, c'est pas grave, je le note principalement ici pour ne plus paumer la référence.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
En revanche, l'On-line Encyclopedia of Integer Sequences ne connaît pas la suite suivante:
2,2,2,3,3,5,5,8,9,14,16,26,31,49,64,99,133,209,291,455,657,1022,1510,2359
... ce qui m'incite à penser que décidément, vraiment pas grand-monde ne s'est encore intéressé à mon problème des générations canoniques. Il s'agit des nombres de colliers différents que l'on peut constituer, avec des perles de deux couleurs en nombre défini, en s'imposant pour contrainte que toutes les perles d'une couleur (une seule parmi les deux) soient isolées (ou plus exactement, qu'on ne trouve jamais deux perles qui se touchent dans l'une des deux couleurs -- une seule parmi les deux).
Ouais, je sais, faudrait dire ça de façon plus rigoureuse. Faites pas chier, accrochez-vous (même si s'accrocher à un collier, c'est un moyen très sûr pour faire rouler toutes les perles par terre façon Castafiore mais je m'égare).
Par exemple, voici la liste classée des 16 colliers respectant cette condition quand il y a 11 perles (mes colliers sont composés de 1 et de 0, et j'ai choisi de ne retenir que les colliers où les 1 sont isolés). Il y en a seize, pas un de plus, pas un de moins.
1 - 00000000000
(oui, je considère que quand il n'y a pas du tout de 1, ben il n'y a pas non plus un 1 à côté d'un autre 1)
2 - 00000000001
3 - 00000000101
4 - 00000001001
5 - 00000010001
6 - 00000010101
7 - 00000100001
8 - 00000100101
9 - 00001000101
10 - 00001001001
11 - 00001010101
12 - 00010001001
13 - 00010010101
14 - 00010100101
15 - 00100100101
16 - 00101010101
Essayez-vous à en trouver un dix-septième, vous verrez que ce sera forcément une variante d'un des 16 que j'ai listés et que vous n'aurez réussi qu'à énumérer le collier en partant d'une autre perle et/ou en le renversant.
Eh bien, figurez-vous qu'avec 24 perles représentées par des 1 et des 0 (je ne suis pas allé au-delà), alors qu'on obtient quand même 352.698 colliers différents (ce qui soit dit en passant est quand même déjà beaucoup, beaucoup moins que 2 puissance 24, qui vaut 16.777.216), eh bien on ne trouve plus que 2359 colliers avec des 1 tous isolés, pas un de moins, pas un de plus.
Tout ce que j'appelle des "générations canoniques" est composé de colliers avec des 1 isolés, mais ce n'est pas la seule condition: il y a donc encore moins de générations canoniques (je ne vais pas tarder à vous donner la quantité exacte jusqu'à 24 perles). Donc, en proportion, ça fait vraiment très très très peu... mais en nombre absolu, ça croît quand même exponentiellement à mesure que le nombre de perles augmente, et c'est ça qui est fun: une proportion infime d'un nombre gigantesque, ça peut déjà faire pas mal.
Je ne sais pas du tout si qui que ce soit peut me suivre dans mon délire, mais moi je me marre bien.
2,2,2,3,3,5,5,8,9,14,16,26,31,49,64,99,133,209,291,455,657,1022,1510,2359
... ce qui m'incite à penser que décidément, vraiment pas grand-monde ne s'est encore intéressé à mon problème des générations canoniques. Il s'agit des nombres de colliers différents que l'on peut constituer, avec des perles de deux couleurs en nombre défini, en s'imposant pour contrainte que toutes les perles d'une couleur (une seule parmi les deux) soient isolées (ou plus exactement, qu'on ne trouve jamais deux perles qui se touchent dans l'une des deux couleurs -- une seule parmi les deux).
Ouais, je sais, faudrait dire ça de façon plus rigoureuse. Faites pas chier, accrochez-vous (même si s'accrocher à un collier, c'est un moyen très sûr pour faire rouler toutes les perles par terre façon Castafiore mais je m'égare).
Par exemple, voici la liste classée des 16 colliers respectant cette condition quand il y a 11 perles (mes colliers sont composés de 1 et de 0, et j'ai choisi de ne retenir que les colliers où les 1 sont isolés). Il y en a seize, pas un de plus, pas un de moins.
1 - 00000000000
(oui, je considère que quand il n'y a pas du tout de 1, ben il n'y a pas non plus un 1 à côté d'un autre 1)
2 - 00000000001
3 - 00000000101
4 - 00000001001
5 - 00000010001
6 - 00000010101
7 - 00000100001
8 - 00000100101
9 - 00001000101
10 - 00001001001
11 - 00001010101
12 - 00010001001
13 - 00010010101
14 - 00010100101
15 - 00100100101
16 - 00101010101
Essayez-vous à en trouver un dix-septième, vous verrez que ce sera forcément une variante d'un des 16 que j'ai listés et que vous n'aurez réussi qu'à énumérer le collier en partant d'une autre perle et/ou en le renversant.
Eh bien, figurez-vous qu'avec 24 perles représentées par des 1 et des 0 (je ne suis pas allé au-delà), alors qu'on obtient quand même 352.698 colliers différents (ce qui soit dit en passant est quand même déjà beaucoup, beaucoup moins que 2 puissance 24, qui vaut 16.777.216), eh bien on ne trouve plus que 2359 colliers avec des 1 tous isolés, pas un de moins, pas un de plus.
Tout ce que j'appelle des "générations canoniques" est composé de colliers avec des 1 isolés, mais ce n'est pas la seule condition: il y a donc encore moins de générations canoniques (je ne vais pas tarder à vous donner la quantité exacte jusqu'à 24 perles). Donc, en proportion, ça fait vraiment très très très peu... mais en nombre absolu, ça croît quand même exponentiellement à mesure que le nombre de perles augmente, et c'est ça qui est fun: une proportion infime d'un nombre gigantesque, ça peut déjà faire pas mal.
Je ne sais pas du tout si qui que ce soit peut me suivre dans mon délire, mais moi je me marre bien.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
En consultant ce matin ta nouvelle contribution, je me suis dit : c'est fastoche ! Et j'étais prêt à répondre dans les dix minutes qu'il suffisait de prendre ta liste de 11 séquences par la fin, en choisissant 0 ou 1, ce qui faisait un facteur 2, puis que chaque 1 devait être suivi d'un 0 avant qu'on puisse choisir un 0 ou un 1, d'où un nouveau facteur 2, d'où finalement une puissance de 2, à diviser par le nombre de décalages pour se ramener à un collier.
Et puis, en émergeant de ma torpeur matinale, je me suis rendu compte que ce n'était pas si simple. Le problème n'est évidemment pas symétrique en les 0 que l'on peut répéter et les 1 que l'on ne peut pas. Mais, qu'à cela ne tienne : dans ce genre de cas, il suffit de tracer un arbre des configurations, en induire une formule et la démontrer.
Ce n'est que dans un troisième temps que j'ai compris que ce n'était toujours pas aussi simple...
Mais, pour ajouter tout de même quelque chose sur le plan mathématique (sinon je risque d'abandonner la chose, ce qui serait dommage), je vais tout de même exposer la méthode que j'ai commencé de suivre dans le deuxième temps, qui fournira au moins une borne du nombre de colliers (un mathématicien, c'est comme ça : tu lui demandes combien vaut f (n), il te répond que c'est entre g (n) et h (n) et il est content de lui; ou alors que c'est à peu près k (n) et il est content aussi).
Alors, voilà : on prend tes listes par la droite, on remonte vers la gauche, et cela donne :
— liste vide : 1 (je ne suis pas sûr que ce soit utile, mais c'est en vue de généraliser);
— listes de 1 perle : 2, soit : 0 et 1 – c'est aussi le nombre de colliers;
— listes de 2 perles : 3, soit 00, 01 et 10 – nombre de colliers : 2, soit 00 et 01;
— listes de 3 perles : 5, soit 000, 001, 010, 100 et 101 – nombre de colliers : 2, soit 000 et 001;
— etc.
Eh bien, en traçant l'arbre des possibilités pour les listes de perles, c'est clair : quand une perle est 0, elle donne deux branches : 0 et 1; alors que si elle est 1, il n'y a qu'une branche : 0.
À partir de cela, si l'on note un le nombre de branches qui donnent 0 à l'étape n et vn le nombre de branches qui donnent 1, on obtient :
un+1 = un + vn (tout nombre peut être suivi d'un 0)
vn+1 = un (seuls les 0 peuvent être suivis d'un 1)
Bon, les lecteurs attentifs se rendront compte que cette formulation ne tient pas compte du fait que l'on considère des colliers, c'est-à-dire des listes qui bouclent sur elles-mêmes. Mais je verrai ça plus tard (un mathématicien, c'est comme ça : tu lui poses un problème complexe, il répond à un problème plus simple, parce que ça pourra toujours servir, même s'il aurait été préférable de commencer autrement dès le début).
C'est-à-dire qu'on peut affirmer que le nombre de listes de 0 et de 1 qui répondent à la contrainte (hormis en leurs bornes) est un + vn (soit on termine par un 0, soit par un 1).
Alors, pour résoudre le système récurrent, qui est un cas de récurrence mutuelle, c'est simple puisque le système est linéaire (pas de produits ou autres complications). Et pour cela il y a des méthodes.
En l'occurrence :
un+2 = un+1 + vn+1 = un+1 + un
D'où l'équation récurrente d'ordre 2 :
un+2 - un+1 - un = 0
Qui a pour équation caractéristique :
X2 - X - 1 = 0
Dont les solutions sont :
X1 = (1 + √5)/2 et X2 = (1 - √5)/2
Et là on peut exprimer directement un en fonction de u1 à l'aide de la puissance d'une matrice.
Sauf qu'on va prendre un raccourci, parce qu'en chemin on a reconnu que les un correspondaient à la suite de Fibonacci F, plus précisément que un = Fn+1.
Or, si l'on note φ = (1 + √5)/2 et φ' = (1 - √5)/2, on a : Fn = 1/√5 (φn - φ'n).
Déjà cela permet de calculer un et donc un + vn qui, je le rappelle, est le nombre de listes de 0 et de 1 qui répondent à ta construction (hormis la condition de boucle caractéristique des colliers, malheureusement).
Maintenant, grâce à Wikipédia, je me rends compte que la valeur Fn, pour des questions de convergence, c'est l'entier le plus proche de 1/√5 φn.
Cela nous donne une valeur du nombre de listes considérées :
un + vn = un+1 = Fn+2 ≃ (1 + √5)n+2/(2n+2√5)
Alors, tant que je ne me suis pas coltiné le problème du collier en tant que tel (le fait qu'il soit cyclique), cette valeur ne représente qu'une majoration du nombre à trouver.
Mais voici pour comparer :
Valeurs que tu indiques :
2, 2, 2, 3, 3, 5, 5, 8, 9, 14, 16, 26, 31, 49, 64, 99, 133, 209, 291, 455, 657, 1022, 1510, 2359
Valeurs majorantes que je trouve (qui correspondent à la suite de Fibonacci) :
2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584
Bon, ce n'est pas tout à fait ça, mais avoue que cela ressemble, dans la façon de progresser... Avec encore un peu de travail, ça devrait le faire.
Et puis, en émergeant de ma torpeur matinale, je me suis rendu compte que ce n'était pas si simple. Le problème n'est évidemment pas symétrique en les 0 que l'on peut répéter et les 1 que l'on ne peut pas. Mais, qu'à cela ne tienne : dans ce genre de cas, il suffit de tracer un arbre des configurations, en induire une formule et la démontrer.
Ce n'est que dans un troisième temps que j'ai compris que ce n'était toujours pas aussi simple...
Mais, pour ajouter tout de même quelque chose sur le plan mathématique (sinon je risque d'abandonner la chose, ce qui serait dommage), je vais tout de même exposer la méthode que j'ai commencé de suivre dans le deuxième temps, qui fournira au moins une borne du nombre de colliers (un mathématicien, c'est comme ça : tu lui demandes combien vaut f (n), il te répond que c'est entre g (n) et h (n) et il est content de lui; ou alors que c'est à peu près k (n) et il est content aussi).
Alors, voilà : on prend tes listes par la droite, on remonte vers la gauche, et cela donne :
— liste vide : 1 (je ne suis pas sûr que ce soit utile, mais c'est en vue de généraliser);
— listes de 1 perle : 2, soit : 0 et 1 – c'est aussi le nombre de colliers;
— listes de 2 perles : 3, soit 00, 01 et 10 – nombre de colliers : 2, soit 00 et 01;
— listes de 3 perles : 5, soit 000, 001, 010, 100 et 101 – nombre de colliers : 2, soit 000 et 001;
— etc.
Eh bien, en traçant l'arbre des possibilités pour les listes de perles, c'est clair : quand une perle est 0, elle donne deux branches : 0 et 1; alors que si elle est 1, il n'y a qu'une branche : 0.
À partir de cela, si l'on note un le nombre de branches qui donnent 0 à l'étape n et vn le nombre de branches qui donnent 1, on obtient :
un+1 = un + vn (tout nombre peut être suivi d'un 0)
vn+1 = un (seuls les 0 peuvent être suivis d'un 1)
Bon, les lecteurs attentifs se rendront compte que cette formulation ne tient pas compte du fait que l'on considère des colliers, c'est-à-dire des listes qui bouclent sur elles-mêmes. Mais je verrai ça plus tard (un mathématicien, c'est comme ça : tu lui poses un problème complexe, il répond à un problème plus simple, parce que ça pourra toujours servir, même s'il aurait été préférable de commencer autrement dès le début).
C'est-à-dire qu'on peut affirmer que le nombre de listes de 0 et de 1 qui répondent à la contrainte (hormis en leurs bornes) est un + vn (soit on termine par un 0, soit par un 1).
Alors, pour résoudre le système récurrent, qui est un cas de récurrence mutuelle, c'est simple puisque le système est linéaire (pas de produits ou autres complications). Et pour cela il y a des méthodes.
En l'occurrence :
un+2 = un+1 + vn+1 = un+1 + un
D'où l'équation récurrente d'ordre 2 :
un+2 - un+1 - un = 0
Qui a pour équation caractéristique :
X2 - X - 1 = 0
Dont les solutions sont :
X1 = (1 + √5)/2 et X2 = (1 - √5)/2
Et là on peut exprimer directement un en fonction de u1 à l'aide de la puissance d'une matrice.
Sauf qu'on va prendre un raccourci, parce qu'en chemin on a reconnu que les un correspondaient à la suite de Fibonacci F, plus précisément que un = Fn+1.
Or, si l'on note φ = (1 + √5)/2 et φ' = (1 - √5)/2, on a : Fn = 1/√5 (φn - φ'n).
Déjà cela permet de calculer un et donc un + vn qui, je le rappelle, est le nombre de listes de 0 et de 1 qui répondent à ta construction (hormis la condition de boucle caractéristique des colliers, malheureusement).
Maintenant, grâce à Wikipédia, je me rends compte que la valeur Fn, pour des questions de convergence, c'est l'entier le plus proche de 1/√5 φn.
Cela nous donne une valeur du nombre de listes considérées :
un + vn = un+1 = Fn+2 ≃ (1 + √5)n+2/(2n+2√5)
Alors, tant que je ne me suis pas coltiné le problème du collier en tant que tel (le fait qu'il soit cyclique), cette valeur ne représente qu'une majoration du nombre à trouver.
Mais voici pour comparer :
Valeurs que tu indiques :
2, 2, 2, 3, 3, 5, 5, 8, 9, 14, 16, 26, 31, 49, 64, 99, 133, 209, 291, 455, 657, 1022, 1510, 2359
Valeurs majorantes que je trouve (qui correspondent à la suite de Fibonacci) :
2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584
Bon, ce n'est pas tout à fait ça, mais avoue que cela ressemble, dans la façon de progresser... Avec encore un peu de travail, ça devrait le faire.
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
@Pieyre: Je n'ai pas tout compris, mais pour une fois j'ai compris un peu plus que rien du tout. 
A mon humble niveau, je crois que je me fais des réflexions voisines. Quand je compare mes listes ordonnées de colliers à perles isolées (pour 4 perles, puis pour 5, puis pour 6), je me dis "ça n'a pas l'air bien malin de faire la liste pour 5 perles à partir de celle pour 4, puis la liste pour 6 à partir de celle pour 5, et ainsi de suite". En fait, bien sûr, c'est plus compliqué que ça...
Mais je pense que de telles réflexions ont quand même un intérêt: si on arrive à définir une démarche pour que la liste pour n+1 perles soit un sous-ensemble d'une liste plus vaste construite à partir de la liste pour n perles, eh bien ça peut déjà être très intéressant: on peut filtrer la liste plus vaste sans que ça prenne un temps fou, et ça permet de repousser la limite de calculabilité sensiblement plus loin.
Ainsi, j'ai limité ma liste à 24 perles, parce qu'au départ j'ai bel et bien pris en compte 16.777.216 valeurs (2 puissance 24) et pour chacune d'entre elles j'ai déterminé algorithmiquement quelle était la valeur minimale pour exprimer un collier avec la même suite de bits bouclant sur elle-même et susceptible d'être retournée; ce qui nous fait plein plein plein d'opérations pour 16.777.216 valeurs.
Mais ensuite, je n'ai eu qu'à classer (avec l'utilitaire Unix sort) les colliers obtenus, puis à virer tous les doublons (ce qui est très facile sur une liste classée) pour obtenir ma liste de "seulement" 352.698 colliers. Et c'est à partir de cette liste déjà considérablement réduite de 352.698 colliers différents que j'ai cherché les colliers à perles isolées. Là, pareil, ça faisait plein plein d'opérations pour chaque collier... mais évidemment, plein plein d'opérations sur 352.698 colliers, ça va quand même beaucoup plus vite que si j'avais essayé de faire la même chose avec 16.777.216 valeurs: c'était seulement long (une grosse demi-heure), alors qu'avec les 16.777.216 valeurs ç'aurait été insupportablement long (presque cinquante fois plus long, donc ça aurait représenté plus d'une journée à faire tourner mon processeur).
Ce qui me fait penser qu'un traitement du type itération + filtrage, même si ça fait un peu "système D" en laissant dans un premier temps subsister pas mal de doublons, ça peut déjà permettre d'aller sensiblement plus loin qu'une simple étude systématique de toutes les valeurs envisageables... et donc j'ai bon espoir de parvenir à indiquer des valeurs exactes pour sensiblement plus que 24 perles.
Et ça serait bien que j'aille sensiblement plus loin, puisque j'ai constaté empiriquement le franchissement d'un "seuil de complexification" aux environs de 145 perles: un inventaire exhaustif des seules "générations canoniques" jusqu'à 145 perles permettrait peut-être de comprendre pourquoi.
Donc, je ne lâche pas le morceau. De toute façon, en période de confinement, il est bon d'avoir de quoi s'occuper.
A mon humble niveau, je crois que je me fais des réflexions voisines. Quand je compare mes listes ordonnées de colliers à perles isolées (pour 4 perles, puis pour 5, puis pour 6), je me dis "ça n'a pas l'air bien malin de faire la liste pour 5 perles à partir de celle pour 4, puis la liste pour 6 à partir de celle pour 5, et ainsi de suite". En fait, bien sûr, c'est plus compliqué que ça...
Mais je pense que de telles réflexions ont quand même un intérêt: si on arrive à définir une démarche pour que la liste pour n+1 perles soit un sous-ensemble d'une liste plus vaste construite à partir de la liste pour n perles, eh bien ça peut déjà être très intéressant: on peut filtrer la liste plus vaste sans que ça prenne un temps fou, et ça permet de repousser la limite de calculabilité sensiblement plus loin.
Ainsi, j'ai limité ma liste à 24 perles, parce qu'au départ j'ai bel et bien pris en compte 16.777.216 valeurs (2 puissance 24) et pour chacune d'entre elles j'ai déterminé algorithmiquement quelle était la valeur minimale pour exprimer un collier avec la même suite de bits bouclant sur elle-même et susceptible d'être retournée; ce qui nous fait plein plein plein d'opérations pour 16.777.216 valeurs.
Mais ensuite, je n'ai eu qu'à classer (avec l'utilitaire Unix sort) les colliers obtenus, puis à virer tous les doublons (ce qui est très facile sur une liste classée) pour obtenir ma liste de "seulement" 352.698 colliers. Et c'est à partir de cette liste déjà considérablement réduite de 352.698 colliers différents que j'ai cherché les colliers à perles isolées. Là, pareil, ça faisait plein plein d'opérations pour chaque collier... mais évidemment, plein plein d'opérations sur 352.698 colliers, ça va quand même beaucoup plus vite que si j'avais essayé de faire la même chose avec 16.777.216 valeurs: c'était seulement long (une grosse demi-heure), alors qu'avec les 16.777.216 valeurs ç'aurait été insupportablement long (presque cinquante fois plus long, donc ça aurait représenté plus d'une journée à faire tourner mon processeur).
Ce qui me fait penser qu'un traitement du type itération + filtrage, même si ça fait un peu "système D" en laissant dans un premier temps subsister pas mal de doublons, ça peut déjà permettre d'aller sensiblement plus loin qu'une simple étude systématique de toutes les valeurs envisageables... et donc j'ai bon espoir de parvenir à indiquer des valeurs exactes pour sensiblement plus que 24 perles.
Et ça serait bien que j'aille sensiblement plus loin, puisque j'ai constaté empiriquement le franchissement d'un "seuil de complexification" aux environs de 145 perles: un inventaire exhaustif des seules "générations canoniques" jusqu'à 145 perles permettrait peut-être de comprendre pourquoi.
Donc, je ne lâche pas le morceau. De toute façon, en période de confinement, il est bon d'avoir de quoi s'occuper.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Je m'autocite:
J'avais une idée derrière la tête en disant ça... Je l'ai suivie et je suis parvenu d'une façon algorithmique pas super-élégante mais quand même utilisable à faire des inventaires complets et ordonnés de mes fameuses générations "canoniques" jusqu'à 37 cellules -- ce qui est quand même beaucoup mieux que les 24 cellules qui avaient constitué la limite supérieure avec ma technique algorithmique précédente, qui était encore plus inélégante. Voici le brouillon des résultats que j'ai relevés:
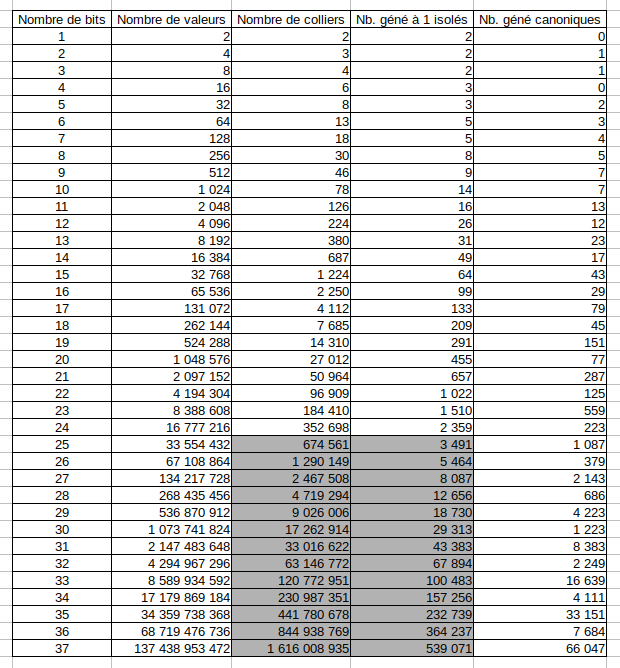
Bon, c'est du brouillon, et quoique je sois certain de mes ordres de grandeur, ça reste perfectible. Toutes les valeurs sur fond grisé ont été déterminées au pifomètre, par simple extrapolation des tendances mesurées sur les lignes placées au-dessus. Les nombres de générations canoniques ont bel et bien été constatés et non estimés, mais cela dit j'ai fait une grosse erreur (sans grande conséquence, mais monumentale), et toutes ces valeurs devraient être majorées de 1, car mes techniques algorithmiques façon "système D" omettent de compter comme génération "canonique" la génération entièrement constituée de 0 -- ce qui est idiot de ma part, mais ne change presque rien aux ordres de grandeur.
On pourra s'étonner que le nombre de générations canoniques évolue de façon très nettement distincte selon que le nombre de bits est pair ou impair (à nombre de bits comparable, il y en a toujours beaucoup plus avec des nombres de bits impairs qu'avec des nombres de bits pairs). C'est dû au fait qu'une génération canonique avec un nombre de bits impair, ça n'a pas exactement la même définition que si le nombre de bits est pair (et ça ne mène pas non plus exactement aux mêmes comportements dans mon automate cellulaire). Ce que je dis n'est pas très clair, même pas dans ma tête d'ailleurs, il faudra que j'y revienne, mais j'avais déjà un peu expliqué ça dans les épisodes précédents, reportez-vous-y (ou laissez-moi dans mon délire si vous préférez).
M'enfin, que le nombre de bits soit pair ou impair, il est clair que le nombre de générations canoniques est quasi-doublé chaque fois qu'on rajoute deux bits, alors que le nombre de colliers est quasi doublé chaque fois qu'on rajoute un bit. Cela confirme ma constatation empirique: à mesure que le nombre de bits augmente, la longueur des tunnels augmente, mais beaucoup moins vite que leur fréquence ne diminue -- donc les tunnels ont des longueurs de plus en plus impressionnantes, mais sont aussi de plus en plus rares et donc de plus en plus difficiles à trouver. C'est la raison pour laquelle je les collectionne.
Pardon, je vous flanque tout ça un peu en vrac, parce que ce fil me sert en fait à prendre des notes. J'expliquerai un peu mieux plus tard... si j'en trouve le temps et l'envie.
Edit et nota: Ma définition la moins foireuse d'une génération canonique se trouve ici.
Petitagore a écrit:si on arrive à définir une démarche pour que la liste pour n+1 perles soit un sous-ensemble d'une liste plus vaste construite à partir de la liste pour n perles, eh bien ça peut déjà être très intéressant: on peut filtrer la liste plus vaste sans que ça prenne un temps fou, et ça permet de repousser la limite de calculabilité sensiblement plus loin.
J'avais une idée derrière la tête en disant ça... Je l'ai suivie et je suis parvenu d'une façon algorithmique pas super-élégante mais quand même utilisable à faire des inventaires complets et ordonnés de mes fameuses générations "canoniques" jusqu'à 37 cellules -- ce qui est quand même beaucoup mieux que les 24 cellules qui avaient constitué la limite supérieure avec ma technique algorithmique précédente, qui était encore plus inélégante. Voici le brouillon des résultats que j'ai relevés:

Bon, c'est du brouillon, et quoique je sois certain de mes ordres de grandeur, ça reste perfectible. Toutes les valeurs sur fond grisé ont été déterminées au pifomètre, par simple extrapolation des tendances mesurées sur les lignes placées au-dessus. Les nombres de générations canoniques ont bel et bien été constatés et non estimés, mais cela dit j'ai fait une grosse erreur (sans grande conséquence, mais monumentale), et toutes ces valeurs devraient être majorées de 1, car mes techniques algorithmiques façon "système D" omettent de compter comme génération "canonique" la génération entièrement constituée de 0 -- ce qui est idiot de ma part, mais ne change presque rien aux ordres de grandeur.
On pourra s'étonner que le nombre de générations canoniques évolue de façon très nettement distincte selon que le nombre de bits est pair ou impair (à nombre de bits comparable, il y en a toujours beaucoup plus avec des nombres de bits impairs qu'avec des nombres de bits pairs). C'est dû au fait qu'une génération canonique avec un nombre de bits impair, ça n'a pas exactement la même définition que si le nombre de bits est pair (et ça ne mène pas non plus exactement aux mêmes comportements dans mon automate cellulaire). Ce que je dis n'est pas très clair, même pas dans ma tête d'ailleurs, il faudra que j'y revienne, mais j'avais déjà un peu expliqué ça dans les épisodes précédents, reportez-vous-y (ou laissez-moi dans mon délire si vous préférez).
M'enfin, que le nombre de bits soit pair ou impair, il est clair que le nombre de générations canoniques est quasi-doublé chaque fois qu'on rajoute deux bits, alors que le nombre de colliers est quasi doublé chaque fois qu'on rajoute un bit. Cela confirme ma constatation empirique: à mesure que le nombre de bits augmente, la longueur des tunnels augmente, mais beaucoup moins vite que leur fréquence ne diminue -- donc les tunnels ont des longueurs de plus en plus impressionnantes, mais sont aussi de plus en plus rares et donc de plus en plus difficiles à trouver. C'est la raison pour laquelle je les collectionne.
Pardon, je vous flanque tout ça un peu en vrac, parce que ce fil me sert en fait à prendre des notes. J'expliquerai un peu mieux plus tard... si j'en trouve le temps et l'envie.
Edit et nota: Ma définition la moins foireuse d'une génération canonique se trouve ici.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
A nouveau, record battu dans ma collection de tunnels: désormais le plus long tunnel de générations paires "naturel" (obtenu à partir d'un mot-graine aléatoire) que l'humanité connaisse a une longueur de 10 138 générations (avec 145 cellules). Le record précédent était de 8 061 générations, également avec 145 cellules.
Je doute qu'il y ait grand-monde parmi les lecteurs de ce fil pour y attacher de l'importance, mais un tunnel de plus de dix mille générations, c'est à l'automate cellulaire Serpicon à peu près ce que le Koh-i Noor est à la joaillerie. Du coup, je vous le montre... sauf qu'il est tellement gros qu'il est inmontrable:

(je serais vous, je ferais un clic droit dessus, puis je demanderais "Afficher l'image"; et il vous faudra probablement zoomer)
Vous vous en contrefoutez, mais c'est quand même historique. A mon avis, ce record-là peut tenir plusieurs années.
Je doute qu'il y ait grand-monde parmi les lecteurs de ce fil pour y attacher de l'importance, mais un tunnel de plus de dix mille générations, c'est à l'automate cellulaire Serpicon à peu près ce que le Koh-i Noor est à la joaillerie. Du coup, je vous le montre... sauf qu'il est tellement gros qu'il est inmontrable:
(je serais vous, je ferais un clic droit dessus, puis je demanderais "Afficher l'image"; et il vous faudra probablement zoomer)
Vous vous en contrefoutez, mais c'est quand même historique. A mon avis, ce record-là peut tenir plusieurs années.
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Oh punaise j'ai rien compris, merci.
Peut être un jour, mais là on est plus dans de l'avant match.
Peut être un jour, mais là on est plus dans de l'avant match.
Seiphys- Messages : 932
Date d'inscription : 07/11/2012
Age : 38

So Sûre 2- Messages : 6805
Date d'inscription : 08/08/2020
Age : 53
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Le monsieur il dit qu'il voit pas le rapport.
Mais bon...c'est pas vraiment grave, enfin peut être un peu chiant. Mais bon qui ne l'est pas ?
Mais bon...c'est pas vraiment grave, enfin peut être un peu chiant. Mais bon qui ne l'est pas ?
Dernière édition par Seiphys le Mar 18 Aoû 2020 - 17:08, édité 1 fois
Seiphys- Messages : 932
Date d'inscription : 07/11/2012
Age : 38
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
La bébéte à cacaKafka aussi , elle fouissait en longs trous .
C'est même le propre ( un comble ) de l'infra humain .
C'est même le propre ( un comble ) de l'infra humain .

limul- Messages : 70
Date d'inscription : 16/08/2020
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Tout est occasion d'apprendre.
Surtout dans "j'aime apprendre", surtout dans ce forum.
Surtout dans "j'aime apprendre", surtout dans ce forum.

So Sûre 2- Messages : 6805
Date d'inscription : 08/08/2020
Age : 53
 Re: Dieu tricote des chaussettes -- et je peux le prouver!
Re: Dieu tricote des chaussettes -- et je peux le prouver!
Oué mais bon, là c'est un fil qui est propre et bien tenu.
Manque de respectsi tu veux je te donne mon avis.
Manque de respect
Seiphys- Messages : 932
Date d'inscription : 07/11/2012
Age : 38
Page 3 sur 4 •  1, 2, 3, 4
1, 2, 3, 4 
 Sujets similaires
Sujets similaires» Je ne cherche pas à prouver que je suis intelligent
» Sortie baskets et chaussettes zébrées
» Pas de titre... seulement un fil qui se déroule! *Ici, câlins gratuits*
» De quoi avez-vous BESOIN, là, tout de suite ?
» Des citations... juste pour se faire du bien
» Sortie baskets et chaussettes zébrées
» Pas de titre... seulement un fil qui se déroule! *Ici, câlins gratuits*
» De quoi avez-vous BESOIN, là, tout de suite ?
» Des citations... juste pour se faire du bien
Page 3 sur 4
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Évènements
Évènements