Qui aime les fractales ?

Passionné par les fractales depuis mon plus jeune âge, je me suis lancé il y a quelque mois dans un projet qui vient enfin d'aboutir.
Il analyse une musique grâce à un réseaux de neurone, et généré une fractale qui varie avec la musique.

Voici la première vidéo générer par mon programme, c'est assez trippant, ya encore des truc à amélioré mais et ce n'est que la première.

bon visionnage.

PS;     à voire en HD

     MATH POWER    

Sympa !

Tu peux expliquer un peu comment tu utilise le neural network pour analyser la musique ?

Prochaine étape les fractales 3D .

LOL j'ai pas envie d'attendre une vie pour le rendu 3D

Pour le réseaux, en gros c'est un mélange de réseaux de kohonen (carte auto adaptative) et de rétro-propagation , chaque neurone de sortie à un spectre de fréquence assigné, à chaque instant le neurone le plus actif va voir son spectre rapprocher du son actuel, et tout les autres éloigné, en parallèle, entre deux frame, on utilise la rétro-propagation pour entraîner les neurones a reconnaître leur spectre et uniquement le leur.
Ainsi chaque neurone de sortie va se spécialiser pour un son particulier et faire en sorte que les autres n'ai pas le même que lui, il vont se répartir équitablement les différent sons récurant dans la musique.

Si sa t' intéresse je peut te filer le code.

Edit: je l'ai coder en C.

Je veux bien, c'est la première fois que j'entends parler de mélanger les self organizing maps et la back propagation.

Tu veut que la partie sur l'analyse audio ou je t'envoi le tout, y a pas mal d'autre truc (j'ai coder mon propre interpréteur, pour coder la fonction de la fractale simplement et la simplifier a bloc)

C'est la partie machine learning qui m’intéresse surtout mais tu peux m'envoyer le tout si tu veux, je ferais le tri.

si tu veut des détails ou des explication sur le code n'hésite pas

Yep, merci .

Il y avait déjà ça là
https://www.zebrascrossing.net/t4638-ici-postez-vos-images-photos-de-fractales-preferees

arrgh désolé je l'avait pas trouver

Génial ! (avec du Igorrr en prime o/)

Salut. Intéressant. Tu utilise un réseau de combien de neurones ? Quelles sont les performances ?

J'ai lu le sujet et en voyant fractales, j'ai immédiatement pensé à l'étude de morpho urbaine en géographie (on utilise beaucoup les fractales pour l'analyse de forme des tissus urbains).
Pour ma part, il ne s'agit pas de fractales à proprement parlé mais par certains côtés ça s'en rapproche.
voila la figure, il faut imaginer que cela représente une ville avec des objets bâtis qui se diluent dans l'espace à mesure que l'on s'éloigne du centre urbain.
Il y a donc deux dimensions, celle de l'espace physique avec un accroissement de l'espacement entre les objets bâtis à mesure que l'on s'éloigne du centre selon une fonction de type puissance ou exp neg à voir et également la taille des objets bâtis qui diminue à l'infini en fonction de la distance au centre.


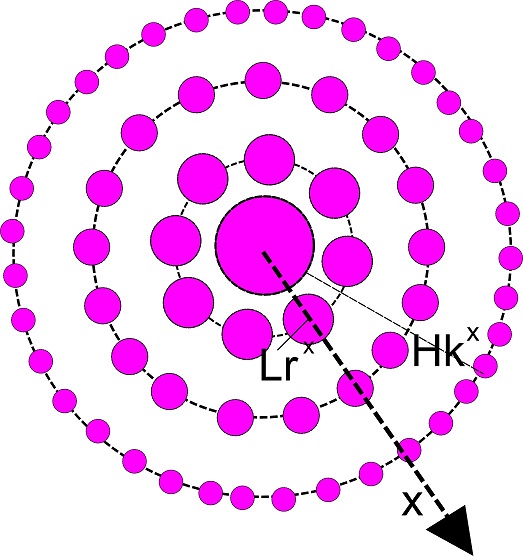
Pour obtenir la densité de bâti pour une distance x du centre, il faut donc déjà calculer la distance x = somme rayon des objets bâtis + somme des inter distances entre les objets bâtis
de l'autre côté, la surface bâtie = somme des rayons des objets bâtis
j'obtiens la formule finale suivante :
Di(x)  = A(1-r^x)*(1/(-B(1-k^x)+A(1-r^x))) = surface bâtie/surface totale
Ca fait donc la forme suivante :


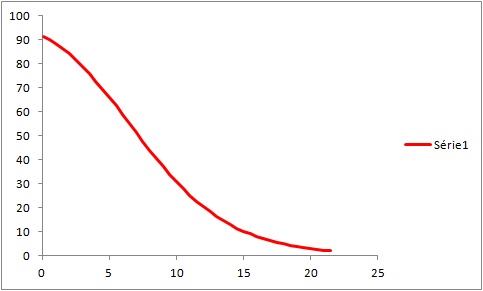
J'attends vos avis éclairés pour ceux qui sont un peu matheux sachant que je me demande si ça vaut le coup de se lancer dans une justification parfaitement abstraite pour une formule statistique. Mais d'un certain côté, je  veux a tout prix éviter de partir sur des stat donc c'est la solution la plus intéressante que j'ai trouvé jusqu’à présent

Vous allez dire, vu la distance avec le sujet initial, j'aurais du faire un autre topic mais ma fois... pourquoi multiplier les sujets quand il y a des points communs.

albius21 a écrit:J'attends vos avis éclairés

ben ... qu'est ce tu essayes de faire au juste ?

stauk a écrit:

albius21 a écrit:J'attends vos avis éclairés

ben ... qu'est ce tu essayes de faire au juste ?

L'idée est simple. On a une fonction logistique dX/dx = -aX(1-X/Xm)) [1] pour modéliser un phénomène géographique qui est celui de la dilution du bâti au sein des espaces périurbains. Cette fonction n'est que statistique et on cherche à la prouver de quelque manière que ce soit.
L'idée est de partir de cette petite démonstration toute bête basée sur une figure géométrique simple censée modéliser le phénomène.
Je suis moins inquiet pour la démonstration en elle même que pour le sens qu'il faut lui donner et le nom qu'il faut lui attribuer.
S'il fallait donner un nom à ce type de transformation géométrique, quel serait il (homothétie, fractales...) ? ma connaissance dans le domaine est insuffisante.
Ensuite, est ce nécessaire de partir sur une construction géométrique pour valider une fonction (ou dans ce cas la prouver justement que cette fonction empirique [1] n'est pas exacte).
Est ce qu'on n'est bien dans le protocole d'une démarche expérimentale sachant que dans un premier temps on a testé des stat, on a ajusté un modèle a priori avec succès pour un panel important de ville ([1]) et ici on montre l'existence de ce modèle sous jacent qui s'accorde avec les stat, ce dernier prend une forme similaire à [1] mais s'exprime différemment. Après est ce que ce nouveau modèle ne peut pas être rapproché de [1] aussi par transformation mathématique, c'est une autre question.

Je n'ai pas eu de réponse à ce jour et je m'interroge. Est ce la nature de la discussion trop spécifique, la trivialité des concepts et de la logique employée ou au contraire la spécificité de l'effort scientifique qui rebute le posteur ?
J'attends vos idées, ce travail est complétement en friche, il n’enthousiasme pas vraiment les foules au travail, pour ainsi dire, comme beaucoup de mes sujets, et du coup je me retrouve une nouvelle fois renvoyé à des études en solitaire sans possibilité de partage.

Et il est vrai que je souhaiterais, avant de m'engager dans un processus d'écriture, en discuter un peu pour cerner les besoins, les difficultés et les contours de l'entreprise.

albius21 a écrit:Est ce la nature de la discussion trop spécifique

Pour moi c'est surtout ça. Et aussi que j'ai pas bien compris ce que tu attendais qu'on te réponde.