Comment faire pour créer une projection en 3d d'un hyper-dodécaèdre ? (120 cell)

Question pour les matheux ou autres balèze en géométrie, ou programmation, j'aimerais faire sur mon logiciel de 3D préféré ceci par exemple :


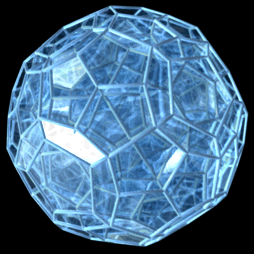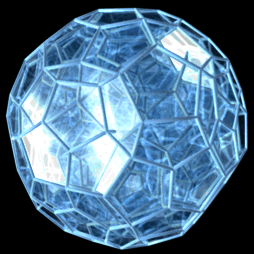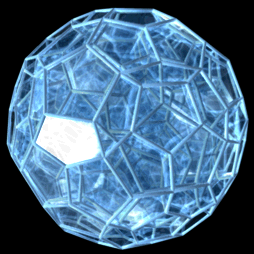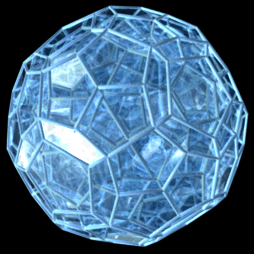
C'est en assemblage de 45 dodécaèdres dont seul le central est régulier, car ces petites saloperie de dodécaèdres pourrait "presque" paver l'espace 3d, mais en fait non, on doit les déformer un petit peu à chaque fois qu'on en rajoute une couche de sorte que les dodécaèdres extérieurs sont très aplatis.
En gros mon problème, c'est de savoir comment les déformer pour avoir un objet harmonieux et comment le faire avec 3dsmax (ou autre chose d'ailleurs) , peut être avec des scripts , mais je ne les maîtrise pas et je serais bien preneur de l'aide de quelqu'un qui saurait par quel bout prendre ce problème.
Peut être en créant un programme qui manipulerait directement un fichier .obj , mais je m'y connais peu en programmation alors...
Je suis pas bien sur de trouver quelqu'un ici que ça intéresse, mais on sait jamais ^^
A votre bon cœur !

pour ma part faire des trucs comme ça, c'est from scratch :

Un code fortran pour générer toutes les coordonnées des points, de la mise en forme VTK / XML (si tu touches) , et finalement Paraview (ou équivalent).

À ce que je comprends, (je ne suis pas spécialiste) c'est un polytope régulier en 4D  (que wikipedia me dit se nommer poétiquement un hécatonicosachore ).
 
Si on prend les coordonnées 4D, et qu'on en fait la projection sur n'importe laquelle des (3 parmi 4 = 4 ) sous-espaces 3D, on aurait des coordonnées de la bête projetée en 3D.
Mais de cette façon, on ne verra pas bien toute la structure...

Donc le diagramme que as mis donne une meilleure idée de la structure (mais sans respecter les longueurs) et ça s'appelle un diagramme de Schlegel...

La méthode pour le dessiner, en gros:  

Une Projection sur l'hypersphère en partant d'un point au milieu , et ensuite seulement faire la projection stéréographique sur un hyperplan.  
L'hypersphere, c'est un espace 3D qui est plongé dans l'espace 4D euclidien de la même manière qu'une sphère 2D l'est dans un espace 3D.
Tous les polyèdres convexes (3D) par exemple peuvent être projetés sur la sphère 2D d'une façon qui préserve la topologie: les faces, les arrêtes, les noeuds restent connectés de la même façon.  C'est analogue pour les polytopes convexes en 4D.

En 4D, chaque hypersphère 3D est une coquille (paramétrée par 3 angles) et située à une distance radiale définie de l'origine.  

Ensuite pour la projection stéréographique, il faudra envoyer  chacun des points de l'hypersphère 3D sur un hyperplan 3D, en suivant les rayons partant du "pôle nord" de la sphère 3D. (on appelle ça la sphère de Riemann habituellement)
C'est le principe de la géométrie projective .   Il faut voir des dessins de l'analogue en 3D pour voir le principe.  Ensuite seulement refaire pareil en 4D. La sphère 4D a quand même une structure plus compliqué que la sphère 3D: ( en particulier on peut la décomposer de manière amusante ), donc il faut se méfier aussi de notre intuition 3D.

Sur wiki, il y a des dessins du même type de diagramme pour des polyèdre 3D projetés en 2D de cette façon, pour s'aider à se faire une intuition de la chose.  
https://fr.wikipedia.org/wiki/Diagramme_de_Schlegel

Et wow , Ici il y de beaux dessins et on nous donne plus d"explications sur comment dessiner cette jolie structure 4D projetée comme j'essayais de dire:  
Mais avouons que des dessins ça aide à suivre.  
http://images.math.cnrs.fr/Comment-dessiner-un.html

Pour ce qui est du détail de l'implémentation pour l'affichage graphique je n'y connais rien, mais naivement je ferais les calculs en matlab et afficherais un graphique relativement laid, mais ça me donnes envie d'apprendre à faire cela en plus beau.

Dans les applications ce pourrait être un réseau d'oscillateurs identiques couplés

Il me semble qu'a mon niveau, faire moi même la projection de l'hyper-dodécaèdre sur une hypersphère puis sur un hyperplan me semble difficile, d'autant qu'il me faudrait les coordonnées 4D de chacun des points de l'hyper-dodécaèdre pour commencer.
J'avais plutôt dans l'idée de tricher, d'autant que je vois à peu près comment c'est construit en 3D, il "suffit" de coller les dodécaèdres face à face et de les emboîter, mais mon problème pour ça, c'est la correction à appliquer aux dodécaèdres qu'on ajoute :

Ici, je dois fusionner 4 vertex qui sont un peu écartés, dans ce cas là, ça peut se faire facilement et de manière régulière, mais plus on ajoute de dodécaèdres, plus ils sont déformés et ça devient difficile de fusionner les points de manière régulière, et aussi de rajouter un dodécaèdre à emboîter car la forme de base s'en éloigne de plus en plus.
D'autant qu'à ce que je comprend, les distances sont arbitraires, comment du coup les choisir ?
Si je pouvais avoir les coordonnées des sommets, j'arriverai à me débrouiller pour connecter tout ça, mais même ça ne me semble pas évident.
Il va falloir que je me plonge dans l'explication dont tu m'as posté le lien, il disent avoir fait les images avec Fragmentarium, ça vaudrait le coup que je m'y intéresse aussi.
En tout cas c'est dingue la somme de connaissance qu'il me faudrait ingérer juste pour arriver à faire un joli objet 3D qui ne me servira à rien à part apaiser ma frustration de ne pas être capable de le faire pour l'instant ! (enfin si je savais comment faire, ça intéresserait pas...)
Et puis l'espace dodécèdrique de Poincaré est peut être la forme de notre univers (http://www.futura-sciences.com/magazines/espace/infos/actu/d/astronomie-notre-univers-il-fini-chiffonne-14540/
Et ça, ça serait vraiment classe ^^

Gwel56 a écrit:Il me semble qu'a mon niveau, faire moi même la projection de l'hyper-dodécaèdre sur une hypersphère puis sur un hyperplan me semble difficile, d'autant qu'il me faudrait les coordonnées 4D de chacun des points de l'hyper-dodécaèdre pour commencer.
J'avais plutôt dans l'idée de tricher, d'autant que je vois à peu près comment c'est construit en 3D, il "suffit" de coller les dodécaèdres face à face et de les emboîter, mais mon problème pour ça, c'est la correction à appliquer aux dodécaèdres qu'on ajoute :
...
Ici, je dois fusionner 4 vertex qui sont un peu écartés, dans ce cas là, ça peut se faire facilement et de manière régulière, mais plus on ajoute de dodécaèdres, plus ils sont déformés et ça devient difficile de fusionner les points de manière régulière, et aussi de rajouter un dodécaèdre à emboîter car la forme de base s'en éloigne de plus en plus.
D'autant qu'à ce que je comprend, les distances sont arbitraires, comment du coup les choisir ?
Si je pouvais avoir les coordonnées des sommets, j'arriverai à me débrouiller pour connecter tout ça, mais même ça ne me semble pas évident.
Il va falloir que je me plonge dans l'explication dont tu m'as posté le lien, il disent avoir fait les images avec Fragmentarium, ça vaudrait le coup que je m'y intéresse aussi.
En tout cas c'est dingue la somme de connaissance qu'il me faudrait ingérer juste pour arriver à faire un joli objet 3D qui ne me servira à rien à part apaiser ma frustration de ne pas être capable de le faire pour l'instant ! (enfin si je savais comment faire, ça intéresserait pas...)
Et puis l'espace dodécèdrique de Poincaré est peut être la forme de notre univers (http://www.futura-sciences.com/magazines/espace/infos/actu/d/astronomie-notre-univers-il-fini-chiffonne-14540/
Et ça, ça serait vraiment classe ^^

Mais ça vaut le coup, ensuite tu pourras faire des casse-tête en 4 dimensions

Bon ta manière d'aborder la question est finalement un peu différent de ce que je suggérais.  Dans le fond, c'est comme si on essayait maintenant de paver l'espace 3D avec des dodécahèdres, mais sans se préoccuper que ceux-ci soient ou non parfaitement réguliers. C'est comme un type de pavage plus général, (et je ne sais pas si des mathématiciens professionels on regardé cela comme ça avant, et s'il y a des résultats pour t'aider à le faire en visualisation graphique). Pour moi, si on cesse de se préoccupper des longueurs des arrêtes et de la régularité des polyèdres, c'est qu'on garde les propriétés topologiques de la structure.  On va coller les 120 celulles n'importe comment en respectant la topologie prescrite.  Je me demande si ce sera équivalent.  Même si on respecte localement la structure de la bête, on n'aura pas vérifié la convexité de la structure 4D.  ( L'animal est supposé être un polytope 4D convexe régulier ) .  Bon, je me demande si on ne pourrait pas introduire une notion de courbure intrinsèque de notre espace 3D comme si il était recourbé en 4D et ensuite s'assurer que cette courbure soit constante pour faire comme si on était vraiment dans une hypersphère 3D ( qui est un espace à courbure constante ). Bon je dis ça, je délire peut-être, mais il y a matière à s'amuser...  

Pour pas se compliquer la vie, on peut aussi simplement appliquer la définition comme je suggérais.
On peut prendre les coordonnées cartésiennes  dans un espace euclidien 4D: elles sont déjà données par exemple ici  
http://mathworld.wolfram.com/120-Cell.html
   
Il y a la liste des 600 sommets de la figure.  En incluant toutes les symétries de permutation, la description tient en quelques lignes..

Faire la projection sur l'hypersphère, ça veut juste dire normaliser, pour chacun des points, les coordonnées cartésiennes de manière à ramener à l'unité la distance radiale entre le pt et l'origine. Donc pour chaque point (x1,x2,x3,x4), on divise le quadruplet par la norme euclidienne  norme= x1^2 + x2^2+ x3^2+ x4^2 .

Ensuite, la projection stéréographique d'une sphère à n-dimension sur un espace euclidien à n dim est donné par

 (image de wikipedia).  

L'application ne va pas préserver les distance, mais la topologie et les angles sont préservés. (C'est une application conforme).

Finalement ça ne semble pas si pire comparativement...    

La méthode de calcul me semble abordable, mais il va falloir automatiser le processus, j'ai trouvé des fichiers avec la liste de toutes les coordonnées des vertex ainsi que des cellules correspondantes en 4D http://meshcompression.org/index.php/random-stuff/11-vertices-and-cells-of-a-120-cell-4d-polychoron, j'imagine que ça doit être possible de de faire un programme qui extrait du fichier les infos, puis qui automatise le calcul pour inserer les données directement dans un fichier .obj
Je crois que je vais faire appel à un pote qui est un peu comme moi à aimer s'acharner sur des trucs inutiles mais qui en plus est meilleur en math et programmation, il suffira d'attiser un peu sa curiosité et il pourrait bien me faire toute la partie galère de codage ^^
Question: est-ce que des dodécaèdres convexes (en3D) impliquent un hyperdodécaèdre 4D convexe ? (d'ailleurs qu'est ce que ça peut bien vouloir dire convexe en 4D ? difficile de se représenter qd même)

Intuitivement j'ai bien l'impression que des dodécaèdres pourrait paver un espace hyperbolique 3D ou un truc du genre, mais je n'ai pas idée de comment définir une telle chose, et encore moins comment l’intégrer dans un logiciel 3D.

Gwel56 a écrit:La méthode de calcul me semble abordable, mais il va falloir automatiser le processus, j'ai trouvé des fichiers avec la liste de toutes les coordonnées des vertex ainsi que des cellules correspondantes en 4D http://meshcompression.org/index.php/random-stuff/11-vertices-and-cells-of-a-120-cell-4d-polychoron, j'imagine que ça doit être possible de de faire un programme qui extrait du fichier les infos, puis qui automatise le calcul pour inserer les données directement dans un fichier .obj
Je crois que je vais faire appel à un pote qui est un peu comme moi à aimer s'acharner sur des trucs inutiles mais qui en plus est meilleur en math et programmation, il suffira d'attiser un peu sa curiosité et il pourrait bien me faire toute la partie galère de codage ^^
Question: est-ce que des dodécaèdres convexes (en3D) impliquent un hyperdodécaèdre 4D convexe ? (d'ailleurs qu'est ce que ça peut bien vouloir dire convexe en 4D ? difficile de se représenter qd même)

Intuitivement j'ai bien l'impression que des dodécaèdres pourrait paver un espace hyperbolique 3D ou un truc du genre, mais je n'ai pas idée de comment définir une telle chose, et encore moins comment l’intégrer dans un logiciel 3D.

J'ai sauvé aussi la page que tu proposes, mais je continue à penser plus simple de génére soit même la liste des sommets. Après tout, il n'y a que quelques points (5 ou 7 ) vraiment distincts, et tous les autres s'obtiennent par symétrie.  Il suffira de faire une panoplie de boucles pour produire toutes les combinaisons décrites. Là tu me donnes envie d'essayer de le faire aussi , au moins pour vérifier si ça marche comme je dis. (Mais j'ai la flemme !)

Pour paver un espace hyperbolique...hmmm  je sais vraiment pas.  La géométrie hyperbolique, ça me semble vraiment un autre sujet, ça connecte peut-être mais pour chercher ça il faudrait pénétrer des articles de maths pures absolument incomprehensibles en dehors d'un cercle restreints d'initiés..

Convexe en 4D, ce n'est plus compliqué qu'en 3D.  C'est juste qu'entre toute paire de points de la surface délimitant le polytope, on peut tracer une droite passant seulement à l'intérieur.   Si il existait une concavité, il y aurait des points tels que la droite les liant serait obligée de sortir à l'extérieur du polytope.  

Pour la question, je vais essayé de répondre: étant donné un polyèdre 3D, peut-on en déduire de manière unique un polytope 4D dont le polyèdre 3D serait la projection qu'on a décrite plus haut.  
La projection stéréographique est bijective. Donc le polyèdre en 3D, on peut le voir dans un hyperplan d'un espace 4D et le mettre en bijection avec une version de lui-même qui serait dans l'hypersphere unité.  On cherche ensuite une structure dans l'espace 4D dont la projection sur l'hypersphere serait le polyèdre 3D.   Projeter de 4D à 3D, c'est réduire l'information, mais pour construire une structure 4D à partir de la structure 3D, ça exige une information supplémentaire.  Si le polytope à reconstruire est supposé suffisamment régulier, on a toute l'information nécessaire (l'hypothèse de régularité est une information qui devrait complèter).


Mais pourquoi tu dis que c'est s'acharner sur des choses inutiles ? Je suis certains qu'il y a des applications. Par exemple, il y a des matériaux formés de quasicristaux. Ça suit une idée analogue: ce sont des structures périodiques dans des espaces de plus de 3 dimensions, et qui deviennent non-périodique en 2D ou 3D. Honnêtement je ne sais pas à quoi ça peut servir, mais c'est une question de physique appliquée.

L’intérêt de la page en lien est surtout qu'elle fournit les cellules correspondantes aux vertex, car effectivement on peut avoir les coordonnées en faisant des permutations, mais on est pas trés avancé ensuite quand il s'agit de reconstituer les faces.

Pour ce qui est de l'espace hyperbolique et du pavage j'avais même pas vu, mais ils en parlent dans le lien que tu m'as filé :
http://images.math.cnrs.fr/Comment-dessiner-un.html

Salut,

Juste un éclaircissement : tu cherches à faire la projection d'un hyper-dodécaèdre ou placer des ensembles de points pour former des dodécaèdres ? Sauf erreur de ma part la projection varie selon l'angle, auquel cas on ne peut avoir un objet 3D figé.
C'est important notamment pour la méthode de calcul et de placement des points (usage ou non de symétries, boucles, etc).

Alors dans l'idéal, je voudrais arriver à réaliser un truc comme ça


sous la forme d'un fichier .obj , et pour ça il me faut arriver à insérer les coordonnées des vertex dans mon fichier, et lier les bons vertex entre eux pour les arrêtes.
Mais j'aurai un autre problème pour faire un rendu, ça sera le diamètre des arrêtes et des joints qui devrait augmenter en fonction de l’éloignement du centre....et ça je vois mal comment faire, car pour passer d'un maillage à un objet comme sur la photo avec des sphères et des cylindres, je pensais passer par un plugin 3ds Max, mais il n'est pas paramettrable et toutes les structures auraient la même taille.
Enfin si déjà j'arrive à l'étape maillage, je serai content.

Au passage, j'ai téléchargé le logiciel Fragmentarium qui manipule des fractales et toutes sortes d'objet mathématiques, et c'est magique, je le conseille vivement, c'est super fun !
http://syntopia.github.io/Fragmentarium/get.html