Les très grands nombres
+7
Badak
Stegos
fift
Tokamak
Asperzebre
Pieyre
holokian
11 participants
Page 1 sur 2
Page 1 sur 2 • 1, 2 
 Les très grands nombres
Les très grands nombres
Je suis fasciné par l'infini et le très grand.
En révassant pour le petit déj, j'ai eu une idée pour trouver des très grands nombres.
Voilà, on a l'addition c'est la base : 2 + 3 = 5. Puis, on utilise l'addition pour créer la multiplication : 2 + 2 + 2 = 3*2. Puis on utilise la multiplication pour créer l'exposant.
On pourrait utiliser l'exposant pour créer, je sais pas, le pix par exemple. 3 pix 5 = 3^(3^(3^(3^3))). Là, on est déjà dans les grandes immensités avec le pix.
Et puis, je me suis dit qu'il fallait généraliser. 1 pour l'addition, 2 pour la multiplication, 3 pour l'exposant, 4 pour le pix et ainsi de suite. On pourrait appeler ça l'ordre de grandeur, et par exemple :
3 o3 2 = 3^2 ; ici o3 vaut l'exposant. Mais forcément 2 o1 2 = 2 + 2.
Mais alors que vaut 3 o4 5, ça vaut 3 pix 5. Mais on peut aller plus loin que vaut 3 o12 4 ? Et 10000 o324 561 ?
(On pourrait même créer des opérateurs d'un ordre de grandeur de niveau englobant (méta), puisque le ox peut se mettre au carré par exemple (4 o5 4), et on pourrait généraliser encore ces ordre de grandeur.)
Bref, revenons à ce que je disais. Sachant qu'un Google = 10^100, qu'un googleplex vaut 10^google. On pourrait trouver le nombre immense googleplex o(googleplex) googleplex.
Voilà, ça sert à rien, mais fallait que ça sorte...
En révassant pour le petit déj, j'ai eu une idée pour trouver des très grands nombres.
Voilà, on a l'addition c'est la base : 2 + 3 = 5. Puis, on utilise l'addition pour créer la multiplication : 2 + 2 + 2 = 3*2. Puis on utilise la multiplication pour créer l'exposant.
On pourrait utiliser l'exposant pour créer, je sais pas, le pix par exemple. 3 pix 5 = 3^(3^(3^(3^3))). Là, on est déjà dans les grandes immensités avec le pix.
Et puis, je me suis dit qu'il fallait généraliser. 1 pour l'addition, 2 pour la multiplication, 3 pour l'exposant, 4 pour le pix et ainsi de suite. On pourrait appeler ça l'ordre de grandeur, et par exemple :
3 o3 2 = 3^2 ; ici o3 vaut l'exposant. Mais forcément 2 o1 2 = 2 + 2.
Mais alors que vaut 3 o4 5, ça vaut 3 pix 5. Mais on peut aller plus loin que vaut 3 o12 4 ? Et 10000 o324 561 ?
(On pourrait même créer des opérateurs d'un ordre de grandeur de niveau englobant (méta), puisque le ox peut se mettre au carré par exemple (4 o5 4), et on pourrait généraliser encore ces ordre de grandeur.)
Bref, revenons à ce que je disais. Sachant qu'un Google = 10^100, qu'un googleplex vaut 10^google. On pourrait trouver le nombre immense googleplex o(googleplex) googleplex.
Voilà, ça sert à rien, mais fallait que ça sorte...

holokian- Messages : 605
Date d'inscription : 11/02/2018
Age : 47
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
le corolaire est que tout infini peut être également ramassé sur lui même
on peut le résumer dans une formule simplifiée pour constater avec cantor que les infinis ont des tailles différentes
pour moi une des plus grandes découvertes en mathématique
bizarrement cela ne semble pas émouvoir le monde
https://www.futura-sciences.com/sciences/dossiers/mathematiques-infini-il-paradoxal-mathematiques-1590/page/5/
"Cantor, toujours occupé à classer les infinis, a en effet découvert avec stupeur que l'ensemble des points d'une surface (un carré, par exemple) possède la même taille que l'ensemble des points d'un segment de droite. Du point de vue de leur taille d'ensemble infini, une droite et un plan (ou même un espace de dimension n) sont identiques. Il écrira à Dedekind à ce propos : « Je le vois, mais je ne le crois pas. »"
https://fr.wikipedia.org/wiki/Georg_Cantor
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Cantor
"On peut également se servir du théorème de Cantor pour montrer qu'il n'existe pas d'ensemble de tous les ensembles (on parle parfois du paradoxe de Cantor, du moins dans une théorie des ensembles qui permet de développer ces notions), puisque celui-ci inclurait l'ensemble de ses parties. "
mais....
http://www.slate.fr/story/151703/mathematiciens-demonstrations-infinis-egaux
"La démonstration que la mathématicienne américaine Maryanthe Malliaris et son homologue israélien Saharon Shelah viennent de publier, qui prouve que deux ensembles mathématiques infinis ont la même taille, était attendue depuis près de 70 ans. Pourtant, elle concerne des nombres connus de tous."
ainsi donc il y aurait des ensembles finis d'infinis, certains de taille différentes et certains de taille identique
on peut en déduire donc que deux infinis de même tailles pourraient être résumés par un ensemble de fonction similaire
mieux finalement les deux infinis ne seraient que deux variantes d'un infini matrice
on peut le résumer dans une formule simplifiée pour constater avec cantor que les infinis ont des tailles différentes
pour moi une des plus grandes découvertes en mathématique
bizarrement cela ne semble pas émouvoir le monde
https://www.futura-sciences.com/sciences/dossiers/mathematiques-infini-il-paradoxal-mathematiques-1590/page/5/
"Cantor, toujours occupé à classer les infinis, a en effet découvert avec stupeur que l'ensemble des points d'une surface (un carré, par exemple) possède la même taille que l'ensemble des points d'un segment de droite. Du point de vue de leur taille d'ensemble infini, une droite et un plan (ou même un espace de dimension n) sont identiques. Il écrira à Dedekind à ce propos : « Je le vois, mais je ne le crois pas. »"
https://fr.wikipedia.org/wiki/Georg_Cantor
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Cantor
"On peut également se servir du théorème de Cantor pour montrer qu'il n'existe pas d'ensemble de tous les ensembles (on parle parfois du paradoxe de Cantor, du moins dans une théorie des ensembles qui permet de développer ces notions), puisque celui-ci inclurait l'ensemble de ses parties. "
mais....
http://www.slate.fr/story/151703/mathematiciens-demonstrations-infinis-egaux
"La démonstration que la mathématicienne américaine Maryanthe Malliaris et son homologue israélien Saharon Shelah viennent de publier, qui prouve que deux ensembles mathématiques infinis ont la même taille, était attendue depuis près de 70 ans. Pourtant, elle concerne des nombres connus de tous."
ainsi donc il y aurait des ensembles finis d'infinis, certains de taille différentes et certains de taille identique
on peut en déduire donc que deux infinis de même tailles pourraient être résumés par un ensemble de fonction similaire
mieux finalement les deux infinis ne seraient que deux variantes d'un infini matrice
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
Bravo Holokian ! Mais cela existe déjà : c'est ce qu'on appelle la Notation des puissances itérées de Knuth, qui peut elle-même être généralisée à des nombres encore plus grands.
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Les très grands nombres
Re: Les très grands nombres
marrant du lien de pieyre
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Goodstein
j'ai déjà vu cela récemment une suite mathématique qui immanquablement se termine par zero quoi qu'on mesure
une fonction en fait
si on prend un nombre pair on additionne.; si on prend un nombre impair on divise si j'ai mémoire...
ah voilà j'ai retrouvé
https://sciencetonnante.wordpress.com/2011/06/27/la-conjecture-de-syracuse/
"L’énoncé de la conjecture
Prenez un nombre entier positif, et appliquez lui le traitement suivant :
s’il est pair, vous le divisez par 2;
s’il est impair, vous le multipliez par 3 et vous ajoutez 1.
"
et c'est pas 0
"La conjecture de Syracuse s’énonce ainsi : quel que soit le nombre que l’on choisisse au départ, on finira par tomber sur 1."
https://mathsyracuse.wordpress.com/
http://www.univ-orleans.fr/mapmo/membres/cordier/centre-galois/doc/syracuse_2012.pdf
"La trajectoire de 27
Certaines trajectoires sont spectaculaires et valent le détour. Celle de
, par exemple, est une montagne
russe qui monte vers des hauteurs inattendues. Mais rien n’y fait, après quelques dizaines d’étapes, vous verrez,
elle retombe sur 1"
27 2+7 9
les particularités des nombres 3 6 9 dans les suite a été identifiée par tesla
on retrouve les mêmes bizarreries dans la suite des nombres premiers qui réduits ne présentent pas une uniformité des 3 6 9
y a quek chose là précisémment
quelque part si on pousse la logique l'absence relative de 3 6 9 dans une suite tendrait à donner un indice sur la taille de son infinité
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Goodstein
j'ai déjà vu cela récemment une suite mathématique qui immanquablement se termine par zero quoi qu'on mesure
une fonction en fait
si on prend un nombre pair on additionne.; si on prend un nombre impair on divise si j'ai mémoire...
ah voilà j'ai retrouvé
https://sciencetonnante.wordpress.com/2011/06/27/la-conjecture-de-syracuse/
"L’énoncé de la conjecture
Prenez un nombre entier positif, et appliquez lui le traitement suivant :
s’il est pair, vous le divisez par 2;
s’il est impair, vous le multipliez par 3 et vous ajoutez 1.
"
et c'est pas 0
"La conjecture de Syracuse s’énonce ainsi : quel que soit le nombre que l’on choisisse au départ, on finira par tomber sur 1."
https://mathsyracuse.wordpress.com/
http://www.univ-orleans.fr/mapmo/membres/cordier/centre-galois/doc/syracuse_2012.pdf
"La trajectoire de 27
Certaines trajectoires sont spectaculaires et valent le détour. Celle de
, par exemple, est une montagne
russe qui monte vers des hauteurs inattendues. Mais rien n’y fait, après quelques dizaines d’étapes, vous verrez,
elle retombe sur 1"
27 2+7 9
les particularités des nombres 3 6 9 dans les suite a été identifiée par tesla
on retrouve les mêmes bizarreries dans la suite des nombres premiers qui réduits ne présentent pas une uniformité des 3 6 9
y a quek chose là précisémment
quelque part si on pousse la logique l'absence relative de 3 6 9 dans une suite tendrait à donner un indice sur la taille de son infinité
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
Wouah, cool de voir que le sujet inspire 
Edit : petite idée en passant, finalement toute opération est une manière de décrire simplement une addition (on peut parler que la complexité de Kolmogorov de l'addition est faible, et peut donc être décrite facilement)
@Hiémale, ça aurait été cool de pouvoir au moins choisir le condiment
@ZebMckay2 : oui c'est fascinant cette idée d'infinis plus grands que les autres.
@Pieyre : ah c'est chouette ça. Finalement, c'est fun de réinventer (mal) la roue
Edit : petite idée en passant, finalement toute opération est une manière de décrire simplement une addition (on peut parler que la complexité de Kolmogorov de l'addition est faible, et peut donc être décrite facilement)
@Hiémale, ça aurait été cool de pouvoir au moins choisir le condiment
@ZebMckay2 : oui c'est fascinant cette idée d'infinis plus grands que les autres.
@Pieyre : ah c'est chouette ça. Finalement, c'est fun de réinventer (mal) la roue

holokian- Messages : 605
Date d'inscription : 11/02/2018
Age : 47
 Re: Les très grands nombres
Re: Les très grands nombres
Ah, j'aime beaucoup, je m'étais amusé à faire un truc du même genre.
J'aimerais vous présenter le plus grand nombre de mon invention, que j’appellerais en toute modestie un Asperzebrium
Le googleplex est ridicule en comparaison.
Si on cherchait à écrire l'Asperzebrium à base de googleplexs: googleplex^googleplex^googleplex^googleplex...l'univers entier ne serait pas suffisant pour écrire ce nombre
Je travaille dans le développement ci dessous uniquement avec des entiers positifs.
Je commence par redéfinir l'addition, de la manière suivante:
Je définis l'addition d'ordre 1, que je note [+1], comme étant l'addition classique:
A[+1]B=A+B
Ensuite, pour tout N >1, je définis l'addition d'ordre N, que je note [+N] de la façon suivante:
A[+N]B = A[+N-1]A[+N-1]A[+N-1]A....B fois. (il doit y avoir moyen de formuler ça plus joliment mathématiquement parlant, mais je n'ai pas trouvé).
Je vous fais les premiers:
A[+2]B=A[+1]A[+1]A[+1]A....B fois = A+A+A...B fois: multiplication classique A*B.
A[+3]B=A[+2]A[+2]A[+2]A...B fois = A*A*A*A...B fois, ou A^B.
A[+4]B=A[+3]A[+3]A...B fois = A^A^A...B fois
Un problème survient ici, c'est la priorité des opérateurs, qui n'est pas à ma connaissance définie pour les exponentielles (ça ne me surprendrait pas du tout que ce soit défini, mais j'ignore la règle à appliquer).
Ainsi, on a le choix entre:
3^3^3= 3^(3^3) = 3^27 = 7625597484987
3^3^3=(3^3)^3=27^3 = 19683, ce qui n'est pas du tout pareil.
Le but étant de faire un grand nombre, on prendra la 1ère solution, quitte à redéfinir si nécessaire l'addition d'ordre N en utilisant des parenthèses afin de faire les opérations dans l'ordre souhaité.
On a ensuite A[+5]B=A[+4]A[+4]A[+4]A....B fois
A[+6]B=A[+5]A[+5]A[+5]A...B fois
et ainsi de suite.
Ceci étant défini, et je l'espère clair pour tout le monde, nous allons maintenant faire une suite de nombres, que je nommerais U0 (le 0 a son importance, on y reviendra plus tard), définie de la façon suivante:
U0(0)=10[+10]10. (restons modeste, pas besoin d'aller chercher dans les 99999999, 10 sera très bien comme nombre de base)
Pour tout N > 0, U0(N)= U0(N-1)[+U0(N-1)]U0(N-1)
Ainsi, U0(1)=U0(0)[+U0(0)]U0(0)
U0(2)=U0(1)[+U0(1)]U0(1)
U0(3)=U0(2)[+U0(2)]U0(2)
et ainsi de suite.
Je vais maintenant définir d'autres suites, en faisant une récursion sur le nom de la suite.
Pour tout entier positif k, et tout entier positif ou nul j, tels que j = k-1, je définis la suite Uk de la façon suivante:
Uk(0)= Uj(Uj(0))
Et de la même façon que pour U0:
Pour tout N > 0, Uk(N)= Uk(N-1)[+Uk(N-1)]Uk(N-1)
Pour rendre ça plus compréhensible, voici quelques exemples:
U1(0)=U0(U0(0))
U1(6)=U1(5)[+U1(5)]U1(5)
U2(0)=U1(U1(0))
U2(3)=U2(2)[+U2(2)]U2(2)
U3(0)=U2(U2(0))
Et ainsi de suite.
J'en arrive à la dernière étape, et tout comme au début je vais rester modeste en utilisant 10 au lieu de 999999...
Posons A=U10(10).
Un Asperzebrium = UA(10), tout simplement
Je m'avoue totalement incapable d'imaginer à quel point c'est gigantesque: rien que le U0(0) = 10[+10]10 est un défi pour l'imagination, et le U0(1) est totalement hors de ma portée.
Voilà, ça sert à rien, mais fallait que ça sorte
J'aimerais vous présenter le plus grand nombre de mon invention, que j’appellerais en toute modestie un Asperzebrium
Le googleplex est ridicule en comparaison.
Si on cherchait à écrire l'Asperzebrium à base de googleplexs: googleplex^googleplex^googleplex^googleplex...l'univers entier ne serait pas suffisant pour écrire ce nombre
Je travaille dans le développement ci dessous uniquement avec des entiers positifs.
Je commence par redéfinir l'addition, de la manière suivante:
Je définis l'addition d'ordre 1, que je note [+1], comme étant l'addition classique:
A[+1]B=A+B
Ensuite, pour tout N >1, je définis l'addition d'ordre N, que je note [+N] de la façon suivante:
A[+N]B = A[+N-1]A[+N-1]A[+N-1]A....B fois. (il doit y avoir moyen de formuler ça plus joliment mathématiquement parlant, mais je n'ai pas trouvé).
Je vous fais les premiers:
A[+2]B=A[+1]A[+1]A[+1]A....B fois = A+A+A...B fois: multiplication classique A*B.
A[+3]B=A[+2]A[+2]A[+2]A...B fois = A*A*A*A...B fois, ou A^B.
A[+4]B=A[+3]A[+3]A...B fois = A^A^A...B fois
Un problème survient ici, c'est la priorité des opérateurs, qui n'est pas à ma connaissance définie pour les exponentielles (ça ne me surprendrait pas du tout que ce soit défini, mais j'ignore la règle à appliquer).
Ainsi, on a le choix entre:
3^3^3= 3^(3^3) = 3^27 = 7625597484987
3^3^3=(3^3)^3=27^3 = 19683, ce qui n'est pas du tout pareil.
Le but étant de faire un grand nombre, on prendra la 1ère solution, quitte à redéfinir si nécessaire l'addition d'ordre N en utilisant des parenthèses afin de faire les opérations dans l'ordre souhaité.
On a ensuite A[+5]B=A[+4]A[+4]A[+4]A....B fois
A[+6]B=A[+5]A[+5]A[+5]A...B fois
et ainsi de suite.
Ceci étant défini, et je l'espère clair pour tout le monde, nous allons maintenant faire une suite de nombres, que je nommerais U0 (le 0 a son importance, on y reviendra plus tard), définie de la façon suivante:
U0(0)=10[+10]10. (restons modeste, pas besoin d'aller chercher dans les 99999999, 10 sera très bien comme nombre de base)
Pour tout N > 0, U0(N)= U0(N-1)[+U0(N-1)]U0(N-1)
Ainsi, U0(1)=U0(0)[+U0(0)]U0(0)
U0(2)=U0(1)[+U0(1)]U0(1)
U0(3)=U0(2)[+U0(2)]U0(2)
et ainsi de suite.
Je vais maintenant définir d'autres suites, en faisant une récursion sur le nom de la suite.
Pour tout entier positif k, et tout entier positif ou nul j, tels que j = k-1, je définis la suite Uk de la façon suivante:
Uk(0)= Uj(Uj(0))
Et de la même façon que pour U0:
Pour tout N > 0, Uk(N)= Uk(N-1)[+Uk(N-1)]Uk(N-1)
Pour rendre ça plus compréhensible, voici quelques exemples:
U1(0)=U0(U0(0))
U1(6)=U1(5)[+U1(5)]U1(5)
U2(0)=U1(U1(0))
U2(3)=U2(2)[+U2(2)]U2(2)
U3(0)=U2(U2(0))
Et ainsi de suite.
J'en arrive à la dernière étape, et tout comme au début je vais rester modeste en utilisant 10 au lieu de 999999...
Posons A=U10(10).
Un Asperzebrium = UA(10), tout simplement
Je m'avoue totalement incapable d'imaginer à quel point c'est gigantesque: rien que le U0(0) = 10[+10]10 est un défi pour l'imagination, et le U0(1) est totalement hors de ma portée.
Voilà, ça sert à rien, mais fallait que ça sorte
Dernière édition par Asperzebre le Mer 7 Mar 2018 - 15:52, édité 1 fois (Raison : erreur parentheses)

Asperzebre- Messages : 2355
Date d'inscription : 10/05/2016
 Re: Les très grands nombres
Re: Les très grands nombres
Il y a eu de l'animation pendant que j'écrivais mon message.
Je n'aurais pas cru qu'un tel sujet attirerait grand monde, je suis agréablement surpris.
Je n'ai pas encore été regarder, mais je ne serais pas étonné que ma redéfinition de l'addition ressemble fort à la notation des puissances itérées dont Pieyre a fait mention.
Je n'aurais pas cru qu'un tel sujet attirerait grand monde, je suis agréablement surpris.
Je n'ai pas encore été regarder, mais je ne serais pas étonné que ma redéfinition de l'addition ressemble fort à la notation des puissances itérées dont Pieyre a fait mention.

Asperzebre- Messages : 2355
Date d'inscription : 10/05/2016
 Re: Les très grands nombres
Re: Les très grands nombres
Tout ça m'évoque un théorème que je ne peux pas prouver, mais qui me semble évident.
Tout opération est un algorithme pour décrire un nombre. On peut donc déduire la complexité de Kolmogorov d'un très grand nombre. Si l'opération est courte, c'est que sa complexité est faible, et si c'est long, sa complexité est grande disons.
Voilà le théorème : la complexité de Kolmogorov d'un grand nombre tend vers l'infini, quand le nombre lui-même tend vers l'infini.
Dit autrement, on aura beau trouver tous les subterfuges du monde, le nombre qu'on trouvera sera infiniment petit par rapport à d'autres nombres. Au bout d'un moment, on ne pourra plus décrire de grands nombres en 10 caractères. Il arrivera forcément un moment où pour décrire un plus grand nombre il faudra un plus grand nombre de caractères... Et ce nombre de caractères finira par tendre vers l'infini.
@Asperzebre : c'est marrant, parce qu'on dirait qu'on a eu la même idée. Sauf que toi tu l'as plus formalisé et tu es allé plus loin. Bravo
Edit : en poussant un peu plus la compréhension jusqu'au bout, c'est assez génial ton truc Asperzebre.
Tout opération est un algorithme pour décrire un nombre. On peut donc déduire la complexité de Kolmogorov d'un très grand nombre. Si l'opération est courte, c'est que sa complexité est faible, et si c'est long, sa complexité est grande disons.
Voilà le théorème : la complexité de Kolmogorov d'un grand nombre tend vers l'infini, quand le nombre lui-même tend vers l'infini.
Dit autrement, on aura beau trouver tous les subterfuges du monde, le nombre qu'on trouvera sera infiniment petit par rapport à d'autres nombres. Au bout d'un moment, on ne pourra plus décrire de grands nombres en 10 caractères. Il arrivera forcément un moment où pour décrire un plus grand nombre il faudra un plus grand nombre de caractères... Et ce nombre de caractères finira par tendre vers l'infini.
@Asperzebre : c'est marrant, parce qu'on dirait qu'on a eu la même idée. Sauf que toi tu l'as plus formalisé et tu es allé plus loin. Bravo
Edit : en poussant un peu plus la compréhension jusqu'au bout, c'est assez génial ton truc Asperzebre.
Dernière édition par holokian le Mer 7 Mar 2018 - 15:16, édité 2 fois

holokian- Messages : 605
Date d'inscription : 11/02/2018
Age : 47
Invité- Invité
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
Tout dépend du langage que l'on utilise. Si l'on admet un nombre infini de symboles de constantes, c'est faux; de même un nombre infini de symboles de fonctions ou d'opérations. Mais, à part ça, ton théorème a toute l'apparence d'être vrai. Reste qu'il y a des propositions indécidables qui affirment que tous les nombres entiers vérifient telle propriété. Dans certaines théories elles sont vraies, mais dans d'autres il existe un premier entier qui ne les vérifient pas, qui peut être aussi grand qu'on le veut (selon les axiomes que l'on choisit, en s'en accordant là aussi possiblement un nombre infini) pour la même proposition. C'est dire qu'un tel théorème ne peut être vrai qu'en précisant soigneusement le contexte formel dans lequel on l'exprime.holokian :
Voilà le théorème : la complexité de Kolmogorov d'un grand nombre tend vers l'infini, quand le nombre lui-même tend vers l'infini.
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Les très grands nombres
Re: Les très grands nombres
@Hiémale : tant que la boutade ne te monte pas au nez... pardon à la tête, il n'y a pas de souci 
@Pieyre : j'ai des notions sur l'idée de proposition indécidable et autres énoncés indémontrables, mais là j'admets que je suis pas assez calé pour le détail. Ceci dit je comprends dans sa globalité/intuitivement la problématique que tu soulèves.
@AelSter : je ne suis pas sûr de comprendre ta demande. Je crois que ce qui est surprenant avec cette suite, c'est qu'on finit toujours par tomber sur 1 alors que sa progression semble a priori un peu hasardeuse. (si j'ai bien tout compris)
@Pieyre : j'ai des notions sur l'idée de proposition indécidable et autres énoncés indémontrables, mais là j'admets que je suis pas assez calé pour le détail. Ceci dit je comprends dans sa globalité/intuitivement la problématique que tu soulèves.
@AelSter : je ne suis pas sûr de comprendre ta demande. Je crois que ce qui est surprenant avec cette suite, c'est qu'on finit toujours par tomber sur 1 alors que sa progression semble a priori un peu hasardeuse. (si j'ai bien tout compris)

holokian- Messages : 605
Date d'inscription : 11/02/2018
Age : 47
 Re: Les très grands nombres
Re: Les très grands nombres
Holokian, c'était juste pour relativiser ce qu'on appelle un théorème. Dans l'arithmétique de Peano, l'ensemble des expressions de longueur au plus égale à n ne peut prendre qu'un nombre fini de valeurs. Il suffit donc de considérer le maximum de ces valeurs et d'y ajouter 1 pour être sûr qu'on ne puisse atteindre cette nouvelle valeur qu'avec une expression de longueur au moins égale à n + 1. Il me semble que cela prouve ton théorème dans ce cadre.
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
 Re: Les très grands nombres
Re: Les très grands nombres
Oui je comprends mieux Pieyre. C'est vrai que j'ai pas défini de cadre à mon "théorème". Effectivement, nombre c'est un peu large, entier naturel eut été plus explicite par exemple.

holokian- Messages : 605
Date d'inscription : 11/02/2018
Age : 47
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
Il y a un concurrent et non des moindres. ^^Asperzebre a écrit:Je m'avoue totalement incapable d'imaginer à quel point c'est gigantesque
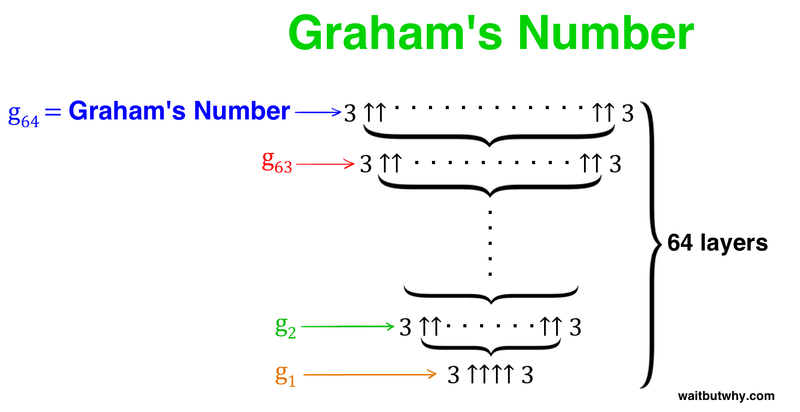
https://waitbutwhy.com/2014/11/1000000-grahams-number.html
Tout simplement ... ... ... y a pas de mot, dans aucune langue.
Même inimaginable c’est trop faible.

- Spoiler:
Et TREE(3) est de trèèèèèèès loin encore plus grand.
« A nesting of depth G64 ? No, that would not even be close ! We don’t know a good bound for TREE(3) in terms of that “g-nesting”, but it has been shown that even a nest of depth G187196 would be much smaller than TREE(3) (that’s the best bound that has ever been proven). »
https://www.quora.com/How-could-you-compare-Grahams-number-with-TREE-3-in-layman-terms-like-g-g-g-g64-with-a-nesting-depth-of-g64-would-that-be-close-to-TREE-3
https://www.quora.com/Is-Tree-3-bigger-than-Graham’s-number
edit : une ch’tite faute s’était glissée.
Dernière édition par Tokamak le Jeu 8 Mar 2018 - 22:32, édité 1 fois

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Les très grands nombres
Re: Les très grands nombres
Intéressant.
Le g du graham est à peu de choses près la même chose que ma suite U0 (en plus petit car il utilise les puissances de 3 et moi les puissances de 10, mais on pourrait faire la comparaison avec une version 'supérieure' du graham, utilisant la puissance de 10).
Mon itération sur le [+U0(N)] ayant un principe similaire à celle permettant de passe de g1 à g2, puis à g3 et ainsi de suite.
Sauf que lui, s'arrête à g(64), le nombre de graham (en version base 10 au lieu de base 3) correspond donc à mon U0(64).
Hors, mon U1(0) est égal à mon U0(U0(0)), c'est à dire un nombre superieur à U0(googleplex).
Graham est déjà un tout petit joueur à côté de mon U1(0), et U1(0) est un stade très peu avancé de mon développement.
Je regarderais plus tard le tree 3, g-g-g-g-g-g64 me semble se rapprocher un peu plus de l'esprit de mon nombre, tout en y restant inférieur.
Le mien serait plutôt (une 'infinité' de g) 64
Le g du graham est à peu de choses près la même chose que ma suite U0 (en plus petit car il utilise les puissances de 3 et moi les puissances de 10, mais on pourrait faire la comparaison avec une version 'supérieure' du graham, utilisant la puissance de 10).
Mon itération sur le [+U0(N)] ayant un principe similaire à celle permettant de passe de g1 à g2, puis à g3 et ainsi de suite.
Sauf que lui, s'arrête à g(64), le nombre de graham (en version base 10 au lieu de base 3) correspond donc à mon U0(64).
Hors, mon U1(0) est égal à mon U0(U0(0)), c'est à dire un nombre superieur à U0(googleplex).
Graham est déjà un tout petit joueur à côté de mon U1(0), et U1(0) est un stade très peu avancé de mon développement.
Je regarderais plus tard le tree 3, g-g-g-g-g-g64 me semble se rapprocher un peu plus de l'esprit de mon nombre, tout en y restant inférieur.
Le mien serait plutôt (une 'infinité' de g) 64
Dernière édition par Asperzebre le Jeu 8 Mar 2018 - 21:49, édité 1 fois (Raison : erreurs parenthèses)

Asperzebre- Messages : 2355
Date d'inscription : 10/05/2016
 Re: Les très grands nombres
Re: Les très grands nombres
Attention aux infinités. 
Oui sur le principe ça ressemble à ta méthode.
Et pour qu’un nombre soit pris en considération, il doit se calquer sur une approche mathématique telle que pour le Nombre de Graham avec les hypercubes etc, il doit être ‘utile’, avoir un ‘but en soi’. Sinon c’est la porte ouverte à toutes les fenêtres.
Oui sur le principe ça ressemble à ta méthode.
Et pour qu’un nombre soit pris en considération, il doit se calquer sur une approche mathématique telle que pour le Nombre de Graham avec les hypercubes etc, il doit être ‘utile’, avoir un ‘but en soi’. Sinon c’est la porte ouverte à toutes les fenêtres.
- par ex tree(3):

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Les très grands nombres
Re: Les très grands nombres
oui, j'ai mis 'infinités' entre guillemets pour cette raison, c'est une façon de parler pour dire un nombre très grand, mais l'Asperzebrium n'est pas à proprement parler une infinité de g: c'est un nombre fini.

Asperzebre- Messages : 2355
Date d'inscription : 10/05/2016
 Re: Les très grands nombres
Re: Les très grands nombres
Le mien est encore plus grand, c’est le tien +1 

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Les très grands nombres
Re: Les très grands nombres
on peut toujours faire plus grand, c'est le principe.
Tout aussi grand qu'il soit, on peut trouver 'infiniment' plus grand que mon nombre
Tout aussi grand qu'il soit, on peut trouver 'infiniment' plus grand que mon nombre

Asperzebre- Messages : 2355
Date d'inscription : 10/05/2016
 Re: Les très grands nombres
Re: Les très grands nombres
Ce qui est difficile, c'est de trouver un nombre plus grand d'un "ordre de grandeur" qu'on n'a pas encore trouvé jusque là.
EDIT : j'ai peut être une idée.
On pourrait généraliser, le passage de UA(10) = B ; UB(10) = C ; UC(10) = E. Et au lieu de l'écrire comme ça, je pose une nouvelle lettre, (tiens le H de holokian tiens ).
).
Donc H(1) = UA(10) ; H(2) = UB(10) ; H(3) = UC(10). Alors le Holokianium = H(10)
(bon c'était facile, j'admets, mais c'était marrant à faire)
EDIT 2 : super la vidéo Tokamak sur TREE(3)
EDIT : j'ai peut être une idée.
On pourrait généraliser, le passage de UA(10) = B ; UB(10) = C ; UC(10) = E. Et au lieu de l'écrire comme ça, je pose une nouvelle lettre, (tiens le H de holokian tiens
Donc H(1) = UA(10) ; H(2) = UB(10) ; H(3) = UC(10). Alors le Holokianium = H(10)
(bon c'était facile, j'admets, mais c'était marrant à faire)
EDIT 2 : super la vidéo Tokamak sur TREE(3)

holokian- Messages : 605
Date d'inscription : 11/02/2018
Age : 47
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
AelSter a écrit:
La suite de Syracuse de n'importe quel nombre entier naturel du système décimal nous conduit vers 1, avant de repartir sur le cycle trivial...
Assez précis comme ça ? ça va ?
Oui
AelSter a écrit:
Par ailleurs, quel est l'intérêt de contredire quelqu'un sans le corriger ou même l'aider, si l'on a les moyens de le faire ?
Ben vu que vous l'avez corrigé tout seul, il y avait un intérêt. Quel est l’intérêt d'éviter de faire réfléchir les gens ?
AelSter a écrit:
C'est juste une question rhétorique...
Non, de vocabulaire et de maths.
Mais effectivement, quitte à être sur un forum de sciences de gens prétendument intelligents parlant de maths, la rigueur, OSEF.
Invité- Invité
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
AelSter a écrit:
Il a été défini la suite "convergente ou divergente" de telle façon : on le sait ou on ne le sait pas. Par la réflexion, il est impossible de le deviner. L'erreur n'est donc pas surprenant de la part d'un néophyte, et je comprends que cela agasse le spécialiste. Donc pour cela, mea culpa.
Ha mais aucun soucis, je ne faisais que relever une erreur (de vocabulaire / convention, peu importe), c'est tout, pas de quoi remuer ciel et terre... :-)
AelSter a écrit:
Sauf qu'il y a des putains de boucles, et pour que ça ait un minimum de gueule, faudrait être capable de dire "quand" ça va tomber sur 1. Et là, j'ai pu voir la juste mesure du problème... Si j'arrive à faire une démonstration sur ces fameux cycles, je publierais sûrement quelque chose, mais ça me semble plus ardu que je le soupçonnais...
C'est juste que des spécialistes qui s'y sont cassés les dents, il y en a eu une quantité impressionnante. Donc prétendre démontrer ça de la part d'un "néophyte" pour reprendre le terme, me parait quelque peu voué à l'échec.
Invité- Invité
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
C'est plus que s'intéresser à ce genre de problème, c'est très bien (clairement il y a de quoi apprendre plein, plein de choses super intéressantes), mais prétendre la solutionner, et/ou l'étudier dans ce but, ça ne peut qu’être source de déception...
Invité- Invité
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
J'ai donc mal interprété vos intentions, au temps pour moi ;-)
Invité- Invité
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
Un interlude durant l’entracte.
Ou quand 1+2+3+4+5+... = -1/12
Ou pas.
Ou bien ça dépend du contexte.
Ou quand 1+2+3+4+5+... = -1/12
Ou pas.
Ou bien ça dépend du contexte.
- Spoiler:
- Spoiler:

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Les très grands nombres
Re: Les très grands nombres
Un autre point de vue sur les très grands nombres Encore une autre manière de dépasser le nombre de Graham :

holokian- Messages : 605
Date d'inscription : 11/02/2018
Age : 47
 Re: Les très grands nombres
Re: Les très grands nombres
En haut du podium il y a le Nombre de Rayo.
http://web.mit.edu/arayo/www/bignums.html
Le nombre de Rayo est un grand nombre défini par Augustín Rayo, qui est réputé être le plus grand nombre spécifiquement nommé. Il fut défini à l'occasion d'un « duel de grands nombres » au MIT le 26 janvier 2007.
Le nombre de Rayo est une version non paradoxale de l'entier intervenant dans le paradoxe de Berry (on peut aussi le voir comme une formalisation de la notion, due à Émile Borel, de « nombre inaccessible »). Il correspond à la description suivante :
« Le plus petit entier supérieur à tout entier définissable par une expression du langage du premier ordre de la théorie des ensembles comportant moins d'un gogol (10E100) de symboles. »
Rayo a donné une forme rigoureuse de cette définition (nécessaire pour satisfaire aux conditions du duel, et en particulier pour montrer que l'entier en question est bien défini dans la théorie ZFC) à l'aide d'une formule du second ordre.
Dans un article qui a inspiré le duel du MIT, Who Can Name the Bigger Number?, Scott Aaronson explore certaines autres méthodes pour définir de très grands nombres (et rappelle au passage que le paradoxe de Berry ne permet de définir rien de précis).
Son analyse a donné à Rayo l'idée de sa construction ; bien que ce ne soit pas immédiatement clair (parce que les notations utilisées pour définir les grands nombres usuels abrègent beaucoup les expressions du langage des prédicats qui en sont les définitions rigoureuses), le nombre de Rayo dépasse (énormément) tout nombre exprimable de façon rigoureuse dans le langage mathématique sans utiliser une construction analogue, par exemple le nombre de Graham G, les nombres définis par la fonction TREE, ou même la valeur de la fonction du castor affairé pour une machine de Turing à TREE (G) états.
https://fr.wikipedia.org/wiki/Nombre_de_Rayo
http://web.mit.edu/arayo/www/bignums.html

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Les très grands nombres
Re: Les très grands nombres
Pour revenir à des nombres plus petits mais déjà gigantesques (et qui peuvent encore s’écrire sous forme de puissances) comme le googolplex (ou gogolplex). Si l’Univers (au-delà de l’Univers observable) restait homogène sur une distance équivalente au googolplex en m (courbure hors concours:) il existerait quantité de copies exactes de nous-mêmes (et tout ce qui nous entoure) au détail près, et d’autres avec des nuances plus ou moins marquées. En ce sens qu’il existe un nombre fini d’états quantiques, différentes manières d’organiser la matière, atomes etc dans un volume comme une enveloppe corporelle. Et ce nombre (déjà énorme) est de loin inférieur au googolplex. Explications https://youtu.be/8GEebx72-qs?t=3m46s

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Les très grands nombres
Re: Les très grands nombres
Tokamak a écrit:Un interlude durant l’entracte.
Ou quand 1+2+3+4+5+... = -1/12
Ou pas.
Ou bien ça dépend du contexte.
- Spoiler:
- Spoiler:
Ou le bien connu 1=2
(en partant de x2 - x 2 = x2 - x2)
fift- Messages : 8855
Date d'inscription : 26/04/2016
Age : 48
Localisation : Paris
 Re: Les très grands nombres
Re: Les très grands nombres
Sauf que là fift - aussi bizarre que cela puisse paraître - ça se tient.
Tout au moins en Physique c’est le cas (par ex effet Casimir).
Tout au moins en Physique c’est le cas (par ex effet Casimir).

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Les très grands nombres
Re: Les très grands nombres
Tokamak a écrit:Sauf que là fift - aussi bizarre que cela puisse paraître - ça se tient.
Tout au moins en Physique c’est le cas (par ex effet Casimir).
Hein ?? Mathématiquement c'est juste faux. Je ne vois pas comment il pourrait en etre autrement "en physique"...
Dernière édition par hobb le Lun 26 Mar 2018 - 19:24, édité 1 fois
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
Bah vi, t’as jeté un oeil aux premières vidéos ?

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Les très grands nombres
Re: Les très grands nombres
Oui, mais je ne vois pas ce que vient faire la sommation de Ramanujan dans l'effet Casimir.
PS : ce n'est pas demain la veille que je prendrai au serieux une vidéo question sciences...
PS : ce n'est pas demain la veille que je prendrai au serieux une vidéo question sciences...
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
Nope.
1+2+3+... ne converge pas, mais diverge vers +∞,
pourquoi, parce que 1-1+1-1+1-.. c'est PAS égal à 1/2
L'explication est là. https://plus.maths.org/content/infinity-or-just-112
C'est pas parce qu'un "youtuber" ne comprend pas ce qu'à écrit Srinivasa Ramanujan, qu'il le sort du contexte, et MÊME si ça passe à la TV ou dans la presse que ça devient vrai
1+2+3+... ne converge pas, mais diverge vers +∞,
pourquoi, parce que 1-1+1-1+1-.. c'est PAS égal à 1/2
L'explication est là. https://plus.maths.org/content/infinity-or-just-112
C'est pas parce qu'un "youtuber" ne comprend pas ce qu'à écrit Srinivasa Ramanujan, qu'il le sort du contexte, et MÊME si ça passe à la TV ou dans la presse que ça devient vrai

Stegos- Messages : 4567
Date d'inscription : 18/02/2018
Age : 105
Localisation : 3ème planète autour du soleil
 Re: Les très grands nombres
Re: Les très grands nombres
Je rajouterai que si on fait RIGOUREUSEMENT la démo prétendue, on obtient ce que dit Stegos : + l'infini. Lors de la démo il y a une erreur manifeste (l'erreur est que si on applique au rasoir cette démonstration, on retranche une infinité de fois plus de terme que la suite en a, ça devient indéfini). J'ai refais la démo correctement sur un coin de table, on obtient bien 1+2+3+... = infini.
Et je ne vois du coup toujours pas ce que ça vient faire dans l'effet Casimir. Si vous parlez d'une somme infinie de fonctions sinus (ou cosinus), c'est simplement une transformée de Fourier, et nulle part cette aberration mathématique n'intervient. De toutes façons cette TF est de carré sommable, donc on n'a pas ce genre de soucis.
Et je ne vois du coup toujours pas ce que ça vient faire dans l'effet Casimir. Si vous parlez d'une somme infinie de fonctions sinus (ou cosinus), c'est simplement une transformée de Fourier, et nulle part cette aberration mathématique n'intervient. De toutes façons cette TF est de carré sommable, donc on n'a pas ce genre de soucis.
Dernière édition par hobb le Lun 26 Mar 2018 - 19:46, édité 1 fois
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
Bon il y avait un spoiler dans le spoiler, personne ne l’a vu ?
Et pour l’effet Casimir c’est expliqué dans l’une des premières vidéos je sais plus laquelle.
Et pour l’effet Casimir c’est expliqué dans l’une des premières vidéos je sais plus laquelle.

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Les très grands nombres
Re: Les très grands nombres
Tokamak a écrit:
Et pour l’effet Casimir c’est expliqué dans l’une des premières vidéos je sais plus laquelle.
Au risque de me (nous) répéter, ce n'est pas parce que quelqu'un n'a rien compris et en fait une vidéo pour étaler son ignorance que cette vidéo a une quelconque pertinence scientifique.
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
Sais-tu qui sont ces deux gars dans les premières vidéos ?
Au LHC ils embauchent vraiment n’importe qui.
En Physique cette équivalence fonctionne.
Au LHC ils embauchent vraiment n’importe qui.
En Physique cette équivalence fonctionne.

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Les très grands nombres
Re: Les très grands nombres
Tokamak a écrit:Sais-tu qui sont ces deux gars dans les premières vidéos ?
Au LHC ils embauchent vraiment n’importe qui.
Pas d'argument d'autorité à 2 balles, merci.
Tokamak a écrit:
En Physique cette équivalence fonctionne.
Non. Clairement pas. Sinon montrez moi où dans l'effet Casimir on a ça.
Invité- Invité
 Re: Les très grands nombres
Re: Les très grands nombres
Allez, histoire d'enfoncer le dernier clou sur cette démo foireuse :


Dernière édition par hobb le Lun 26 Mar 2018 - 21:27, édité 2 fois
Invité- Invité
Page 1 sur 2 • 1, 2 
 Sujets similaires
Sujets similaires» c'est l'histoire d'un zebre c'est pas tres long , pas tres complique, mais a peine croyable
» Je m'appelle Pollen, je suis très très sensible :) âmes sensibles: fuyez !
» Votre avis sur une situation très très délicate, svp c'est urgent !!!
» Gros son très très sale
» Une enquête très très sérieuse !
» Je m'appelle Pollen, je suis très très sensible :) âmes sensibles: fuyez !
» Votre avis sur une situation très très délicate, svp c'est urgent !!!
» Gros son très très sale
» Une enquête très très sérieuse !
Page 1 sur 2
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Évènements
Évènements