Accueil
Évènements
Rechercher
S'enregistrer
ConnexionPetit jeujeu mathématique deviendra gros casse-tête
+6
Petitagore
Pieyre
loulou38
Professeur Megamiaou
Stauk
Ardel
10 participants
Page 3 sur 6
Page 3 sur 6 • 
1, 2, 3, 4, 5, 6
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Mar 17 Mar 2015 - 9:03
Enfin bref. J'en ai fini avec les grilles censées être simples de mon échantillonnage, voici donc la première grille censée être de difficulté moyenne: la grille "mars". Je rappelle à nos chers auditeurs que le jeu consiste à cliquer de façon judicieuse sur les cases triangulaires afin de déclencher des réactions en chaîne prenant trois cases simultanément, ce qui aura pour conséquence de colorer ces cases en jaune. C'est celui d'entre vous qui trouvera le premier une façon d'atteindre le maximum possible de cases jaunes qui gagnera ce magnifique panier garni offert par notre sponsor, la charcuterie Dumoutiers du Tremblay-lès-Gonnesse, quand je pense charcutier je vais chez Dumoutiers.
Eh bien, Simone, vous qui nous parlez de Cajars, petite ville de l'Aveyron, avez-vous avec vous un sympathique candidat qui soit disposé à monter à la tribune pour nous proposer une stratégie?
Eh bien, Simone, vous qui nous parlez de Cajars, petite ville de l'Aveyron, avez-vous avec vous un sympathique candidat qui soit disposé à monter à la tribune pour nous proposer une stratégie?
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011 -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Mar 17 Mar 2015 - 11:23
Bon, visiblement, les Agnan ne se bousculent pas pour venir fayoter au tableau noir. Ce ne serait pourtant pas très difficile d'attaquer au moins la résolution du problème, il vous suffirait d'adapter un peu scolairement la méthode de "construction de cavexe" que je vous ai déjà montrée plusieurs fois au cours des récents épisodes de ce feuilleton.
Je vais émettre l'hypothèse que vous vous trouvez un peu dans l'état d'esprit où j'étais très souvent, moi, dans mes cours de maths, quand on me demandait d'appliquer mécaniquement un truc que j'étais censé savoir mais n'avais pas vraiment compris: comme je n'avais pas bien compris d'où ça venait, je voyais encore moins où ça pouvait m'emmener. Je savais certes par coeur, par exemple, que a2-b2 = (a-b) * (a+b), mais c'était du par coeur, je n'avais pas vraiment pigé que ce n'était pas "a2" mais "a au carré", et si on me mettait sous le nez un exemple pédagogique aussi scolaire que possible, je n'avais jamais l'idée de l'attaquer avec la méthode préconisée par le prof, ça me paraissait horriblement artificiel. Si on me demandait combien faisaient (3-2) * (3+2), jamais jamais jamais il ne me serait venu à l'idée de faire un truc aussi absurde que de soustraire 4 de 9 sous prétexte que 4 c'est 2 au carré et 9 c'est 3 au carré -- je trouvais vraiment que c'était chercher midi à quatorze heures et que (3 - 2) * (3 + 2), ben ça fait (1) * (5) c'est-à-dire 5, voilà. "Mais tu ne vois donc pas, bougre d'andouille, qu'il y a là une identité remarquable?" Ben non. Tout ce que je voyais, moi, c'était de la branlette intellectuelle, une volonté totalement perverse d'employer des moyens compliqués pour aboutir à des résultats simples.
Donc, plutôt que de radoter ce que je vous ai déjà dit un paquet de fois, je vais essayer de vous le présenter autrement...
Stay tuned.
Je vais émettre l'hypothèse que vous vous trouvez un peu dans l'état d'esprit où j'étais très souvent, moi, dans mes cours de maths, quand on me demandait d'appliquer mécaniquement un truc que j'étais censé savoir mais n'avais pas vraiment compris: comme je n'avais pas bien compris d'où ça venait, je voyais encore moins où ça pouvait m'emmener. Je savais certes par coeur, par exemple, que a2-b2 = (a-b) * (a+b), mais c'était du par coeur, je n'avais pas vraiment pigé que ce n'était pas "a2" mais "a au carré", et si on me mettait sous le nez un exemple pédagogique aussi scolaire que possible, je n'avais jamais l'idée de l'attaquer avec la méthode préconisée par le prof, ça me paraissait horriblement artificiel. Si on me demandait combien faisaient (3-2) * (3+2), jamais jamais jamais il ne me serait venu à l'idée de faire un truc aussi absurde que de soustraire 4 de 9 sous prétexte que 4 c'est 2 au carré et 9 c'est 3 au carré -- je trouvais vraiment que c'était chercher midi à quatorze heures et que (3 - 2) * (3 + 2), ben ça fait (1) * (5) c'est-à-dire 5, voilà. "Mais tu ne vois donc pas, bougre d'andouille, qu'il y a là une identité remarquable?" Ben non. Tout ce que je voyais, moi, c'était de la branlette intellectuelle, une volonté totalement perverse d'employer des moyens compliqués pour aboutir à des résultats simples.
Donc, plutôt que de radoter ce que je vous ai déjà dit un paquet de fois, je vais essayer de vous le présenter autrement...
Stay tuned.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Mar 17 Mar 2015 - 18:49
Mes efforts pédagogiques vont prochainement porter sur les notions de concave et convexe sur un tore. Ça me paraît, à moi qui gamberge sur ces questions depuis des années, assez simple, mais peut-être pas au point qu'il soit prudent de considérer ces notions comme comprises par le premier venu avant même de lui avoir montré un ou deux schémas explicatifs... que je n'ai pas encore publiés ici ni même concoctés. J'y travaille, je pensais en venir à bout en cinq minutes, et puis en fait je me rends compte que j'aurais avantage à fignoler. Ça va donc me prendre un certain temps, trop longtemps pour qu'il soit prudent de faire traîner le suspense quant à la résolution de la grille "mars" que j'ai soumise ce matin à votre sagacité. Donc, en deux mots et trois schémas...
Voici les cavexes que je préconise (félicitations à ceux d'entre vous qui ont compris seuls qu'il fallait se débrouiller pour terminer la résolution de cette grille sur un heptagone):
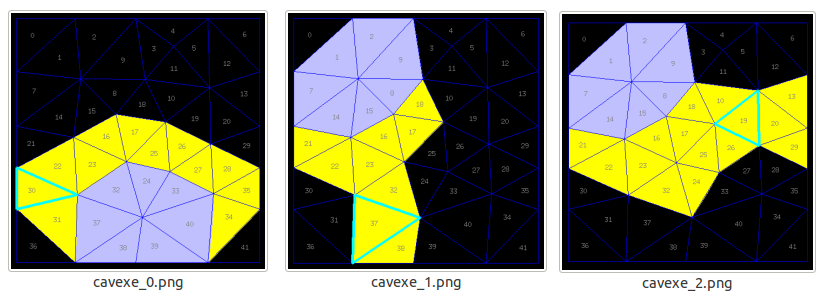
Et je vous mets en spoiler les solutions complètes élaborées à partir de ces cavexes:
A bientôt... Mais entre-temps, vos éventuelles remarques ou questions sont bienvenues.
Voici les cavexes que je préconise (félicitations à ceux d'entre vous qui ont compris seuls qu'il fallait se débrouiller pour terminer la résolution de cette grille sur un heptagone):
Et je vous mets en spoiler les solutions complètes élaborées à partir de ces cavexes:
- Solutions complètes:
- Avec le cavexe 0 (que je préconise, car c'est avec mon cerveau que j'ai trouvé cette solution): 6 10 5 20 36 2 3 21 8 (hors du cavexe), 30 35 16 26 39 (dedans).
Avec le cavexe 1 (solution informatique trouvée par mon solveur): 34 25 33 19 30 36 12 20 4 11 (hors du cavexe), 37 22 17 9 (dedans).
Avec le cavexe 2 (idem): 37 41 30 40 27 4 11 6 (hors du cavexe), 19 20 24 22 17 8 (dedans).
A bientôt... Mais entre-temps, vos éventuelles remarques ou questions sont bienvenues.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Mer 18 Mar 2015 - 10:20
Restons sur la grille "mars", mais avec l'affichage simplifié (sans numéros, et avec la seule couleur jaune pour remplir toutes les cases).
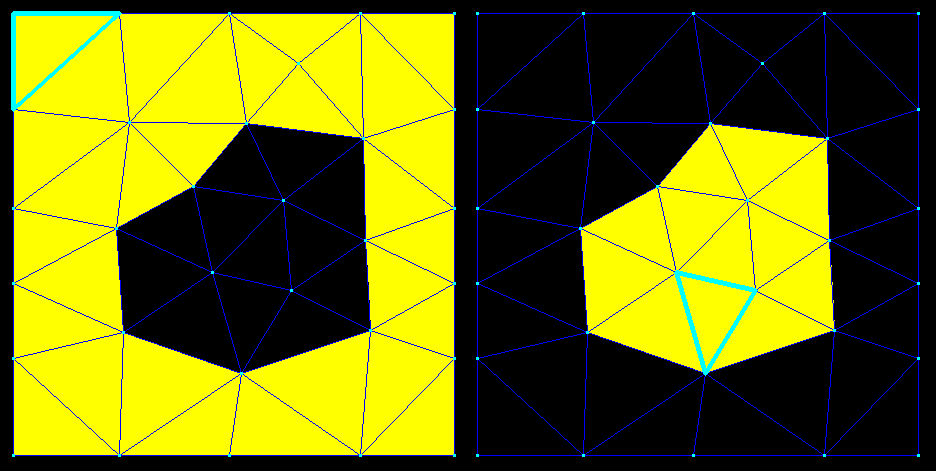
A gauche, vous voyez une situation que j'appelle concave, c'est-à-dire que la grille, déjà remplie au moins aux deux tiers, a l'air d'un morceau de gruyère jaune avec un trou (une cavité) dedans. Au contraire, à droite, la forme jaune peut être qualifiée de convexe, c'est-à-dire qu'elle ressemble à une petite patate jaune, rondouillarde, au milieu d'une grille vide.
Il est clair que l'image de gauche est le parfait inverse de l'image de droite.
Donc, merci de retenir: si ça ressemble à une petite patate, c'est convexe; si ça ressemble à un bout de gruyère avec un trou dedans, c'est concave.
Bon. Poursuivons avec un exemple à peine différent:
C'est kif-kif, l'image de gauche est toujours l'inverse parfait de l'image de droite. Maintenant, attention attention attention, je vais rajouter une case jaune à la figure de gauche, une, une seule, qui va donc pénétrer comme une pointe dans le trou noir:
Quelqu'un peut-il m'expliquer pourquoi je ne peux pas dessiner (en cliquant sur la grille) l'inverse concave exact de cette figure convexe? Essayez, vous verrez que c'est impossible.
Même topo si je rajoute une pointe à la patate de la figure de droite:
Quelqu'un peut-il m'expliquer pourquoi il est impossible, en cliquant sur la grille, de dessiner l'inverse concave de cette figure convexe?
A vrai dire, ça devrait être totalement évident pour ceux qui ont bien suivi les épisodes précédents. Mais pour ceux qui prennent le feuilleton en route -- et que je soupçonne de constituer l'essentiel de mon lectorat --, il peut être pédagogiquement intéressant de comprendre empiriquement pourquoi ces défis que je vous lance sont irréalisables.
Et bien sûr, je ne vous montre pas ça pour vous traiter de débiles mentaux, mais parce que tant qu'on n'a pas des idées parfaitement claires sur ces questions, on n'a pas la moindre chance de comprendre comment résoudre une grille, ni même en quoi consiste le défi représenté par une grille quelconque...
A gauche, vous voyez une situation que j'appelle concave, c'est-à-dire que la grille, déjà remplie au moins aux deux tiers, a l'air d'un morceau de gruyère jaune avec un trou (une cavité) dedans. Au contraire, à droite, la forme jaune peut être qualifiée de convexe, c'est-à-dire qu'elle ressemble à une petite patate jaune, rondouillarde, au milieu d'une grille vide.
Il est clair que l'image de gauche est le parfait inverse de l'image de droite.
Donc, merci de retenir: si ça ressemble à une petite patate, c'est convexe; si ça ressemble à un bout de gruyère avec un trou dedans, c'est concave.
Bon. Poursuivons avec un exemple à peine différent:
C'est kif-kif, l'image de gauche est toujours l'inverse parfait de l'image de droite. Maintenant, attention attention attention, je vais rajouter une case jaune à la figure de gauche, une, une seule, qui va donc pénétrer comme une pointe dans le trou noir:
Quelqu'un peut-il m'expliquer pourquoi je ne peux pas dessiner (en cliquant sur la grille) l'inverse concave exact de cette figure convexe? Essayez, vous verrez que c'est impossible.
Même topo si je rajoute une pointe à la patate de la figure de droite:
Quelqu'un peut-il m'expliquer pourquoi il est impossible, en cliquant sur la grille, de dessiner l'inverse concave de cette figure convexe?
A vrai dire, ça devrait être totalement évident pour ceux qui ont bien suivi les épisodes précédents. Mais pour ceux qui prennent le feuilleton en route -- et que je soupçonne de constituer l'essentiel de mon lectorat --, il peut être pédagogiquement intéressant de comprendre empiriquement pourquoi ces défis que je vous lance sont irréalisables.
Et bien sûr, je ne vous montre pas ça pour vous traiter de débiles mentaux, mais parce que tant qu'on n'a pas des idées parfaitement claires sur ces questions, on n'a pas la moindre chance de comprendre comment résoudre une grille, ni même en quoi consiste le défi représenté par une grille quelconque...
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Mer 18 Mar 2015 - 16:49
Eh bien la réponse à ces questions est tout simplement que la règle du jeu (ou les automatismes informatiques qui gèrent vos clics sur la grille "mars") imposent que dès qu'une case touche par deux de ses trois côtés deux cases déjà colorées, hop, elle devient elle-même colorée. Donc, quand on cherche à dessiner l'inverse des deux dernières images que j'ai publiées ici, la case jaune pointue qui sort de la masse jaune -- et qui touche par ses côtés deux voisins noirs -- devrait devenir une case noire qui toucherait par ses côtés deux voisins jaunes. Und das ist unmöglich: la règle imposerait qu'elle soit jaune elle-même.
Est-ce plus clair si je résume tout ça en vous disant que le tenon d'une figure convexe ne peut pas se transformer en mortaise d'une figure concave inverse?
Non, je ne suis pas sûr que ce soit plus clair. Tant pis, j'aurai quand même essayé de vous l'exprimer d'une autre façon que précédemment...
Tout ça pour vous dire que les "cavexes" que je vous conseille très vivement de dessiner avant d'attaquer la résolution d'une grille se doivent de représenter des formes aux contours "inversibles", comme sur les deux images du début du post précédent. En dessinant le cavexe, vous lui donnez une forme patatoïde qui le fait ressembler à une forme convexe -- mais quand vous résoudrez vraiment la grille, vous chercherez à redessiner cette même forme en l'entourant de cases pleines -- et ça vous donnera une figure plutôt concave.
Cela dit, et c'est pour ça que j'appelle ça un "cavexe" (ni concave ni convexe), un cavexe digne de ce nom entoure le tore et n'est donc à strictement parler ni concave ni convexe. Il est juste entre les deux, il tient le milieu entre le début de la partie (où on fait grossir une forme convexe) et la fin de la partie (où on fait se réduire le trou dans la forme concave)... donc c'est le moment psychologique fatidique dans la stratégie de résolution de la grille.
Je sais, c'est pas simple, vous avez probablement même le sentiment après avoir lu ces développements que c'est encore moins clair qu'avant. Ca ne fait rien: réfléchissez à tout ça, laissez ces idées se décanter, rêvez-en la nuit s'il le faut, vous verrez que vos petits neurones de surdoués finiront par s'orienter là-dedans.
Ou alors, c'est que c'est vraiment trop fort pour vous et que vous n'êtes même pas dignes de lire ce fil.
Est-ce plus clair si je résume tout ça en vous disant que le tenon d'une figure convexe ne peut pas se transformer en mortaise d'une figure concave inverse?
Non, je ne suis pas sûr que ce soit plus clair.
Tant pis, j'aurai quand même essayé de vous l'exprimer d'une autre façon que précédemment...Tout ça pour vous dire que les "cavexes" que je vous conseille très vivement de dessiner avant d'attaquer la résolution d'une grille se doivent de représenter des formes aux contours "inversibles", comme sur les deux images du début du post précédent. En dessinant le cavexe, vous lui donnez une forme patatoïde qui le fait ressembler à une forme convexe -- mais quand vous résoudrez vraiment la grille, vous chercherez à redessiner cette même forme en l'entourant de cases pleines -- et ça vous donnera une figure plutôt concave.
Cela dit, et c'est pour ça que j'appelle ça un "cavexe" (ni concave ni convexe), un cavexe digne de ce nom entoure le tore et n'est donc à strictement parler ni concave ni convexe. Il est juste entre les deux, il tient le milieu entre le début de la partie (où on fait grossir une forme convexe) et la fin de la partie (où on fait se réduire le trou dans la forme concave)... donc c'est le moment psychologique fatidique dans la stratégie de résolution de la grille.
Je sais, c'est pas simple, vous avez probablement même le sentiment après avoir lu ces développements que c'est encore moins clair qu'avant. Ca ne fait rien: réfléchissez à tout ça, laissez ces idées se décanter, rêvez-en la nuit s'il le faut, vous verrez que vos petits neurones de surdoués finiront par s'orienter là-dedans.
Ou alors, c'est que c'est vraiment trop fort pour vous et que vous n'êtes même pas dignes de lire ce fil.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Jeu 19 Mar 2015 - 10:07
Je vous recommande de dessiner des cavexes bien rondouillards, patatoïdes, parce qu'ainsi ces formes sont inversibles: la même séquence de coups qui vous sert à les dessiner (à partir du polygone convexe sur lequel vous pensez pouvoir terminer la résolution de la grille) pourra aussi être employée, à l'envers, quand vous voudrez résoudre intégralement la grille, depuis la grille toute vide et noire jusqu'à la grille entièrement remplie avec le maximum de cases jaunes.
Cela dit, il n'est pas dans la nature du cavexe -- défini comme la situation fatidique où la forme dessinée par les cases remplies n'est ni concave ni convexe -- d'avoir des contours rondouillards. Quand je demande à mon solveur de résoudre une grille quelconque, lui aussi, bien sûr, passe par ce moment fatidique, lui aussi dessine un cavexe. Ce dernier est assez souvent rondouillard pour que j'aie fini par en conclure qu'on pouvait faire de l'élaboration d'un cavexe rondouillard une méthode de résolution -- efficace sur la plupart des grilles. Mais dans pas mal d'autres cas, le solveur dessine des cavexes bizarroïdes, avec un ou même plusieurs triangles-tenons qui sortent de la forme concave avec des cases vides sur deux de leurs côtés. Il n'est bien sûr pas du tout interdit de résoudre une grille en employant de telles formes; simplement, je crois que c'est extrêmement difficile pour un humain de les élaborer, tandis que c'est relativement facile avec une forme rondouillarde.
Pour vous donner une idée, voici quelques cavexes biscornus dessinés par mon solveur, toujours sur la grille "mars".
A moins que vous soyez beaucoup plus imaginatifs et ingénieux que moi (ce qui n'est nullement interdit ), je ne pense pas que vous auriez pu les imaginer seuls (c'est mon solveur informatique, et non mon cerveau, qui a imaginé ces solutions). En revanche, vous devriez réussir sans grande peine à atteindre à partir de ces cavexes le score maximal de cases jaunes. Je vous invite à le faire à titre d'entraînement. Voici donc ci-dessous, en clair, six séquences de coups pour dessiner ces cavexes, suivies, en spoiler, des six solutions complètes.
Séquence de coups pour dessiner le cavexe à mortaise 0: 4 6 36 40 37 24 26 35 20 22.
Séquence de coups pour dessiner le cavexe à mortaise 1: 7 23 15 30 18 20 11 6 3 1.
Séquence de coups pour dessiner le cavexe à mortaise 2: 0 38 41 40 32 25 5 10.
Séquence de coups pour dessiner le cavexe à mortaise 3: 36 11 6 13 2 19 21 30 35.
Séquence de coups pour dessiner le cavexe à mortaise 4: 2 36 7 34 5 30 21 29 8.
Séquence de coups pour dessiner le cavexe à mortaise 5: 12 21 7 0 31 23 8 3.
Cela dit, il n'est pas dans la nature du cavexe -- défini comme la situation fatidique où la forme dessinée par les cases remplies n'est ni concave ni convexe -- d'avoir des contours rondouillards. Quand je demande à mon solveur de résoudre une grille quelconque, lui aussi, bien sûr, passe par ce moment fatidique, lui aussi dessine un cavexe. Ce dernier est assez souvent rondouillard pour que j'aie fini par en conclure qu'on pouvait faire de l'élaboration d'un cavexe rondouillard une méthode de résolution -- efficace sur la plupart des grilles. Mais dans pas mal d'autres cas, le solveur dessine des cavexes bizarroïdes, avec un ou même plusieurs triangles-tenons qui sortent de la forme concave avec des cases vides sur deux de leurs côtés. Il n'est bien sûr pas du tout interdit de résoudre une grille en employant de telles formes; simplement, je crois que c'est extrêmement difficile pour un humain de les élaborer, tandis que c'est relativement facile avec une forme rondouillarde.
Pour vous donner une idée, voici quelques cavexes biscornus dessinés par mon solveur, toujours sur la grille "mars".
A moins que vous soyez beaucoup plus imaginatifs et ingénieux que moi (ce qui n'est nullement interdit
), je ne pense pas que vous auriez pu les imaginer seuls (c'est mon solveur informatique, et non mon cerveau, qui a imaginé ces solutions). En revanche, vous devriez réussir sans grande peine à atteindre à partir de ces cavexes le score maximal de cases jaunes. Je vous invite à le faire à titre d'entraînement. Voici donc ci-dessous, en clair, six séquences de coups pour dessiner ces cavexes, suivies, en spoiler, des six solutions complètes.Séquence de coups pour dessiner le cavexe à mortaise 0: 4 6 36 40 37 24 26 35 20 22.
- solution complète:
- 4 6 36 40 37 24 26 35 20 22 (hors du cavexe), 12 11 17 8 (dedans).
Séquence de coups pour dessiner le cavexe à mortaise 1: 7 23 15 30 18 20 11 6 3 1.
- solution complète:
- 7 23 15 30 18 20 11 6 3 1 (hors du cavexe), 36 35 26 24 (dedans).
Séquence de coups pour dessiner le cavexe à mortaise 2: 0 38 41 40 32 25 5 10.
- solution complète:
- 0 38 41 40 32 25 5 10 (hors du cavexe), 26 35 20 22 17 8 (dedans).
Séquence de coups pour dessiner le cavexe à mortaise 3: 36 11 6 13 2 19 21 30 35.
- solution complète:
- 36 11 6 13 2 19 21 30 35 (hors du cavexe), 3 8 16 26 24 (dedans).
Séquence de coups pour dessiner le cavexe à mortaise 4: 2 36 7 34 5 30 21 29 8.
- solution complète:
- 2 36 7 34 5 30 21 29 8 (hors du cavexe), 3 10 16 26 24 (dedans).
Séquence de coups pour dessiner le cavexe à mortaise 5: 12 21 7 0 31 23 8 3.
- solution complète:
- 12 21 7 0 31 23 8 3 (hors du cavexe), 5 18 20 35 26 33 (dedans).
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Ven 20 Mar 2015 - 9:20
Il m'est arrivé hier un incident sans importance qui m'a quand même passablement préoccupé. J'étais dans un restaurant pas très fréquenté avec un ami, et nous discutions sur le ton normal de deux personnes qui discutent à table: pas fort, mais pas en chuchotant -- et comme lui comme moi sommes capables de nous intéresser à ce que nous disons, nous avions une conversation animée. Sans nous en rendre compte, nous avons importuné des gens qui déjeunaient à une table voisine -- probablement, entre autres, en exprimant de façon un peu virulente le peu d'estime que nous inspirent certaines opinions politiques qui devaient être celles de ces braves gens. Mais il se trouve qu'au moment où nos voisins exaspérés nous ont plus ou moins intimé l'ordre de nous taire ou de foutre le camp (à leur décharge, ils avaient visiblement attendu que nous ayons fini notre café, et ont explosé en constatant que nous avions l'intention de continuer à discuter après avoir terminé le repas), le sujet dont nous discutions ne me paraissait pas prêter à polémique -- vu qu'il s'agissait, précisément, de mon jeujeu de triangles (je suis un peu monomaniaque, peut-être l'avez-vous déjà noté).
Je comprends très bien que la plupart des gens n'en aient rien à cirer des réactions en chaîne dans un réseau de triangles torique. Je comprends même, quoique ça ait tendance à me désoler, que certains, comme vous, hypocrites lecteurs mes semblables mes frères, me lisent sans jamais réagir à ce que je dis. Mais c'est la première fois que j'ai eu le sentiment de me faire détester parce que je m'intéresse à des trucs prise de tête au lieu de ne tout simplement pas moufter comme le pékin lambda...
Ah la la, le zèbre, cet inadapté social, la haine de l'intelligence, et toutes ces sortes de choses.
Du coup, me sentant assez déconcerté, j'ai besoin de reprendre mes esprits, et donc je reprends le fil de ma passionnante saga là où je l'avais laissé, de façon totalement scolaire. La grille du jour sera la grille "avril", une belle grille composée de cinq rangées horizontales disposées presque comme à la parade.
Un volontaire pour me dessiner un cavexe, ou au moins me choisir un polygone final?
Ou juste pour dire un petit mot en passant pour que je me sente moins seul et mal-aimé?
Je comprends très bien que la plupart des gens n'en aient rien à cirer des réactions en chaîne dans un réseau de triangles torique. Je comprends même, quoique ça ait tendance à me désoler, que certains, comme vous, hypocrites lecteurs mes semblables mes frères, me lisent sans jamais réagir à ce que je dis. Mais c'est la première fois que j'ai eu le sentiment de me faire détester parce que je m'intéresse à des trucs prise de tête au lieu de ne tout simplement pas moufter comme le pékin lambda...
Ah la la, le zèbre, cet inadapté social, la haine de l'intelligence, et toutes ces sortes de choses.
Du coup, me sentant assez déconcerté, j'ai besoin de reprendre mes esprits, et donc je reprends le fil de ma passionnante saga là où je l'avais laissé, de façon totalement scolaire. La grille du jour sera la grille "avril", une belle grille composée de cinq rangées horizontales disposées presque comme à la parade.
Un volontaire pour me dessiner un cavexe, ou au moins me choisir un polygone final?
Ou juste pour dire un petit mot en passant pour que je me sente moins seul et mal-aimé?
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Ven 20 Mar 2015 - 11:43
On nous écrit de Carpentras:
Ah boooon?
En effet, cette réponse m'aurait comblé d'aise... La grille "avril" ayant 36 cases, et vu qu'il faut presque toujours sacrifier deux cases au départ...
C'est cela.
Cela paraît concevable, mon petit, mais cela ne te dispenserait point de dessiner un cavexe.
Tu es révolté mais ton coeur est pur et ton esprit vif, mon enfant. Sauras-tu pousser ta réflexion jusqu'à la résolution complète de la grille?
Je ne t'en ferai pas le reproche.
Ptikon, va.
Jean-Pierre Liégeois, lecteur de Carpentras a écrit:Cher maître, je ne voudrais pas vous paraître narquois, mais je pense qu'il y a une faille dans votre enseignement.
Ah boooon?
Jean-Pierre Liégeois a écrit:Parce que ce que vous vous attendez à ce qu'on vous dise, sur votre grille "avril" à la noix, là, c'est qu'il faut terminer sur un heptagone marié à un pentagone, pas vrai?
En effet, cette réponse m'aurait comblé d'aise... La grille "avril" ayant 36 cases, et vu qu'il faut presque toujours sacrifier deux cases au départ...
Jean-Pierre Liégeois a écrit:... il restera 34 cases, et 34 étant égal à un multiple de 3 majoré de 1, il va falloir terminer sur un multiple de 3 majoré de 1 -- qui ne peut guère être qu'un heptagone.
C'est cela.
Jean-Pierre Liégeois a écrit:Seulement, je vous le demande, cher maître, qu'est-ce qui m'empêche, au lieu de sacrifier deux cases au début pour terminer sur un heptagone, d'en sacrifier plutôt trois pour terminer sur un hexagone?
Je sais bien que l'arithmétique n'est pas votre fort, mais enfin, 2 + 7, chez moi, c'est égal à 3 + 6, donc j'aboutirais au même optimum de cases jaunes, à savoir 36 cases dans la grille, moins 9 = 27 = 3 x 9, neuf coups gagnants colorant 27 cases en jaune. Non?
Cela paraît concevable, mon petit, mais cela ne te dispenserait point de dessiner un cavexe.
Jean-Pierre Liégeois a écrit:No problemo, baby. Je choisis pour hexagone final les cases 4, 5, 6, 33, 34, 35. Je jouerai l'avant-dernier coup dans le pentagone marié à cet hexagone en prenant, en jaune, les cases 3, 31 et 32, et les cases 29, 22 et 30 achèveront de constituer un excellent cavexe... avec dedans un hexagone bleu au lieu d'un heptagone.
Tu es révolté mais ton coeur est pur et ton esprit vif, mon enfant. Sauras-tu pousser ta réflexion jusqu'à la résolution complète de la grille?
Jean-Pierre Liégeois a écrit:Mais on est bien d'accord, en sacrifiant trois cases au début?
Je ne t'en ferai pas le reproche.
Jean-Pierre Liégeois a écrit:Alors numérote tes abattis, pépé, la voici ma solution et je t'assure qu'elle décoiffe: 7 0 11 (trois cases sacrifiées), 2 8 20 17 15 27 24 (hors du cavexe), 22 31 34 (dedans). Et j'ai bien joué neuf coups gagnants, donc j'ai bel et bien atteint l'optimum, nananère.
Alors, vieux, on fait moins le malin, hein?
Ptikon, va.
Dernière édition par Petitagore le Ven 20 Mar 2015 - 11:50, édité 1 fois (Raison : un mot pour un autre)
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Ven 20 Mar 2015 - 16:28
Eh bien oui, Jean-Pierre Liégeois a raison, on peut atteindre le même optimum (ou maximum) de cases jaunes en sacrifiant trois cases au départ pour terminer sur un hexagone, plutôt qu'en sacrifiant deux cases au départ pour terminer sur un heptagone. Cela étant, ça n'est généralement pas plus simple, et personnellement je trouve ça moins élégant -- je serais bien en peine d'expliquer pourquoi -- de sorte que je ne recherche pas de telles solutions avant d'avoir perdu tout espoir d'en trouver de plus classiques.
Quand deux solutions permettent d'aboutir au même optimum, pourquoi soutenir que certaines sont plus esthétiques, plus élégantes, que d'autres? Je ne sais pas, mais intuitivement, par exemple, j'aurais tendance à soutenir que pour résoudre la grille "avril" qui nous occupe depuis ce matin, il y a bien des solutions plus élégantes que d'autres -- et qui ne ressemblent pas à celles de Jean-Pierre Liégeois. Je m'empresse d'ajouter que je trouve ces solutions plus esthétiques alors que je n'en ai pas eu l'idée moi-même, et qu'une fois de plus c'est mon fichu solveur qui m'a signalé leur possibilité.
Sur la grille "avril", il faudrait classiquement sacrifier deux cases au départ et terminer sur un ensemble de sept cases. Eh bien, si vous regardez bien, vous vous rendrez compte que cet ensemble de sept cases n'est pas nécessairement un heptagone, que ce pourrait aussi être un couloir de sept cases: par exemple, les cases 8, 9, 10, 11, 12, 16, 13, ou 17, 14, 18, 15, 19, 20, 21. Ce n'est pas forcément plus facile qu'avec un cavexe rondouillard... mais je trouve ça plus satisfaisant pour l'esprit, allez savoir pourquoi.
Il est rare que les couloirs de cases qui traversent une grille Triancey comportent moins de huit cellules (raison pour laquelle je n'avais pas songé à cette possibilité). C'est peut-être pour cela que j'aime mieux ces solutions: elles tirent parti d'une circonstance rare. Mais elles mènent au même score.
Je ne vous indique pas ces solutions tout de suite: les savoir possibles vous incitera peut-être à vous creuser la tête pour les trouver (or faire carburer votre cerveau à vous est ma seule ambition, légèrement sadique sans doute, mais c'est pour la bonne cause).
Quand deux solutions permettent d'aboutir au même optimum, pourquoi soutenir que certaines sont plus esthétiques, plus élégantes, que d'autres? Je ne sais pas, mais intuitivement, par exemple, j'aurais tendance à soutenir que pour résoudre la grille "avril" qui nous occupe depuis ce matin, il y a bien des solutions plus élégantes que d'autres -- et qui ne ressemblent pas à celles de Jean-Pierre Liégeois. Je m'empresse d'ajouter que je trouve ces solutions plus esthétiques alors que je n'en ai pas eu l'idée moi-même, et qu'une fois de plus c'est mon fichu solveur qui m'a signalé leur possibilité.
Sur la grille "avril", il faudrait classiquement sacrifier deux cases au départ et terminer sur un ensemble de sept cases. Eh bien, si vous regardez bien, vous vous rendrez compte que cet ensemble de sept cases n'est pas nécessairement un heptagone, que ce pourrait aussi être un couloir de sept cases: par exemple, les cases 8, 9, 10, 11, 12, 16, 13, ou 17, 14, 18, 15, 19, 20, 21. Ce n'est pas forcément plus facile qu'avec un cavexe rondouillard... mais je trouve ça plus satisfaisant pour l'esprit, allez savoir pourquoi.
Il est rare que les couloirs de cases qui traversent une grille Triancey comportent moins de huit cellules (raison pour laquelle je n'avais pas songé à cette possibilité). C'est peut-être pour cela que j'aime mieux ces solutions: elles tirent parti d'une circonstance rare. Mais elles mènent au même score.
Je ne vous indique pas ces solutions tout de suite: les savoir possibles vous incitera peut-être à vous creuser la tête pour les trouver (or faire carburer votre cerveau à vous est ma seule ambition, légèrement sadique sans doute, mais c'est pour la bonne cause).
Dernière édition par Petitagore le Ven 20 Mar 2015 - 16:30, édité 1 fois (Raison : faute de frappe)
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Ven 20 Mar 2015 - 18:26
Bon, je vais quand même donner la vedette au cavexe sorti de mon cerveau, même si je ne trouve pas qu'il constitue la solution la plus élégante:
Et voici six autres cavexes trouvés, cette fois, par les automatismes informatiques de mon solveur. Je préfère les deux premiers, qui prennent des couloirs de sept cases, ce sont à mon sens les plus élégants. Mais les deux suivants sont quand même remarquablement concis, et c'est ce genre de formes que l'esprit d'un joueur humain doit se glorifier de réussir à identifier (comme vous le voyez, aujourd'hui je n'y suis pas parvenu: faites ce que je dis, ne faites pas ce que je fais!).
En revanche, le dernier cavexe, très massif, n'aurait pas retenu mon attention: sauf exceptions, je pense qu'il est préférable de s'astreindre à mettre sensiblement moins de la moitié des cases dans le cavexe. Mais ça n'empêche pas qu'on peut atteindre l'optimum de cases jaunes sur la base de ce cavexe comme sur sur celle des autres.
Et voici les solutions complètes, sous spoiler comme d'habitude:
Peut-être pas à demain, car je dois prendre un train relativement tôt... A dimanche, plutôt.
Et voici six autres cavexes trouvés, cette fois, par les automatismes informatiques de mon solveur. Je préfère les deux premiers, qui prennent des couloirs de sept cases, ce sont à mon sens les plus élégants. Mais les deux suivants sont quand même remarquablement concis, et c'est ce genre de formes que l'esprit d'un joueur humain doit se glorifier de réussir à identifier (comme vous le voyez, aujourd'hui je n'y suis pas parvenu: faites ce que je dis, ne faites pas ce que je fais!).
En revanche, le dernier cavexe, très massif, n'aurait pas retenu mon attention: sauf exceptions, je pense qu'il est préférable de s'astreindre à mettre sensiblement moins de la moitié des cases dans le cavexe. Mais ça n'empêche pas qu'on peut atteindre l'optimum de cases jaunes sur la base de ce cavexe comme sur sur celle des autres.
Et voici les solutions complètes, sous spoiler comme d'habitude:
- Solutions complètes:
- Avec le cavexe humain sorti de mon cerveau malade: 17 2 9 0 6 20 29 (hors du cavexe), 12 15 27 4 25 (dedans).
Avec le cavexe 0 (couloir): 7 30 2 4 35 33 26 22 20 24 15 (hors du cavexe), 8 (dedans).
Avec le cavexe 1 (couloir): 23 31 25 1 10 5 7 13 12 34 27 (hors du cavexe), 14 (dedans).
Avec le cavexe 2 (remarquablement concis): 11 0 2 14 6 12 21 15 27 (hors du cavexe), 34 33 25 (dedans).
Avec le cavexe 3 (remarquablement concis): 18 29 23 9 27 32 33 15 13 (hors du cavexe), 7 30 2 (dedans).
Avec le cavexe 4: 4 7 8 35 27 20 29 (hors du cavexe), 10 26 14 3 32 (dedans).
Avec le cavexe 5 (horriblement massif):
0 18 9 23 30 28 (hors du cavexe), 26 20 16 35 31 11 (dedans).
Peut-être pas à demain, car je dois prendre un train relativement tôt... A dimanche, plutôt.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Dim 22 Mar 2015 - 10:03
Le problème du jour est la résolution de la grille "juin":
J'ai perdu l'espoir de vous faire réagir, chers lecteurs, -- et pourtant, le compteur de Zebras Crossing indique que vous n'êtes pas inexistants --, donc je vais monologuer sans scrupules.
Ca ne saute pas aux yeux, mais cette grille n'est pas tout à fait banale en ce sens que la densité des cases, au lieu d'être uniforme comme presque toujours, est nettement plus élevée dans le coin supérieur gauche que dans son opposé. Mais ça ne change rigoureusement rien aux principes de résolution.
Il y a quarante cases. Si, fort classiquement, on en sacrifie deux pour initier les coups gagnants (qui prennent les cases trois par trois et les colorent en jaune), il en restera donc trente-huit, qui est un multiple de trois minoré de un. Ergo, il faut terminer sur un polygone convexe dont le nombre de cases soit lui-même un multiple de trois minoré de un, par exemple un pentagone. L'avant-dernier coup d'une partie à score optimal "classique" étant toujours joué, lui aussi, sur un pentagone, nous sommes donc à la recherche d'un couple de pentagones (ayant deux cases en commun comme à peu près tous les polygones convexes mariés de toutes les grilles).
Un couple de ce type n'existe qu'en un seul endroit de la figure. Je ne vous dirai pas tout de suite où, parce que si vous ne le cherchez pas vous-mêmes vous n'acquerrez jamais l'entraînement nécessaire pour devenir champions de mon casse--tête... donc, cherchez bien.
Saurez-vous dessiner un cavexe sur la base de ce couple de pentagones? A vrai dire, ce n'est pas bien malin, mais la première idée qui vous viendra ne sera pas nécessairement la bonne -- c'est-à-dire celle qui pourrait vous permettre de remplir la grille avec le maximum de cases jaunes (33, correspondant à 11 coups gagnants).
J'ai perdu l'espoir de vous faire réagir, chers lecteurs, -- et pourtant, le compteur de Zebras Crossing indique que vous n'êtes pas inexistants --, donc je vais monologuer sans scrupules.
Ca ne saute pas aux yeux, mais cette grille n'est pas tout à fait banale en ce sens que la densité des cases, au lieu d'être uniforme comme presque toujours, est nettement plus élevée dans le coin supérieur gauche que dans son opposé. Mais ça ne change rigoureusement rien aux principes de résolution.
Il y a quarante cases. Si, fort classiquement, on en sacrifie deux pour initier les coups gagnants (qui prennent les cases trois par trois et les colorent en jaune), il en restera donc trente-huit, qui est un multiple de trois minoré de un. Ergo, il faut terminer sur un polygone convexe dont le nombre de cases soit lui-même un multiple de trois minoré de un, par exemple un pentagone. L'avant-dernier coup d'une partie à score optimal "classique" étant toujours joué, lui aussi, sur un pentagone, nous sommes donc à la recherche d'un couple de pentagones (ayant deux cases en commun comme à peu près tous les polygones convexes mariés de toutes les grilles).
Un couple de ce type n'existe qu'en un seul endroit de la figure. Je ne vous dirai pas tout de suite où, parce que si vous ne le cherchez pas vous-mêmes vous n'acquerrez jamais l'entraînement nécessaire pour devenir champions de mon casse--tête... donc, cherchez bien.
- oùkilèti le couple de pentagones?:
- Le pentagone 2, 3, 4, 11, 12 est marié par les cases 3 et 4 au pentagone 3, 4, 5, 37, 38. Ah ben ouais, ce dernier est coupé en deux morceaux, mais je vous rappelle que les cases du haut sont censées toucher celles du bas vu que nos grilles de triangles sont toutes des tores.
Saurez-vous dessiner un cavexe sur la base de ce couple de pentagones? A vrai dire, ce n'est pas bien malin, mais la première idée qui vous viendra ne sera pas nécessairement la bonne -- c'est-à-dire celle qui pourrait vous permettre de remplir la grille avec le maximum de cases jaunes (33, correspondant à 11 coups gagnants).
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Dim 22 Mar 2015 - 18:17
Avant d'indiquer les solutions complètes, je vais profiter d'une spécificité de la grille "juin" que nous étudions pour poser une question dont la réponse est moins évidente qu'il y paraît: est-il correct de dire que le cavexe le plus concis est toujours le meilleur? Par "concis", j'entends évidemment "composé d'un nombre de cases réduit".
Et pour orienter la réponse, je publie tout de suite un échantillonnage assez complet des cavexes utilisables sur cette grille:
Ce ne sont pas neuf cavexes en vrac, mais 3 groupes horizontaux de 3 cavexes constituant clairement des variantes d'une même idée. Il est clair que si vous trouvez un moyen d'entourer le cavexe 0c, vous pouvez continuer sur 0a comme sur 0b. Même remarque pour la deuxième rangée: si vous trouvez un moyen d'entourer le cavexe 1c, il est clair que vous pouvez continuer sur 1a ou 1b, à votre choix.
La troisième rangée est un peu différente: si vous parvenez à entamer la grille sans toucher au cavexe 2c, vous avez accès au cavexe 2b, et en aval de lui au cavexe 2a. Cela étant, le cavexe 2c est tellement massif qu'en première analyse on pourrait être tenté d'affirmer que le 0a est de loin préférable (il laisse une bien plus grande liberté d'action pour déterminer les premiers coups, ceux qui ne touchent pas le cavexe).
Sauf que c'est précisément la pauvreté des choix pour jouer les premiers coups sans toucher au cavexe 2c qui rend ce cavexe intéressant: il y a tellement peu de choix que la solution complète tombe sous le sens.
Cela fait partie des réflexions philosophiques auxquelles mon jeujeu peut donner accès: la grande liberté vous laisse l'embarras du choix, la contrainte vous mène parfois directement à une solution complète.
De là à en conclure que le totalitarisme simplifie la vie des gens tandis que la société prétendument libérale les amène à se désespérer face à la multitude des choix possibles, il y a un pas... que personnellement je vous incite vivement à ne pas franchir! Mais on peut y réfléchir quand même...
Vous noterez au passage que les séquences finales de toutes ces solutions se ressemblent furieusement, car en effet il n'y a guère de choix pour enchaîner les groupes de trois cases à proximité immédiate du couple de pentagones. Là encore, il est manifeste que l'absence de choix simplifie la réflexion.
Et pour orienter la réponse, je publie tout de suite un échantillonnage assez complet des cavexes utilisables sur cette grille:
Ce ne sont pas neuf cavexes en vrac, mais 3 groupes horizontaux de 3 cavexes constituant clairement des variantes d'une même idée. Il est clair que si vous trouvez un moyen d'entourer le cavexe 0c, vous pouvez continuer sur 0a comme sur 0b. Même remarque pour la deuxième rangée: si vous trouvez un moyen d'entourer le cavexe 1c, il est clair que vous pouvez continuer sur 1a ou 1b, à votre choix.
La troisième rangée est un peu différente: si vous parvenez à entamer la grille sans toucher au cavexe 2c, vous avez accès au cavexe 2b, et en aval de lui au cavexe 2a. Cela étant, le cavexe 2c est tellement massif qu'en première analyse on pourrait être tenté d'affirmer que le 0a est de loin préférable (il laisse une bien plus grande liberté d'action pour déterminer les premiers coups, ceux qui ne touchent pas le cavexe).
Sauf que c'est précisément la pauvreté des choix pour jouer les premiers coups sans toucher au cavexe 2c qui rend ce cavexe intéressant: il y a tellement peu de choix que la solution complète tombe sous le sens.
Cela fait partie des réflexions philosophiques auxquelles mon jeujeu peut donner accès: la grande liberté vous laisse l'embarras du choix, la contrainte vous mène parfois directement à une solution complète.
De là à en conclure que le totalitarisme simplifie la vie des gens tandis que la société prétendument libérale les amène à se désespérer face à la multitude des choix possibles, il y a un pas... que personnellement je vous incite vivement à ne pas franchir!
Mais on peut y réfléchir quand même...- Solutions complètes:
- Solution avec le cavexe 0a (élaboré par le cerveau humain de votre serviteur; toutes les autres solutions ont été trouvées par un solveur informatique): 33 36 35 28 24 9 18 0 16 (hors du cavexe), 32 20 14 38 12 (dedans).
Solution avec les cavexes 0b et 0c: 30 1 39 16 18 22 23 35 (hors du cavexe), 32 33 20 14 38 12 (dedans).
Solution avec le cavexe 1a: 8 22 24 29 1 19 32 30 (hors du cavexe), 27 39 16 13 5 2 (dedans).
Solution avec les cavexes 1b et 1c: 19 31 26 10 17 36 0 (hors du cavexe), 27 28 35 16 14 38 4 (dedans).
Solution avec les cavexes 2a, 2b et 2c (massifs à l'extrême): 7 28 15 35 (hors du cavexe), 33 24 26 36 0 18 21 6 38 4 (dedans).
Je ne sais pas si vous en tomberez d'accord, mais pour moi c'est nettement cette dernière solution qui donne le plus le sentiment de l'élégance.
Vous noterez au passage que les séquences finales de toutes ces solutions se ressemblent furieusement, car en effet il n'y a guère de choix pour enchaîner les groupes de trois cases à proximité immédiate du couple de pentagones. Là encore, il est manifeste que l'absence de choix simplifie la réflexion.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Lun 23 Mar 2015 - 8:41
Le problème du jour sera la résolution de la grille "aout".
Voilà une grille qui m'a donné une grande satisfaction intellectuelle: un problème simple, propre, sans chichis, avec un cavexe facile à dessiner, facile à photographier mentalement, suivi d'une méthode de résolution logique, académique et sans bavures. Veni, vidi, vici, je suis devenu un vrai pro de mon jeujeu.
Comme de coutume, je reviendrai dans la journée pour orienter vos réflexions.
Voilà une grille qui m'a donné une grande satisfaction intellectuelle: un problème simple, propre, sans chichis, avec un cavexe facile à dessiner, facile à photographier mentalement, suivi d'une méthode de résolution logique, académique et sans bavures. Veni, vidi, vici, je suis devenu un vrai pro de mon jeujeu.
Comme de coutume, je reviendrai dans la journée pour orienter vos réflexions.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Lun 23 Mar 2015 - 17:15
Bon, eh bien si vous n'avez pas compris seuls que pour résoudre la grille "aout", il fallait rechercher dessus un heptagone marié à un pentagone, ben c'est à désespérer des vertus pédagogiques de la répétition...
Nous avons une grille de 42 cases. J'en sacrifie deux (bleues) au départ pour initier la série de coups gagnants (jaunes) prenant les cases trois par trois... Il me reste donc 42 - 2 = 40 cases. Quarante est un multiple de trois majoré de un, il me faut donc terminer sur un polygone convexe dont le nombre de cases soit lui-même un multiple de trois majoré de un, donc un heptagone. Et comme l'avant-dernier coup d'une partie à score optimal "classique" est toujours joué sur un pentagone marié par deux cases au polygone final, nous cherchons des couples heptagone-pentagone.
Bon, ben c'est pas ça qui manque, et la plupart sont en plus utilisables pour dessiner des cavexes. Et je le prouve:
C'est pas l'embarras du choix, ça? Vous pouvez employer en haut à gauche l'heptagone 0, 1, 2, 3, 6, 7, 8 (marié au pentagone 2, 3, 4, 37, 38) pour dessiner un cavexe horizontal (le cavexe 0 ci-dessus) ou vertical (le cavexe 1). Vous pouvez employer en haut à droite l'heptagone 9, 10, 11, 16, 17, 18, 19 (marié au pentagone 12, 13, 18, 19, 25) pour dessiner un cavexe horizontal (le cavexe 2) ou vertical (le cavexe 3). Vous pouvez employer l'heptagone 12, 6, 7, 13, 20, 21, 14 (marié au pentagone 12, 13, 18, 19, 25) pour dessiner un cavexe horizontal d'une remarquable concision (le cavexe 4). Vous pouvez employer l'heptagone 28, 29, 30, 36, 37, 38, 39 (marié au pentagone 22, 23, 29, 30, 31) pour dessiner un beau cavexe vertical entouré de deux colonnes de cases vides de part et d'autre de la grille (le cavexe 5, qui lui-même peut être affiné de deux façons différentes). Et vous pouvez enfin employer l'heptagone 30, 31, 24, 32, 39, 40, 41 pour dessiner un cavexe horizontal (le cavexe 6, qui profite du mariage avec le pentagone 26, 27, 33, 32, 41) ou un cavexe vertical (le cavexe 7, qui profite du mariage avec un deuxième pentagone, 22, 23, 29, 30, 31). N'en jetez plus, la cour est pleine...
Je reviendrai plus tard pour les solutions complètes. A votre place, je commencerais par le cavexe 5, qui est le plus facile à photographier mentalement, coincé qu'il est entre deux colonnes de cases -- mais pour être honnête, la solution que moi j'ai trouvée (les autres ont été imaginées par mon solveur... et parfois un peu améliorées ensuite par moi pour les rendre plus élégantes), c'est celle qui employait le cavexe 7.
Nous avons une grille de 42 cases. J'en sacrifie deux (bleues) au départ pour initier la série de coups gagnants (jaunes) prenant les cases trois par trois... Il me reste donc 42 - 2 = 40 cases. Quarante est un multiple de trois majoré de un, il me faut donc terminer sur un polygone convexe dont le nombre de cases soit lui-même un multiple de trois majoré de un, donc un heptagone. Et comme l'avant-dernier coup d'une partie à score optimal "classique" est toujours joué sur un pentagone marié par deux cases au polygone final, nous cherchons des couples heptagone-pentagone.
Bon, ben c'est pas ça qui manque, et la plupart sont en plus utilisables pour dessiner des cavexes. Et je le prouve:
C'est pas l'embarras du choix, ça? Vous pouvez employer en haut à gauche l'heptagone 0, 1, 2, 3, 6, 7, 8 (marié au pentagone 2, 3, 4, 37, 38) pour dessiner un cavexe horizontal (le cavexe 0 ci-dessus) ou vertical (le cavexe 1). Vous pouvez employer en haut à droite l'heptagone 9, 10, 11, 16, 17, 18, 19 (marié au pentagone 12, 13, 18, 19, 25) pour dessiner un cavexe horizontal (le cavexe 2) ou vertical (le cavexe 3). Vous pouvez employer l'heptagone 12, 6, 7, 13, 20, 21, 14 (marié au pentagone 12, 13, 18, 19, 25) pour dessiner un cavexe horizontal d'une remarquable concision (le cavexe 4). Vous pouvez employer l'heptagone 28, 29, 30, 36, 37, 38, 39 (marié au pentagone 22, 23, 29, 30, 31) pour dessiner un beau cavexe vertical entouré de deux colonnes de cases vides de part et d'autre de la grille (le cavexe 5, qui lui-même peut être affiné de deux façons différentes). Et vous pouvez enfin employer l'heptagone 30, 31, 24, 32, 39, 40, 41 pour dessiner un cavexe horizontal (le cavexe 6, qui profite du mariage avec le pentagone 26, 27, 33, 32, 41) ou un cavexe vertical (le cavexe 7, qui profite du mariage avec un deuxième pentagone, 22, 23, 29, 30, 31). N'en jetez plus, la cour est pleine...
Je reviendrai plus tard pour les solutions complètes. A votre place, je commencerais par le cavexe 5, qui est le plus facile à photographier mentalement, coincé qu'il est entre deux colonnes de cases -- mais pour être honnête, la solution que moi j'ai trouvée (les autres ont été imaginées par mon solveur... et parfois un peu améliorées ensuite par moi pour les rendre plus élégantes), c'est celle qui employait le cavexe 7.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Lun 23 Mar 2015 - 18:19
Allez, sans plus attendre (il faut que je sorte faire des courses), voici les solutions complètes pour la grille "aout" (sous spoiler, bien entendu):
- Solutions complètes:
- Avec le cavexe 0: 31 23 29 16 25 12 10 26 28 35 (hors du cavexe), 41 39 37 8 (dedans).
Avec le cavexe 1: 40 22 30 24 18 12 9 5 33 20 (hors du cavexe), 14 34 4 0 (dedans).
Avec le cavexe 2: 0 3 34 27 40 28 38 31 32 15 21 (hors du cavexe), 7 13 17 (dedans).
Avec le cavexe 3: 27 26 41 1 37 21 5 7 22 (hors du cavexe), 38 23 12 3 17 (dedans).
Avec le cavexe 4: 1 4 8 11 40 33 37 27 29 23 32 (hors du cavexe), 17 18 12 (dedans). Variante: 35 29 37 39 23 33 5 32 1 8 10 (hors du cavexe), 16 18 7 (dedans).
Avec le cavexe 5: 35 11 33 0 12 20 40 18 (hors du cavexe), 23 15 7 9 2 30 (dedans).
Avec le cavexe 6: 17 4 9 2 36 34 5 22 6 19 (hors du cavexe), 28 13 27 30 (dedans).
Avec le cavexe 7: 34 12 0 27 20 28 3 7 16 4 (hors du cavexe), 11 18 22 31 (dedans).
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Mar 24 Mar 2015 - 8:58
Le problème du jour sera la résolution de la grille "novembre".
Comme ça, à vue de nez, j'aurais tendance à dire qu'elle va être du même genre que la grille d'hier (elle a en tout cas le même nombre de cases, donc il faut la terminer de la même façon, sur un heptagone marié à un pentagone) -- et en la résolvant à l'instant, je l'ai trouvée plutôt facile. Question d'entraînement... A défaut d'autre chose, la rédaction de ce fil de discussion m'entraîne et même me mène à une certaine virtuosité -- qui n'impressionne personne, mais dont je suis quand même plutôt content.
Je suppose que vous l'aurez compris, les notules que je publie ici sont vouées à être reprises dans un petit ouvrage que je publierai sur Internet (sous une licence de libre diffusion, bien entendu -- la CC-BY, pour ceux qui connaissent les licences Creative Commons)... et Dieu sait ce que ça deviendra, mais j'ai quand même la certitude mathématique qu'il y aura encore dans mes grilles de quoi réjouir l'esprit de bargeots dans mon genre dans trois mille ans -- si l'humanité existe encore d'une part, si j'ai réussi à intéresser assez de monde à mes gamberges pour que le souvenir n'en disparaisse pas totalement, d'autre part. M'astreindre à alimenter ce fil tous les jours m'oblige à chercher plein d'exemples pédagogiques, à les creuser à fond et à travailler à leur lisibilité, tout en m'assurant que les solutions peuvent bel et bien être élaborées par des humains et non pas seulement des automatismes informatiques.
Aujourd'hui, il me paraît flagrant que la grille est très facile à résoudre de façon méthodique -- mais encore faut-il avoir compris la méthode. Comptez sur moi pour vous la ressasser...
Allez, c'est parti! Les lecteurs qui ont déjà tout compris peuvent allègrement zapper la fin de cette notule... et les autres, tâchez d'ouvrir vos esgourdes et votre comprenote.
Or donc, on commence presque toujours la résolution d'une grille en sacrifiant deux cases isolées (colorées en bleu), avant d'entamer une série ininterrompue de coups gagnants (prenant les cases trois par trois et les colorant en jaune). Cette grille ayant 42 cases, si j'en sacrifie deux au départ ainsi que je viens de le préconiser, il en reste 40, nombre qui n'est pas multiple de 3 mais supérieur de 1 au multiple de 3 immédiatement inférieur (3 * 13 = 39, il faut ajouter 1 pour arriver à 40). A la fin de la partie, pour tomber juste, il faudra donc que je prenne un certain nombre de cases qui soit lui-même égal à un multiple de 3 majoré de 1, et comme (ça n'a rien à voir, mais je le sais aussi) le dernier coup d'une partie prend presque toujours un polygone convexe (un ensemble de cases réuni autour d'un sommet commun), ce polygone convexe devra donc lui aussi avoir un nombre de cases égal à un multiple de 3 majoré de 1. Tout cela est une façon bien compliquée (mais logique!) de dire que je devrai jouer le dernier coup sur un heptagone.
Ca, c'est le dernier coup de la partie, ce ne sera pas un coup gagnant et mon heptagone sera donc coloré en bleu. L'avant-dernier coup de la partie sera forcément joué à proximité immédiate de cet heptagone, et si je veux qu'il soit gagnant (et bien sûr que je le veux: c'est le but du jeu!) il faudra qu'il colore trois cases en jaune, donc il faudra que le polygone sur lequel je le jouerai soit marié à mon polygone final, c'est-à-dire qu'il ait avec lui deux cases en commun (regardez n'importe quelle grille et vous verrez que quand deux polygones ont des cases en commun, ce nombre est égal à deux sauf exceptions rarissimes). Deux cases en commun plus trois cases gagnantes = cinq cases, or un polygone réunissant cinq cases autour d'un sommet commun, ça s'appelle un pentagone. L'avant-dernier coup d'une partie à score optimal est joué sur un pentagone (et c'est toujours vrai... sauf cas très particuliers).
Assez radoté pour ce matin, à vous de jouer.
(et pour ceux qui n'ont pas la moindre idée de ce qu'il faut faire à ce stade: il faut dessiner un cavexe; mais ça, je ne vous l'expliquerai pas maintenant parce que c'est pas toujours à moi de travailler, vous n'avez qu'à rechercher dans les épisodes précédents ce que c'est qu'un cavexe, bande de flemmards)
Comme ça, à vue de nez, j'aurais tendance à dire qu'elle va être du même genre que la grille d'hier (elle a en tout cas le même nombre de cases, donc il faut la terminer de la même façon, sur un heptagone marié à un pentagone) -- et en la résolvant à l'instant, je l'ai trouvée plutôt facile. Question d'entraînement... A défaut d'autre chose, la rédaction de ce fil de discussion m'entraîne et même me mène à une certaine virtuosité -- qui n'impressionne personne, mais dont je suis quand même plutôt content.
Je suppose que vous l'aurez compris, les notules que je publie ici sont vouées à être reprises dans un petit ouvrage que je publierai sur Internet (sous une licence de libre diffusion, bien entendu -- la CC-BY, pour ceux qui connaissent les licences Creative Commons)... et Dieu sait ce que ça deviendra, mais j'ai quand même la certitude mathématique qu'il y aura encore dans mes grilles de quoi réjouir l'esprit de bargeots dans mon genre dans trois mille ans -- si l'humanité existe encore d'une part, si j'ai réussi à intéresser assez de monde à mes gamberges pour que le souvenir n'en disparaisse pas totalement, d'autre part. M'astreindre à alimenter ce fil tous les jours m'oblige à chercher plein d'exemples pédagogiques, à les creuser à fond et à travailler à leur lisibilité, tout en m'assurant que les solutions peuvent bel et bien être élaborées par des humains et non pas seulement des automatismes informatiques.
Aujourd'hui, il me paraît flagrant que la grille est très facile à résoudre de façon méthodique -- mais encore faut-il avoir compris la méthode. Comptez sur moi pour vous la ressasser...
Allez, c'est parti! Les lecteurs qui ont déjà tout compris peuvent allègrement zapper la fin de cette notule... et les autres, tâchez d'ouvrir vos esgourdes et votre comprenote.
Or donc, on commence presque toujours la résolution d'une grille en sacrifiant deux cases isolées (colorées en bleu), avant d'entamer une série ininterrompue de coups gagnants (prenant les cases trois par trois et les colorant en jaune). Cette grille ayant 42 cases, si j'en sacrifie deux au départ ainsi que je viens de le préconiser, il en reste 40, nombre qui n'est pas multiple de 3 mais supérieur de 1 au multiple de 3 immédiatement inférieur (3 * 13 = 39, il faut ajouter 1 pour arriver à 40). A la fin de la partie, pour tomber juste, il faudra donc que je prenne un certain nombre de cases qui soit lui-même égal à un multiple de 3 majoré de 1, et comme (ça n'a rien à voir, mais je le sais aussi) le dernier coup d'une partie prend presque toujours un polygone convexe (un ensemble de cases réuni autour d'un sommet commun), ce polygone convexe devra donc lui aussi avoir un nombre de cases égal à un multiple de 3 majoré de 1. Tout cela est une façon bien compliquée (mais logique!) de dire que je devrai jouer le dernier coup sur un heptagone.
Ca, c'est le dernier coup de la partie, ce ne sera pas un coup gagnant et mon heptagone sera donc coloré en bleu. L'avant-dernier coup de la partie sera forcément joué à proximité immédiate de cet heptagone, et si je veux qu'il soit gagnant (et bien sûr que je le veux: c'est le but du jeu!) il faudra qu'il colore trois cases en jaune, donc il faudra que le polygone sur lequel je le jouerai soit marié à mon polygone final, c'est-à-dire qu'il ait avec lui deux cases en commun (regardez n'importe quelle grille et vous verrez que quand deux polygones ont des cases en commun, ce nombre est égal à deux sauf exceptions rarissimes). Deux cases en commun plus trois cases gagnantes = cinq cases, or un polygone réunissant cinq cases autour d'un sommet commun, ça s'appelle un pentagone. L'avant-dernier coup d'une partie à score optimal est joué sur un pentagone (et c'est toujours vrai... sauf cas très particuliers).
Assez radoté pour ce matin, à vous de jouer.
(et pour ceux qui n'ont pas la moindre idée de ce qu'il faut faire à ce stade: il faut dessiner un cavexe; mais ça, je ne vous l'expliquerai pas maintenant parce que c'est pas toujours à moi de travailler, vous n'avez qu'à rechercher dans les épisodes précédents ce que c'est qu'un cavexe, bande de flemmards)
Dernière édition par Petitagore le Mer 9 Sep 2015 - 11:14, édité 1 fois (Raison : mot manquant)
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Pieyre Mar 24 Mar 2015 - 9:22
Mais si, moi ta virtuosité m'impressionne. Et, ce qui m'impressionne encore plus, c'est que tu puisses la déployer seul. Bon, pas tout à fait seul puisque c'est devant un public ébahi, mais tout de même sans tellement de ces commentaires ou de ces objections qui personnellement me sont nécessaires pour avancer.
D'ailleurs, c'est amusant : je me suis dit justement hier que tu devrais publier tes recherches, puisqu'il n'y aura plus grand travail de mise en forme à y apporter.
Sinon, j'aurais des commentaires à faire sur les cas atypiques, mais ce sera après tes problèmes du jour.
D'ailleurs, c'est amusant : je me suis dit justement hier que tu devrais publier tes recherches, puisqu'il n'y aura plus grand travail de mise en forme à y apporter.
Sinon, j'aurais des commentaires à faire sur les cas atypiques, mais ce sera après tes problèmes du jour.
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Invité Mar 24 Mar 2015 - 13:10
Jolis casse-têtes.
Le temps de lire depuis le début, je n'avais pas encore vu ce genre-là, faut que je me mette à jour pour comprendre ce que c'est... Merci Petitagore pour le topic. Miam miam miam.
Je rattrape en cours de chemin dès que je peux, après la journée de travail.
C'est "la Semaine des Mathématiques" qui se prolonge...
Le temps de lire depuis le début, je n'avais pas encore vu ce genre-là, faut que je me mette à jour pour comprendre ce que c'est... Merci Petitagore pour le topic. Miam miam miam.
Je rattrape en cours de chemin dès que je peux, après la journée de travail.
C'est "la Semaine des Mathématiques" qui se prolonge...
Invité- Invité
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Mar 24 Mar 2015 - 19:20
Pieyre, Kara Magic whale, merci de me permettre de me sentir moins seul...
Merci du compliment, mais ça prouve que le message n'est pas encore passé: il s'agit beaucoup moins de virtuosité que de logique et de méthode. J'espère qu'au fil des jours j'arriverai à vous en convaincre...
Par ailleurs, je ne suis pas exactement seul, car mon solveur stimule bien ma créativité en me suggérant des multitudes de solutions, parfois très élégantes. C'est donc à lui (et à la logique éternelle et incréée qui se cache derrière) que doivent aller une grande part de vos compliments.
Bon, alors, cette grille "novembre", comment la résoudre de façon logique et méthodique? Il y a plusieurs possibilités, mais voici celle qui me paraît la plus pédagogique:
La figure est double, parce que le premier cavexe est celui qui tombe sous le sens (si, si, vous allez voir), et le deuxième le retravaille pour le rendre encore plus facile d'emploi.
Vous l'avez compris, il nous faut d'abord viser un heptagone marié à un pentagone. Pourquoi chercher midi à quatorze heures, colorions en bleu le bel heptagone qui se voit comme le nez au milieu de la figure, par exemple en cliquant 14, 15, 23, 8 et 21.
Muy bien. Cet heptagone n'est marié qu'à un pentagone, dont je vais colorier trois cases en jaune en cliquant sur 27.
A partir de là, deux façons de continuer: un clic sur 12 pour colorer en jaune 13, 12 et 19, ou un clic sur 30 pour colorer en jaune 29, 30 et 31. La première solution est préférable, car on peut tout de suite achever derrière un beau cavexe horizontal, en cliquant sur 17, ce qui prend simultanément les cases 16, 17 et 18 et nous dessine le cavexe ci-dessus représenté dans la moitié gauche de l'image.
On pourrait trouver que c'est un travail suffisant, s'efforcer de photographier mentalement cette forme, vider la grille avec la touche de magnétophone la plus à gauche et attaquer la résolution à partir d'une grille vide. On pourrait. Mais je crois préférable de rendre le cavexe plus rondouillard et patatoïde, en cliquant encore sur 30 (qui prend 29, 30 et 31), puis 24 (qui prend 32, 24 et 25).
Le patatoïde ainsi obtenu (moitié droite de l'image ci-dessus) est très facile à mémoriser: c'est toute la grille, moins une rangée horizontale en haut de la grille et une rangée horizontale en bas (si comme moi vous jouez aux échecs, vous devez trouver que "rangée horizontale" est un pléonasme redondant... c'est pas grave, c'est plus clair comme ça).
Donc, votre mission est de jouer les premiers coups de façon à prendre toutes les cases de ces deux rangées et rien d'autre. Ce qui n'est pas bien malin. Par exemple: 7 3 1 36 26 6 5 39. Et voilà mon cavexe patatoïde dessiné en inversant la forme que nous avions identifiée.
Et à partir de là, ben yapuka faire comme prévu, c'est-à-dire absolument la même chose que pour dessiner le cavexe, mais en ordre inverse. Et ça peut nous donner: 24 30 17 12 27 (fin des coups gagnants jaunes), et le dernier coup, indifférent comme l'est presque toujours le dernier coup, colorera l'heptagone final en bleu, comme prévu.
Virtuosité? Que nenni: logique, méthode, distzipline. Un adjudant-chef prussien ne s'y serait pas pris autrement.
Je vais revenir pour vous indiquer des solutions plus rigolotes, mais celle-là est irréprochable.
Pieyre a écrit:Mais si, moi ta virtuosité m'impressionne. Et, ce qui m'impressionne encore plus, c'est que tu puisses la déployer seul.
Merci du compliment, mais ça prouve que le message n'est pas encore passé: il s'agit beaucoup moins de virtuosité que de logique et de méthode. J'espère qu'au fil des jours j'arriverai à vous en convaincre...
Par ailleurs, je ne suis pas exactement seul, car mon solveur stimule bien ma créativité en me suggérant des multitudes de solutions, parfois très élégantes. C'est donc à lui (et à la logique éternelle et incréée qui se cache derrière) que doivent aller une grande part de vos compliments.
Bon, alors, cette grille "novembre", comment la résoudre de façon logique et méthodique? Il y a plusieurs possibilités, mais voici celle qui me paraît la plus pédagogique:
La figure est double, parce que le premier cavexe est celui qui tombe sous le sens (si, si, vous allez voir), et le deuxième le retravaille pour le rendre encore plus facile d'emploi.
Vous l'avez compris, il nous faut d'abord viser un heptagone marié à un pentagone. Pourquoi chercher midi à quatorze heures, colorions en bleu le bel heptagone qui se voit comme le nez au milieu de la figure, par exemple en cliquant 14, 15, 23, 8 et 21.
Muy bien. Cet heptagone n'est marié qu'à un pentagone, dont je vais colorier trois cases en jaune en cliquant sur 27.
A partir de là, deux façons de continuer: un clic sur 12 pour colorer en jaune 13, 12 et 19, ou un clic sur 30 pour colorer en jaune 29, 30 et 31. La première solution est préférable, car on peut tout de suite achever derrière un beau cavexe horizontal, en cliquant sur 17, ce qui prend simultanément les cases 16, 17 et 18 et nous dessine le cavexe ci-dessus représenté dans la moitié gauche de l'image.
On pourrait trouver que c'est un travail suffisant, s'efforcer de photographier mentalement cette forme, vider la grille avec la touche de magnétophone la plus à gauche et attaquer la résolution à partir d'une grille vide. On pourrait. Mais je crois préférable de rendre le cavexe plus rondouillard et patatoïde, en cliquant encore sur 30 (qui prend 29, 30 et 31), puis 24 (qui prend 32, 24 et 25).
Le patatoïde ainsi obtenu (moitié droite de l'image ci-dessus) est très facile à mémoriser: c'est toute la grille, moins une rangée horizontale en haut de la grille et une rangée horizontale en bas (si comme moi vous jouez aux échecs, vous devez trouver que "rangée horizontale" est un pléonasme redondant... c'est pas grave, c'est plus clair comme ça).
Donc, votre mission est de jouer les premiers coups de façon à prendre toutes les cases de ces deux rangées et rien d'autre. Ce qui n'est pas bien malin. Par exemple: 7 3 1 36 26 6 5 39. Et voilà mon cavexe patatoïde dessiné en inversant la forme que nous avions identifiée.
Et à partir de là, ben yapuka faire comme prévu, c'est-à-dire absolument la même chose que pour dessiner le cavexe, mais en ordre inverse. Et ça peut nous donner: 24 30 17 12 27 (fin des coups gagnants jaunes), et le dernier coup, indifférent comme l'est presque toujours le dernier coup, colorera l'heptagone final en bleu, comme prévu.
Virtuosité? Que nenni: logique, méthode, distzipline. Un adjudant-chef prussien ne s'y serait pas pris autrement.
Je vais revenir pour vous indiquer des solutions plus rigolotes, mais celle-là est irréprochable.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Mar 24 Mar 2015 - 20:15
Pour résoudre la grille "novembre", un autre cavexe horizontal était envisageable:
Les deux cavexes verticaux qui suivent ne sont pas très élégants, mais cela dit parfaitement exploitables:
J'en ai encore quelques-uns plus bizarroïdes sous le coude, mais je ne vais pas vous les indiquer tout de suite, il faut que j'aille aux fourneaux.
- Solution complète:
- 8 28 21 19 18 24 31 16 5 6 (hors du cavexe), 39 38 37 35 (dedans).
Les deux cavexes verticaux qui suivent ne sont pas très élégants, mais cela dit parfaitement exploitables:
- Solutions complètes:
- Avec le cavexe 1: 13 24 19 16 0 34 6 2 (hors du cavexe), 4 39 38 29 28 22 (dedans).
Avec le cavexe 2: 33 18 7 40 16 4 31 29 3 (hors du cavexe), 1 26 12 27 23 (dedans).
J'en ai encore quelques-uns plus bizarroïdes sous le coude, mais je ne vais pas vous les indiquer tout de suite, il faut que j'aille aux fourneaux.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Invité Mar 24 Mar 2015 - 22:08
22h, j'attaque enfin. Ah la vie de famille. ^^
Le lien interactif programmé au début buggue sur mon ordi, je ne vois qu'un écran quasi-blanc. Je désinstalle et réinstalle le navigateur pour voir. Faut-il un truc spécial ?
Mais si on peut tout faire avec méthode comme je crois le lire, au crayon et papier ça ira très bien. C'est ma méthode préférée avec le mental qui rubicube et classe.
Par curiosité j'irai demander à mon superman, il sait tout résoudre dans les "ça-marche-pas"...
Les premières questions sur les 3 côtés entiers, ça va, ouf.
Je replonge sur le sérieux qui suit.
EDIT: oki, ça marche. Rien sur internet, mais mozzilla désinstallé (il bugguait tout seul ces jours-ci) + réinstallé et ça marche nickel.
EDIT2: j'ai bien ri au raccourci "hexagones" de 6 triangles qui ont 5 côtés pourtant... Je suis dans la page 2, phase éponge pour s'imprégner du truc et tester sur le programme les "effets divers", ou en mentalisation du processus + lecture rapide de l'ensemble des pages en premier jet. Minuit, le bal des citrouilles-cavexes, dodo. ^^
Le lien interactif programmé au début buggue sur mon ordi, je ne vois qu'un écran quasi-blanc. Je désinstalle et réinstalle le navigateur pour voir. Faut-il un truc spécial ?
Mais si on peut tout faire avec méthode comme je crois le lire, au crayon et papier ça ira très bien. C'est ma méthode préférée avec le mental qui rubicube et classe.
Par curiosité j'irai demander à mon superman, il sait tout résoudre dans les "ça-marche-pas"...
Les premières questions sur les 3 côtés entiers, ça va, ouf.
Je replonge sur le sérieux qui suit.
EDIT: oki, ça marche. Rien sur internet, mais mozzilla désinstallé (il bugguait tout seul ces jours-ci) + réinstallé et ça marche nickel.
EDIT2: j'ai bien ri au raccourci "hexagones" de 6 triangles qui ont 5 côtés pourtant... Je suis dans la page 2, phase éponge pour s'imprégner du truc et tester sur le programme les "effets divers", ou en mentalisation du processus + lecture rapide de l'ensemble des pages en premier jet. Minuit, le bal des citrouilles-cavexes, dodo. ^^
Dernière édition par Kara Magic whale le Mer 25 Mar 2015 - 0:08, édité 1 fois
Invité- Invité
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Mar 24 Mar 2015 - 23:19
Bon, je termine cette étude de la résolution de la grille "novembre" par quelques cavexes bizarroïdes imaginés par mon solveur:
Je crois qu'aucun humain n'aurait des idées aussi tordues, mais une fois qu'on a identifié ces drôles de cavexes, eh bien ma foi on peut effectivement résoudre la grille en redessinant leurs formes:
Parmi ses idées tordues, mon solveur a aussi très brillamment imaginé ce cavexe oblique et torsadé: au lieu d'entourer le tore horizontalement ou verticalement comme tous ceux que j'imagine, il dessine une torsade autour. C'est vraiment une idée tordue (c'est le cas de le dire), mais elle n'est pas absurde:
Il est quand même achement fort, mon solveur, non? Par moments, je le prendrais presque pour Dieu omniscient... C'est pas lui, mais c'est vraiment pas mal imité.
Du coup, quand le solveur et moi trouvons le même optimum (ce qui arrive quand même assez souvent), j'ai vraiment l'impression de tenir tête à l'ange de la logique, tel Jacob au chapitre 32 de la Genèse. Ce qui, façon Eugène Delacroix à Saint-Sulpice, donne ceci:
Trouvez l'optimum sur une grille Triancey et vous aurez pareillement le droit de vous sentir "fort contre Dieu": car un optimum est par définition insurpassable, fût-ce par Dieu en personne.
Oui, je me la pète... Ça sert à ça, les jeux logiques!
Je crois qu'aucun humain n'aurait des idées aussi tordues, mais une fois qu'on a identifié ces drôles de cavexes, eh bien ma foi on peut effectivement résoudre la grille en redessinant leurs formes:
- Solution bizarroïdes mais complètes:
- Avec le cavexe 3: 14 29 22 31 19 24 7 17 (hors du cavexe), 41 16 39 8 36 2 (dedans).
Avec le cavexe 4: 28 39 30 32 15 20 10 11 17 (hors du cavexe), 12 7 8 3 34 (dedans).
Avec le cavexe 5: 17 26 32 41 10 38 3 1 (hors du cavexe), 34 29 18 12 20 23 (dedans).
Avec le cavexe 6: 10 30 39 41 23 28 20 25 (hors du cavexe), 17 12 7 4 3 33 (dedans).
Parmi ses idées tordues, mon solveur a aussi très brillamment imaginé ce cavexe oblique et torsadé: au lieu d'entourer le tore horizontalement ou verticalement comme tous ceux que j'imagine, il dessine une torsade autour. C'est vraiment une idée tordue (c'est le cas de le dire), mais elle n'est pas absurde:
- Solution complète (et torsadée):
- 19 14 27 29 31 18 6 40 (hors du cavexe), 25 10 5 4 36 26 (dedans).
Il est quand même achement fort, mon solveur, non? Par moments, je le prendrais presque pour Dieu omniscient... C'est pas lui, mais c'est vraiment pas mal imité.
Du coup, quand le solveur et moi trouvons le même optimum (ce qui arrive quand même assez souvent), j'ai vraiment l'impression de tenir tête à l'ange de la logique, tel Jacob au chapitre 32 de la Genèse. Ce qui, façon Eugène Delacroix à Saint-Sulpice, donne ceci:
Trouvez l'optimum sur une grille Triancey et vous aurez pareillement le droit de vous sentir "fort contre Dieu": car un optimum est par définition insurpassable, fût-ce par Dieu en personne.
Oui, je me la pète... Ça sert à ça, les jeux logiques!
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Jeu 26 Mar 2015 - 0:00
Craignant de lasser les petits lecteurs de cette passionnante saga, je vais consacrer ma chronique du jour aux vignettes Panini.
Bon, je plaisante, même si les vignettes Panini dont vous voyez ci-dessus un échantillon ne sont pas absolument dépourvues de rapport avec mes grilles -- du moins dans mon cerveau malade; je vais y revenir.
Hier, j'avais l'ambition de varier les plaisirs en vous parlant d'un peu autre chose que des grilles de difficulté moyenne de mon inventaire, comme je l'ai fait au cours des jours derniers. Mais ce que je me proposais de faire n'avait rigoureusement rien à voir avec les trombines de fotbaleurs que j'ai, au temps lointain de mon adolescence boutonneuse, collectionnées dans les albums de l'éditeur italien Panini.
(Reconnaîtrez-vous dans l'image ci-dessus la sympathique bobine de Dominique Rocheteau, le Zlatan Ibrahimovic des années 70? Ne le confondez pas avec le mec à moustaches, car ce dernier, c'est Raymond Domenech.)
En fait, hier, je voulais vous expliquer ce que j'entends par "cinq ou huit" (vous avez peut-être noté cette mention dans l'inventaire des grilles que j'ai publié au début du mois). Hélas, je n'ai visiblement pas trouvé pour cela l'exemple pédagogique que j'espérais, et la grille "septembre" sur laquelle j'ai fait travailler mon infaillible solveur toute la journée d'hier s'est révélée une des plus difficiles qui se puissent rencontrer.
Du coup, je vais vous parler des vignettes Panini...
L'éditeur italien Panini (puisse Belzébuth le faire crever) utilise depuis des années, et ce dès l'époque de mon adolescence, une technique simple, géniale et profondément malhonnête pour rançonner les petits ados boutonneux: il leur vend pour un prix ridicule (c'était cinq francs à l'époque, si ma mémoire est bonne) un bel album où tout est prêt pour qu'on y colle joliment la collection complète des trombines de tous les fotbaleurs en vue du moment. Ça représente plusieurs dizaines de joueurs (disons deux cents pour fixer les idées), dont on peut donc se procurer les portraits en achetant chez le marchand de journaux des sachets contenant chacun cinq vignettes Panini, et vendus pas très cher (cinquante centimes de l'époque, toujours si ma mémoire est bonne). Deux cents joueurs divisés par des pochettes de cinq vignettes = 40 sachets de vignettes à cinquante centimes = 20 francs, ça va, c'est abordable.
Encore que, laissez-moi réfléchir deux secondes...
-- Mais attends, ça va pas, on n'aura jamais tous les joueurs rien qu'avec quarante sachets; il y aura évidemment des manquants et des doublons.
-- C'est pas grave, on se les échange entre nous dans la cour de récré, tu apportes les vignettes que tu as en double et je te les change contre celles que j'ai en double, et en rien de temps tout le monde aura la collection complète, on est quand même beaucoup dans la cour de récré à collectionner les vignettes Panini.
Ça a l'air logique... et puis c'est sympa, convivial et tout, ça permet aux malheureux surdoués frappés d'ostracisme de tisser des liens avec les condisciples qui aiment les fotbaleurs et qui n'en sont pas moins des êtres humains (encore que). Allez, d'accord, voici mes cinq francs pour acheter l'album Panini.
Sauf que M. Panini est un satané fils de pute d'enfoiré de bâtard, il te laisse croire que ses sachets de vignettes sont remplis au hasard... mais c'est absolument pas vrai!
Bien au contraire, c'est soigneusement calculé pour que tout le monde ait la vignette Raymond Domenech (dont tout le monde se fout) en quadruple et en quintuple, mais qu'absolument personne ne réussisse jamais à se procurer la vignette de Dominique Rocheteau, justement la seule que tout le monde avait envie d'avoir. Du coup, très vite, au marché noir de la cour de récré, on pourrait facilement avoir vingt Raymond Domenech pour cinq centimes, en revanche la vignette de Dominique Rocheteau se vendrait jusqu'à quarante francs si quelqu'un la trouvait.
Entre ces deux extrêmes, les probabilités d'apparition des trombines des fotbaleurs sont variables, et en général chaque ado boutonneux garde l'espoir de réussir à avoir presque la collec' complète (sauf Rocheteau, rêve inaccessible) pour une somme raisonnable. Bon, d'accord, pas pour 20 francs.
Pas pour quarante non plus, d'ailleurs.
Pas pour quatre-vingts non plus, à dire vrai.
Aux environs de 165 francs dépensés pour l'essentiel en pure perte, les ados (et leurs parents qui leur filent les sous) commencent à se rendre compte que c'est l'arnaque complète, que chaque ado a déjà flanqué soixante-cinq vignettes de Raymond Domenech à la poubelle sans que personne n'ait jamais vu la couleur d'une seule vignette Dominique Rocheteau. Honteux et confus, les ados jurent mais un peu tard qu'on ne les y reprendra plus, le proviseur interdit avec la plus grande fermeté l'échange de vignettes Panini dans la cour de récré, et ça se calme.
M. Panini laisse alors tomber le marché français mais refait aussitôt le coup en Espagne, puis au Portugal, puis en Allemagne, puis en Grande-Bretagne... Cinq ans plus tard, quand une nouvelle collection de vignettes Panini réapparaît dans la cour de récré, avec les tronches des fotbaleurs du moment, le nouveau proviseur ne connaît pas l'arnaque, tous les ados qui avaient juré mais un peu tard ont quitté le collège, et donc une nouvelle génération d'ados se fait posséder très exactement comme la précédente. M. Panini est vraiment un enculé de sa race.
(non, je ne suis pas homophobe, ni raciste: je suis en colère, c'est tout)
Bon. Et le rapport avec les grilles Triancey, me direz-vous?
Le rapport, c'est que quand je demande à mon solveur de trouver une solution élégante à la grille "septembre" (une solution qui me fait saliver d'avance, à la façon de la photo de Dominique Rocheteau), eh bien il me ressort cinquante fois de suite la même solution inélégante (aussi antipathique qu'une photo de Raymond Domenech). Or, de même que la pochette Panini coûte quand même cinquante centimes, l'élaboration d'une solution par mon solveur demande quand même environ trois minutes de calcul à ma machine. A la fin de la journée, j'ai donc bouffé quelques kilowatts-heure à retrouver sempiternellement ma solution moche-Raymond Domenech, sans jamais avoir vu la couleur d'une solution élégante-Dominique Rocheteau.
Et je me dis que, décidément, M. Panini est vraiment un sale macaroni de merde. Qu'il ne croise jamais mon chemin ou je lui arracherai les yeux et je lui ferai bouffer ses couilles.
(non, je ne suis ni xénophobe ni violent; seulement un tantinet exaspéré)
Or donc, non seulement la grille "septembre" se révèle particulièrement pauvre en cavexes, mais en plus aucun des quatre identifiés par mon solveur (et encore ai-je dû, pour trouver la quatrième, faire travailler ma machine... disons pour un coût équivalent à celui de vingt-cinq pochettes Panini)... eh bien aucun de ces cavexes n'est "réversible": aucun n'est susceptible d'être dessiné comme j'ai coutume de le faire, c'est-à-dire en ordre chronologique inverse, avec le polygone final en bleu et les autres cases du cavexe colorées trois par trois en jaune -- ce joli coloriage pédagogique étant d'ordinaire effectué avec les mêmes automatismes informatiques que pour jouer normalement.
Sur l'image que je publie ci-dessous, les immondes cavexes de la grille "septembre" sont donc par exception représentés par les cases noires, les autres figurant le début de la partie.
Vous pouvez quand même essayer de résoudre cette grille sur la base de ces quatre cavexes. Mais si vous trouvez ça particulièrement infaisable, faites-moi plaisir: ne m'en faites pas grief.
Tout ça, c'est la faute à Panini. Je hais Panini.
Bon, je plaisante, même si les vignettes Panini dont vous voyez ci-dessus un échantillon ne sont pas absolument dépourvues de rapport avec mes grilles -- du moins dans mon cerveau malade; je vais y revenir.
Hier, j'avais l'ambition de varier les plaisirs en vous parlant d'un peu autre chose que des grilles de difficulté moyenne de mon inventaire, comme je l'ai fait au cours des jours derniers. Mais ce que je me proposais de faire n'avait rigoureusement rien à voir avec les trombines de fotbaleurs que j'ai, au temps lointain de mon adolescence boutonneuse, collectionnées dans les albums de l'éditeur italien Panini.
(Reconnaîtrez-vous dans l'image ci-dessus la sympathique bobine de Dominique Rocheteau, le Zlatan Ibrahimovic des années 70? Ne le confondez pas avec le mec à moustaches, car ce dernier, c'est Raymond Domenech.)
En fait, hier, je voulais vous expliquer ce que j'entends par "cinq ou huit" (vous avez peut-être noté cette mention dans l'inventaire des grilles que j'ai publié au début du mois). Hélas, je n'ai visiblement pas trouvé pour cela l'exemple pédagogique que j'espérais, et la grille "septembre" sur laquelle j'ai fait travailler mon infaillible solveur toute la journée d'hier s'est révélée une des plus difficiles qui se puissent rencontrer.
Du coup, je vais vous parler des vignettes Panini...
L'éditeur italien Panini (puisse Belzébuth le faire crever) utilise depuis des années, et ce dès l'époque de mon adolescence, une technique simple, géniale et profondément malhonnête pour rançonner les petits ados boutonneux: il leur vend pour un prix ridicule (c'était cinq francs à l'époque, si ma mémoire est bonne) un bel album où tout est prêt pour qu'on y colle joliment la collection complète des trombines de tous les fotbaleurs en vue du moment. Ça représente plusieurs dizaines de joueurs (disons deux cents pour fixer les idées), dont on peut donc se procurer les portraits en achetant chez le marchand de journaux des sachets contenant chacun cinq vignettes Panini, et vendus pas très cher (cinquante centimes de l'époque, toujours si ma mémoire est bonne). Deux cents joueurs divisés par des pochettes de cinq vignettes = 40 sachets de vignettes à cinquante centimes = 20 francs, ça va, c'est abordable.
Encore que, laissez-moi réfléchir deux secondes...
-- Mais attends, ça va pas, on n'aura jamais tous les joueurs rien qu'avec quarante sachets; il y aura évidemment des manquants et des doublons.
-- C'est pas grave, on se les échange entre nous dans la cour de récré, tu apportes les vignettes que tu as en double et je te les change contre celles que j'ai en double, et en rien de temps tout le monde aura la collection complète, on est quand même beaucoup dans la cour de récré à collectionner les vignettes Panini.
Ça a l'air logique... et puis c'est sympa, convivial et tout, ça permet aux malheureux surdoués frappés d'ostracisme de tisser des liens avec les condisciples qui aiment les fotbaleurs et qui n'en sont pas moins des êtres humains (encore que). Allez, d'accord, voici mes cinq francs pour acheter l'album Panini.
Sauf que M. Panini est un satané fils de pute d'enfoiré de bâtard, il te laisse croire que ses sachets de vignettes sont remplis au hasard... mais c'est absolument pas vrai!
Bien au contraire, c'est soigneusement calculé pour que tout le monde ait la vignette Raymond Domenech (dont tout le monde se fout) en quadruple et en quintuple, mais qu'absolument personne ne réussisse jamais à se procurer la vignette de Dominique Rocheteau, justement la seule que tout le monde avait envie d'avoir. Du coup, très vite, au marché noir de la cour de récré, on pourrait facilement avoir vingt Raymond Domenech pour cinq centimes, en revanche la vignette de Dominique Rocheteau se vendrait jusqu'à quarante francs si quelqu'un la trouvait.
Entre ces deux extrêmes, les probabilités d'apparition des trombines des fotbaleurs sont variables, et en général chaque ado boutonneux garde l'espoir de réussir à avoir presque la collec' complète (sauf Rocheteau, rêve inaccessible) pour une somme raisonnable. Bon, d'accord, pas pour 20 francs.
Pas pour quarante non plus, d'ailleurs.
Pas pour quatre-vingts non plus, à dire vrai.
Aux environs de 165 francs dépensés pour l'essentiel en pure perte, les ados (et leurs parents qui leur filent les sous) commencent à se rendre compte que c'est l'arnaque complète, que chaque ado a déjà flanqué soixante-cinq vignettes de Raymond Domenech à la poubelle sans que personne n'ait jamais vu la couleur d'une seule vignette Dominique Rocheteau. Honteux et confus, les ados jurent mais un peu tard qu'on ne les y reprendra plus, le proviseur interdit avec la plus grande fermeté l'échange de vignettes Panini dans la cour de récré, et ça se calme.
M. Panini laisse alors tomber le marché français mais refait aussitôt le coup en Espagne, puis au Portugal, puis en Allemagne, puis en Grande-Bretagne... Cinq ans plus tard, quand une nouvelle collection de vignettes Panini réapparaît dans la cour de récré, avec les tronches des fotbaleurs du moment, le nouveau proviseur ne connaît pas l'arnaque, tous les ados qui avaient juré mais un peu tard ont quitté le collège, et donc une nouvelle génération d'ados se fait posséder très exactement comme la précédente. M. Panini est vraiment un enculé de sa race.
(non, je ne suis pas homophobe, ni raciste: je suis en colère, c'est tout)
Bon. Et le rapport avec les grilles Triancey, me direz-vous?
Le rapport, c'est que quand je demande à mon solveur de trouver une solution élégante à la grille "septembre" (une solution qui me fait saliver d'avance, à la façon de la photo de Dominique Rocheteau), eh bien il me ressort cinquante fois de suite la même solution inélégante (aussi antipathique qu'une photo de Raymond Domenech). Or, de même que la pochette Panini coûte quand même cinquante centimes, l'élaboration d'une solution par mon solveur demande quand même environ trois minutes de calcul à ma machine. A la fin de la journée, j'ai donc bouffé quelques kilowatts-heure à retrouver sempiternellement ma solution moche-Raymond Domenech, sans jamais avoir vu la couleur d'une solution élégante-Dominique Rocheteau.
Et je me dis que, décidément, M. Panini est vraiment un sale macaroni de merde. Qu'il ne croise jamais mon chemin ou je lui arracherai les yeux et je lui ferai bouffer ses couilles.
(non, je ne suis ni xénophobe ni violent; seulement un tantinet exaspéré)
Or donc, non seulement la grille "septembre" se révèle particulièrement pauvre en cavexes, mais en plus aucun des quatre identifiés par mon solveur (et encore ai-je dû, pour trouver la quatrième, faire travailler ma machine... disons pour un coût équivalent à celui de vingt-cinq pochettes Panini)... eh bien aucun de ces cavexes n'est "réversible": aucun n'est susceptible d'être dessiné comme j'ai coutume de le faire, c'est-à-dire en ordre chronologique inverse, avec le polygone final en bleu et les autres cases du cavexe colorées trois par trois en jaune -- ce joli coloriage pédagogique étant d'ordinaire effectué avec les mêmes automatismes informatiques que pour jouer normalement.
Sur l'image que je publie ci-dessous, les immondes cavexes de la grille "septembre" sont donc par exception représentés par les cases noires, les autres figurant le début de la partie.
Vous pouvez quand même essayer de résoudre cette grille sur la base de ces quatre cavexes. Mais si vous trouvez ça particulièrement infaisable, faites-moi plaisir: ne m'en faites pas grief.
Tout ça, c'est la faute à Panini. Je hais Panini.
- Solutions complètes:
- Avec le cavexe à mortaise 0, et aussi en démarrant à partir de deux cases isolées dans deux quadrilatères éloignés (technique très fûtée et élégante): 3 14 11 22 13 25 0 18 33 23 (hors du cavexe), 32 31 37 45 5 42 (dedans).
Avec le cavexe à mortaise 1: 24 2 4 32 17 13 40 21 0 (hors du cavexe), 14 16 38 37 7 41 43 (dedans).
Avec le cavexe à mortaise 2: 22 14 11 3 13 25 40 (hors du cavexe), 0 10 24 29 38 7 5 42 35 (dedans).
Avec le cavexe à mortaise 3: 10 0 2 12 15 21 26 19 33 (hors du cavexe), 32 23 31 28 7 5 43 (dedans).
Dernière édition par Petitagore le Jeu 26 Mar 2015 - 0:12, édité 1 fois (Raison : légère gourrance)
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Jeu 26 Mar 2015 - 14:25
Bon, assez déblatéré sur les escrocs italiens, je reviens sur le sujet des grilles "cinq ou huit".
La théorie, que je vous ressasse à chaque fois que je vous présente une grille, c'est que le score optimal en cases jaunes est atteint quand la grille est presque entièrement jaune, avec pour seules exceptions: 1) deux cases bleues sacrifiées au début; 2) un polygone convexe sacrifié au dernier coup (et donc coloré en bleu). Ce polygone final, ai-je coutume d'ajouter, doit être sauf exceptions un pentagone, un hexagone ou un heptagone, en fonction de ce qui est nécessaire pour que le nombre de cases jaunes (prises entre les deux coups initiaux et le polygone convexe final) soit un multiple de trois -- puisque les cases ne sont colorées en jaune que quand elles sont prises exactement par trois, c'est le principe même du jeu.
Je dis bien: "sauf exceptions". Ça veut donc dire qu'il y a des exceptions... Nous en avons déjà vu une: une résolution classique de la grille "mai" n'est pas possible et, comme nous l'avons vu alors, c'est relativement facile à démontrer. De par son nombre de cellules (40 = 2 cases sacrifiées au début + 38, qui est un multiple de 3 majoré de 2), cette grille devrait dans l'idéal voire sa résolution s'achever sur un pentagone, c'est-à-dire le plus petit polygone convexe dont le nombre de cases soit lui-même un multiple de 3 majoré de 2, mais comme c'était en l'occurrence impossible (reportez-vous éventuellement à ce que j'ai déjà expliqué à cette occasion), il fallait jouer un coup gagnant de moins et donc sacrifier au coup final non pas cinq cases, mais trois de plus, c'est-à-dire huit.
Dans ce cas-là, nous avions de la chance, on pouvait démontrer sans peine qu'il était impossible de terminer sur cinq cases. Symétriquement, il y a des grilles sur lesquelles on peut démontrer sans peine qu'il est possible de ne sacrifier qu'un pentagone au dernier coup (comment? mais tout simplement en trouvant très vite une solution "classique"!).
Seulement, entre ces deux situations idéales, il y a beaucoup de cas tangents, où l'être humain normal ne sait répondre ni "c'est possible" ni "c'est impossible", mais seulement des trucs foireux et provisoires du genre "jusqu'à plus ample informé, il me paraît présomptueux de l'exclure" ou "j'ai tellement essayé sans réussir que je suis quasi certain que c'est impossible".
Ces cas foireux, je les appelle des "cinq ou huit" (il est très rare qu'on rencontre des "quatre ou sept", rarissime d'être en présence de "six ou neuf", même si c'est également concevable avec des nombres de cases différents), et je ne peux avoir de certitude à leur sujet qu'en faisant tourner mon solveur (supposé infaillible). Par exemple, sur l'exemple excessivement difficile que je vous ai montré hier, la grille "aout", j'aurais juré qu'il n'était pas possible de terminer sur un pentagone tellement je m'y étais cassé les dents, mais mon solveur a quand même trouvé quatre façons (certes inélégantes, mais valides) d'y parvenir.
En revanche, sur la grille "prof" que je vous présente aujourd'hui...
... il faut terminer sur huit cases et non sur cinq, mon solveur est absolument formel... mais je n'ai pas vraiment de démonstration convaincante pour vous l'expliquer.
Je reviendrai donc tout à l'heure, non seulement avec des solutions s'achevant sur huit cases, mais aussi avec une démonstration pas très convaincante (c'est mieux que rien) de l'impossibilité de terminer sur cinq. Et je vous entretiendrai aussi, dans la foulée, des considérations philosophiques que cela doit nous inspirer (mes très chers frères...).
Entre-temps, je vous incite à faire deux choses:
- trouver un moyen d'atteindre l'optimum sur la grille (la résoudre, quoi), sachant que cet optimum est égal au nombre de cases minoré de 10 (2 cases sacrifiées au début, 8 à la fin... ou encore 3 et 7 si ça vous amuse, mais ce sera hétérodoxe); c'est assez facile si vous raisonnez bien, et ce même si vous ne vous donnez pas la peine d'élaborer soigneusement un cavexe au préalable comme pourtant je vous le recommande d'ordinaire;
- chercher un moyen d'expliquer pourquoi il n'est pas possible de terminer en ne sacrifiant que 7 cases (et donc en terminant sur un pentagone); c'est nettement plus difficile (moi-même, je doute d'en être vraiment capable... mais faut pas que ça vous bloque!).
Bon courage et à plus tard.
La théorie, que je vous ressasse à chaque fois que je vous présente une grille, c'est que le score optimal en cases jaunes est atteint quand la grille est presque entièrement jaune, avec pour seules exceptions: 1) deux cases bleues sacrifiées au début; 2) un polygone convexe sacrifié au dernier coup (et donc coloré en bleu). Ce polygone final, ai-je coutume d'ajouter, doit être sauf exceptions un pentagone, un hexagone ou un heptagone, en fonction de ce qui est nécessaire pour que le nombre de cases jaunes (prises entre les deux coups initiaux et le polygone convexe final) soit un multiple de trois -- puisque les cases ne sont colorées en jaune que quand elles sont prises exactement par trois, c'est le principe même du jeu.
Je dis bien: "sauf exceptions". Ça veut donc dire qu'il y a des exceptions... Nous en avons déjà vu une: une résolution classique de la grille "mai" n'est pas possible et, comme nous l'avons vu alors, c'est relativement facile à démontrer. De par son nombre de cellules (40 = 2 cases sacrifiées au début + 38, qui est un multiple de 3 majoré de 2), cette grille devrait dans l'idéal voire sa résolution s'achever sur un pentagone, c'est-à-dire le plus petit polygone convexe dont le nombre de cases soit lui-même un multiple de 3 majoré de 2, mais comme c'était en l'occurrence impossible (reportez-vous éventuellement à ce que j'ai déjà expliqué à cette occasion), il fallait jouer un coup gagnant de moins et donc sacrifier au coup final non pas cinq cases, mais trois de plus, c'est-à-dire huit.
Dans ce cas-là, nous avions de la chance, on pouvait démontrer sans peine qu'il était impossible de terminer sur cinq cases. Symétriquement, il y a des grilles sur lesquelles on peut démontrer sans peine qu'il est possible de ne sacrifier qu'un pentagone au dernier coup (comment? mais tout simplement en trouvant très vite une solution "classique"!).
Seulement, entre ces deux situations idéales, il y a beaucoup de cas tangents, où l'être humain normal ne sait répondre ni "c'est possible" ni "c'est impossible", mais seulement des trucs foireux et provisoires du genre "jusqu'à plus ample informé, il me paraît présomptueux de l'exclure" ou "j'ai tellement essayé sans réussir que je suis quasi certain que c'est impossible".
Ces cas foireux, je les appelle des "cinq ou huit" (il est très rare qu'on rencontre des "quatre ou sept", rarissime d'être en présence de "six ou neuf", même si c'est également concevable avec des nombres de cases différents), et je ne peux avoir de certitude à leur sujet qu'en faisant tourner mon solveur (supposé infaillible). Par exemple, sur l'exemple excessivement difficile que je vous ai montré hier, la grille "aout", j'aurais juré qu'il n'était pas possible de terminer sur un pentagone tellement je m'y étais cassé les dents, mais mon solveur a quand même trouvé quatre façons (certes inélégantes, mais valides) d'y parvenir.
En revanche, sur la grille "prof" que je vous présente aujourd'hui...
... il faut terminer sur huit cases et non sur cinq, mon solveur est absolument formel... mais je n'ai pas vraiment de démonstration convaincante pour vous l'expliquer.
Je reviendrai donc tout à l'heure, non seulement avec des solutions s'achevant sur huit cases, mais aussi avec une démonstration pas très convaincante (c'est mieux que rien) de l'impossibilité de terminer sur cinq. Et je vous entretiendrai aussi, dans la foulée, des considérations philosophiques que cela doit nous inspirer (mes très chers frères...).
Entre-temps, je vous incite à faire deux choses:
- trouver un moyen d'atteindre l'optimum sur la grille (la résoudre, quoi), sachant que cet optimum est égal au nombre de cases minoré de 10 (2 cases sacrifiées au début, 8 à la fin... ou encore 3 et 7 si ça vous amuse, mais ce sera hétérodoxe); c'est assez facile si vous raisonnez bien, et ce même si vous ne vous donnez pas la peine d'élaborer soigneusement un cavexe au préalable comme pourtant je vous le recommande d'ordinaire;
- chercher un moyen d'expliquer pourquoi il n'est pas possible de terminer en ne sacrifiant que 7 cases (et donc en terminant sur un pentagone); c'est nettement plus difficile (moi-même, je doute d'en être vraiment capable... mais faut pas que ça vous bloque!).
Bon courage et à plus tard.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Invité Jeu 26 Mar 2015 - 17:42
Petitagore, tu préfères qu'on saute le suivi des pages pour arriver direct ici, ou tu conseilles de faire depuis le début ?
Invité- Invité
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Jeu 26 Mar 2015 - 19:24
Kara Magic whale a écrit:Petitagore, tu préfères qu'on saute le suivi des pages pour arriver direct ici, ou tu conseilles de faire depuis le début ?
Oh, moi je préférerais que vous lisiez au moins les premières pages... Mais considérant que la répétition est la base même de la pédagogie, je fais de toute façon d'énormes efforts pour dire trente-sept fois de suite les choses essentielles en essayant de varier un peu les formulations (même que ça commence à me pomper l'air, mais je continuerai jusqu'à ce que quelqu'un me demande de me taire!).
Par ailleurs, je me suis mis à inclure des auto-références dans mes posts (des liens bleus vers des posts antérieurs), pas de façon systématique parce que c'est quand même du travail, mais je crois que je vais le faire de plus en plus souvent. Donc je pense qu'on peut sans trop de peine prendre le film en route, même si ce n'est pas recommandé.
Enfin, quand je fais exprès de dire des bêtises (je ne fais pas toujours exprès), comme hier dans ma notule sur les vignettes Panini, je pense que ces sottises, ou bien vous feront rire par elles-mêmes (j'espère), ou bien ne vous feront pas rire du tout (et dans ce cas, il vaut peut-être mieux que vous ne lisiez pas les posts antérieurs: comme disait ma grand-mère, les meilleures plaisanteries sont les plus courtes, surtout quand elles ne sont pas drôles).
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Jeu 26 Mar 2015 - 20:04
Bon. Primum solutionem trouvare, deinde philosophare (1). Si vous croyez mon solveur sur parole sur le point qu'il faut terminer la résolution de la grille "prof" qui nous occupe aujourd'hui en sacrifiant huit cases... yaka y aller gaiement sans trop se casser la tête, car en général les grilles où le coup final prend huit cases sont très faciles à résoudre (c'était flagrant lors de la résolution de la grille "mai", si vous vous souvenez). Au temps de mon service militaire, mon capitaine instructeur aurait certainement dit que les grilles qui se terminent sur la prise de huit cases, "on peut les attaquer avec sa bite et son couteau".
Ça ne nous dispense quand même pas de tout effort de réflexion. Qu'est-ce qui peut représenter un ensemble de huit cases prenables en un seul coup final? En général, le plus simple est un couloir de huit cases qui traverse le tore de part en part, mais pas de pot, sur cette grille, on ne peut pas en trouver un. En revanche, il y a un octogone (un seul), même s'il ne se voit pas beaucoup, réparti qu'il est sur les côtés gauche et droit du tore: 24, 32, 38, 37 sur le côté gauche, 31, 36, 44, 45 sur le côté droit. L'octogone, ce sera le dernier coup de la partie, mais l'avant-dernier coup de la partie, ce sera classiquement un pentagone marié à cet octogone par deux cases... c'est-à-dire les cases 28, 29 et 30 (que nous prendrons par un coup gagnant jaune) ainsi que 36 et 31 (qui seront prises en bleu au coup final, en même temps que l'ensemble de l'octogone).
Nous en savons assez, à l'attaque!
Voici ma solution à moi, et elle a bien dû me demander quarante secondes de tâtonnements: 43 26 35 40 18 3 10 12 6 15 23 21 1 29 32.
Mon solveur peut vous en suggérer plein d'autres, toutes plus inélégantes les unes que les autres, correspondant à ces affreux cavexes à mortaise, non inversibles (reportez-vous aux épisodes précédents):
Vous exigez une solution élégante, avec un beau cavexe rondouillard? Oh, écoutez, ça me gonfle de vous expliquer, c'est trop simple. Je vous donne juste la photo du cavexe, débrouillez-vous:
Donc, on est d'accord, terminer en sacrifiant huit cases, c'est vraiment très facile (du moins dans la plupart des cas) -- beaucoup plus facile, en tout cas, que de terminer sur un pentagone. Rappelez-vous quelle galère ça a été sur la grille d'hier.
-- Ben pourquoi ne pas toujours terminer sur huit cases, alors?
-- Parce que le but du jeu est de trouver l'optimum de cases jaunes, pas un optimum au rabais. Terminer sur huit quand on peut terminer sur cinq, c'est déchoir, mon cher fils.
-- Ben pourquoi vous terminez pas sur cinq ce coup-ci, alors?
-- Parce que ça n'est pas possible.
-- Et qu'est-ce que vous en savez?
-- Je le sais parce que mon solveur a essayé et n'y est pas parvenu.
-- Et qui vous dit que votre solveur n'est pas truffé de bugs? C'est vous qui l'avez écrit et, hum, sans vouloir vous vexer, mon cher maître, vous avez déjà eu l'humilité de reconnaître que vous n'êtes point infaillible.
-- Je ne suis peut-être pas infaillible en toutes circonstances, mais je vous le déclare bien haut, ex cathedra, du haut de ma chaire pontificale triancesque, on ne peut pas atteindre l'optimum de la grille "prof" en terminant sur un pentagone.
-- Je déteste les énoncés dogmatiques. On ne peut pas because?
-- Because c'est comme ça et je le sais.
-- Et si vous vous trompiez, cher maître? Car après tout, la grille "prof" comporte bien deux pentagones mariés -- contrairement à la grille "mai" que vous aviez cette fois légitimement, j'en conviens volontiers, terminé en sacrifiant huit cases.
-- Mais tu les vois où, tes pentagones mariés, petit connard?
-- Ici, cher maître. Premier pentagone 28, 29, 30, 31, 36; second pentagone 30, 31... 22, 23, 24.
-- Ah. En effet.
Eh bien oui, c'est ça le problème avec les "cinq ou huit": on n'a pas toujours à sa disposition de preuve mathématique démontrant l'impossibilité absolue de terminer en ne sacrifiant que cinq cases. Mon solveur me fournit des preuves informatiques, mais moi non plus elles ne me satisfont pas complètement, et moi aussi j'ai un tempérament qui m'incite à demander... la preuve de la preuve.
Alors je vais essayer. Regardez ci-dessus les deux pentagones mariés, correspondant aux deux derniers coups de la partie, et demandez-vous quel pourrait être l'antépénultième coup de la partie qui pourrait être joué avant la prise de ce coacervat final. Ce coup antépénultième ne prendrait donc, par hypothèse, que trois cases (sans quoi ça ne serait pas un coup gagnant). Or on peut faire valoir qu'aucun des polygones mariés par deux cases à ce coacervat final (par exemple l'heptagone 20, 19, 26, 27, 35, plus les deux cases 28 et 29 déjà dans le coacervat) n'est un pentagone. Ce n'est pas une preuve formelle, mais c'est un indice fort.
-- Mais l'antépénultième coup pourrait peut-être comporter une case isolée tenon-mortaise (note au lecteur: reportez-vous aux épisodes précédents) dans un hexagone marié avec le coacervat final, et par conséquent on pourrait quand même prendre trois cases en un coup.
-- Euh... Ce n'est peut-être pas inconcevable, mais ça me paraît quand même bien douteux. Et de toute façon, mon solveur dit que ça n'est pas possible sur cette grille.
-- Ou encore l'antépénultième coup pourrait prendre un petit couloir de trois cases.
-- Mmmmouiii... peut-être, en effet.
-- Mais pas en l'occurrence?
-- Il me semble que non.
-- Pourquoi?
-- Parce qu'il y a trop de cases dans la largeur de cette grille, qui est assez dense. Et par ailleurs, parce que mon solveur le dit.
-- Ça ne me convainc pas.
-- Homme de peu de foi...
Bon. Je crois qu'on n'en sortira pas.
L'honnêteté me force à dire que c'est peut-être là une faiblesse de mon jeu, en tout cas ce n'est pas conforme à la règle esthétique que je m'étais fixée: que l'optimum d'une grille puisse être déterminé sans erreur et sans peine. Cette faiblesse disparaîtrait peut-être en pratique si je diffusais le listing de mon solveur et le laissais vérifier par plein d'informaticiens compétents -- mais là encore, l'honnêteté me force à admettre que je l'ai écrit avec des techniques très inélégantes, que j'ai honte de montrer à quel point je m'y suis pris comme un manche; il faudrait que je trouve le courage de le réécrire proprement... mais ça me gonfle parce que tout moche qu'il est il m'a l'air de marcher très bien. J'applique donc l'adage informatique: if it ain't broke, don't fix it.
D'un autre côté, cette incertitude sur les quelques rares grilles "cinq ou huit" représente peut-être un avantage pour moi, car elle rend mon autorité pontificale absolument indispensable. Appelez-moi Eminence (non, pas Votre Sainteté, faut pas déconner quand même).
Mais c'est peut-être surtout -- et c'est en tout cas ainsi que je préfère le voir -- une école de vertu pour le joueur de ce casse-tête, qui peut certes se montrer très "fort contre la logique", mais ne peut quand même pas aller jusqu'à se prétendre "aussi fort que la logique". Cela met donc à sa disposition un exercice non pas seulement intellectuel, mais également moral, en lui demandant de temps à autre de chercher courageusement une solution qui n'existe peut-être pas, faute de quoi il risque de baisser les bras alors que la solution existait et pouvait être trouvée (exemple-type: la grille étudiée hier). Je pense que ça peut être l'occasion pour lui de développer de très beaux traits de caractère: concentration, courage, persévérance, humilité.
Prions.
Euh, je m'égare...
Rappelez-vous le prétendu proverbe chinois qui dit qu'il est difficile d'attraper un chat noir dans une pièce sombre, surtout quand il n'y est pas. C'est toute la problématique des "cinq et huit"; ça peut vous faire une raison de les fuir comme la peste, mais pour ma part c'est la raison pour laquelle je les préfère à tout autre problème (quand on trouve une solution à pentagone final sur une grille qui a longtemps paru insoluble, c'est particulièrement jouissif).
Toujours est-il que quand je vous dis qu'on peut pas terminer une grille sur cinq cases, faites pas chier, ça veut dire qu'on peut pas, voilà, trust me on that.
Mais vous l'aurez remarqué, dans mon inventaire, je vous dis juste "cinq ou huit", pas "on peut terminer sur cinq" ni "on doit terminer sur huit". C'est mon côté un peu sado-masochiste. Hin hin hin.
(1) Il s'agit bien sûr de latin "macaronique", violemment incorrect et je vous prie de m'en excuser. La vraie locution proverbiale, inspirée d'Aristote, est primum vivere, deinde philosophari: d'abord vivre, ensuite philosopher. Notez que c'est philosophari et non philosophare, parce qu'il s'agit d'un verbe déponent (déponent, pas déconnant), c'est-à-dire "de forme passive et de sens actif". Monsieur mon vénérable père, qui est agrégé de latin (ça vous en bouche un coin, hein?), me suggère "primum solutionem invenire, deinde philosophari", ou mieux "primum concludere, deinde philosophari"... mais c'est tellement plus clair en mauvais latin.
Ainsi s'achève la minute pédante de Petitagore.
Ça ne nous dispense quand même pas de tout effort de réflexion. Qu'est-ce qui peut représenter un ensemble de huit cases prenables en un seul coup final? En général, le plus simple est un couloir de huit cases qui traverse le tore de part en part, mais pas de pot, sur cette grille, on ne peut pas en trouver un. En revanche, il y a un octogone (un seul), même s'il ne se voit pas beaucoup, réparti qu'il est sur les côtés gauche et droit du tore: 24, 32, 38, 37 sur le côté gauche, 31, 36, 44, 45 sur le côté droit. L'octogone, ce sera le dernier coup de la partie, mais l'avant-dernier coup de la partie, ce sera classiquement un pentagone marié à cet octogone par deux cases... c'est-à-dire les cases 28, 29 et 30 (que nous prendrons par un coup gagnant jaune) ainsi que 36 et 31 (qui seront prises en bleu au coup final, en même temps que l'ensemble de l'octogone).
Nous en savons assez, à l'attaque!
Voici ma solution à moi, et elle a bien dû me demander quarante secondes de tâtonnements: 43 26 35 40 18 3 10 12 6 15 23 21 1 29 32.
Mon solveur peut vous en suggérer plein d'autres, toutes plus inélégantes les unes que les autres, correspondant à ces affreux cavexes à mortaise, non inversibles (reportez-vous aux épisodes précédents):
- C'est trop affreux, je ne veux pas voir ça...:
- Avec le cavexe à mortaise 0: 14 39 4 42 6 27 20 12 10 18 23 22 7 29 44.
Avec le cavexe à mortaise 1: 43 15 13 19 41 27 18 34 30 23 6 9 2 1 32.
Avec le cavexe à mortaise 2: 34 13 41 2 11 26 28 33 8 22 29 14 6 0 36.
Avec le cavexe à mortaise 3: 15 35 29 26 13 43 3 40 10 21 25 9 30 7 37.
Avec le cavexe à mortaise 4: 2 19 11 25 34 39 41 28 5 8 29 21 1 22 44.
Avec le cavexe à mortaise 5: 0 22 16 17 11 3 13 40 33 27 20 7 42 28 31.
Avec le cavexe à mortaise 6: 22 25 17 10 0 3 13 20 40 33 14 7 35 30 31.
Vous exigez une solution élégante, avec un beau cavexe rondouillard? Oh, écoutez, ça me gonfle de vous expliquer, c'est trop simple. Je vous donne juste la photo du cavexe, débrouillez-vous:
- Allez, je vous explique quand même...:
- 22 7 16 1 17 3 14 25 13 19 (hors du cavexe), 34 40 42 29 36 (dedans).
Donc, on est d'accord, terminer en sacrifiant huit cases, c'est vraiment très facile (du moins dans la plupart des cas) -- beaucoup plus facile, en tout cas, que de terminer sur un pentagone. Rappelez-vous quelle galère ça a été sur la grille d'hier.
-- Ben pourquoi ne pas toujours terminer sur huit cases, alors?
-- Parce que le but du jeu est de trouver l'optimum de cases jaunes, pas un optimum au rabais. Terminer sur huit quand on peut terminer sur cinq, c'est déchoir, mon cher fils.
-- Ben pourquoi vous terminez pas sur cinq ce coup-ci, alors?
-- Parce que ça n'est pas possible.
-- Et qu'est-ce que vous en savez?
-- Je le sais parce que mon solveur a essayé et n'y est pas parvenu.
-- Et qui vous dit que votre solveur n'est pas truffé de bugs? C'est vous qui l'avez écrit et, hum, sans vouloir vous vexer, mon cher maître, vous avez déjà eu l'humilité de reconnaître que vous n'êtes point infaillible.
-- Je ne suis peut-être pas infaillible en toutes circonstances, mais je vous le déclare bien haut, ex cathedra, du haut de ma chaire pontificale triancesque, on ne peut pas atteindre l'optimum de la grille "prof" en terminant sur un pentagone.
-- Je déteste les énoncés dogmatiques. On ne peut pas because?
-- Because c'est comme ça et je le sais.
-- Et si vous vous trompiez, cher maître? Car après tout, la grille "prof" comporte bien deux pentagones mariés -- contrairement à la grille "mai" que vous aviez cette fois légitimement, j'en conviens volontiers, terminé en sacrifiant huit cases.
-- Mais tu les vois où, tes pentagones mariés, petit connard?
-- Ici, cher maître. Premier pentagone 28, 29, 30, 31, 36; second pentagone 30, 31... 22, 23, 24.
-- Ah. En effet.
Eh bien oui, c'est ça le problème avec les "cinq ou huit": on n'a pas toujours à sa disposition de preuve mathématique démontrant l'impossibilité absolue de terminer en ne sacrifiant que cinq cases. Mon solveur me fournit des preuves informatiques, mais moi non plus elles ne me satisfont pas complètement, et moi aussi j'ai un tempérament qui m'incite à demander... la preuve de la preuve.
Alors je vais essayer. Regardez ci-dessus les deux pentagones mariés, correspondant aux deux derniers coups de la partie, et demandez-vous quel pourrait être l'antépénultième coup de la partie qui pourrait être joué avant la prise de ce coacervat final. Ce coup antépénultième ne prendrait donc, par hypothèse, que trois cases (sans quoi ça ne serait pas un coup gagnant). Or on peut faire valoir qu'aucun des polygones mariés par deux cases à ce coacervat final (par exemple l'heptagone 20, 19, 26, 27, 35, plus les deux cases 28 et 29 déjà dans le coacervat) n'est un pentagone. Ce n'est pas une preuve formelle, mais c'est un indice fort.
-- Mais l'antépénultième coup pourrait peut-être comporter une case isolée tenon-mortaise (note au lecteur: reportez-vous aux épisodes précédents) dans un hexagone marié avec le coacervat final, et par conséquent on pourrait quand même prendre trois cases en un coup.
-- Euh... Ce n'est peut-être pas inconcevable, mais ça me paraît quand même bien douteux. Et de toute façon, mon solveur dit que ça n'est pas possible sur cette grille.
-- Ou encore l'antépénultième coup pourrait prendre un petit couloir de trois cases.
-- Mmmmouiii... peut-être, en effet.
-- Mais pas en l'occurrence?
-- Il me semble que non.
-- Pourquoi?
-- Parce qu'il y a trop de cases dans la largeur de cette grille, qui est assez dense. Et par ailleurs, parce que mon solveur le dit.
-- Ça ne me convainc pas.
-- Homme de peu de foi...
Bon. Je crois qu'on n'en sortira pas.
L'honnêteté me force à dire que c'est peut-être là une faiblesse de mon jeu, en tout cas ce n'est pas conforme à la règle esthétique que je m'étais fixée: que l'optimum d'une grille puisse être déterminé sans erreur et sans peine. Cette faiblesse disparaîtrait peut-être en pratique si je diffusais le listing de mon solveur et le laissais vérifier par plein d'informaticiens compétents -- mais là encore, l'honnêteté me force à admettre que je l'ai écrit avec des techniques très inélégantes, que j'ai honte de montrer à quel point je m'y suis pris comme un manche; il faudrait que je trouve le courage de le réécrire proprement... mais ça me gonfle parce que tout moche qu'il est il m'a l'air de marcher très bien. J'applique donc l'adage informatique: if it ain't broke, don't fix it.
D'un autre côté, cette incertitude sur les quelques rares grilles "cinq ou huit" représente peut-être un avantage pour moi, car elle rend mon autorité pontificale absolument indispensable. Appelez-moi Eminence (non, pas Votre Sainteté, faut pas déconner quand même).
Mais c'est peut-être surtout -- et c'est en tout cas ainsi que je préfère le voir -- une école de vertu pour le joueur de ce casse-tête, qui peut certes se montrer très "fort contre la logique", mais ne peut quand même pas aller jusqu'à se prétendre "aussi fort que la logique". Cela met donc à sa disposition un exercice non pas seulement intellectuel, mais également moral, en lui demandant de temps à autre de chercher courageusement une solution qui n'existe peut-être pas, faute de quoi il risque de baisser les bras alors que la solution existait et pouvait être trouvée (exemple-type: la grille étudiée hier). Je pense que ça peut être l'occasion pour lui de développer de très beaux traits de caractère: concentration, courage, persévérance, humilité.
Prions.
Euh, je m'égare...
Rappelez-vous le prétendu proverbe chinois qui dit qu'il est difficile d'attraper un chat noir dans une pièce sombre, surtout quand il n'y est pas. C'est toute la problématique des "cinq et huit"; ça peut vous faire une raison de les fuir comme la peste, mais pour ma part c'est la raison pour laquelle je les préfère à tout autre problème (quand on trouve une solution à pentagone final sur une grille qui a longtemps paru insoluble, c'est particulièrement jouissif).
Toujours est-il que quand je vous dis qu'on peut pas terminer une grille sur cinq cases, faites pas chier, ça veut dire qu'on peut pas, voilà, trust me on that.
Mais vous l'aurez remarqué, dans mon inventaire, je vous dis juste "cinq ou huit", pas "on peut terminer sur cinq" ni "on doit terminer sur huit". C'est mon côté un peu sado-masochiste. Hin hin hin.
(1) Il s'agit bien sûr de latin "macaronique", violemment incorrect et je vous prie de m'en excuser. La vraie locution proverbiale, inspirée d'Aristote, est primum vivere, deinde philosophari: d'abord vivre, ensuite philosopher. Notez que c'est philosophari et non philosophare, parce qu'il s'agit d'un verbe déponent (déponent, pas déconnant), c'est-à-dire "de forme passive et de sens actif". Monsieur mon vénérable père, qui est agrégé de latin (ça vous en bouche un coin, hein?), me suggère "primum solutionem invenire, deinde philosophari", ou mieux "primum concludere, deinde philosophari"... mais c'est tellement plus clair en mauvais latin.
Ainsi s'achève la minute pédante de Petitagore.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Ven 27 Mar 2015 - 9:46
Bien! Je crois vous avoir assez sorti de la routine au cours des derniers jours, je reprends donc l'étude méthodique des grilles de difficulté moyenne de mon inventaire, et nous en sommes maintenant à la grille "grincheux":
Je ne lui vois rien de particulier jusqu'ici, et elle me paraît tout à fait soluble avec discipline et méthode.
Je ne lui vois rien de particulier jusqu'ici, et elle me paraît tout à fait soluble avec discipline et méthode.
- Point de départ du raisonnement:
- C'est une grille de 38 cases, donc si on en sacrifie deux (bleues) au départ comme il est presque toujours nécessaire, il en restera 36, qui est un multiple de 3. Donc il faut terminer sur un polygone convexe dont le nombre de cases soit lui-même un multiple de 3, c'est-à-dire un hexagone. Et comme le dernier coup d'une partie à score optimal classique est toujours joué sur un pentagone (vous trouverez le théorème de l'avant-dernier coup dans ce post, avec un bel intertitre de couleur), nous cherchons donc sur la grille un hexagone marié à un pentagone.
Pour ceux qui prennent le film en cours de projection, c'est dans ce post que j'ai introduit la notion de cavexe.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Ven 27 Mar 2015 - 12:24
Après examen approfondi par mon solveur, il semble que la grille "grincheux" soit assez pauvre en cavexes rondouillards -- mais ça n'est pas très grave car elle peut quand même en accueillir un qui me paraît académique en diable:
Par discipline personnelle et intégrité intellectuelle, je m'astreins toujours à chercher (et généralement, à trouver) une solution par mes propres moyens avant de demander à mon solveur de bosser. L'honnêteté me force à dire que je n'avais pas vu le très beau cavexe ci-dessus, mais seulement le premier de ceux représentés ci-dessous:
Il est vrai que celui que j'ai trouvé n'était pas trop difficile à photographier mentalement, contrairement aux deux derniers ci-dessus.
Je vous engage vivement à essayer de reconstituer ces cavexes vous-mêmes avant d'attaquer une résolution avec celui d'entre eux qui vous plaira le plus: c'est un excellent entraînement.
Solutions complètes en fin de journée.
Par discipline personnelle et intégrité intellectuelle, je m'astreins toujours à chercher (et généralement, à trouver) une solution par mes propres moyens avant de demander à mon solveur de bosser. L'honnêteté me force à dire que je n'avais pas vu le très beau cavexe ci-dessus, mais seulement le premier de ceux représentés ci-dessous:
Il est vrai que celui que j'ai trouvé n'était pas trop difficile à photographier mentalement, contrairement aux deux derniers ci-dessus.
Je vous engage vivement à essayer de reconstituer ces cavexes vous-mêmes avant d'attaquer une résolution avec celui d'entre eux qui vous plaira le plus: c'est un excellent entraînement.
Solutions complètes en fin de journée.
Dernière édition par Petitagore le Ven 27 Mar 2015 - 14:14, édité 1 fois (Raison : un mot pour un autre)
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Ven 27 Mar 2015 - 19:07
Allons-y pour la résolution de la grille "grincheux". A titre pédagogique (pour les débutants), avant de donner la solution complète, j'indique comment on peut dessiner les cavexes.
Dessinons le cavexe le plus concis: 22 30 23 28 (bleu), 26 8 (jaune). Elémentaire... mais efficace!
Dessinons le cavexe 1 (qui est celui qu'a identifié mon petit cerveau, et qu'on peut donc considérer comme une solution humainement accessible sans capacités de clairvoyance particulières): 32 35 25 34 (bleu), 5 31 36 (jaune).
Dessinons le cavexe 2 (massif mais facile à photographier mentalement): 21 22 16 28 (bleu), 36 25 14 4 (jaune).
Dessinons le cavexe 3: 32 35 25 34 (bleu), 5 31 13 17 10. On peut s'arrêter là (c'est ce qu'a fait mon solveur), mais il est très tentant d'"arrondir les angles" en cliquant encore sur 6.
Enfin, dessinons le cavexe 4: 6 3 2 7 (bleu), 33 37 25 36 (jaune). Honnêtement, je trouve que c'est une idée un peu tordue... mais c'est comme ça que travaille le solveur.
Et je vous souhaite une bonne soirée!
Dessinons le cavexe le plus concis: 22 30 23 28 (bleu), 26 8 (jaune). Elémentaire... mais efficace!
- Solution complète avec le cavexe concis:
- 13 11 7 2 21 35 5 37 19 10 (hors du cavexe), 8 27 30 (dedans).
Dessinons le cavexe 1 (qui est celui qu'a identifié mon petit cerveau, et qu'on peut donc considérer comme une solution humainement accessible sans capacités de clairvoyance particulières): 32 35 25 34 (bleu), 5 31 36 (jaune).
- Solution complète avec le cavexe 1:
- 20 22 27 7 19 11 17 2 8 (hors du cavexe), 36 31 5 25 (dedans).
Dessinons le cavexe 2 (massif mais facile à photographier mentalement): 21 22 16 28 (bleu), 36 25 14 4 (jaune).
- Solution complète avec le cavexe 2:
- 9 34 0 30 18 17 19 2 (hors du cavexe), 4 13 35 36 16 (dedans).
Dessinons le cavexe 3: 32 35 25 34 (bleu), 5 31 13 17 10. On peut s'arrêter là (c'est ce qu'a fait mon solveur), mais il est très tentant d'"arrondir les angles" en cliquant encore sur 6.
- Solution complète avec le cavexe 3:
- 36 15 8 14 1 28 21 (hors du cavexe), 10 12 19 18 0 35 (dedans). Ou encore, avec le cavexe "amélioré": 2 21 7 8 28 36 (hors du cavexe), 6 10 17 13 31 5 25 (dedans).
Enfin, dessinons le cavexe 4: 6 3 2 7 (bleu), 33 37 25 36 (jaune). Honnêtement, je trouve que c'est une idée un peu tordue... mais c'est comme ça que travaille le solveur.
- Solution complète avec le cavexe 4:
- 20 12 18 23 9 16 29 27 (hors du cavexe), 36 24 32 33 3 (dedans).
Et je vous souhaite une bonne soirée!
Dernière édition par Petitagore le Ven 27 Mar 2015 - 19:49, édité 1 fois (Raison : Amélioration du commentaire sur le cavexe 3.)
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Sam 28 Mar 2015 - 10:28
Je continue avec les grilles supposées de difficulté moyenne dans mon inventaire, et le problème du jour est donc la résolution de la grille "joyeux".
Le plus pédagogique serait peut-être que je vous laisse vous dépétrer tous seuls au moins un moment, mais je ne peux pas m'empêcher de vous donner un gros indice...
Le plus pédagogique serait peut-être que je vous laisse vous dépétrer tous seuls au moins un moment, mais je ne peux pas m'empêcher de vous donner un gros indice...
- Ne lisez pas si vous savez déjà résoudre une grille....:
- La solution du jour sera très similaire à ce que nous avons déjà vu en étudiant la grille "mai".
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Sam 28 Mar 2015 - 18:13
J'ai un tempérament mathématico-mystique en même temps que taquin, j'ai déjà dû vous donner l'occasion de vous en apercevoir. Eh bien, la résolution de la grille "joyeux" va une fois de plus donner à ce tempérament bizarre l'occasion de s'exprimer, je ne sais pas si vous aurez lieu de vous en réjouir mais au moins vous en aurai-je prévenus.
Commençons par envisager les choses, très classiquement, en termes logiques et même arithmétiques.
La grille "joyeux" comporte 40 cases. Si nous en sacrifions deux (bleues) au départ comme il est presque toujours nécessaire, il nous en reste 38, c'est-à-dire un multiple de trois majoré de deux. Par conséquent, la fin d'une résolution optimale de cette grille entraînera le sacrifice d'un nombre de cases bleues qui sera lui aussi un multiple de trois majoré de deux.
L'idéal théorique serait de terminer en jouant le dernier coup sur un pentagone (5 = 3 * 1 + 2), un pis-aller de sacrifier en fin de partie non pas cinq mais huit cases (8 = 3 * 2 + 2). Eh bien, avec cette grille "joyeux", nous nous trouvons dans le même cas de figure que naguère avec la grille "mai" qui comptait d'ailleurs elle aussi quarante cases: nous pouvons assurer qu'il est impossible de terminer sur un pentagone en vertu du théorème de l'avant-dernier coup, lequel exige que le dernier coup soit lui aussi joué sur un pentagone. Or ni la grille "joyeux" ni la grille "mai" ne possèdent nulle part un couple de pentagones mariés. Rabaissons donc nos ambitions, et terminons en sacrifiant huit cases bleues et non pas seulement cinq.
Soit dit en passant, ni la grille "joyeux" ni la grille "mai" ne méritent pour cela d'entrer dans la catégorie bizarre des grilles que j'appelle "cinq ou huit", celles dont le score optimal est impossible à déterminer a priori. Les éléments de réflexion sont certes les mêmes que pour ces grilles maudites, mais ici, point d'ambiguïté: il faut terminer en sacrifiant huit cases, point final.
Et par conséquent, ça devrait être assez simple. Comme j'ai déjà eu récomment l'occasion de vous le dire, si l'on est certain qu'on terminera la résolution de la grille en sacrifiant l'impressionnante quantité de huit cases, alors on peut anticiper une belle abondance de solutions: on peut sans doute terminer sur un couloir de huit cases, sur un octogone, sur deux quadrilatères ou encore (et tant pis si c'est moche) sur un hexagone marié à un quadrilatère (c'est-à-dire 6 cases, plus 4 cases, mais aussi moins 2 cases qu'il ne faut pas compter deux fois car hexagone et quadrilatère devront se les partager; 6 + 4 - 2 = 8 ).
Mon tempérament de soudard m'incite à vous répéter cette obscénité: quand on doit terminer en sacrifiant huit cases, alors il faut attaquer la grille avec "sa bite et son couteau": dessiner un cavexe est alors généralement superflu, cela marque plus un manque de confiance en soi qu'une saine prudence. "Faites péter vos galons", aurait dit mon capitaine: vous êtes des zèbres, cornegidouille, vous avez déjà résolu des dizaines de grilles (ah non? pas vous? ben moi si), vous n'allez quand même pas vous laisser emmpistrouiller par une idiote de grille pour débutants.
Sur la grille "joyeux" qui nous occupe aujourd'hui, ce n'est que partiellement vrai. Mais tant pis, à l'attaque.
Allez, commençons par le plus simple: prévoyons de terminer sur un couloir de huit cases. Il doit y en avoir plein...
Euh...
Bon, d'accord, il n'y en a que deux. On peut même dire que ce sont deux variantes du même, mais peu importe, c'est suffisant.
Et je le prouve, nom de Guieu!
Je vous avais bien dit que c'était de la gnognotte. Allez, on continue, on trouve un moyen de terminer sur un octogone, en avant!
Euh...
Tiens, c'est bizarre, c'est plus difficile que prévu.
Carrément plus difficile, même...
Ah ouais, OK. Bon, d'accord, autant pour moi, non, on ne peut pas terminer sur le seul octogone de la grille (coupé en deux morceaux de part et d'autre du tore: 0, 10, 15, 14 à gauche, 9, 13, 19 20 à droite). Pourquoi? Ben tout bêtement, encore et toujours, à cause de ce satané théorème de l'avant-dernier coup: il faudrait que cet octogone fût marié à un pentagone... or pas de pot, les huit polygones avec lesquels cet octogone est marié sont deux quadrilatères, quatre hexagones et deux heptagones, mais zéro pentagone. C'est vraiment pas de chance.
Bon, franchement, je commence à me sentir un peu ridicule avec ma bite et mon couteau, permettez-moi donc de les remiser en ma culotte, de me draper derechef dans ma dignité et d'en revenir à des solutions plus académiques.
Or donc, où en étions-nous? Ah oui, on doit pouvoir terminer sur deux quadrilatères, non?
Euh...
Je vais vous faire un aveu: les solutions à deux quadrilatères, c'est presque toujours le solveur qui les trouve parce que, franchement, c'est trop fort pour moi. Je lui cède donc la parole:
OK, c'est pas moi qui ai trouvé cette solution, mais je ne vous mentais pas en vous disant que c'était possible, et c'est quand même le principal.
Je vous ai aussi dit qu'il était possible de terminer sur un hexagone marié à un quadrilatère. Justement, nous venons de repérer deux quadrilatères sur la grille... Mmmoui, on peut dessiner de bons cavexes avec:
Et ça va nous donner de jolies solutions presque orthodoxes:
Eh bien voilà voilà, je crois qu'on a fait le tour...
-- Non.
Comment ça, non? Qui parle, d'abord?
-- Moi. Je suis ton solveur, et je représente ici l'omniscience de la Mathématique. Prosterne-toi, ô mortel, car je t'ai été envoyé pour te révéler la sagesse du Très-Haut.
Tu déconnes.
-- Que non pas, vile créature! Et comme par ma bouche c'est la Logique en personne qui va parler, je t'intime et te commande de commencer par lui témoigner le plus vif respect en entamant un nouveau post tout exprès. Et tout de suite encore!
Ah ben d'accord chef, à vos ordres chef. Je termine donc ce post ici, et j'en entame tout de suite un autre.
-- Plus vite que ça!
Oui chef. Excusez-moi chef.
Commençons par envisager les choses, très classiquement, en termes logiques et même arithmétiques.
La grille "joyeux" comporte 40 cases. Si nous en sacrifions deux (bleues) au départ comme il est presque toujours nécessaire, il nous en reste 38, c'est-à-dire un multiple de trois majoré de deux. Par conséquent, la fin d'une résolution optimale de cette grille entraînera le sacrifice d'un nombre de cases bleues qui sera lui aussi un multiple de trois majoré de deux.
L'idéal théorique serait de terminer en jouant le dernier coup sur un pentagone (5 = 3 * 1 + 2), un pis-aller de sacrifier en fin de partie non pas cinq mais huit cases (8 = 3 * 2 + 2). Eh bien, avec cette grille "joyeux", nous nous trouvons dans le même cas de figure que naguère avec la grille "mai" qui comptait d'ailleurs elle aussi quarante cases: nous pouvons assurer qu'il est impossible de terminer sur un pentagone en vertu du théorème de l'avant-dernier coup, lequel exige que le dernier coup soit lui aussi joué sur un pentagone. Or ni la grille "joyeux" ni la grille "mai" ne possèdent nulle part un couple de pentagones mariés. Rabaissons donc nos ambitions, et terminons en sacrifiant huit cases bleues et non pas seulement cinq.
Soit dit en passant, ni la grille "joyeux" ni la grille "mai" ne méritent pour cela d'entrer dans la catégorie bizarre des grilles que j'appelle "cinq ou huit", celles dont le score optimal est impossible à déterminer a priori. Les éléments de réflexion sont certes les mêmes que pour ces grilles maudites, mais ici, point d'ambiguïté: il faut terminer en sacrifiant huit cases, point final.
Et par conséquent, ça devrait être assez simple. Comme j'ai déjà eu récomment l'occasion de vous le dire, si l'on est certain qu'on terminera la résolution de la grille en sacrifiant l'impressionnante quantité de huit cases, alors on peut anticiper une belle abondance de solutions: on peut sans doute terminer sur un couloir de huit cases, sur un octogone, sur deux quadrilatères ou encore (et tant pis si c'est moche) sur un hexagone marié à un quadrilatère (c'est-à-dire 6 cases, plus 4 cases, mais aussi moins 2 cases qu'il ne faut pas compter deux fois car hexagone et quadrilatère devront se les partager; 6 + 4 - 2 = 8 ).
Mon tempérament de soudard m'incite à vous répéter cette obscénité: quand on doit terminer en sacrifiant huit cases, alors il faut attaquer la grille avec "sa bite et son couteau": dessiner un cavexe est alors généralement superflu, cela marque plus un manque de confiance en soi qu'une saine prudence. "Faites péter vos galons", aurait dit mon capitaine: vous êtes des zèbres, cornegidouille, vous avez déjà résolu des dizaines de grilles (ah non? pas vous? ben moi si), vous n'allez quand même pas vous laisser emmpistrouiller par une idiote de grille pour débutants.
Sur la grille "joyeux" qui nous occupe aujourd'hui, ce n'est que partiellement vrai. Mais tant pis, à l'attaque.
Allez, commençons par le plus simple: prévoyons de terminer sur un couloir de huit cases. Il doit y en avoir plein...
Euh...
Bon, d'accord, il n'y en a que deux. On peut même dire que ce sont deux variantes du même, mais peu importe, c'est suffisant.
Et je le prouve, nom de Guieu!
- Solutions complètes avec couloirs:
- Avec le couloir 0 (solution trouvée par mon petit cerveau): 3 14 10 9 29 19 21 7 34 17 25 33 16.
Avec le couloir 1: 35 28 22 34 7 0 12 19 10 37 25 24 30.
Je vous avais bien dit que c'était de la gnognotte. Allez, on continue, on trouve un moyen de terminer sur un octogone, en avant!
Euh...
Tiens, c'est bizarre, c'est plus difficile que prévu.
Carrément plus difficile, même...
Ah ouais, OK. Bon, d'accord, autant pour moi, non, on ne peut pas terminer sur le seul octogone de la grille (coupé en deux morceaux de part et d'autre du tore: 0, 10, 15, 14 à gauche, 9, 13, 19 20 à droite). Pourquoi? Ben tout bêtement, encore et toujours, à cause de ce satané théorème de l'avant-dernier coup: il faudrait que cet octogone fût marié à un pentagone... or pas de pot, les huit polygones avec lesquels cet octogone est marié sont deux quadrilatères, quatre hexagones et deux heptagones, mais zéro pentagone. C'est vraiment pas de chance.
Bon, franchement, je commence à me sentir un peu ridicule avec ma bite et mon couteau, permettez-moi donc de les remiser en ma culotte, de me draper derechef dans ma dignité et d'en revenir à des solutions plus académiques.
Or donc, où en étions-nous? Ah oui, on doit pouvoir terminer sur deux quadrilatères, non?
Euh...
Je vais vous faire un aveu: les solutions à deux quadrilatères, c'est presque toujours le solveur qui les trouve parce que, franchement, c'est trop fort pour moi. Je lui cède donc la parole:
- Solution avec deux quadrilatères:
- 37 23 36 29 4 15 18 38 6 34 27 19 0 14
OK, c'est pas moi qui ai trouvé cette solution, mais je ne vous mentais pas en vous disant que c'était possible, et c'est quand même le principal.
Je vous ai aussi dit qu'il était possible de terminer sur un hexagone marié à un quadrilatère. Justement, nous venons de repérer deux quadrilatères sur la grille... Mmmoui, on peut dessiner de bons cavexes avec:
Et ça va nous donner de jolies solutions presque orthodoxes:
- Solutions avec un hexagone marié à un quadrilatère:
- Avec le cavexe 0: 10 37 1 4 30 16 12 38 8 29 (hors du cavexe) 31 18 28 (dedans).
Avec le cavexe 1: 34 30 32 6 29 23 1 2 9 (hors du cavexe), 15 13 24 28 (dedans).
Avec le cavexe 2: 2 16 4 35 0 22 8 (hors du cavexe), 6 17 30 34 24 20 (dedans).
Eh bien voilà voilà, je crois qu'on a fait le tour...
-- Non.
Comment ça, non? Qui parle, d'abord?
-- Moi. Je suis ton solveur, et je représente ici l'omniscience de la Mathématique. Prosterne-toi, ô mortel, car je t'ai été envoyé pour te révéler la sagesse du Très-Haut.
Tu déconnes.
-- Que non pas, vile créature! Et comme par ma bouche c'est la Logique en personne qui va parler, je t'intime et te commande de commencer par lui témoigner le plus vif respect en entamant un nouveau post tout exprès. Et tout de suite encore!
Ah ben d'accord chef, à vos ordres chef. Je termine donc ce post ici, et j'en entame tout de suite un autre.
-- Plus vite que ça!
Oui chef. Excusez-moi chef.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Invité Sam 28 Mar 2015 - 19:12
Tout en "un"... ^^
Maths, littérature, et humour... Tout est unifié, "un", ...
Mais non, rétorque Lucy (Luc Besson), c'est une erreur de croire que "un" est un.
(référence cinématographique, et biologique, mais pas que...)
Ah mais alors, si un n'est pas un, comment on va résoudre ici en comptant alors, nom d'une schtroumphette. ^^
Ah, mais ça m'explique du coup l'hexagone à un nombre étrange de côtés donc, j'ai tout compris. Nous avons changé de dimension.
C'est pire que "Le livre qui rend fou".
Invité- Invité
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Dim 29 Mar 2015 - 18:41
Kara Magic whale, merci de tes encouragements.
Eh bien non, en effet, nous n'avons pas encore totalement fait le tour des solutions de la grille "joyeux": mon solveur a aussi trouvé dessus des solutions qui me paraissent... complètement extra-terrestres, d'une logique totalement siphonnée digne des Shadoks ("pourquoi faire simple quand on peut faire compliqué?") mais que j'hésite quand même fortement à qualifier de stupides; bien au contraire, je trouve ça tellement sidérant que je serais plutôt tenté de crier au génie. En tout cas, ces solutions me laissent vraiment pantois. Je n'avais jamais vu des trucs pareils... et surtout il ne me serait jamais venu à l'idée de les chercher.
Il faut dire que mon solveur n'utilise pas ses yeux pour trouver l'optimum d'une grille... pour la raison fort simple qu'il n'en a pas. Il ne tient donc aucun compte des notions de gauche, de droite, de haut, de bas, de bords, de coins, de couloirs: il n'a pas la moindre idée de l'emplacement ni même de l'existence des sommets des cases triangulaires. Tout ce qu'il sait, c'est qu'autour d'une case numérotée n, il y a trois autres cases numérotées o, p et q. Qui plus est, pour le forcer à envisager les possibilités les plus bizarres, je lui chamboule (avec un algorithme pseudo-aléatoire) la numérotation de ces cases chaque fois que je lui demande de trouver une solution optimale (c'est de cette façon que je le rends inventif et créatif). La conséquence en est que quand moi j'ai le sentiment qu'une solution s'impose tellement elle est visible comme le nez au milieu de la figure (par exemple, dans le cas qui nous occupe, je pense aux solutions qui ont recours à un couloir de huit cases), lui ne la voit pas et continue à chercher dans le noir complet un moyen de se dépatouiller avec ces listes de voisins, seuls éléments de réflexion dont il dispose.
Eh bien, comprend qui peut, mais dans à peu près les trois quarts des cas, et à ma profonde stupéfaction, quand je lui donne à résoudre cette grille "joyeux", au lieu de retrouver l'une des solutions claires, logiques et élégantes que nous avons vues hier... il préfère terminer la résolution de la grille avec l'un de ces trois coacervats:
Tous trois laissent onze cases libres, et systématiquement le même sous-ensemble composé d'un quadrilatère et d'un pentagone mariés par deux cases. L'espace encore vide compte aussi un dernier polygone, qui est un heptagone ou un hexagone.
La colossale finesse du solveur, c'est de se débrouiller pour que, dans les trois coups qu'il va falloir jouer dans cet ensemble pour terminer la partie, il y ait un coup gagnant entre deux coups perdants. Il va donc prendre:
- une case, puis trois, puis sept;
- ou deux, puis trois, puis six;
- ou quatre, puis trois, puis quatre.
Essayez, vous verrez qu'en effet c'est possible -- mais pétard ne me dites pas que ça n'est pas une idée complètement tordue!
Eh bien, visiblement, du point de vue de mon solveur, ce sont là les solutions simples qui tombent sous le sens, au point qu'il les préfère dans les trois quarts des cas.
Je soupçonne qu'il y a là derrière quelque vérité mathématique dont la simplicité m'échappe totalement.
Bon. Je vous laisse un peu gamberger sur cette question, et je reviendrai pour vous parler des émois mystiques que cela m'inspire.
Eh bien non, en effet, nous n'avons pas encore totalement fait le tour des solutions de la grille "joyeux": mon solveur a aussi trouvé dessus des solutions qui me paraissent... complètement extra-terrestres, d'une logique totalement siphonnée digne des Shadoks ("pourquoi faire simple quand on peut faire compliqué?") mais que j'hésite quand même fortement à qualifier de stupides; bien au contraire, je trouve ça tellement sidérant que je serais plutôt tenté de crier au génie. En tout cas, ces solutions me laissent vraiment pantois. Je n'avais jamais vu des trucs pareils... et surtout il ne me serait jamais venu à l'idée de les chercher.
Il faut dire que mon solveur n'utilise pas ses yeux pour trouver l'optimum d'une grille... pour la raison fort simple qu'il n'en a pas. Il ne tient donc aucun compte des notions de gauche, de droite, de haut, de bas, de bords, de coins, de couloirs: il n'a pas la moindre idée de l'emplacement ni même de l'existence des sommets des cases triangulaires. Tout ce qu'il sait, c'est qu'autour d'une case numérotée n, il y a trois autres cases numérotées o, p et q. Qui plus est, pour le forcer à envisager les possibilités les plus bizarres, je lui chamboule (avec un algorithme pseudo-aléatoire) la numérotation de ces cases chaque fois que je lui demande de trouver une solution optimale (c'est de cette façon que je le rends inventif et créatif). La conséquence en est que quand moi j'ai le sentiment qu'une solution s'impose tellement elle est visible comme le nez au milieu de la figure (par exemple, dans le cas qui nous occupe, je pense aux solutions qui ont recours à un couloir de huit cases), lui ne la voit pas et continue à chercher dans le noir complet un moyen de se dépatouiller avec ces listes de voisins, seuls éléments de réflexion dont il dispose.
Eh bien, comprend qui peut, mais dans à peu près les trois quarts des cas, et à ma profonde stupéfaction, quand je lui donne à résoudre cette grille "joyeux", au lieu de retrouver l'une des solutions claires, logiques et élégantes que nous avons vues hier... il préfère terminer la résolution de la grille avec l'un de ces trois coacervats:
- Si vous voulez essayer vous-mêmes...:
- ... voici comment construire les trois coacervats:
Coacervat 0: 4 18 16 6 31 19 14 22 27 30 38.
Coacervat 1: 14 7 28 34 9 33 13 31 22 12 15.
Coacervat 2: 26 38 28 24 30 6 14 18 13 8 23.
Tous trois laissent onze cases libres, et systématiquement le même sous-ensemble composé d'un quadrilatère et d'un pentagone mariés par deux cases. L'espace encore vide compte aussi un dernier polygone, qui est un heptagone ou un hexagone.
La colossale finesse du solveur, c'est de se débrouiller pour que, dans les trois coups qu'il va falloir jouer dans cet ensemble pour terminer la partie, il y ait un coup gagnant entre deux coups perdants. Il va donc prendre:
- une case, puis trois, puis sept;
- ou deux, puis trois, puis six;
- ou quatre, puis trois, puis quatre.
Essayez, vous verrez qu'en effet c'est possible -- mais pétard ne me dites pas que ça n'est pas une idée complètement tordue!
- Je vous montre, mais essayez donc vous-mêmes:
- Avec le coacervat 0 (construit par 4 18 16 6 31 19 14 22 27 30 38), on peut encore jouer un coup gagnant en cliquant 10, puis 3, puis 1 (prise d'une case, puis de trois, puis de sept), ou 39, puis 36, puis 2 (prise de quatre cases, puis de trois, puis de quatre).
Avec le coacervat 1 (construit par 14 7 28 34 9 33 13 31 22 12 15), vous pouvez jouer 0, puis 2, puis 4 (prise de deux cases , puis trois, puis six), ou 37, puis 36, puis 2 (prise de quatre cases, puis trois, puis quatre).
Avec le coacervat 2 (construit par 26 38 28 24 30 6 14 18 13 8 23), vous pouvez jouer 0, puis 35, puis 3 (prise d'une case, puis trois, puis sept), ou 16, puis 36, puis 2 (prise de quatre cases, puis trois, puis quatre).
Eh bien, visiblement, du point de vue de mon solveur, ce sont là les solutions simples qui tombent sous le sens, au point qu'il les préfère dans les trois quarts des cas.
Je soupçonne qu'il y a là derrière quelque vérité mathématique dont la simplicité m'échappe totalement.
Bon. Je vous laisse un peu gamberger sur cette question, et je reviendrai pour vous parler des émois mystiques que cela m'inspire.
Dernière édition par Petitagore le Dim 29 Mar 2015 - 19:05, édité 1 fois (Raison : levée d'une ambiguïté)
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Lun 30 Mar 2015 - 17:43
Eh bien, l'interrogation métaphysique que tout cela me donne fichtrement envie de formuler, c'est: à quoi reconnaît-on l'intervention de l'intelligence?
Camarades athées, mes semblables mes frères, je vous sais méfiants et à fort juste titre dès qu'on vous sert l'argument de l'horloge et de l'horloger du petit père Voltaire:
"L'univers m'embarrasse, et je ne puis songer
Que cette horloge existe et n'ait point d'horloger."
Mais ne montez pas tout de suite sur vos grands chevaux: je ne suis pas (encore) en train de vous parler de l'existence d'un Dieu auquel vous ne croyez pas, mais très égocentriquement de mon intelligence à moi. J'espère que vous n'allez pas immédiatement me demander de vous prouver mon existence en faisant valoir que vu que vous n'en avez rien à cirer c'est sur moi que repose en l'espèce la charge de la preuve... Dispensons-nous de cet argument mesquin, car en l'espèce il relèverait quelque peu de la mauvaise foi crasse.
J'existe, j'ose espérer que vous ne le contesterez pas, je suis l'inventeur d'un jeujeu de triangles et de deux méthodes de résolution des problèmes qui constituent ce jeujeu:
- une méthode (relativement) intelligible pour un matheux pas complètement inculte, à base de construction de cavexes (reportez-vous aux épisodes précédents);
- une méthode informatique dite de force brutale, difficilement intelligible pour quelqu'un qui n'a pas un certain background informatique, mais qui n'a absolument rien du tout de miraculeux: elle est difficile à expliquer mais pas du tout irrationnelle.
La première méthode mène à des résultats valides et facilement vérifiables, souvent assez élégants (avec votre permission, je ne chercherai pas ici à être modeste car ce n'est pas l'objet du débat).
La seconde méthode mène elle aussi à des résultats valides et facilement vérifiables, mais souvent marqués par une logique à ce point tordue et louftingue qu'on n'y reconnaît pas en première analyse l'intervention d'une intelligence humaine. Cela n'a rien pour nous étonner: nous savons qu'il s'agit de solutions trouvées par un automatisme aveugle, absolument dépourvu de tout souci d'élégance.
Les premières solutions, élaborées par mon cerveau humain, peuvent être qualifiées d'élégantes (ce dont je me fous, ce n'est pas l'objet du débat) mais surtout d'intelligentes: elles témoignent de ma compréhension du problème.
Les solutions emberlificotées et louftingues, trouvées par l'automatisme informatique, méritent-elles d'être qualifiées de stupides, ou au contraire, méritent-elles elles aussi d'être qualifiées d'intelligentes en dépit de leur inélégance?
Réponse stéréotypée du rationaliste moyen qui pense que je suis en train de lui faire le coup du Grand Architecte de l'Univers:
-- Ton automatisme ne comprend rien à ce qu'il fait, donc ces solutions ne sont pas intelligentes, point barre.
Admettons. Mais l'automatisme qui trouve ces solutions pas intelligentes, n'est-il pas un automatisme intelligent?
Hin hin. Ça y est, vous pigez le problème?
Eh bien, frères athées, je ne sais pas si ma réponse d'agnostique vous déstabilisera, mais je vous l'assène comme une vérité que seule une insigne mauvaise foi pourrait vous permettre de contester: non seulement l'automatisme qui mène à ces solutions alambiquées est intelligent, mais il témoigne de beaucoup plus d'intelligence que les solutions élégantes directement sorties de mon cerveau.
Ma méthode de résolution des grilles par construction de cavexes, je peux vous l'enseigner en quelques heures, et pour la comprendre vous n'avez pas besoin de dominer plus de savoir mathématique que celui qui vous a permis de passer votre brevet d'études du premier cycle, à l'âge de douze ou treize ans.
En revanche, pour reconstituer vous-mêmes le détail de ma méthode "force brutale" de résolution, il vous faudrait dominer tout un savoir algorithmique et informatique qui demande des années d'apprentissage, et un abondant ensemble de compétences en programmation qu'on ne peut acquérir avant d'avoir sensiblement dépassé le niveau du baccalauréat.
Ça a beau être moins élégant, c'est en fait beaucoup plus complexe.
Et ça, mes chéris, c'est bel et bien une pierre dans votre jardin.
Je vous sais tout fiérots d'avoir démontré (car en effet, c'est bel et bien démontré) que la complexité du vivant n'est pas le résultat des gamberges d'un Dieu travaillant en Grand Architecte sur du papier calque et une planche à dessin. L'évolution est le résultat d'innombrables essais effectués au hasard par la sélection naturelle, c'est vrai, et l'examen du registre fossile en a apporté de telles quantités de preuves qu'à moins que d'être un taliban décérébré on n'en peut douter. Qui plus est, vous connaissez une petite poignée (assez petite, en fait) d'arguments qui démontrent que dans certains cas, l'évolution a accouché de solutions techniques complètement absurdes et dont la complexité pourrait très facilement être réduite par un être pensant, dans le genre de l'absurdité du trajet du nerf laryngé récurrent (l'argument préféré de Richard Dawkins: regardez ci-dessous à partir de 1:11):
Ces solutions tordues et absurdes dont l'évolution a accouché démontrent indubitablement que l'évolution emploie la force brutale des innombrables essais en lieu et place de la planche à dessin d'un Grand Architecte. Je vous l'accorde sans barguigner. Mais la maîtrise de la force brutale pour aboutir à un optimum au bout d'innombrables essais, êtes-vous conscients que c'est une méthode fort complexe et intelligente?
En tous les cas, c'est celle que j'emploie moi aussi pour aboutir automagiquement à des solutions qui marchent... Elles sont parfois, comme hier, ignominieusement tordues, mais aussi parfois d'une élégance qui me laisse pantois.
Certes, tout cela ne fait pas de moi un être miraculeux ni transcendant.
Mais je vous ferai quand même observer, frères athées, que moi qui suis à l'origine de ces solutions absurdes, tordues et fonctionnelles, je ne suis pas non plus un automatisme aveugle, inconscient et dépourvu de la moindre intelligence.
Et pan dans les dents.
(Note à mes contradicteurs furibards: merci de tenir compte dans vos répliques éventuelles du fait que je suis un agnostique et non un croyant)
Camarades athées, mes semblables mes frères, je vous sais méfiants et à fort juste titre dès qu'on vous sert l'argument de l'horloge et de l'horloger du petit père Voltaire:
"L'univers m'embarrasse, et je ne puis songer
Que cette horloge existe et n'ait point d'horloger."
Mais ne montez pas tout de suite sur vos grands chevaux: je ne suis pas (encore) en train de vous parler de l'existence d'un Dieu auquel vous ne croyez pas, mais très égocentriquement de mon intelligence à moi. J'espère que vous n'allez pas immédiatement me demander de vous prouver mon existence en faisant valoir que vu que vous n'en avez rien à cirer c'est sur moi que repose en l'espèce la charge de la preuve... Dispensons-nous de cet argument mesquin, car en l'espèce il relèverait quelque peu de la mauvaise foi crasse.
J'existe, j'ose espérer que vous ne le contesterez pas, je suis l'inventeur d'un jeujeu de triangles et de deux méthodes de résolution des problèmes qui constituent ce jeujeu:
- une méthode (relativement) intelligible pour un matheux pas complètement inculte, à base de construction de cavexes (reportez-vous aux épisodes précédents);
- une méthode informatique dite de force brutale, difficilement intelligible pour quelqu'un qui n'a pas un certain background informatique, mais qui n'a absolument rien du tout de miraculeux: elle est difficile à expliquer mais pas du tout irrationnelle.
La première méthode mène à des résultats valides et facilement vérifiables, souvent assez élégants (avec votre permission, je ne chercherai pas ici à être modeste car ce n'est pas l'objet du débat).
La seconde méthode mène elle aussi à des résultats valides et facilement vérifiables, mais souvent marqués par une logique à ce point tordue et louftingue qu'on n'y reconnaît pas en première analyse l'intervention d'une intelligence humaine. Cela n'a rien pour nous étonner: nous savons qu'il s'agit de solutions trouvées par un automatisme aveugle, absolument dépourvu de tout souci d'élégance.
Les premières solutions, élaborées par mon cerveau humain, peuvent être qualifiées d'élégantes (ce dont je me fous, ce n'est pas l'objet du débat) mais surtout d'intelligentes: elles témoignent de ma compréhension du problème.
Les solutions emberlificotées et louftingues, trouvées par l'automatisme informatique, méritent-elles d'être qualifiées de stupides, ou au contraire, méritent-elles elles aussi d'être qualifiées d'intelligentes en dépit de leur inélégance?
Réponse stéréotypée du rationaliste moyen qui pense que je suis en train de lui faire le coup du Grand Architecte de l'Univers:
-- Ton automatisme ne comprend rien à ce qu'il fait, donc ces solutions ne sont pas intelligentes, point barre.
Admettons. Mais l'automatisme qui trouve ces solutions pas intelligentes, n'est-il pas un automatisme intelligent?
Hin hin. Ça y est, vous pigez le problème?
Eh bien, frères athées, je ne sais pas si ma réponse d'agnostique vous déstabilisera, mais je vous l'assène comme une vérité que seule une insigne mauvaise foi pourrait vous permettre de contester: non seulement l'automatisme qui mène à ces solutions alambiquées est intelligent, mais il témoigne de beaucoup plus d'intelligence que les solutions élégantes directement sorties de mon cerveau.
Ma méthode de résolution des grilles par construction de cavexes, je peux vous l'enseigner en quelques heures, et pour la comprendre vous n'avez pas besoin de dominer plus de savoir mathématique que celui qui vous a permis de passer votre brevet d'études du premier cycle, à l'âge de douze ou treize ans.
En revanche, pour reconstituer vous-mêmes le détail de ma méthode "force brutale" de résolution, il vous faudrait dominer tout un savoir algorithmique et informatique qui demande des années d'apprentissage, et un abondant ensemble de compétences en programmation qu'on ne peut acquérir avant d'avoir sensiblement dépassé le niveau du baccalauréat.
Ça a beau être moins élégant, c'est en fait beaucoup plus complexe.
Et ça, mes chéris, c'est bel et bien une pierre dans votre jardin.
Je vous sais tout fiérots d'avoir démontré (car en effet, c'est bel et bien démontré) que la complexité du vivant n'est pas le résultat des gamberges d'un Dieu travaillant en Grand Architecte sur du papier calque et une planche à dessin. L'évolution est le résultat d'innombrables essais effectués au hasard par la sélection naturelle, c'est vrai, et l'examen du registre fossile en a apporté de telles quantités de preuves qu'à moins que d'être un taliban décérébré on n'en peut douter. Qui plus est, vous connaissez une petite poignée (assez petite, en fait) d'arguments qui démontrent que dans certains cas, l'évolution a accouché de solutions techniques complètement absurdes et dont la complexité pourrait très facilement être réduite par un être pensant, dans le genre de l'absurdité du trajet du nerf laryngé récurrent (l'argument préféré de Richard Dawkins: regardez ci-dessous à partir de 1:11):
Ces solutions tordues et absurdes dont l'évolution a accouché démontrent indubitablement que l'évolution emploie la force brutale des innombrables essais en lieu et place de la planche à dessin d'un Grand Architecte. Je vous l'accorde sans barguigner. Mais la maîtrise de la force brutale pour aboutir à un optimum au bout d'innombrables essais, êtes-vous conscients que c'est une méthode fort complexe et intelligente?
En tous les cas, c'est celle que j'emploie moi aussi pour aboutir automagiquement à des solutions qui marchent... Elles sont parfois, comme hier, ignominieusement tordues, mais aussi parfois d'une élégance qui me laisse pantois.
Certes, tout cela ne fait pas de moi un être miraculeux ni transcendant.
Mais je vous ferai quand même observer, frères athées, que moi qui suis à l'origine de ces solutions absurdes, tordues et fonctionnelles, je ne suis pas non plus un automatisme aveugle, inconscient et dépourvu de la moindre intelligence.
Et pan dans les dents.
(Note à mes contradicteurs furibards: merci de tenir compte dans vos répliques éventuelles du fait que je suis un agnostique et non un croyant)
Dernière édition par Petitagore le Sam 5 Sep 2015 - 19:27, édité 1 fois
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Invité Lun 30 Mar 2015 - 19:14
Ayé, come back, puisqu'il fallait absolument firefox pour jouer...
Le mien bugguait même en le réinstallant.
Du coup, je me suis sérieusement occupée de ce logiciel coquinou qui voulait faire la fête dans l'ordi en toute impunité, et qui me bloquait firefox. Zou.
Ce fut une longue bataille, il a voulu se cacher partout, bloquer toute possibilité de se faire "joyeusement" supprimer de l'ordi, même les antivirus et anti-malware ne le choppaient pas, ni la suppression, il bloquait tout.
hi hi. Viré à midi en lui coupant ailes et racines, sur une manœuvre subtile. Non mais. Et reviré le dernier bout ce soir.
Virus, malware,
"Souviens-toi que le Temps est un joueur avide
Qui gagne sans tricher, à tout coup ! c'est la loi." (citation)
Si Baudelaire avait pu croiser Voltaire, dans une immense et éternelle Horloge...
S'il est permis de tic-taquer au sujet de Voltaire qui fut cité, en ce vaste sujet arborescent et prolifique.
Le mien bugguait même en le réinstallant.
Du coup, je me suis sérieusement occupée de ce logiciel coquinou qui voulait faire la fête dans l'ordi en toute impunité, et qui me bloquait firefox. Zou.
Ce fut une longue bataille, il a voulu se cacher partout, bloquer toute possibilité de se faire "joyeusement" supprimer de l'ordi, même les antivirus et anti-malware ne le choppaient pas, ni la suppression, il bloquait tout.
hi hi. Viré à midi en lui coupant ailes et racines, sur une manœuvre subtile. Non mais. Et reviré le dernier bout ce soir.
Virus, malware,
"Souviens-toi que le Temps est un joueur avide
Qui gagne sans tricher, à tout coup ! c'est la loi." (citation)
Si Baudelaire avait pu croiser Voltaire, dans une immense et éternelle Horloge...
S'il est permis de tic-taquer au sujet de Voltaire qui fut cité, en ce vaste sujet arborescent et prolifique.
Invité- Invité
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Pieyre Mar 31 Mar 2015 - 14:22
On peut se poser la question d'une façon métaphysique. Mais on peut aussi examiner ce à quoi elle peut donner lieu quand on s'en dispense.Petitagore a écrit:Eh bien, l'interrogation métaphysique que tout cela me donne fichtrement envie de formuler, c'est: à quoi reconnaît-on l'intervention de l'intelligence?
Considérons l'être humain observable et le logiciel informatique comme des systèmes (en un sens restreint de la définition en systémique), en ne prenant en compte qu'une certaine classe de problèmes qu'ils auront à traiter. Ces systèmes ont des entrées, des sorties, et à l'intérieur ça mouline pour résoudre les problèmes.
Alors on peut s'intéresser à l'intelligence dans le sens de la simple capacité à les résoudre. Plus un système résout de problèmes, et plus rapidement il le fait, plus on le dira intelligent relativement à cette performance.
Petitagore existe; je l'ai rencontré. Mais est-ce que cela compte vraiment ? Tu es l'inventeur de deux méthodes, certes, l'une implémentée sous la forme d'un logiciel qui tourne (qui constitue un système donc) et l'autre sous la forme d'une explication écrite que tu es capable de mettre en œuvre (et tout lecteur on peut l'espérer). Mais ne serait-il pas possible de la programmer elle aussi ? Tu aurais alors deux logiciels dont on pourrait comparer l'intelligence en termes de performances, voire même d'élégance (encore faudrait-il trouver un critère permettant de l'évaluer).J'existe, j'ose espérer que vous ne le contesterez pas, je suis l'inventeur d'un jeujeu de triangles et de deux méthodes de résolution des problèmes qui constituent ce jeujeu:
- une méthode (relativement) intelligible pour un matheux pas complètement inculte, à base de construction de cavexes (reportez-vous aux épisodes précédents);
- une méthode informatique dite de force brutale, difficilement intelligible pour quelqu'un qui n'a pas un certain background informatique, mais qui n'a absolument rien du tout de miraculeux: elle est difficile à expliquer mais pas du tout irrationnelle.
Cela repose sur une conception de la compréhension comme disposition intrinsèque à la personne. N'est-ce pas une hypothèse métaphysique ? A contrario on peut estimer qu'un système comprend un problème dès lors qu'il peut se le représenter et disposer de méthodes pour le résoudre. Et pour moi il est possible qu'un logiciel en soit capable relativement à la classe des problèmes pour lesquels il est écrit. Ainsi en programmation fonctionnelle on définit le problème; c'est donc bien qu'il est représenté avant d'être résolu.Les premières solutions, élaborées par mon cerveau humain, peuvent être qualifiées d'élégantes (ce dont je me fous, ce n'est pas l'objet du débat) mais surtout d'intelligentes: elles témoignent de ma compréhension du problème.
Dernière édition par Pieyre le Mer 1 Avr 2015 - 0:11, édité 1 fois (Raison : un mot en trop)
Pieyre- Messages : 20908
Date d'inscription : 17/03/2012
Localisation : Quartier Latin
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Mer 1 Avr 2015 - 0:07
Depuis maintenant plus d'un mois que j'alimente ce fil de discussion, je pense avoir désormais assez préparé les esprits pour oser vous révéler enfin une incroyable vérité sur le Triancey partrois.
Ce jeu a des pouvoirs paranormaux.
Aussi incroyable que cela puisse vous paraître, la résolution d'une grille Triancey attire des bénédictions sur la tête de son auteur. Quiconque résoud une grille Triancey en se concentrant avec ferveur sur une aspiration la verra se réaliser -- peut-être pas systématiquement, mais vraiment dans d'innombrables cas --, à la seule condition qu'il manifeste assez de foi en la logique et de pureté d'âme pour s'en rendre digne.
Oh, je sens bien que vos esprits rationnels se récrient aussitôt... Je comprends cette incrédulité, longtemps elle a été la mienne; mais je sais aujourd'hui à quel point je me trompais. Je vous en conjure, lisez jusqu'au bout ce que j'écris ici, si vous y tenez vous vous esclafferez bruyamment quand j'aurai fini de vous expliquer, mais en attendant lisez-moi très attentivement. Je ne vous demande qu'un peu de votre temps, et si ce que j'ai à vous révéler est bel et bien la vérité comme je vous l'affirme, alors la lecture de ce texte représentera peut-être le tournant de votre vie, et vous mettra définitivement à l'abri de la tristesse, de l'angoisse et du désespoir, en un mot du malheur.
Oui, vous pouvez attirer les bénédictions sur votre tête. Ce pouvoir extraordinaire existe en chaque homme, et les plus lointains de nos ancêtres l'avaient déjà compris. Car l'humanité a toujours prié, vous le savez, et en dépit du rationalisme obtus dont notre siècle vous impose la dictature, vous savez aussi que dans d'innombrables cas ses prières ont été exaucées.
Pourquoi ce qui était possible hier serait-il aujourd'hui hors de portée? En réalité, nos prières n'ont perdu leur efficacité que parce que nous ne croyons plus aux divinités de nos ancêtres. Et sans doute avons-nous raison, d'un strict point de vue rationnel! Mais la bienveillance divine est toujours là, elle est toujours disposée à répondre à nos prières, à la seule condition que la foi soit au rendez-vous.
Vous n'avez plus la foi dans les dieux de vos ancêtres, et sans doute le justifieriez-vous sans peine: ces croyances, en effet, étaient parfois ridicules. Je vous comprends: je suis moi-même un rationaliste assez rigide, parfois même obtus; je m'en flatte, j'irai jusqu'à le revendiquer! Mais la foi reste puissante, à la seule condition que vous appreniez à la diriger vers ce en quoi vous croyez absolument.
Moi qui vous parle, je crois -- et de façon totalement rationnelle! -- à la puissance de la Logique. Et, aussi sidérant que cela vous paraisse -- que cela m'a paru! --, cette foi rationnelle a autant sinon plus de puissance que les croyances superstitieuses de nos ancêtres.
Entrez dans n'importe quelle vieille église de France, et voyez sur les murs ces innombrables ex-votos par lesquels nos ancêtres même pas lointains témoignaient de leur reconnaissance à la Sainte Vierge, à saint Antoine de Padoue, à sainte Rita: merci pour une guérison, merci pour une réussite à un examen, merci pour être revenu sain et sauf de la guerre... Je ne crois pas plus que vous à l'intervention personnelle des saints du paradis catholique, mais je constate un fait, que vous non plus ne pouvez nier: des hommes comme vous, pas plus sots que vous, ont prié avec ferveur, et ils ont été exaucés. Comment l'expliquer, sinon en constatant la puissance de la foi?
La seule chose qui vous empêche d'être exaucés vous aussi, c'est que vous ne savez pas où envoyer la foi dont vous êtes toujours capables. Vous n'êtes pas capable de croire à l'intervention de la Sainte Vierge? Alors ne priez pas la Sainte Vierge. Mais vous croyez à la Mathématique, à la Logique, au raisonnement rationnel? Alors, priez-les! Comprenez à quelle puissance donne accès la foi, votre foi. Croyez fermement en la Mathématique et la Logique, et vous serez exaucé. Quand la prière fervente est accompagnée d'une foi inébranlable, elle est exaucée, c'est aussi simple que cela. Il en a toujours été ainsi depuis que l'homme existe.
Et moi, je crois! Et vous comme moi, nous croyons!
Je ne crois guère à la bonté de sainte Rita, pas beaucoup plus à la bienveillance de la Sainte Vierge... en fait, je ne crois même à aucune de ces sornettes anachroniques. Mais je crois, et très profondément, à l'existence de la Mathématique, et à la puissance de la Logique.
Cela aussi, c'est de la foi!
Cela aussi, cela peut soulever des montagnes!
J'ai désormais résolu assez de grilles pour vous l'affirmer sans nuances: résoudre une grille Triancey, c'est attirer les bénédictions sur sa tête.
Cela commence modestement -- la vraie dévotion peut se placer dans de petites choses. C'était un matin de juin 2012, j'allais me mettre aux fourneaux pour cuisiner un gratin de chou-fleur, et j'ai voulu me distraire cinq minutes en résolvant une petite grille Triancey; je ne sais hélas plus laquelle, mais je me souviens que c'était un "cinq ou huit" difficile. Bien que la grille comportât deux quadrilatères, j'en vins à bout très rapidement, car j'avais bien raisonné, bien repéré le couple de pentagones à partir duquel il fallait construire le cavexe. La grille résolue, plein de joie et d'optimisme, je me mis à la confection de mon gratin, et... ce fut comme si l'esprit de la géométrie lui-même guidait ma main. Je coupai artistement les bouquets de chou-fleur, je parvins à les cuire juste à point, j'obtins sans effort la consistance parfaite pour ma Béchamel... C'était déjà à peine croyable, mais au moment d'assaisonner, le doute n'était plus permis: l'esprit de Triancey guidait ma main, et je dosai la muscade, la cannelle et le cumin (sans oublier une pointe d'ail) avec tant de précision que le plat fut un véritable régal, digne des plus grands cuisiniers -- or, jusque là, j'avais systématiquement raté tous mes plats! Sans exception! Comment peut-on expliquer cela autrement que par l'intervention des puissances célestes?
Un miracle, un vrai miracle.
Le lendemain, le fils d'une amie passait l'oral de français au baccalauréat. Je résolus de l'aider et attaquai une grille facile, de celles qu'on peut terminer sur un couloir de huit cases. Mais je réfléchis soigneusement, et je parvins à atteindre l'optimum sans avoir recours une seule fois aux touches de magnétophone permettant les retours en arrière. Eh bien, le soir même, mon amie m'appela: figurez-vous que son fils avait eu 17! Or il n'avait rien révisé, et avait été interrogé sur un texte de Montesquieu très difficile, rempli de locutions latines dont il ignorait le sens! Pour moi, le doute n'était plus permis.
Depuis, chaque fois que je dois prendre le train, je résous une grille de Triancey pour m'assurer que le voyage se passera bien. Et non seulement j'arrive toujours à la gare à l'heure (ce à quoi, à la rigueur, on pourrait chercher une explication rationnelle), mais en plus je suis systématiquement assis devant des gens souriants et charmants! Avouez que ça n'est pas commun. Comment l'expliquez-vous, si ce n'est par la puissance des grilles Triancey, et l'infinie bonté des esprits mathématiques?
En juillet 2013, j'eus cependant une déconvenue. J'avais résolu une grille difficile, je pensais donc pouvoir voyager sans problème, or c'était important car je devais prendre le train pour Limoges. Mais à Montparnasse, le bus 91 tardant trop à arriver, je me résolus à prendre le métro pour aller jusqu'à la gare d'Austerlitz -- et une incroyable malchance occasionna un arrêt de la rame de plus de cinq minutes, quelque part entre Sèvres-Babylone et Mabillon. Je n'invente rien: je me souviens extrêmement bien de m'être fait la réflexion que c'était vraiment une grande malchance, pour un cartésien comme moi, que d'être bloqué par Mabillon (car vous le savez, le grand Descartes et Mabillon partagent le même caveau en l'église Saint-Germain-des-Prés). Eh bien, quand finalement j'arrivai en courant, suant et essoufflé, sur le quai de la gare d'Austerlitz, le train venait de partir -- mais vraiment à l'instant, si je n'avais pas été chargé de bagages j'aurais sans doute réussi à monter en marche. Quelle malchance, me dis-je.
Fou que j'étais.
Car c'était le 12 juillet 2013, et mon train dérailla à Brétigny-sur-Orge, causant la mort de sept personnes.
Donc, vraiment, je vous l'assure, la résolution d'une grille Triancey attire sur la tête de celui qui la réussit... au bas mot autant de bénédictions qu'une neuvaine à sainte Rita!
Et ce que j'apprécie particulièrement dans cet acte de dévotion à la logique, c'est qu'il reste une action rationnelle de bout en bout -- comme les pages précédentes de ce fil vous en auront, je l'espère, convaincus. A la différence de tous les rituels superstitieux, il ne nie pas l'existence de l'impossible. Bien au contraire, il fonde sa démarche logique sur l'évitement d'icelui: c'est précisément en reconnaissant l'impossibilité d'aboutir à la prise intégrale de la grille que le sectateur du Triancey partrois peut parvenir à identifier, parmi les innombrables séquences de coups que pourrait engendrer le hasard, les quelques rarissimes qui permettent et ont permis de toute éternité d'approcher jusqu'à le toucher le score optimal d'une grille. Et c'est cette rationalité, je le suppose, qui réjouit assez l'esprit de la Logique pour faire presque à coup sûr intervenir sa puissance surnaturelle.
La résolution d'une grille Triancey est, je le crois, d'une puissance invocatoire particulière, car elle réjouit simultanément deux esprits mathématiques de magnitudes et de splendeurs très différentes: l'esprit bienveillant de la géométrie torique -- si rarement invoqué alors que son pouvoir n'est pas moins infini que celui de son grand frère, l'esprit de la géométrie euclidienne --, et d'autre part l'esprit infaillible du calcul arithmétique sur des entiers, père d'une multitude infinie de vérités démontrables. Résoudre une grille Triancey, c'est donc invoquer la Vérité éternelle dans ce qu'elle a de plus grand et de plus humble, de plus puissant et de plus simple. C'est donc couvrir d'une multitude de bénédictions son âme raisonnante, et confier notre fragilité humaine à l'indestructible et infinie bienveillance de la Mathématique.
La supplication fervente du juste a beaucoup de puissance, nous a enseigné l'apôtre Jacques. Que dirons-nous alors des orations ferventes à la Logique qui peuvent émaner de l'esprit rationnel d'un mathématicien rigoureux? Et si nos faibles capacités de raisonnement peuvent venir à bout d'une grille Triancey complète, les esprits omniscients de la rationalité et de la Logique ne pourront-ils pas faire bien mieux pour nous, mécréants que nous sommes?
Pour attirer sur vous la bonne fortune, ne perdez donc point de temps à vous procurer des cordes de pendu ou à toucher les pompons des marins; seuls des esprits stupides peuvent accorder du crédit à des superstitions aussi ridicules. Optez pour le Triancey partrois, première et seule superstition rationnelle de l'histoire.
Gloire et louanges à la Logique, qui gouverne le monde en ses moindres recoins pour les siècles des siècles! Ramen.
Ce jeu a des pouvoirs paranormaux.
Aussi incroyable que cela puisse vous paraître, la résolution d'une grille Triancey attire des bénédictions sur la tête de son auteur. Quiconque résoud une grille Triancey en se concentrant avec ferveur sur une aspiration la verra se réaliser -- peut-être pas systématiquement, mais vraiment dans d'innombrables cas --, à la seule condition qu'il manifeste assez de foi en la logique et de pureté d'âme pour s'en rendre digne.
Oh, je sens bien que vos esprits rationnels se récrient aussitôt... Je comprends cette incrédulité, longtemps elle a été la mienne; mais je sais aujourd'hui à quel point je me trompais. Je vous en conjure, lisez jusqu'au bout ce que j'écris ici, si vous y tenez vous vous esclafferez bruyamment quand j'aurai fini de vous expliquer, mais en attendant lisez-moi très attentivement. Je ne vous demande qu'un peu de votre temps, et si ce que j'ai à vous révéler est bel et bien la vérité comme je vous l'affirme, alors la lecture de ce texte représentera peut-être le tournant de votre vie, et vous mettra définitivement à l'abri de la tristesse, de l'angoisse et du désespoir, en un mot du malheur.
Oui, vous pouvez attirer les bénédictions sur votre tête. Ce pouvoir extraordinaire existe en chaque homme, et les plus lointains de nos ancêtres l'avaient déjà compris. Car l'humanité a toujours prié, vous le savez, et en dépit du rationalisme obtus dont notre siècle vous impose la dictature, vous savez aussi que dans d'innombrables cas ses prières ont été exaucées.
Pourquoi ce qui était possible hier serait-il aujourd'hui hors de portée? En réalité, nos prières n'ont perdu leur efficacité que parce que nous ne croyons plus aux divinités de nos ancêtres. Et sans doute avons-nous raison, d'un strict point de vue rationnel! Mais la bienveillance divine est toujours là, elle est toujours disposée à répondre à nos prières, à la seule condition que la foi soit au rendez-vous.
Vous n'avez plus la foi dans les dieux de vos ancêtres, et sans doute le justifieriez-vous sans peine: ces croyances, en effet, étaient parfois ridicules. Je vous comprends: je suis moi-même un rationaliste assez rigide, parfois même obtus; je m'en flatte, j'irai jusqu'à le revendiquer! Mais la foi reste puissante, à la seule condition que vous appreniez à la diriger vers ce en quoi vous croyez absolument.
Moi qui vous parle, je crois -- et de façon totalement rationnelle! -- à la puissance de la Logique. Et, aussi sidérant que cela vous paraisse -- que cela m'a paru! --, cette foi rationnelle a autant sinon plus de puissance que les croyances superstitieuses de nos ancêtres.
Entrez dans n'importe quelle vieille église de France, et voyez sur les murs ces innombrables ex-votos par lesquels nos ancêtres même pas lointains témoignaient de leur reconnaissance à la Sainte Vierge, à saint Antoine de Padoue, à sainte Rita: merci pour une guérison, merci pour une réussite à un examen, merci pour être revenu sain et sauf de la guerre... Je ne crois pas plus que vous à l'intervention personnelle des saints du paradis catholique, mais je constate un fait, que vous non plus ne pouvez nier: des hommes comme vous, pas plus sots que vous, ont prié avec ferveur, et ils ont été exaucés. Comment l'expliquer, sinon en constatant la puissance de la foi?
La seule chose qui vous empêche d'être exaucés vous aussi, c'est que vous ne savez pas où envoyer la foi dont vous êtes toujours capables. Vous n'êtes pas capable de croire à l'intervention de la Sainte Vierge? Alors ne priez pas la Sainte Vierge. Mais vous croyez à la Mathématique, à la Logique, au raisonnement rationnel? Alors, priez-les! Comprenez à quelle puissance donne accès la foi, votre foi. Croyez fermement en la Mathématique et la Logique, et vous serez exaucé. Quand la prière fervente est accompagnée d'une foi inébranlable, elle est exaucée, c'est aussi simple que cela. Il en a toujours été ainsi depuis que l'homme existe.
Et moi, je crois! Et vous comme moi, nous croyons!
Je ne crois guère à la bonté de sainte Rita, pas beaucoup plus à la bienveillance de la Sainte Vierge... en fait, je ne crois même à aucune de ces sornettes anachroniques. Mais je crois, et très profondément, à l'existence de la Mathématique, et à la puissance de la Logique.
Cela aussi, c'est de la foi!
Cela aussi, cela peut soulever des montagnes!
J'ai désormais résolu assez de grilles pour vous l'affirmer sans nuances: résoudre une grille Triancey, c'est attirer les bénédictions sur sa tête.
Cela commence modestement -- la vraie dévotion peut se placer dans de petites choses. C'était un matin de juin 2012, j'allais me mettre aux fourneaux pour cuisiner un gratin de chou-fleur, et j'ai voulu me distraire cinq minutes en résolvant une petite grille Triancey; je ne sais hélas plus laquelle, mais je me souviens que c'était un "cinq ou huit" difficile. Bien que la grille comportât deux quadrilatères, j'en vins à bout très rapidement, car j'avais bien raisonné, bien repéré le couple de pentagones à partir duquel il fallait construire le cavexe. La grille résolue, plein de joie et d'optimisme, je me mis à la confection de mon gratin, et... ce fut comme si l'esprit de la géométrie lui-même guidait ma main. Je coupai artistement les bouquets de chou-fleur, je parvins à les cuire juste à point, j'obtins sans effort la consistance parfaite pour ma Béchamel... C'était déjà à peine croyable, mais au moment d'assaisonner, le doute n'était plus permis: l'esprit de Triancey guidait ma main, et je dosai la muscade, la cannelle et le cumin (sans oublier une pointe d'ail) avec tant de précision que le plat fut un véritable régal, digne des plus grands cuisiniers -- or, jusque là, j'avais systématiquement raté tous mes plats! Sans exception! Comment peut-on expliquer cela autrement que par l'intervention des puissances célestes?
Un miracle, un vrai miracle.
Le lendemain, le fils d'une amie passait l'oral de français au baccalauréat. Je résolus de l'aider et attaquai une grille facile, de celles qu'on peut terminer sur un couloir de huit cases. Mais je réfléchis soigneusement, et je parvins à atteindre l'optimum sans avoir recours une seule fois aux touches de magnétophone permettant les retours en arrière. Eh bien, le soir même, mon amie m'appela: figurez-vous que son fils avait eu 17! Or il n'avait rien révisé, et avait été interrogé sur un texte de Montesquieu très difficile, rempli de locutions latines dont il ignorait le sens! Pour moi, le doute n'était plus permis.
Depuis, chaque fois que je dois prendre le train, je résous une grille de Triancey pour m'assurer que le voyage se passera bien. Et non seulement j'arrive toujours à la gare à l'heure (ce à quoi, à la rigueur, on pourrait chercher une explication rationnelle), mais en plus je suis systématiquement assis devant des gens souriants et charmants! Avouez que ça n'est pas commun. Comment l'expliquez-vous, si ce n'est par la puissance des grilles Triancey, et l'infinie bonté des esprits mathématiques?
En juillet 2013, j'eus cependant une déconvenue. J'avais résolu une grille difficile, je pensais donc pouvoir voyager sans problème, or c'était important car je devais prendre le train pour Limoges. Mais à Montparnasse, le bus 91 tardant trop à arriver, je me résolus à prendre le métro pour aller jusqu'à la gare d'Austerlitz -- et une incroyable malchance occasionna un arrêt de la rame de plus de cinq minutes, quelque part entre Sèvres-Babylone et Mabillon. Je n'invente rien: je me souviens extrêmement bien de m'être fait la réflexion que c'était vraiment une grande malchance, pour un cartésien comme moi, que d'être bloqué par Mabillon (car vous le savez, le grand Descartes et Mabillon partagent le même caveau en l'église Saint-Germain-des-Prés). Eh bien, quand finalement j'arrivai en courant, suant et essoufflé, sur le quai de la gare d'Austerlitz, le train venait de partir -- mais vraiment à l'instant, si je n'avais pas été chargé de bagages j'aurais sans doute réussi à monter en marche. Quelle malchance, me dis-je.
Fou que j'étais.
Car c'était le 12 juillet 2013, et mon train dérailla à Brétigny-sur-Orge, causant la mort de sept personnes.
Donc, vraiment, je vous l'assure, la résolution d'une grille Triancey attire sur la tête de celui qui la réussit... au bas mot autant de bénédictions qu'une neuvaine à sainte Rita!
Et ce que j'apprécie particulièrement dans cet acte de dévotion à la logique, c'est qu'il reste une action rationnelle de bout en bout -- comme les pages précédentes de ce fil vous en auront, je l'espère, convaincus. A la différence de tous les rituels superstitieux, il ne nie pas l'existence de l'impossible. Bien au contraire, il fonde sa démarche logique sur l'évitement d'icelui: c'est précisément en reconnaissant l'impossibilité d'aboutir à la prise intégrale de la grille que le sectateur du Triancey partrois peut parvenir à identifier, parmi les innombrables séquences de coups que pourrait engendrer le hasard, les quelques rarissimes qui permettent et ont permis de toute éternité d'approcher jusqu'à le toucher le score optimal d'une grille. Et c'est cette rationalité, je le suppose, qui réjouit assez l'esprit de la Logique pour faire presque à coup sûr intervenir sa puissance surnaturelle.
La résolution d'une grille Triancey est, je le crois, d'une puissance invocatoire particulière, car elle réjouit simultanément deux esprits mathématiques de magnitudes et de splendeurs très différentes: l'esprit bienveillant de la géométrie torique -- si rarement invoqué alors que son pouvoir n'est pas moins infini que celui de son grand frère, l'esprit de la géométrie euclidienne --, et d'autre part l'esprit infaillible du calcul arithmétique sur des entiers, père d'une multitude infinie de vérités démontrables. Résoudre une grille Triancey, c'est donc invoquer la Vérité éternelle dans ce qu'elle a de plus grand et de plus humble, de plus puissant et de plus simple. C'est donc couvrir d'une multitude de bénédictions son âme raisonnante, et confier notre fragilité humaine à l'indestructible et infinie bienveillance de la Mathématique.
La supplication fervente du juste a beaucoup de puissance, nous a enseigné l'apôtre Jacques. Que dirons-nous alors des orations ferventes à la Logique qui peuvent émaner de l'esprit rationnel d'un mathématicien rigoureux? Et si nos faibles capacités de raisonnement peuvent venir à bout d'une grille Triancey complète, les esprits omniscients de la rationalité et de la Logique ne pourront-ils pas faire bien mieux pour nous, mécréants que nous sommes?
Pour attirer sur vous la bonne fortune, ne perdez donc point de temps à vous procurer des cordes de pendu ou à toucher les pompons des marins; seuls des esprits stupides peuvent accorder du crédit à des superstitions aussi ridicules. Optez pour le Triancey partrois, première et seule superstition rationnelle de l'histoire.
Gloire et louanges à la Logique, qui gouverne le monde en ses moindres recoins pour les siècles des siècles! Ramen.
Dernière édition par Petitagore le Dim 27 Sep 2015 - 20:38, édité 2 fois (Raison : on ne passe pas le bac en janvier)
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Invité Mer 1 Avr 2015 - 16:07
Petitagore a écrit:stauk a écrit:Disons que le défi ça serait de remplir la grille en un minimum de clics ?
C'est une piste pour faire des trucs rigolos, et je t'engage à la creuser, mais je peux aussi ajouter quelques critères esthétiques:
A mon avis, on est en présence d'un bon casse-tête quand l'objectif est simple et clairement défini, tout en étant difficile à atteindre. "Un minimum de clics", ce n'est pas assez défini (c'est quoi, le minimum: quatre, ou douze? et comment je fais pour le savoir?). Deuxième critère: il est bon que cet objectif soit toujours accessible, quelle que soit la grille, parce que c'est vraiment râlant de s'escrimer trois quarts d'heure sur une grille pour qu'ensuite le concepteur du jeu vienne la gueule enfarinée vous dire "c'était une grille insoluble, ha ha, je vous ai bien eus": moi, ça me donnerait envie de l'étriper.
Minimum de clics pour les premiers essais, c'est ça ?
J'ai vu des variantes en cours de route, c'est quel objectif précis pour toi là maintenant tout de suite non-quantiquement parlant ? ^^
Que je me base dessus, sinon je risque de te donner des réponses à côté en ayant compris de travers
Méthode visuelle globale pour ma part, avec mixage des méthodes et mémorisation des possibles, un peu comme de sentir l'harmonie du truc et ses sous-harmonies.
Puisque tu demandais la méthode utilisée.
C'est faire l'éponge qui s'imbibe au début (de tout ça, des possibles, des méthodes visuelles et de leurs résultats visuels), après ça suit tout seul. L'oeil voit où aller, où tester, ou sinon par quel coin passer
Invité- Invité
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Jeu 2 Avr 2015 - 9:57
Sur la suggestion de Kara Magic Whale, je pense que je finirai par accoucher d'un résumé des épisodes précédents, mais en attendant le problème du jour sera la résolution de la grille "simplet", une grille de difficulté moyenne, avec un quadrilatère et un octogone, rien de particulièrement stupéfiant.
S'il plaît à Dieu (si je n'oublie pas, si je n'ai pas autre chose sur le feu dans ces plages horaires), vous aurez des suggestions de cavexes en début d'après-midi, et les solutions complètes un peu avant 19:00, comme d'hab'.
Mais de toute façon, vous êtes désormais assez grands pour résoudre cette grille tous seuls en moins de cinq minutes (et je compte large). Non?
S'il plaît à Dieu (si je n'oublie pas, si je n'ai pas autre chose sur le feu dans ces plages horaires), vous aurez des suggestions de cavexes en début d'après-midi, et les solutions complètes un peu avant 19:00, comme d'hab'.
Mais de toute façon, vous êtes désormais assez grands pour résoudre cette grille tous seuls en moins de cinq minutes (et je compte large). Non?
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Jeu 2 Avr 2015 - 16:55
Voici donc comme promis les cavexes que je vous suggère pour la résolution de la grille "simplet". Je commence par celui-ci, qui à mon avis n'est pas le meilleur mais que j'ai trouvé avec mon cerveau (je ne veux pas dire par là que je suis génial, mais simplement qu'il n'était pas nécessaire d'avoir des pouvoirs paranormaux pour l'identifier).
Voici trois cavexes concis identifiés par mon solveur, et je les trouve excellents:
Et en voici trois autres, moins élégants mais tout à fait utilisables aussi:
Voilà. Comme de coutume, je préfère me limiter aux jolis cavexes "rondouillards", mais sur cette grille le solveur élaborait aussi pas mal de "cavexes à mortaise", non inversibles, notamment en tirant parti de la présence du quadrilatère (l'une des cases du quadrilatère tient lieu de tenon, et les trois autres cases constituant la mortaise pourront être prises en un coup gagnant). Ces solutions sont parfaitement valides aussi et peuvent même être imaginées par un humain, mais j'attends pour vous en donner un exemple qu'il se présente une grille où aucun cavexe rondouillard ne pourra être dessiné, je pense que ce sera plus pédagogique de vous montrer cette technique quand elle est absolument nécessaire, plutôt que de vous forcer à vous extasier devant les idées de Shadok de mon solveur.
Solutions complètes... plus tard, peut-être en début de soirée.
Voici trois cavexes concis identifiés par mon solveur, et je les trouve excellents:
Et en voici trois autres, moins élégants mais tout à fait utilisables aussi:
Voilà. Comme de coutume, je préfère me limiter aux jolis cavexes "rondouillards", mais sur cette grille le solveur élaborait aussi pas mal de "cavexes à mortaise", non inversibles, notamment en tirant parti de la présence du quadrilatère (l'une des cases du quadrilatère tient lieu de tenon, et les trois autres cases constituant la mortaise pourront être prises en un coup gagnant). Ces solutions sont parfaitement valides aussi et peuvent même être imaginées par un humain, mais j'attends pour vous en donner un exemple qu'il se présente une grille où aucun cavexe rondouillard ne pourra être dessiné, je pense que ce sera plus pédagogique de vous montrer cette technique quand elle est absolument nécessaire, plutôt que de vous forcer à vous extasier devant les idées de Shadok de mon solveur.
Solutions complètes... plus tard, peut-être en début de soirée.
Dernière édition par Petitagore le Lun 5 Déc 2016 - 14:11, édité 1 fois (Raison : faute d'accord)
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Jeu 2 Avr 2015 - 20:11
- Et voici les solutions complètes:
- Avec le premier cavexe (solution non informatique): 11 22 17 25 39 34 36 43 41 (hors du cavexe), 4 2 8 7 21 19 (dedans).
Avec le cavexe 0: 20 9 16 14 6 26 35 43 22 36 10 (hors du cavexe), 24 3 31 39 (dedans).
Avec le cavexe 1: 26 41 40 32 28 18 4 29 6 20 21 (hors du cavexe), 22 10 9 1 (dedans).
Avec le cavexe 2: 5 20 12 0 26 11 16 35 43 34 (hors du cavexe), 17 1 23 32 29 (dedans).
Avec le cavexe 3: 22 27 21 13 17 0 43 7 33 6 (hors du cavexe), 24 11 40 31 36 (dedans).
Avec le cavexe 4: 28 31 30 43 34 26 13 17 25 12 (hors du cavexe), 14 40 11 8 3 (dedans).
Avec le cavexe 5 (notez qu'il est facile à photographier mentalement, ce qui est toujours précieux): 12 28 26 14 42 41 25 4 18 (hors du cavexe), 17 15 30 0 31 36 (dedans).
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Ven 3 Avr 2015 - 10:30
Aujourd'hui, nous étudierons la grille "timide".
Je vous l'ai classée en "difficulté moyenne", parce qu'en effet elle ne se résout pas en un clin d'oeil et demande un peu de tâtonnements. Mais regardez sa structure complètement horizontale (il y a nettement cinq rangées horizontales); ça vous donne d'emblée une piste (que dis-je, une piste... un boulevard!) sur une façon possible de construire un bon cavexe: entourez-moi ce tore horizontalement, et pour choisir à quel niveau, prenez tout simplement celui où il vous est possible de le faire en y incluant le polygone final qui va bien, marié à un pentagone. Si vous avez bien étudié vos leçons (mes chers petits), ce cavexe doit tomber sous le sens après un tout petit minimum de réflexion.
Plus exactement, il y a un cavexe évident, décomposable en plusieurs variantes (mais parfaitement utilisable tel quel).
Allez, lancez-vous, ne me forcez pas à vous l'expliquer, c'est trop simple.
Je vous l'ai classée en "difficulté moyenne", parce qu'en effet elle ne se résout pas en un clin d'oeil et demande un peu de tâtonnements. Mais regardez sa structure complètement horizontale (il y a nettement cinq rangées horizontales); ça vous donne d'emblée une piste (que dis-je, une piste... un boulevard!) sur une façon possible de construire un bon cavexe: entourez-moi ce tore horizontalement, et pour choisir à quel niveau, prenez tout simplement celui où il vous est possible de le faire en y incluant le polygone final qui va bien, marié à un pentagone. Si vous avez bien étudié vos leçons (mes chers petits), ce cavexe doit tomber sous le sens après un tout petit minimum de réflexion.
Plus exactement, il y a un cavexe évident, décomposable en plusieurs variantes (mais parfaitement utilisable tel quel).
Allez, lancez-vous, ne me forcez pas à vous l'expliquer, c'est trop simple.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Ven 3 Avr 2015 - 14:28
Bon, ben c'est vraiment pas bien malin pour ceux qui ont bien étudié les épisodes précédents.
La grille "timide" a 42 cases. Si, comme il est de coutume et d'ailleurs presque indispensable, nous sacrifions 2 cases (bleues) au départ, il en restera 40, qui est un multiple de 3 majoré de 1 -- donc il faut finir sur un polygone convexe dont le nombre de cases soit lui-même un multiple de 3 majoré de 1... un heptagone. Le théorème de l'avant-dernier coup nous affirmant que l'avant-dernier coup doit être joué sur un pentagone, nous cherchons donc un heptagone marié à un pentagone.
Or il n'y a qu'un pentagone sur cette grille (les cases 17, 18, 21, 22, 23). On ne peut donc atteindre le score optimal qu'en jouant le dernier coup sur un heptagone marié avec (possédant deux cases en commun avec) le dit pentagone: soit le gros heptagone en haut à droite (5, 6, 7, 11, 17, 18, 12), soit (et c'est préférable pour rester dans la même zone horizontale que le pentagone) l'heptagone réparti sur les bords gauche et droit: 9, 14, 13 à gauche, 12, 18, 23, 24 à droite.
Clic dans 15, re-clic dans 16 pour achever d'emplir ce joli bandeau horizontal, et voici notre cavexe-ruban qui entoure très joliment le tore et donc tombe sous le sens, éééélémentaire mon cher Watson:
Il reste à trouver un moyen de démarrer la partie en remplissant les trois rangées horizontales non incluses dans le cavexe, avec cette petite difficulté qu'il y a un quadrilatère réparti autour des quatre coins de la grille (on reconnaît les bons joueurs de Triancey à leur façon de se débarrasser des quadrilatères), et ça, c'est un tout petit peu moins élémentaire. Ce n'est quand même pas bien malin non plus.
Solutions complètes (y compris celles faisant appel à d'autres cavexes) en début de soirée.
La grille "timide" a 42 cases. Si, comme il est de coutume et d'ailleurs presque indispensable, nous sacrifions 2 cases (bleues) au départ, il en restera 40, qui est un multiple de 3 majoré de 1 -- donc il faut finir sur un polygone convexe dont le nombre de cases soit lui-même un multiple de 3 majoré de 1... un heptagone. Le théorème de l'avant-dernier coup nous affirmant que l'avant-dernier coup doit être joué sur un pentagone, nous cherchons donc un heptagone marié à un pentagone.
Or il n'y a qu'un pentagone sur cette grille (les cases 17, 18, 21, 22, 23). On ne peut donc atteindre le score optimal qu'en jouant le dernier coup sur un heptagone marié avec (possédant deux cases en commun avec) le dit pentagone: soit le gros heptagone en haut à droite (5, 6, 7, 11, 17, 18, 12), soit (et c'est préférable pour rester dans la même zone horizontale que le pentagone) l'heptagone réparti sur les bords gauche et droit: 9, 14, 13 à gauche, 12, 18, 23, 24 à droite.
Clic dans 15, re-clic dans 16 pour achever d'emplir ce joli bandeau horizontal, et voici notre cavexe-ruban qui entoure très joliment le tore et donc tombe sous le sens, éééélémentaire mon cher Watson:
Il reste à trouver un moyen de démarrer la partie en remplissant les trois rangées horizontales non incluses dans le cavexe, avec cette petite difficulté qu'il y a un quadrilatère réparti autour des quatre coins de la grille (on reconnaît les bons joueurs de Triancey à leur façon de se débarrasser des quadrilatères), et ça, c'est un tout petit peu moins élémentaire. Ce n'est quand même pas bien malin non plus.
Solutions complètes (y compris celles faisant appel à d'autres cavexes) en début de soirée.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Ven 3 Avr 2015 - 22:49
Bon, allons-y pour les soluces de la grille "timide".
Pour le même prix, je vous indique des cavexes moins évidents mais parfaitement utilisables:
Et pour le plaisir d'être exhaustif, je vous signale qu'on pouvait aussi utiliser des "cavexes à mortaise" (pas rondouillards et pas inversibles). En voici trois assez jolis:
Je rappelle que pour les "cavexes à mortaise", les illustrations représentent le résultat des premiers coups de la partie en ordre chronologique, et non pas, comme je le fais généralement, le patatoïde qui sera pris à la fin de la partie, avec le polygone final en bleu.
- Avec le cavexe en ruban du post précédent:
- 32 28 26 30 39 33 36 5 8 2 (hors du cavexe), 15 16 21 18 (dedans).
Pour le même prix, je vous indique des cavexes moins évidents mais parfaitement utilisables:
- Et les solutions correspondantes:
- Avec le cavexe 1: 32 39 41 29 34 27 37 3 1 14 (hors du cavexe), 24 16 23 18 (dedans).
Avec le cavexe 2: 32 39 30 28 26 13 33 37 3 8 (hors du cavexe), 14 16 21 12 (dedans).
Avec le cavexe 2 étendu (un peu massif dans l'absolu, mais très utilisable ici): 19 41 0 25 24 30 28 (hors du cavexe), 9 35 38 4 15 21 5 (dedans).
Et pour le plaisir d'être exhaustif, je vous signale qu'on pouvait aussi utiliser des "cavexes à mortaise" (pas rondouillards et pas inversibles). En voici trois assez jolis:
Je rappelle que pour les "cavexes à mortaise", les illustrations représentent le résultat des premiers coups de la partie en ordre chronologique, et non pas, comme je le fais généralement, le patatoïde qui sera pris à la fin de la partie, avec le polygone final en bleu.
- Solutions avec les cavexes à mortaise:
- Avec le cavexe à mortaise 0: 11 0 41 6 38 36 25 3 19 (hors du cavexe), 16 28 30 22 14 (dedans).
Avec le cavexe à mortaise 1: 37 41 39 0 35 26 24 29 14 (hors du cavexe), 1 3 15 22 18 (dedans).
Avec le cavexe à mortaise 2: 7 29 39 4 41 1 10 36 20 (hors du cavexe), 11 19 32 17 9 (dedans).
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Sam 4 Avr 2015 - 11:56
Bon, je continue de prendre dans l'ordre les grilles de difficulté moyenne de mon inventaire, et comme j'entame la rubrique "présidents de la Ve République" du dit inventaire, la grille d'aujourd'hui portera le nom prestigieux de grille "degaulle".
Ah oui, mais c'est vrai que quand j'écris petit personne ne me lit. Donc je vous la refais. Ahem, le problème du jour sera la grille "degaulle".
De Gaulle était un grand homme (au moins par la taille, mais honnêtement je ne pense pas que ce soit la seule raison), mais la grille "degaulle" est une petite grille classique, pas du tout hors de votre portée.
J'ai vécu du temps de De Gaulle (soit dit en passant, on écrit généralement "de Gaulle", avec une minuscule, comme si Mongénéral avait eu une particule nobiliaire, mais ce n'est pas vrai: il avait un nom du Nord avec une majuscule, comme De Broukère). J'étais alors un petit garçon, et à l'époque le président de la Blikpuré, c'était l'héritier direct de Saint Louis, de Louis XIV et de Napoléon, vraiment vous n'imaginez pas. Obama, en comparaison, c'est vraiment un prolo. Non, à l'époque, De Gaulle, c'était pas tout à fait Dieu sur Terre, mais vraiment pas loin. Chaque fois que son nom était prononcé, on rectifiait la position, et on se mettait debout au garde-à-vous kif-kif que quand on entendait jouer la Marseillaise. Ah, ça vous avait une autre gueule que nos présidents à la "casse-toi pôv' con".
Ça n'empêchait pas De Gaulle d'être aussi, de l'avis de mon papa qui était le meilleur papa du monde, "un vieux con réactionnaire". Une brute fasciste. Un suppôt du colonialisme. Un fusilleur. Le fossoyeur des libertés publiques. Enfin ce genre de choses, quoi. A l'époque on croyait encore à l'importance du politique.
A l'époque, "la politique de la France ne se décidait pas à la Corbeille".
C'est loin, tout ça, mais ça avait quand même une autre gueule...
Bon, alors, vous me le trouvez, ce cavexe?
Ah oui, mais c'est vrai que quand j'écris petit personne ne me lit. Donc je vous la refais. Ahem, le problème du jour sera la grille "degaulle".
De Gaulle était un grand homme (au moins par la taille, mais honnêtement je ne pense pas que ce soit la seule raison), mais la grille "degaulle" est une petite grille classique, pas du tout hors de votre portée.
J'ai vécu du temps de De Gaulle (soit dit en passant, on écrit généralement "de Gaulle", avec une minuscule, comme si Mongénéral avait eu une particule nobiliaire, mais ce n'est pas vrai: il avait un nom du Nord avec une majuscule, comme De Broukère). J'étais alors un petit garçon, et à l'époque le président de la Blikpuré, c'était l'héritier direct de Saint Louis, de Louis XIV et de Napoléon, vraiment vous n'imaginez pas. Obama, en comparaison, c'est vraiment un prolo. Non, à l'époque, De Gaulle, c'était pas tout à fait Dieu sur Terre, mais vraiment pas loin. Chaque fois que son nom était prononcé, on rectifiait la position, et on se mettait debout au garde-à-vous kif-kif que quand on entendait jouer la Marseillaise. Ah, ça vous avait une autre gueule que nos présidents à la "casse-toi pôv' con".
Ça n'empêchait pas De Gaulle d'être aussi, de l'avis de mon papa qui était le meilleur papa du monde, "un vieux con réactionnaire". Une brute fasciste. Un suppôt du colonialisme. Un fusilleur. Le fossoyeur des libertés publiques. Enfin ce genre de choses, quoi. A l'époque on croyait encore à l'importance du politique.
A l'époque, "la politique de la France ne se décidait pas à la Corbeille".
C'est loin, tout ça, mais ça avait quand même une autre gueule...
Bon, alors, vous me le trouvez, ce cavexe?
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Invité Sam 4 Avr 2015 - 14:41
Je vais me pencher à comprendre exactement point par point les solutions que tu donnes Petitagore, j'ai l'impression de partir pour l'instant dans une direction différente de l'objectif en ayant mal compris ou en prenant des interprétations différentes.
Je préfère chercher au début par mes propres repères et tests, sans lire les solutions, mais là je crois que je vais aller voir pour intégrer l'objectif sans me tromper.
Découvrir trois cases à la fois, pile poil, sans compter celle où l'on clique ?
J'ai essayé hier en comptant celle du clic + max 2 autres découvertes, mais à voir la solution ci-dessus, cela semble clic + 3 cases (donc 4 au final en comptant le clic dedans, est-ce ça?).
Sorry d'aller lentement, mon ordi a encore des problèmes, et sur celui-ci je ne peux pas aller voir le logiciel, je dois attendre que mon conjoint libère le sien (qui est son outil de travail donc bien occupé, et quand il ne bosse pas, je quitte vite l'ordi pour passer du temps avec lui).
Pour celle de Timide, si je te copie le début de recherche afin d'aller dans le style que tu proposais, j'avais du coup commencé: 9. 19. 10. 20. 17. 18. 24 pour faire ensuite comme une pelure d'orange en spirale torrée. Cela me bloquait avec un bleu en chemin, que j'ai laissé sur les numéros, mais si c'est trois cases + le clic je comprends mieux pourquoi.
Intelligence naturaliste (pelure d'orange) pour résoudre cela en fonction de ce départ droit que tu indiquais (comme tu demandais comment on procédait): en mode torré c'est spatialement différent, mais l'idée est là.
Le cavexe pouvant être "l'arrondi" de début ou de fin. ^^
Je préfère chercher au début par mes propres repères et tests, sans lire les solutions, mais là je crois que je vais aller voir pour intégrer l'objectif sans me tromper.
Découvrir trois cases à la fois, pile poil, sans compter celle où l'on clique ?
J'ai essayé hier en comptant celle du clic + max 2 autres découvertes, mais à voir la solution ci-dessus, cela semble clic + 3 cases (donc 4 au final en comptant le clic dedans, est-ce ça?).
Sorry d'aller lentement, mon ordi a encore des problèmes, et sur celui-ci je ne peux pas aller voir le logiciel, je dois attendre que mon conjoint libère le sien (qui est son outil de travail donc bien occupé, et quand il ne bosse pas, je quitte vite l'ordi pour passer du temps avec lui).
Pour celle de Timide, si je te copie le début de recherche afin d'aller dans le style que tu proposais, j'avais du coup commencé: 9. 19. 10. 20. 17. 18. 24 pour faire ensuite comme une pelure d'orange en spirale torrée. Cela me bloquait avec un bleu en chemin, que j'ai laissé sur les numéros, mais si c'est trois cases + le clic je comprends mieux pourquoi.
Intelligence naturaliste (pelure d'orange) pour résoudre cela en fonction de ce départ droit que tu indiquais (comme tu demandais comment on procédait): en mode torré c'est spatialement différent, mais l'idée est là.
Le cavexe pouvant être "l'arrondi" de début ou de fin. ^^
Invité- Invité
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Sam 4 Avr 2015 - 17:06
Kara Magic whale a écrit:Découvrir trois cases à la fois, pile poil, sans compter celle où l'on clique ?
Ah, décidément il va falloir que je fasse quelque chose pour ceux qui prennent le film en marche...
Bon, alors, je l'écris en gras, et j'explique après: il faut prendre trois cases à la fois, pile poil, en comptant celle où l'on clique.
Plus exactement: le but du jeu est de prendre aussi souvent que possible trois cases à la fois, pas une de plus, pas une de moins. Si on y arrive, ça colore en jaune, sinon en bleu. Donc, quand on réussit, la grille est presque entièrement jaune. Mais il est impossible qu'elle soit entièrement jaune (oui, c'est frustrant, mais c'est la Logique en personne qui en a décidé ainsi). Il est en revanche possible (et c'est ça le vrai but du jeu) de réussir une série ininterrompue de coups gagnants (jaunes) entre les deux premiers (deux cases bleues isolées) et le tout dernier (un pentagone, un hexagone ou un heptagone bleu).
Je sais, c'est pas intuitif. C'est pour ça que je ne l'ai pas énoncé d'emblée en entamant ce fil, j'avais besoin de préparer les esprits.
De façon similaire, avant de nous balancer le Seigneur Jésus (qui prêche l'amour du prochain, au cas où vous ne seriez pas au courant), le Bon Dieu a pareillement envoyé des prophètes qui ont pareillement dit des tas de choses vraiment pas claires du tout, et qui occasionnellement donnent même furieusement l'impression de dire le contraire exact de l'enseignement du Messie dont ils étaient censés préparer la venue (du genre: faut exterminer les païens, mais alors vraiment bien, hein, jusqu'au tout dernier, femmes, enfants et bétail compris, et si en plus c'est dans d'horribles souffrances c'est encore mieux); bref, le Bon Dieu, s'il existe, a une pédagogie aussi désastreuse que la mienne, mais peut-être aussi qu'il cherche à nous faire comprendre des choses sensiblement plus compliquées que mon petit jeujeu -- raison pour laquelle l'humanité continue (hélas) de ne rien biter à l'amour du prochain, de même que les lecteurs de ce fil continuent de ne rien biter à mon petit jeujeu (ce qui est quand même moins grave mais me désole quand même, et à part ça j'ai le sentiment de commencer à être un peu hors sujet).
Le cavexe, ce concept fumeux dont je suis l'inventeur et dont je vous rebats les oreilles, regroupe un ensemble de cases sur lequel on jouera les derniers coups de la partie, pas son début. "Dessiner un cavexe", c'est fantasmer une fin de partie optimale. L'idée est de fantasmer la fin de la partie pour ensuite réussir le début. Oui, ça fait un peu Valérian agent spatio-temporel
, mais je crois quand même que c'est la bonne méthode: en toutes choses il faut considérer la fin...J'ai essayé hier en comptant celle du clic + max 2 autres découvertes, mais à voir la solution ci-dessus, cela semble clic + 3 cases (donc 4 au final en comptant le clic dedans, est-ce ça?).
Ben... non.
Sorry d'aller lentement, mon ordi a encore des problèmes, et sur celui-ci je ne peux pas aller voir le logiciel, je dois attendre que mon conjoint libère le sien (qui est son outil de travail donc bien occupé, et quand il ne bosse pas, je quitte vite l'ordi pour passer du temps avec lui).
Très bonne excuse.
En revanche, pour ce qui est de l'ergonomie, y a mieux...Pour celle de Timide, si je te copie le début de recherche afin d'aller dans le style que tu proposais, j'avais du coup commencé: 9. 19. 10. 20. 17. 18. 24 pour faire ensuite comme une pelure d'orange en spirale torrée. Cela me bloquait avec un bleu en chemin, que j'ai laissé sur les numéros, mais si c'est trois cases + le clic je comprends mieux pourquoi.
Je n'ai pas très bien compris ce que tu cherchais à faire, mais visiblement ce n'était pas ce que je préconisais: le cavexe décrit la zone où on jouera la fin de la partie, pas le début (l'idée est précisément de rendre cette zone taboue jusqu'à la fin de la partie!).
Intelligence naturaliste (pelure d'orange) pour résoudre cela en fonction de ce départ droit que tu indiquais (comme tu demandais comment on procédait): en mode torré c'est spatialement différent, mais l'idée est là.
C'est assurément une idée, mais j'ai furieusement l'impression que ce n'est pas celle que je cherche à faire passer!
Va vraiment falloir que je publie un résumé des épisodes précédents, mais j'ai introduit la vraie règle seulement à partir de ce post-ci, avec des compléments dans ce post-là: tout ce que j'ai dit auparavant servait à titiller la curiosité de mes lecteurs, mais ce n'était pas la vraie règle. Alors, évidemment, si tu as essayé de relire tout le fil en partant du début mais en t'arrêtant en amont du post fatidique et de son complément nécessaire, tu n'as pu que comprendre de travers. Toutes mes confuses, ma pédagogie était adaptée à ceux qui me suivaient depuis le début, pas à ceux qui sont arrivés ensuite.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Sam 4 Avr 2015 - 19:04
Ah, et puis on peut aussi signaler, toujours à l'intention des débutants, ce post qui donne un exemple détaillé de résolution d'une grille.
Dernière édition par Petitagore le Sam 4 Avr 2015 - 19:58, édité 1 fois (Raison : style exécrable)
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Petitagore Sam 4 Avr 2015 - 23:44
Eh bien, je crois que la grille "degaulle" peut être qualifiée d'inratable: c'est vraiment "à tous les coups l'on gagne": il suffit d'essayer un cavexe pour le réussir -- à la seule condition qu'on ait compris que le polygone final doit être un hexagone.
Allez, voici une petite tripotée de cavexes utilisables:
Solutions complètes... à la fin du week-end de Pâques.
Allez, voici une petite tripotée de cavexes utilisables:
Solutions complètes... à la fin du week-end de Pâques.
Petitagore- Messages : 6311
Date d'inscription : 29/11/2011
Age : 64
Localisation : Ile-de-France -
Re: Petit jeujeu mathématique deviendra gros casse-tête
par Invité Lun 6 Avr 2015 - 12:54
Merci pour les précisions, Petitagore. ^^
ça va aider et débroussailler.
Oui, cavexe pour la fin, j'avais vu ce point, c'est juste normal là pour ma façon de fonctionner.
ça va aider et débroussailler.
Oui, cavexe pour la fin, j'avais vu ce point, c'est juste normal là pour ma façon de fonctionner.
- Spoiler:
- j'ai besoin de tenter avant ce qui ne marche pas pour m'imprégner mieux de ce qui marche, une sorte de filet appréhendant à la fois le bon chemin et aussi les autres chemins inutiles, à la fois les pleins et les vides en même temps, c'est plus long que de juste trouver la bonne solution, mais ensuite cela m'optimise la vision globale.
Une habitude aussi de vouloir "retourner" pour voir ce que ça donne en faisant "à l'envers", "à l'inverse" ce que ça en dit, si c'est symétrique, chaotique, ou si cela émerge un autre code-langage visuel qui est intéressant à utiliser.
(je fais pareil avec certains livres, je les décortique à l'envers, en mettant le début à la fin, puis chemin chaotique de lecture en mélangeant les chapitres lus en désordre pendant la phase d'imprégnation, c'est un peu comme démonter la voiture avant de jouer-lire avec, envie de trouver la structure-squelette, en refaire le puzzle, en non-linéaire contrairement à la lecture qui suit l'ordre)
Invité- Invité
Page 3 sur 6 • 1, 2, 3, 4, 5, 6
Sujets similaires» Petit casse-tête à l'attention de ceux qui lancent des sorties ici :)
» Petit Zebron? Deviendra grand ?
» L'Amour.. Mon casse-tête zébré...
» L'art de m'en faire voir de 6 couleurs... Rubik's Cube [Casse-tête]
» Ca yest... mon petit a mal à la tête et au ventre à l'école
» Petit Zebron? Deviendra grand ?
» L'Amour.. Mon casse-tête zébré...
» L'art de m'en faire voir de 6 couleurs... Rubik's Cube [Casse-tête]
» Ca yest... mon petit a mal à la tête et au ventre à l'école
Page 3 sur 6
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum