Petit jeujeu mathématique deviendra gros casse-tête

Merci pour les précisions, Petitagore. ^^
ça va aider et débroussailler.

Oui, cavexe pour la fin, j'avais vu ce point, c'est juste normal là pour ma façon de fonctionner.

Spoiler:

Et voici comme promis plein plein de solutions pour la grille "degaulle".

Solutions complètes:

Personnellement, je vois aussi une action miraculeuse dans la beauté des grilles du Triancey bien que j'ai la paresse de me laisser aller à lire les explications sans expérimenter moi-même un algorithme de mon cru (la foi n'a rien à voir là-dedans, rassurez-vous).

J'ai toujours été fasciné par la topologie et je dois au Triancey une révélation sur les tores et leurs propriétés fabuleuses.

Mais pour réagir sur le 1er Avril et les miracles, je voudrais juste exposer une expérience super-naturelle que j'ai vécue ce matin:
Je me suis réveillé ce matin suite à un rêve et j'ai eu immédiatement l'idée d'aller en parler sur un forum où j'avais laissé un message la veille.
Il faut dire que le rêve était lié au message. Vous trouverez une copie de ce message sur le forum lié à la religion: "Noël, fête de l'Anté-Christ".

Ce message, loin de s'attaquer à la foi chrétienne, en était la défense, face à des manoeuvre de marketing de bas étage associées à l'église catholique.

Dans mon rêve, j'étais dénoncé puis interné à l'hôpital psychiatrique pour avoir osé exprimer une opinion qui avait choqué un lecteur.

En me réveillant, j'ai immédiatement pensé à mon message de la veille et j'ai voulu y ajouter un commentaire sur ce rêve.

Quelle n'a pas été ma stupéfaction de voir que pendant la nuit, une personne avait posté une réaction à mon message: la dernière phrase du message contenait 7 fois le mot rêve.

Comme le disait Monsieur Cyclopède: "Etonnant, n'est-ce pas?"

Pour revenir au poisson d'Avril: le poisson est le symbole des premiers chrétiens, remplacé par les romains par la croix. Faut-il voir dans la tradition du poisson d'avril, une manière romaine de se moquer des chrétiens qui sont restés attachés à la foi des premiers temps, par ceux qui ont choisi de suivre Rome et son culte papal?

Pour éviter toute ambiguité, je trouve l'article de petitagore très humoristique et dénué de toute volonté de se moquer de ceux qui ont la foi:
Je pense que l'on vit dans le monde auquel on croit.
Si on decouvre que ce n'est pas la vérité, c'est parce que l'on y croit plus.

Mais il faut bien choisir en quoi on croit car ce n'est pas sans conséquence:
si vous croyez que le monde est absurde, vous aurez un comportement absurde.
Si vous croyer que le monde est plein d'humour, vous aurez de la joie.
Si vous croyez que le monde est rempli d'amour pour vous, vous aurez de l'amour pour autrui.
Si vous aimez vraiement quelqu'un, vous êtes prêts à mourir pour lui.
Si vous choisissez d'être prêt à mourir pour Jésus, vous êtes chrétien.

Personnellement, je dois avouer que je ne donnerai pas ma vie pour le Triancey.
On voit ainsi que certaines croyances sont plus fortes que d'autres.
Si vous avez la foi dans les dieux de vos ancêtres, à quelle mesure jaugez-vous cette foi?

Bon, ben c'est bien beau tout ça, mais moi il faut que j'arrive au bout de mon inventaire, donc aujourd'hui nous allons résoudre une grille de plus. Le problème du jour sera la grille  "pompidou".



La plupart d'entre vous n'ont pas connu Georges Pompidou, bande de blancs-becs. C'était un type assez intelligent mais il n'en avait pas l'air, il faisait un peu l'effet d'un croisement entre Louis-Philippe et Raffarin. Un bon gros bourgeois français bien de chez nous, assez ordinaire pour ne pas paraître "de la haute", assez bien élevé et assez riche pour être toléré par la bonne société qui, je crois, l'a toujours considéré comme un roturier. Faut dire qu'avec un nom pareil, ça n'aide pas. A l'époque où tout le monde était résistant ou collabo, il était prof de français et s'intéressait à la poésie, assez pour être l'auteur d'une anthologie qui, paraît-il, témoigne d'un certain goût. A l'époque où tout le monde faisait carrière dans la politique, il a fait carrière dans la banque; pas comme guichetier, chez Rothschild (oui, ze Rothschild, l'objet de tous les fantasmes complotistes depuis que l'antisémitisme existe ou peu s'en faut). C'était un membre assez terne de la clique gaulliste, les fameux "copains et coquins" qui gravitaient autour du grand Charles Mongénéral. Il a fini par être bombardé Premier ministre, parce qu'il "faisait le job" et ne faisait d'ombre à personne. En mai 68, quand De Gaulle a plus ou moins perdu les pédales ou tout au moins eu un grand moment de découragement, c'est Pom-pom-pidou (comme on l'appelait en référence à une chanson de Marilyn Monroe) qui a négocié avec les syndicats, évitant l'émeute, mettant fin à la grève... Résultat, quand peu de mois après De Gaulle s'est barré en se drapant dans son mépris, Pompidou a été élu président de la République, et il a été un président "normal", comme dirait Hollande (mais l'économie allait nettement mieux). Il n'en a pas profité beaucoup, et il est mort "des suites d'une longue maladie", comme on disait à l'époque. On lui doit des tas de choses discutables: une loi de 73 qui a mis le pays sous la coupe des banques (sauf qu'il y était déjà, mais ça se voyait moins); des autoroutes (gratuites, de son temps); éééénormément de centrales nucléaires (la prochaine fois qu'un Fukushima pétera chez nous, ayez une pensée émue pour Pompidou); et le centre Beaubourg, qui témoigne de beaucoup d'audace architecturale en même temps que, faut bien le dire, d'un goût de chiottes. Pompidou s'intéressait à l'art moderne et ce n'était certainement pas l'aspect le plus détestable de sa personnalité, mais je pense qu'il avait plus de bonnes antennes pour capter ce qui se vendait bien qu'un vrai sens artistique. Paix à ses cendres. Sans être un type très estimable, je pense qu'il était sensiblement moins méprisable que notre clique politique actuelle, et j'aurais accepté de prendre le thé avec lui (mais je me serais quand même bien fait chier).

Toujours est-il que la grille "pompidou" est très, très, très pédagogique. La solution ne saute pas du tout aux yeux, mais alors vraiment pas du tout, en revanche un raisonnement rigoureux vous y mènera en droite ligne. Finalement, elle est assez dans l'esprit de son personnage éponyme: il n'y a pas de génie à y déployer, mais on peut y "faire le job" de façon méthodique, routinière et rentable (peu d'efforts pour un résultat payant). Cette grille vient tout droit des Trente Glorieuses, c'est clair.

C'est quand même dingue, les associations d'idées. Quand on me dit "pom-pom-pidou", j'arrive à penser simultanément à lui:



et à elle:



Et, encore plus fort, le premier n'arrive pas le moins du monde à me dégoûter de la seconde!

Pompidou / Pompe les sous, comme on disait aussi à l'époque.

Bon. Procédons méthodiquement pour la résolution de cette grille "pompidou" qui est pédagogique en diable.

Quelle est la première question à se poser? Ben, la même qu'à chaque fois: où doit-on jouer le dernier coup de la partie pour atteindre le score optimal? On le détermine de façon très simple, en fonction du nombre de cases. Cette grille a quarante cases, donc il faut terminer sur un couple de pentagones. Si ça ne vous paraît pas flagrant, c'est que vous avez mal potassé les chapitres précédents, mais ce n'est pas un péché mortel. Donc, je vous èquesplique, once again, pardon pour la répétition.

Le dernier coup d'une partie n'est jamais un coup gagnant, il prend toujours plus de trois cases. On n'y peut rien, en revanche, si on anticipe bien, on peut faire en sorte que ce dernier coup prenne aussi peu de cases que possible. Cela revient à jouer le dernier coup dans un polygone convexe aussi petit que possible... mais compte tenu de la contrainte que ce dernier coup devra, lui, être précédé d'une série de coups gagnants aussi longue que possible. Les coups gagnants prennent les cases trois par trois, les deux premiers coups de la partie ne peuvent pas prendre trois cases et il est donc préférable qu'ils ne prennent chacun qu'une case isolée (ça, je vous l'ai déjà expliqué sous les noms de théorème du premier coup et de théorème du deuxième coup)...

Mettons tout ça ensemble, et ça nous donne: quarante cases au total, moins deux cases sacrifiées au départ (reste 38), de quoi on soustrait encore un petit polygone convexe de façon que le reste soit un multiple de trois (pour permettre la série ininterrompue de coups gagnants, c'est-à-dire prenant trois cases à la fois, pas une de plus pas une de moins). Si on enlève un pentagone, ça nous fera 38 - 5 = 33 = 11 x 3 = 11 coups gagnants, et c'est ça l'optimum.

Donc le dernier coup (perdant, colorant les cases en bleu) devra être joué sur un pentagone. Et quid de l'avant-dernier coup? Il devra, lui, être un coup gagnant, donc prendre trois cases (colorées en jaune) à proximité immédiate du pentagone final. Donc cet avant-dernier coup devra être joué dans un polygone marié (ayant deux cases en commun) avec le pentagone final... autrement dit un autre pentagone.

Donc nous cherchons un couple de pentagones, deux pentagones mariés (ayant deux cases en commun).

Où y a-t-il cela sur la grille? Tip: ça ne se voit vraiment pas beaucoup, mais n'oubliez pas que la grille n'est pas un simple carré, c'est un tore; le bord gauche touche le bord droit, le bord supérieur touche le bord inférieur, toutes les cases qui touchent un coin sont en fait dans le même polygone.

Là, je n'en suis plus à vous donner un indice, mais carrément à vous indiquer la solution... Donc je le fais carrément: le couple de pentagones mariés, il est là:



D'accord, ça saute pas aux yeux. 0, 7, 8, 34, 39, ça fait cinq cases autour d'une même sommet (représenté quatre fois aux quatre coins du carré, mais il s'agit bien d'un seul et unique sommet sur le tore). 0, 1, 9, 8, 14, c'est aussi un pentagone, coupé en deux moitiés inégales sur les côtés gauche et droit, et marié par deux cases (8 et 0) avec le pentagone précédent. Donc, nous avons notre couple de pentagones. Certes, ça sautait pas aux yeux, mais avec un peu de jugeotte on pouvait s'en apercevoir (ce n'est pas pour rien qu'on appelle ce genre de jeux des casse-tête).

Si quelqu'un n'a pas compris jusqu'ici, qu'il n'hésite pas à se manifester... et si quelqu'un a compris jusqu'ici, qu'il n'hésite pas à essayer de pousser la réflexion plus loin: où jouer l'antépénultième coup? Et le précédent? Et celui encore avant? Et encore? Et encore?

Eh bien, c'est vraiment pas bien malin. Si on veut faire grossir par deux coups gagnants l'amorce de cavexe décrite sur l'image précédente, il n'y a pas de choix: un coup sur 13, un coup sur 37:



Il suffit de cliquer sur 3 ou 26 pour obtenir un cavexe très utilisable, mais pour une fois, allons donc un peu au-delà (sur l'image ci-dessous, nous n'avons plus un cavexe, mais une concavité):



Et si l'on essayait d'aller encore au-delà? Aussi loin que possible? Il suffirait de cliquer sur 11, 25, 36, 16 pour aboutir à une toute petite concavité de huit cases (un quadrilatère et un hexagone mariés):



Huit cases, ce n'est pas beaucoup, mais c'est suffisant pour commencer. Allez, lancez-vous, videz-moi cette grille avec la touche de magnétophone la plus à gauche, puis débrouillez-vous pour me prendre ces huit cases noires par deux coups bleus (deux cases isolées) et deux coups jaunes (deux fois des prises de trois cases). Cela fait, vous n'aurez plus qu'à reprendre à l'envers la séquence de coups employée pour faire grossir le cavexe, et zou, ça vous fera une grille résolue: deux cases isolées bleues, onze coups gagnants jaunes, et un pentagone final bleu. C'est vraiment fastoche, lancez-vous!

Bon, je vous ai tellement mâché le travail que je doute qu'il me reste grand chose à vous apprendre, mais voici quand même la solution la plus naturelle pour atteindre l'optimum sur la grille "pompidou" (des variantes sont bien sûr possibles, mais elles seront assez minimes):

21 30 (cases bleues isolées), 28 23 (fin de la petite concavité), 36 16 25 11 (fin de la grande concavité), 3 26 (le cavexe est désormais entamé), 37 13 (reste plus que les deux pentagones), 39 (onzième et dernier coup gagnant), 14 (ou autre chose, le dernier coup étant, comme presque toujours, indifférent: prise du pentagone final, en bleu).




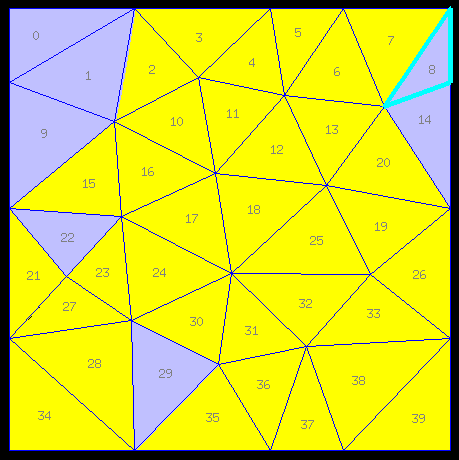
J'espère que vous avez compris... Dans le cas contraire, insistez: c'est vraiment un exemple très pédagogique, du fait qu'il ne tolère pas une multitude de variantes: à chaque stade de l'histoire, il y a très peu ou pas du tout de choix, donc le bon coup à jouer tombe sous le sens.

Je pourrais continuer à étudier mon inventaire dans l'ordre, mais j'ai envie de changer un peu, donc le problème du jour sera la grille "mercredi".



Tiens, un "trilatère": les cases 6, 7 et 8, réunies autour d'un sommet commun, dessinent donc à elle trois un triangle qui les englobe. C'est rare, mais ça ne doit pas vous inquiéter, il vous suffira de prendre ce "trilatère" convexe en un seul coup gagnant.

Je vous ai noté cette grille comme étant de difficulté moyenne... C'est vrai pour un joueur expérimenté comme celui que je me flatte d'être, car si vous regardez bien, il y a un cavexe vraiment facile. Mais il y a quand même aussi deux quadrilatères (3, 4, 5, 12 en haut, 27, 28, 29, 36 à droite) dont vous devrez vous dépatouiller, et ça, c'est généralement une vraie difficulté (je vous l'ai déjà dit un certain nombre de fois, on reconnaît un bon joueur de Triancey à sa façon de se débarrasser des quadrilatères). En l'occurrence, avec le cavexe qui va bien, on peut se débarrasser de ces deux quadrilatères dès le début et d'une façon assez enfantine... pour un joueur expérimenté. Pour des débutants, en revanche, ça risque de vous paraître assez coton.

Bon, essayez déjà de trouver le cavexe qui va bien, et si vous y parvenez, signalez-le, ce sera déjà un excellent début. Si vous n'y arrivez pas, je vous donnerai un coup de main un peu plus tard dans la journée.

Voici deux cavexes que je préconise pour la résolution de la grille "mercredi":



Le premier est le meilleur et le plus évident, je l'ai trouvé tout seul avec mon petit cerveau. C'est facile avec un peu d'entraînement, une fois qu'on a compris qu'en l'occurrence il faut jouer le dernier coup de la partie sur un hexagone (aujourd'hui, je ne vous en réexplique pas une énième fois la raison, j'ai la flemme, mais c'est comme toujours en rapport avec le nombre de cases).

Le deuxième cavexe a été trouvé par mon solveur, et j'en apprécie l'élégance: au lieu que le "trilatère" constitue une simple bizarrerie de la grille, il devient dans ce cavexe un élément essentiel de la solution et cela témoigne donc d'une certaine virtuosité. Bravo le solveur!

Solutions complètes en fin de journée.

Oh, mais c'est que je suis en train de vous oublier, moi...

Solutions:

Vous vous en êtes peut-être rendu compte, il y a deux jours, j'ai traité la grille "mercredi" avec une désinvolture dont je ne suis pas coutumier. C'est que j'étais en train de réfléchir à autre chose...

Cette grille était particulière en raison de deux circonstances qui vous ont probablement échappé, car elles n'étaient d'aucune pertinence pour la résolution de la grille; en revanche, elles ont titillé mes cellules grises surentraînées pour ce type d'exercices. Cette grille comportait en effet un "trilatère" (les cases 6, 7 et 8, rassemblées autour d'un sommet commun et constituant donc à elles trois un quatrième triangle) et aussi un quadrilatère marié à un pentagone (le quadrilatère 27, 28, 29 et 36, marié par 27 et 36 au pentagone 26, 27, 34, 35, 36), seule configuration permettant d'entamer une série de coups gagnants en sacrifiant une seule case bleue au lieu de deux comme d'ordinaire.

En l'occurrence, ces deux circonstances particulières ne changeaient rien. Mais le fait qu'elles soient réunies dans une seule grille m'a convaincu qu'il était temps pour moi de m'attaquer au Saint-Graal du joueur de Triancey "partrois"...



(Le Saint-Graal tel qu'imaginé par le peintre préraphaélite britannique Dante Gabriel Rossetti)

... la grille miraculeuse sur laquelle on peut atteindre l'archi-optimum théorique: toute la grille jaune (sauf la seule et unique case sur laquelle on doit jouer le premier coup: le théorème du premier coup est impitoyable).

La grille "mercredi" n'était pas ce Saint-Graal, mais elle lui ressemblait. Etait-il possible de la modifier légèrement pour la transformer en grille miraculeuse?


(si ça, c'est pas du teaser...)

Car oui, sur certaines grilles très rares, il est possible de commencer la série de coups gagnants (jaunes) en ne sacrifiant qu'une seule case (bleue). Et c'est le cas sur la grille "mercredi". L'image ci-dessous a été réalisée sans trucage (essayez-vous donc à la reconstituer, c'est très pédagogique):



Non, mais vous imaginez? Dix coups gagnants (jaunes) après un seul sacrifice (bleu)? Ah! Avouez que ça vous la coupe!

Mas si on peut, et je le prouve:

Et en plus, comme si ça ne suffisait pas, dans le couloir noir restant, on trouve le fameux trilatère (les cases 6, 7, 8 )... Oh, c'était clair, c'était un signe du destin, il fallait que je m'inspire de cette improbable grille "mercredi" pour fabriquer avec toute ma science algorithmique le Saint-Graal du joueur de Triancey partrois.

Quod feci, comme dit Arne Saknussemm dans Voyage au centre de la Terre.

Bravo ! J'avais bien vu qu'on pouvait terminer sur un trilatère, mais je pensais qu'on devait toujours sacrifier deux cases. Je n'avais pas pensé au coup du quadrilatère pour commencer.

Combien faudrait-il qu'il y ait de cases dans une grille Triancey "Saint-Graal", qu'on peut prendre entièrement "par trois" à l'exception d'une seule case? Eh bien, la réponse est pratiquement dans la question: ce nombre est forcément un multiple de trois majoré de 1 (eh!).

Mais nous savons par ailleurs que le nombre de cases d'une grille Triancey est toujours pair (si vous vous souvenez, nous en avons vu la démonstration dans un des épisodes précédents). Donc le nombre de cases d'une grille "Saint-Graal" doit être un multiple de trois impair majoré de un: ça pourrait être 34, 40, 46, 52 ou 58 (ces valeurs sont toujours séparées par 2 x 3 = 6 cases), mais certainement pas 44 comme dans la grille "mercredi".

Nous savons par ailleurs (l'avons-nous démontré? je ne sais plus, mais en tout cas c'est vrai) que le nombre de cases est toujours le double du nombre de sommets (étant entendu, bien sûr, que nous comptons les sommets sur le tore et non sur sa représentation plate et carrée). Si donc nous modifions la grille "mercredi", de 44 cases, pour la transformer en Saint-Graal, il faudra lui enlever deux sommets (et donc quatre cases), ou lui en ajouter un (et donc deux cases), ou encore lui en ajouter la bagatelle de quatre (et donc huit cases), voire sept (et donc quatorze cases).

Peste. Si j'avais fait ce calcul avant, je ne sais pas si j'aurais eu le courage de m'y essayer... Car la solution que j'ai trouvée, et que je finirai par vous montrer, comporte en effet 58 cases. Mais avant d'y arriver, j'ai fait un paquet d'essais (tous infructueux) avec 40, 46 et 52 cases. Peut-être m'y suis-je mal pris... En tout cas, je ne me serais pas cru si courageux. Maintenant je comprends mieux pourquoi ça m'a pris deux jours...

La question du nombre de cases du Saint-Graal étant résolue, il restait à trouver un moyen de dessiner un cavexe voué à s'achever sur un trilatère -- et donc, il fallait classiquement s'interroger sur l'avant-dernier coup, puis l'antépénultième, et chercher s'il était possible d'ajouter ce genre de configuration sur la grille "mercredi" sans trop en bouleverser l'aspect. Le plus simple m'a paru de marier mon trilatère final à un pentagone, conformément au théorème de l'avant-dernier coup dont je ne soulignerai jamais assez l'importance. Mais ça nous aurait donné quelque chose de ce genre...



... et je n'ai pas vu de moyen de faire apparaître une telle configuration dans la grille "mercredi" sans la chambouler profondément. En plus, l'aspect carré de l'espace réservé aux deux derniers coups me mettait mal à l'aise: pour bien réussir un cavexe, il faut rechercher des formes rondouillardes. J'ai donc pris la liberté d'imaginer mon cavexe non pas avec un trilatère, mais avec deux trilatères voisins, situation ultra-invraisemblable avec mes algorithmes de fabrication de grille, mais très facile à mettre en place (n'importe quelle case pouvant devenir un trilatère si on ajoute un sommet en plein milieu):



Cela nous fait une configuration rondouillarde de bon aloi. En outre, la grille "mercredi" comportait déjà un couple de pentagones (0,1, 2, 9, 10, marié à 0, 9, 17, 15, 16 par les cases 0 et 9), et ce couple était même idéalement placé hors de la zone où la présence du quadrilatère marié à un pentagone (27, 28, 29, 36 marié à 26, 27, 34, 35, 36) permettait d'espérer jouer les premiers coups en ne sacrifiant qu'une case bleue, comme nous l'avons vu ce matin.

Donc, il n'y avait en théorie plus qu'à trifouiller un peu la figure aux environs de son coin supérieur gauche pour réussir à la transformer en Saint-Graal. Ça n'allait pas forcément être simple, mais ça avait l'air possible.

Ouais, ben ça a pas été simple.

Il faut dire que si je me suis concocté de petits outils (des moulinettes Python, pour l'essentiel) assez efficaces pour produire et résoudre des multitudes de grilles, je n'ai rien prévu pour modifier une grille existante. Enfin, si, j'ai bien une possibilité à ma disposition, mais alors c'est hyper-basique: je peux éditer à la mimine les longues séries de nombres qui décrivent une de mes grilles dans une jolie syntaxe SGML simplifiée que j'ai définie moi-même et que donc je comprends, mais qui n'est quand même pas super-lisible, jugez-en:



Les coordonnées x et y, ça va encore, je peux vaguement évaluer où chacun des sommets se situe. En revanche, quand les sommets ou les cases sont désignés par de simples numéros attribués dans l'ordre de la création de ces petits bazars mathématiques, ben si je veux y comprendre quelque chose j'ai intérêt à me concocter des petits schémas explicatifs avant d'essayer de modifier ça à la mimine... et je vous garantis que ça n'est pas de la tarte. Enfin, ce n'est pas vraiment difficile, mais alors c'est d'un long et d'un fastidieux!



(Ci-dessus: quelques-uns des schémas qui m'ont servi à concocter mes brouillons; tous retravaillés à la souris, avec Gimp, le bon vieux logiciel de retouche du projet GNU -- le Photoshop du pauvre, quoi)

Eh bien j'ai quand même réussi à concocter ma grille miraculeuse rien qu'en modifiant de ci de là des mentions dans les descriptifs numériques de la grille "mercredi", et j'ai fait tout ça avec un bête éditeur de texte (bon, d'accord, un bon éditeur de texte: emacs). Je suis quand même un gars un peu bizarre: j'arrive sans grande peine à m'astreindre à faire des trucs qui seraient jugés insupportablement galères par un bénédictin sous tranquillisants. Pensez-vous que je devrais voir un psy?

Petitagore a écrit:Pensez-vous que je devrais voir un psy?

Surtout pas !

Je vais finir par vous la montrer, ma grille miracle, mais je tenais à profiter de l'occasion pour vous parler un peu de la cuisine informatique de fabrication de toutes ces petites merveilles. Si vous êtes profanes, cela vous inspirera peut-être une terreur sacrée et déclenchera chez vous une rechute de ce syndrome de l'imposteur que subit toujours peu ou prou, paraît-il, tout surdoué inopinément confronté à d'autres surdoués, par exemple lors d'une première rencontre avec les membres de Mensa: oh la la, tous les autres sont super-intelligents, je comprends absolument rien à ce qu'ils racontent, qu'est-ce qu'ils m'impressionnent et me sont supérieurs, si j'ai été admis parmi eux c'est évidemment que mon dossier a été mélangé avec quelqu'un de vraiment intelligent mais moi j'ai rien à fiche parmi eux et je vais m'éclipser discrètement avant de m'être ridiculisé.

J'aime bien inspirer ce genre de terreur sacrée. D'autant plus que je l'ai déjà ressentie bien des fois moi-même.

Si en revanche, au lieu d'être profanes, vous êtes de vieux informaticiens blanchis sous le harnais et connaissant bien cette vieille merveille qu'est Unix-Linux, je pense que l'écran suivant a tout pour déclencher votre hilarité...



... tellement une telle façon de travailler est élémentaire, vieillotte, ringarde et obsolète. Il s'agit de mes deux scripts principaux, portant les noms poétiques de yo et vazy (vazy fait l'essentiel du boulot, mais hiérarchiquement parlant il dépend de yo qui l'appelle). Quand j'ai envie de me faire une grille Triancey, par exemple aujourd'hui une grille que je pourrais appeler poétiquement "20150411", ben je n'ai qu'à taper yo 20150411 (bon, en fait c'est ./yo.sh 20150411, mais là je simplifie pour les béotiens), et zou, ça enclenche le processus automagique:

- ça saupoudre des points pseudo-aléatoires sur la grille (script reseau_de_points);

- ça trace des segments entre les points (script de_pts_a_segm);

- ça assemble ces segments trois par trois pour créer des triangles (script de_segm_a_tri);

- ah, ça c'est très joli et j'en suis super-fier: ça déplace légèrement les sommets pour arrondir les angles et éviter les triangles trop effilés (script adoube_points; "adouber", aux échecs, c'est replacer une pièce au milieu de sa case);

- ça renumérote les triangles de gauche à droite et de haut en bas (script renumerote_triangles) pour qu'on s'y retrouve un peu quand la grille est affichée...

- ... mais aussitôt ça les rerenumérote en les mélangeant (script brasse_triangles) pour que le solveur ait besoin de se creuser la tête au lieu de toujours me filer des solutions s'achevant à proximité du coin inférieur gauche, ce à quoi son tempérament psycho-rigide le mènerait toujours si je le laissais faire;

- et zou, ça m'affiche la grille dans une interface clicable (script triancey.py), mais au préalable ça a noté quelque part la solution préconisée par le solveur, au cas où je n'y arriverais pas tout seul.

Et ouais, ça fait tout ça rien que quand je tape "yo". C'est l'ambiance: Dieu dit "que la lumière soit" et la lumière fut. Eh bien, avant d'en arriver là, croyez-moi, Dieu il a au minimum sacrément prémâché le boulot dans plein de petits scripts Python.

A l'époque héroîque, les unixiens appelaient cette façon de travailler KISS pour Keep It Small and Simple: pour faciliter le débogage, au lieu de concevoir un très très gros logiciel qui fait tout, on faisait plein de petits morceaux débogables individuellement, et notant systématiquement leurs résultats dans des petits fichiers de texte (ici, les fichiers dont le nom se termine par .sgml; ce sont ces fichiers que j'ai modifiés à la main pour aboutir à ma grille miracle). Ça marchait très bien, d'ailleurs ça marche toujours très bien, la preuve, mais ça fait ringard et obsolète, et employer cette technique c'est un peu comme d'aller aux putes dans la société victorienne: ce sont des choses qu'à l'occasion un gentleman peut faire, mais dont en aucune circonstance il ne devrait parler because it's shocking, vulgaire, plébéien. D'ailleurs avez-vous jamais entendu le Bon Dieu vous raconter comment il a écrit des scripts Python avant de dire Fiat Lux? Ben non. Ce qui vous prouve bien que le Bon Dieu est un gentleman, lui.

Ben moi je suis un prolo mal élevé, c'est comme ça que je travaille et je vous merde tous, na.

Bon, allez-je vous ai assez fait languir. La voici, cette incroyable et miraculeuse grille "saint Graal":



Vous noterez que je ne vous ai pas menti, il s'agit bien d'une modification de la grille "mercredi" que nous avons déjà étudiée.

Cette grille-saint Graal peut être intégralement prise en jaune, à la seule exception de la première case sur laquelle vous cliquerez. Cinquante-huit cases, un premier coup perdant prenant une case isolée (bleue), suivi de 19 coups gagnants prenant en jaune les 57 cases restantes. Voilà un exploit tel que seuls de preux chevaliers sont dignes d'en rêver.

Pour cette grille exceptionnelle et miraculeuse, je ne vous indiquerai point de solution. Si vous la trouvez par votre seule vertu, il est légitime que vous en tiriez gloire. Envoyez-moi donc la solution en MP et je confirmerai que vous ne fanfaronnez pas. Mais cela dit, gardez le secret: cette grille doit rester un objet cryptique et ésotérique, sous peine de déclencher l'ire redoutable des forces mystérieuses de la logique et de l'arithmétique. Ces dernières ne manqueraient point de déchaîner immédiatement leur fureur sur l'impudent mortel qui aurait la folie de révéler un aussi puissant secret.

La grille "Saint-Graal", parfaite comme elle est, ferait une bonne conclusion à la saga des grilles Triancey, et c'est probablement ainsi que je l'utiliserai si je mène à son terme le projet d'aboutir un jour à une monographie sur mon petit casse-tête, mais je vais sans doute continuer à alimenter ce fil au moins un certain temps, quand ce ne serait que pour venir à bout de mon inventaire, où il serait fort frustrant que je négligeasse les grilles données comme difficiles ou particulières.

Dans l'immédiat, je vais terminer l'étude systématique des grilles de difficulté moyenne, et vu quel jour nous sommes, le problème du jour sera la grille "mardi",.



C'est une grille assez normale, à part qu'elle n'a que 36 cases, ce qui est relativement peu. Ça ne modifie pas fondamentalement l'exercice, et je vous recommande de partir aussitôt à la chasse au cavexe, comme expliqué dans les épisodes précédents (tout particulièrement celui-ci, dont je recommande à ceux qui arrivent sur ce fil de se taper au plus vite la lecture attentive, parce que quand je fais des efforts pédagogiques, c'est pour que ça serve).

Et pendant que vous réfléchissez, je vais peut-être vous intercaler un petit délire métaphysique bien dans ma manière à partir d'une comparaison entre les grilles "mercredi" et "Saint-Graal" que nous venons d'étudier et qui, comme nous l'avons vu, sont apparentées vu que la seconde est une modification de la première (essayez de suivre, quoi!).

Allez, un petit délire métaphysique pour ne pas perdre la main.

Nous avons vu que la grille Saint-Graal est la grille parfaite, celle qu'on peut prendre intégralement en jaune sauf la première case sur laquelle on clique. Sur cette grille archangélique, l'optimum est donc égal au nombre de cases minoré de seulement 1 -- alors que dans l'immense majorité des autres cas que nous avons étudiés, il fallait sacrifier 2 + 5, 2 + 6 ou 2 + 7 cases, berk berk berk, comme nous étions alors loin de l'idéal théorique et de la perfection divine.

Et pourtant, cette merveilleuse et extraordinaire grille "Saint-Graal" garde très nettement un grand nombre de caractéristiques héritées du modèle qui l'a inspirée, la grille "mercredi" (comparez les deux figures si vous ne me croyez pas).



(Sur l'image ci-dessus, les traits bleus représentent la grille "Saint-Graal", les traits verts la grille "mercredi")

En quelque sorte, la grille "mercredi" a été transfigurée, elle a connu la rédemption, elle est passée d'une imperfection toute terrestre à une pureté archangélique, et on voit là sans l'ombre d'un doute l'intervention de l'omniscience divine.

(Ah bon, vous, vous ne la voyez pas? Quel dommage pour vous, ça prouve que vous n'avez vraiment pas le tempérament mystique...)

Bon, d'accord, ce n'est pas de l'omniscience divine, c'est seulement de l'intelligence humaine, la mienne en l'occurrence: en m'inspirant de cette grille "mercredi" qui était pleine de défauts comme toutes les grilles car conçue par un simple automatisme pseudo-aléatoire, j'ai élaboré la grille parfaite, et je l'ai fait avec mes petites cellules grises, en témoignant ainsi de ma maîtrise totale du problème (de mon omniscience, quoi). Je ne suis pas Dieu, mais j'ose dire en toute modestie que Dieu en personne n'aurait pas fait mieux, because l'optimum c'est l'optimum, pour un Dieu hypothétique comme pour moi: la grille "Saint-Graal" est indépassable, elle est d'une splendeur divine, parfaitement.

C'est qu'en effet l'homme, tout imparfait, fini et mortel qu'il est, parvient parfois à s'élever au niveau du divin, et alors ça donne... des trucs super, vraiment; la toccata et fugue de Jean-Sébastien, le Taj-Mahal, la Liberté guidant le peuple de Delacroix, le concerto pour violon de Mendelssohn (surtout joué par Sayaka Shoji)... ou encore l'incomparable grille "saint-Graal" de Petitagore: vraiment y a pas mieux, c'est tellement beau qu'on a envie de se mettre à genoux devant, et toutes ces oeuvres insurpassables témoignent de ce que l'humain a du divin en lui, sacré nom de Dieu!

(non, c'est pas un gros mot, encore moins du blasphème: c'est de l'exaltation mystique tout ce qu'il y a de plus légitime; frères athées, cherchez pas, vous pouvez pas comprendre)

Et maintenant que j'ai ainsi démontré que je touche au divin, moi qui suis le seul et unique Créateur de toutes les grilles Triancey connues à ce jour, moi qui suis donc, dans le petit monde mathématique de mes grilles, le représentant légitime et incontestable de Dieu en personne, parfait, omniscient et bienveillant...

... eh bien je me pose la question que tout Dieu qui se respecte ne peut manquer de se poser:

(vraiment, vous ne voyez pas? mais c'est terrible d'être terre-à-terre à ce point...)

Cette question, la voici: de ces deux créatures qui sont miennes, la grille archangélique "Saint-Graal" et la grille bassement terrestre "mercredi" -- laquelle a le plus vocation à s'attirer mes sentiments d'amour et d'infinie miséricorde? Ou, plus platement, à m'inciter à me triturer les neurones dessus?

(Vraiment, vous n'auriez pas pensé à vous poser cette question? Ah, vous me décevez, c'est terrible de manquer de tempérament mystique à ce point... Mais à défaut d'avoir eu l'idée de poser la question, saurez-vous me donner la réponse? Quelle est la grille que je préfère? La grille irréprochable "Saint-Graal", ou la médiocre et terrestre grille "mercredi" qui l'a inspirée?)

Encore raté! Mais non, ce n'est pas la grille Saint-Graal qui s'attire ma faveur divine. Bien au contraire elle me déplaît souverainement, la grille Saint-Graal, avec sa petite gueule d'ange et de premier de la classe. Elle ne présente aucun intérêt, cette grille à la con, j'ai su avant même de la fabriquer comment j'allais ensuite la résoudre, c'est un cas d'école, elle n'a pas sa place dans la vraie vie -- et puis j'ai jamais aimé les fayots, d'abord.

Mais il y a bien plus grave.

Vous avez vu que cette foutue grille "Saint-Graal", elle m'a demandé deux jours de travail! Alors que n'importe quelle grille "bassement terrestre" du type de celles que je vous ai présentées dans ce passionnant feuilleton peut être créée par mes petites moulinettes Python en moins de quinze secondes! Donc, dans le même temps qu'il me faut pour fabriquer une seule grille "Saint-Graal", j'aurais pu fabriquer... plus de cinq mille grilles imparfaites.

A votre avis, comment un Dieu omniscient qui se respecte décide-t-il d'employer son éternité une fois qu'il a fait une constatation de ce genre? Vais-je préférer une demi-douzaine de grilles aussi irréprochables qu'ennuyeuses, et qui me demanderaient des semaines d'un travail éreintant, ou la multitude innombrable des grilles imparfaites mais passionnantes que peuvent créer sans jamais se lasser mes moulinettes Python?

Eh bien pareillement, pensez-vous que le Bon Dieu préfère passer l'éternité en compagnie d'une toute petite troupe d'archanges créés à grand ahan et peine en Dieu sait combien de myriades d'éons, ou bien d'une innombrable multitude de pécheurs certes bourrés de défauts, mais que l'on peut créer en un tournemain (ça prend neuf mois en général, à comparer aux milliards d'années de l'univers), et en quantité industrielle, rien qu'en laissant tourner les automatismes de l'évolution?

Et par là-même nous comprenons pourquoi le Bon Dieu, qui dans son jeune temps a paraît-il créé un paquet de fayots et de premiers de la classe qu'on appelle ses anges, s'est très vite désintéressé de cette bande de connards irréprochables pour créer une multitude d'humains inférieurs, médiocres, méchants, égoïstes, mesquins, minables -- mais avec lesquels la recherche d'un optimum moral est stimulante pour l'esprit du Très-Haut. Chaque mortel est en quelque sorte une grille Triancey, bourrée de péchés, de quadrilatères qui font tout foirer, et le développement moral d'un pécheur correspond à l'identification (par le dit pécheur ou par le Bon Dieu lui-même, selon les cas) du cavexe qui permet d'atteindre en sa grille-âme l'optimum moral dont il est capable.

En fait, chaque être humain immonde et mesquin est pour le Bon Dieu... une espèce de casse-tête exaspérant (mais passionnant!) -- exactement de la même façon que chaque grille Triancey est un casse-tête exaspérant mais passionnant pour le joueur humain qui s'y attaque.

Quiconque résoud une grille Triancey sauve en quelque sorte l'âme mathématique de cette grille. Puisse le Très-Haut résoudre pareillement et au plus vite les défis moraux de nos turpitudes!

(et surtout puisse-t-il mettre très vite au point un solveur adapté aux circonvolutions de nos âmes, parce que là, en ce moment, sur notre petite planète polluée, je trouve qu'on est encore vraiment très très loin de l'optimum)

Je connais de sales flemmards qui préféreraient que le Bon Dieu fasse tout le boulot, qu'il les fasse "naître de nouveau", qu'il débogue leur âme en quelque sorte, pour que leurs faiblesses morales fassent place à une configuration parfaite, nickel-chrome, incapable de la moindre vilenie; qu'ils deviennent des anges, quoi.

Je ne dis pas que le Bon Dieu n'est pas capable de se créer des anges irréprochables, de même que je vous ai montré que j'étais capable de concevoir l'irréprochable grille "Saint-Graal". D'ailleurs, si j'ai bien appris ce qu'on m'a dit au caté, il paraît qu'il a déjà fait le coup: je te prends Saul, l'infect lapideur de chrétiens, sur le chemin de Damas, et hop, shazam! je te lui transforme l'âme du tout au tout comme ça, schlak; et voilà un petit saint Paul bien propre pour le panthéon chrétien. Certes, il ne le méritait aucunement, mais ça fait rien c'était faisable, Dieu est miséricordieux, et il s'est amusé à lui déboguer l'âme, comme ça, sans vraie raison, parce qu'il a remarqué dans son âme des particularités bizarroïdes, tout comme j'avais remarqué dans la grille "mercredi" un trilatère très inhabituel, ainsi qu'un non moins inhabituel quadrilatère marié à un pentagone... Alors, pour la beauté du geste et le défi intellectuel, allez, moi Petitagore je vous montre que je peux concocter une grille "Saint-Graal", et pareillement le Très-Haut a parfois la lubie de montrer qu'il est vraiment le Bon Dieu, allez, pof, ce gros connard de lapideur, je vous en fais un saint canonisé; c'est pas vraiment utile mais bon, je suis un super-pro et j'avais envie de vous le montrer. De temps en temps, pour le pur plaisir intellectuel, Dieu peut perdre un peu de son éternité à transfigurer consciencieusement une âme qui n'en vaut pas la peine, de même que moi je peux consacrer deux journées de chômedu à me lancer un défi intellectuel complètement inutile. Lui comme moi, nous pouvons le faire, et c'est à ça qu'on reconnaît que nous sommes vraiment des pros.



(Ci-dessus: la Conversion de Saint Paul telle qu'imaginée par Le Caravage)

Je ne critique pas, ce serait blasphématoire, mais tout de même, quel ennui (lisez les épîtres du dit saint Paul si vous ne me croyez pas: ça valait bien la peine de lui sauver son âme, à ce connard: tout ce qu'il y écrit est prêchi-prêcha et bêtassou à mourir). Tandis que gagner son paradis sans rien perdre de sa nature de misérable pécheur imparfait et médiocre, ça c'est un défi moral intéressant! Maîtriser son agressivité, sa cupidité, son égoïsme, ses appétits grossiers, sa vanité, son hypocrisie, sa vilenie, voire sa libido si vraiment on y tient, pour réussir au bout de longues décennies et après moult essais infructueux à devenir... un type toujours absolument ordinaire et quelconque, mais quand même un vrai brave type... moi je dis qu'aux yeux du Bon Dieu c'est autrement plus intéressant.

Bref, aux chiottes les anges et les saints canonisés, vive les pécheurs imparfaits, et au diable les grilles Triancey irréprochables, vive la recherche de l'optimum sur les médiocres grilles qu'engendre ce bon vieux hasard.

Bon, alors, voici de bons cavexes pour résoudre la grille "mardi" -- laquelle, ayant 36 cases, ne saurait atteindre un score optimal qu'en s'achevant sur un heptagone marié à un pentagone, comme il a été maintes fois expliqué lors des épisodes précédents.

Voici deux cavexes assez simples d'emploi (d'ailleurs on peut considérer que ce sont deux variantes de la même idée):



Mon solveur en a trouvé deux autres moins concis mais utilisables et en plus assez faciles à photographier mentalement, coincés qu'ils sont contre le bord supérieur:



Par contre, j'espère que vous n'avez pas comme moi perdu un temps interminable à vous échiner sur ce cavexe-là:



Ce n'était pourtant pas idiot de remarquer la présence d'un heptagone autour des quatre coins du tore... mais j'ai eu beau faire, je ne suis pas parvenu à trouver une solution optimale utilisant ce cavexe, et mon solveur que j'ai pas mal sollicité n'y a jamais recours non plus, ça doit donc être impossible.

Solutions complètes en fin de soirée si je n'oublie pas.

Et voici donc comme promis les solutions complètes pour la grille "mardi":

Solutions complètes:

C'est drôle, même quand je n'écris rien sur ce fil je vois son compteur qui s'incrémente... Il y a eu dans les 150 consultations depuis avant-hier, mais comme personne n'écrit rien ici ni ne m'envoie de message personnel, je ne sais pas du tout si ce sont 150 internautes qui ont juste cliqué et sont tous repartis une demi-seconde après en constatant que ça ne les intéressait pas (ça me vexerait mais ce serait quand même leur droit le plus strict) ou au contraire un seul matheux motivé qui s'est tapé vingt fois de suite la lecture ultra-attentive des neuf pages qui précèdent... C'est probablement quelque part entre les deux, mais je n'ai aucun moyen de le savoir. Réagissez, les gars! Moi, je ne demande qu'à adapter mon discours aux desiderata de ceux qui me lisent, mais faudrait déjà que ces desiderata soient exprimés...

En attendant, comme je tiens à venir à bout des trente-quatre grilles que j'ai mises à votre disposition (c'est une sélection arbitraire, je pourrais en fabriquer sans peine des dizaines de milliers d'autres), il faut aussi que je touche un mot des grilles pas très intéressantes et pas très pédagogiques qui se trouvent dans ce lot. C'est le cas de la grille "giscard" dont je vais vous entretenir aujourd'hui:



Je n'ai aucun grief (enfin, aucun à développer ici) contre le président Giscard d'Estaing, mais le fait est que cette grille "giscard" est vraiment une des moins intéressantes du lot. Ca ne veut pas dire qu'on ne peut rien faire du tout avec elle (toutes les grilles ont un optimum, donc c'est toujours un défi que de l'atteindre; simplement, ce défi est plus ou moins motivant, et aujourd'hui il ne l'est pas beaucoup), mais je ne veux pas être sadique avec vous et je tue tout de suite le suspense: sur cette grille, l'optimum est de dix coups gagnants (jaunes) et non onze comme on pourrait légitimement le croire. Or réussir dix coups gagnants sur cette grille est vraiment assez facile pour quelqu'un d'un peu entraîné -- de sorte que si je ne vous prévenais pas vous penseriez probablement qu'il faut essayer de faire mieux. Eh bien, ce n'est pas la peine de chercher à attraper un chat noir dans cette pièce sombre: il n'y est pas, vous perdriez votre temps.

C'est ce que j'appelle une grille "cinq ou huit", et ces grilles sont tantôt beaucoup plus simples, tantôt beaucoup plus compliquées que les autres, et le malheur est qu'il n'y a à ma connaissance aucun moyen humain de le savoir a priori. Avec ces grilles heureusement assez atypiques et peu courantes, seul un solveur informatique peut vous dire à l'avance: "Mon gars, te casse pas la nénette à essayer de faire onze coups gagnants, c'est perdu d'avance; fais en dix en aussi peu de temps que possible, et tout de suite après attaque une autre grille." Au contraire, sur des grilles qui n'ont pas du tout l'air différentes a priori, ce même solveur est susceptible de vous dire: "Eh bien si, même si ça fait déjà trois heures que tu te casses les dents dessus, on peut faire onze coups gagnants sur cette grille, c'est effroyablement difficile mais pas impossible, alors accroche-toi..." et dans ces cas-là, il arrive non seulement que l'humain puisse trouver une solution mais qu'en plus ça lui procure la satisfaction fort légitime d'avoir accompli un exploit.

Hélas, au moment où on se présente devant la grille sans rien savoir sur elle, impossible de dire a priori si ça va être une petite promenade en montagne à vache avec impossibilité de faire mieux, ou l'escalade de la face nord des Grandes Jorasses avec toute la gloire et le prestige qui vont avec.

C'est pour ça qu'aujourd'hui je tue le suspense. J'ai peut-être tort, car ces grilles "cinq ou huit" sont de belles écoles de courage, et on peut faire de grands progrès en s'acharnant sur elles, en envisageant avec elles les hypothèses les plus tordues et les plus emberlificotées -- y compris, comme aujourd'hui, quand ça ne peut servir à rien. Celui qui ne s'est jamais escrimé sur une grille impossible a peu de chances de réussir jamais une grille "seulement" très difficile... et donc les efforts inutiles sont en fait très utiles! Mais la lutte contre l'impossible n'est pas un exercice à recommander aux débutants (c'est trop décourageant), donc je vous en dispense. Aujourd'hui du moins.

Or donc, la grille "giscard" est l'occasion d'une bête promenade de santé avec dix coups gagnants seulement, et il n'y a pas la moindre chance de réussir sur elle un exploit à noter dans les annales. Ne vous cassez pas la nénette, allez au plus simple.

En revanche, si vous n'arrivez pas à me faire dix coups gagnants sur cette grille... oh, ben là ça veut dire qu'il faut que vous étudiiez mieux les chapitres précédents!

Bon, alors, finissons-en avec la grille "giscard".

Ça n'a vraiment pas grand rapport, mais ça me rappelle l'excellente blague d'André Santini, le maire d'Issy-les-Moulineaux et d'ailleurs ancien giscardien lui-même, au lendemain des obsèques quasi-nationales de Mitterrand:

-- Elles étaient vraiment superbes, les obsèques de Mitterrand. C'est vraiment dommage qu'on n'ait pas fait les mêmes pour Giscard.

Giscard, à ce qu'on dit, l'avait très mal pris -- et du coup c'est encore plus drôle!

Bon, ben toujours est-il que la grille "giscard", elle, elle n'est pas drôle du tout. Elle a quarante cases, donc si on en sacrifie deux au départ comme il est presque toujours nécessaire, il en reste 38, soit un multiple de trois majoré de deux -- donc pour atteindre un score optimal il faudra prendre au dernier coup un nombre de cases égal à un multiple de trois majoré de deux, idéalement un pentagone. Et en vertu du théorème de l'avant-dernier coup, qui dit que l'avant-dernier coup d'une partie à score optimal "classique" doit être joué sur un pentagone, nous sommes donc à la recherche d'un couple de pentagones pour terminer la résolution de cette grille sur le score optimal théorique.

Il n'y a qu'un couple de pentagones et un seul sur cette grille, collé contre le milieu du bord droit: les cases 16, 17, 18, 24, 25, 26, 27 et 31. On pourrait en théorie y jouer les deux derniers coups, et le coup précédent pourrait prendre les cases 11, 19 et 20 le long du bord gauche cette fois... Mais en deçà?

Ben en deçà, que pouic: je ne vois aucun moyen d'avoir un coup gagnant en amont de ces trois derniers coups optimaux théoriques.

Alors?

Ben alors c'est râpé: on ne va pas réussir le score optimal théorique, il faut donc revoir nos ambitions à la baisse et sacrifier au dernier coup non pas les cinq cases d'un pentagone, mais 5 + 3, soit huit cases.

Le moyen le plus simple de prendre huit cases au dernier coup est en général de prendre un couloir de huit cases. Sur cette grille, il y a deux emplacements possibles: la rangée du haut (0, 1, 2, 3 , 4, 5, 10, 6) et... la rangée du bas (cases 32 à 39).

Bon, on peut le faire, mais c'est hyper-banal. Rien d'autre? Pas de possibilité de terminer sur un octogone? Ben non, vu que cette grille sans génie n'en comporte pas. Pas de possibilité de terminer sur deux quadrilatères? Ben non, vu qu'il n'y en a qu'un (les cases 9, 13, 14 et 15). Peut-on au moins terminer sur un hexagone marié à un quadrilatère par deux cases, ce qui nous ferait 6 + 4 - 2 cases communes = 8 cases? Ça paraît possible en ajoutant au quadrilatère que je viens de citer l'hexagone 12, 13, 14, 21, 22, 23... mais ça va être le même problème que pour le couple de pentagones: où trouver un coup gagner à jouer en amont de ce couple maudit? Nulle part.

Bon, ben décidément, va falloir terminer sur un couloir de huit cases. Mon Dieu que c'est pas rigolo.

Allez, visons le couloir du haut de la grille, et débarrassons-nous tout de suite de l'ennuyeux quadrilatère: 15, 11 (cases isolées, bleues), 13, 8, 17 (coups gagnants jaunes), et zou, voilà la deuxième rangée horizontale prise, avec le quadrilatère dedans, plus aucune difficulté en vue.

On continue sans se casser la nénette: 19, 26... mettons encore... 38... et puis... 23, 35, 29, 33. Et il n'y a plus qu'à cliquer sur n'importe quelle case restante.

Ça a été du massacre. A vaincre sans péril, on triomphe sans gloire.

Allez, c'est tellement pas drôle que je laisse le solveur se débrouiller pour terminer sur la rangée du bas de la grille: 3 6 5 1 11 13 19 29 14 18 26 30 34. Ouais, ça marche aussi, et ça n'est pas très inspiré non plus.

On va être gentils et dire que c'était une grille pour débutants!

Je ne veux pas vous faire prendre en grippe les grilles "cinq ou huit", donc aujourd'hui nous allons résoudre la grille "jeudi", très similaire à celle que nous avons vue hier (il faut également essayer de terminer sur un couple de pentagones), mais pas insoluble, cette fois:



Notez que c'est toujours beaucoup plus facile de trouver une solution quand on a la certitude qu'elle existe, car alors on a beaucoup moins d'efforts à faire pour lutter contre le découragement. Faute d'avoir cette certitude, on ne peut être sauvé que par une foi aveugle en la victoire... mais je ne suis pas un prêcheur évangéliste et je me garderai bien de vous présenter ça comme une méthode infaillible: quand bien même vous auriez une foi suffisante pour marcher sur les eaux (et vous me permettrez d'en douter), elle ne vous sera d'aucune utilité pour résoudre une grille insoluble. C'est ça qui est embêtant avec la foi: quand on n'en a pas alors qu'on s'attaque à un projet difficile comme la grille d'aujourd'hui, ça peut bel et bien être un inconvénient que d'en manquer; mais quand on en a à ne savoir qu'en faire et qu'on s'attaque à l'impossible comme à la grille d'hier... eh ben elle ne sert qu'à épuiser son énergie en vains efforts. Un bon prêcheur vous dirait sans doute que la foi ne vous dispense pas d'implorer l'aide de Dieu... et moi je vous dirai qu'elle ne vous dispense pas de réfléchir et de raisonner.

Toujours est-il que la grille "jeudi", elle, n'est pas insoluble. Croyez fermement en la victoire et vous la résoudrez, sinon vous vous enfoncerez dans les abîmes de perplexité et je vous dirai comme Jésus à saint Pierre: "Homme de peu de foi, pourquoi as-tu douté?"



(Saint Pierre tentant de marcher sur les eaux, par François Boucher)

Haut les coeurs, à l'attaque!

Il n'y a pas une foule de bons cavexes pour résoudre la grille "jeudi". Quand je fais plancher mon solveur, dessus, la plupart du temps il atteint l'optimum en employant des cavexes "à mortaise", non inversibles, du genre de celui-ci que je trouve assez ingénieux:



(N'oubliez pas que quand je cherche à vous décrire un cavexe "à mortaise", les cases jaunes représentent les premiers coups de la partie, au contraire de ce que je fais habituellement: d'ordinaire, sur l'image d'un cavexe, les cases colorées désignent la zone où il faudra jouer la fin de la partie et non pas son début. Je sais, tout cela est terriblement contre-intuitif... mais le caractère non inversible des cavexes "à mortaise" l'impose. Et puis, de toute façon, par nature un casse-tête n'est pas un truc intuitif, faudra vous y faire!)

Cela étant, il y a quand même quelques bons cavexes inversibles et rondouillards concevables, même s'ils ne brillent pas par la concision:



Il est peut-être possible d'en dessiner d'autres, mais ces quatre-là sont à l'heure où je vous parle les seuls dont je sois sûr qu'ils peuvent être employés pour atteindre l'optimum.

Solutions complètes dans la soirée, voire dans la nuit.

Avant de balancer les solutions complètes de la grille "jeudi", il faut que j'ajoute un dernier cavexe (appelons-le le cavexe 3) que mon solveur a imaginé entre-temps et qui est peut-être le meilleur du lot:



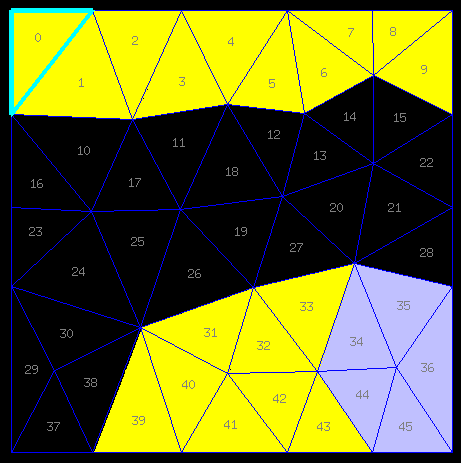
Et cette omission étant réparée...

... allons-y pour les solutions complètes:

Vous voyez que ç'aurait été bougrement dommage de déclarer cette grille insoluble, même si elle n'était pas vraiment simple.

Le problème du jour sera la grille "mitterrand".



Pour les gens de ma génération (j'avais vingt ans quand Mitterrand a été élu, et à ma courte honte je dois dire que j'ai voté pour lui, fait la fête à la Bastille et tout le toutim), il est tentant de faire une comparaison avec cette grille et la grille "giscard" que nous avons vue il y a peu. Les deux grilles ont d'ailleurs le même nombre de cases, donc les raisonnements arithmétiques qu'elles appellent toutes deux sont totalement similaires au départ.

Rappelons-les, la répétition étant la base même de la pédagogie...

Pour entamer la série ininterrompue de coups gagnants (jaunes) qui constitue l'objectif de ce jeu, il faut sauf exceptions rarissimes commencer par sacrifier deux cases isolées (bleues) sur toute grille à laquelle on s'attaque. Quarante cases moins deux sacrifiées au départ, reste trente-huit. Trente-huit n'est pas un multiple de trois, mais un multiple de trois majoré de deux (ou minoré de un, ça revient au même), donc le dernier coup joué sur ces trente-huit cases restantes ne pourra pas être un coup gagnant, il faudra qu'il prenne un nombre de cases qui soit lui-même un multiple de trois majoré de deux. La plus petite quantité envisageable répondant à cette condition étant de cinq cases, nous savons que nous devons chercher sur cette grille un pentagone sur lequel jouer le dernier coup.

Seulement, avant le dernier coup, il y a l'avant-dernier, et le très important théorème de l'avant-dernier coup a établi qu'on ne peut atteindre un score optimal "classique" que si l'avant-dernier coup est lui-même joué sur un pentagone situé à proximité immédiate du polygone final... Donc nous cherchons sur la grille "mitterrand" dont je viens de publier l'image la même configuration que sur la grille "giscard" que nous avons étudiée naguère: nous cherchons un couple de pentagones, c'est-à-dire deux pentagones "mariés", possédant deux cases en commun.

Eh bien, ne vous cassez pas la nénette: sur la grille "giscard", ça existait, mais dans la maison "mitterrand", il n'y a rien de tel (à l'époque le Parti socialiste n'était pas encore infesté de tarlouzes mais je raye tout de suite cette vanne idiote car l'humour homophobe n'est pas ma tasse de thé). Donc, ce n'est pas la peine de fantasmer sur le score optimal "classique" (deux cases bleues sacrifiées au départ, un pentagone à l'avant-dernier coup et le plus petit polygone convexe possible au dernier coup), on n'est pas dans la catégorie maudite des grilles "cinq ou huit" et il faut tout simplement prendre non pas cinq, mais bien 5 + 3 = huit cases au dernier coup. La grille "giscard" vous donnait de faux espoirs (de terminer sur un pentagone), la grille "mitterrand" douche carrément votre enthousiasme d'emblée (je ne suis pas sûr qu'historiquement ça se soit vraiment passé comme ça lors de l'élection de ces deux tristes sires, mais en ce qui concerne mes grilles, je vous assure que je ne vous dis pas de sottises).

Bon, ben voilà. Terminer sur huit cases, d'ordinaire, est assez facile, donc allez-y gaiement. Mais méfiez-vous quand même: Mitterrand était un roublard, et ceux qui pensaient se défaire de lui en six mois ont quand même dû se le coltiner pendant deux septennats... Pareillement, cette grille est peut-être moins simple qu'il n'y paraît.

Allez, quelques pistes pour résoudre la grille "mitterrand":



J'ai honte, mais je n'ai pas vu les deux couloirs parfaitement utilisables que mon solveur, lui, n'a bien sûr pas ratés; apparemment, je n'arrive pas toujours à compter jusqu'à huit. En revanche, j'ai trouvé sans tricher le premier cavexe (et la solution qui va avec). Si vous n'avez rien fait de tout ça, eh bien je ne vous félicite pas.

Solutions complètes avant demain si je n'oublie pas.

Voici donc les solutions complètes pour la grille "mitterrand".

Solutions complètes:

Et bonne nuit à tous.

Il fallait bien que ça arrive un jour (quelle idée idiote j'ai eue de donner des noms de présidents de la République à mes grilles), le problème du jour sera la grille "sarkozy".



Le personnage ne m'inspire vraiment pas grand-chose d'autre que "casse-toi pôv'con", comme il le dit lui-même avec ce style distingué, raffiné, spirituel, cultivé et intellectuel que nous lui connaissons tous et qui convient si bien à un successeur des rois de France.

Je m'empresse de dire que la grille est plus intéressante que le personnage: elle est plus complexe qu'elle ne paraît -- contrairement à lui, qui fait l'effet d'un inintéressant médiocre parce qu'il l'est bel et bien.

Si ces propos peu aimables (et absolument pas argumentés; j'assume, ça n'en vaut pas la peine) m'aliènent des lecteurs... ben je m'en consolerai. Je n'irai pas jusqu'à leur dire "cassez-vous pôv'cons", parce que je suis un peu plus raffiné que le personnage et que je suppose (philanthropiquement) que leur âme peut être plus complexe que leur bulletin de vote... mais bon, navré, ce triste sire ne m'intéresse vraiment pas, bien au contraire il me désole et me consterne.

La seule vertu que je lui trouve, c'est qu'il me fournit l'occasion de démontrer que mes petits algorithmes peuvent transformer même le nom d'un type aussi peu enthousiasmant en problème intellectuel sympa. Décidément, l'algorithmique a des beautés que la politique n'atteindra jamais.

Petitagore a écrit: contrairement à lui, qui fait l'effet d'un inintéressant médiocre parce qu'il l'est bel et bien.

Je peux comprendre qu'on ne l'aime pas, lui, sa France, son parti, et tout le reste autour. Mais dire que tout ça est moyen, inintéressant et ultra simple; c'est se défouler gratuitement. Un peu absurde quoi.

Stauk a écrit:Je peux comprendre qu'on ne l'aime pas, lui, sa France, son parti, et tout le reste autour. Mais dire que tout ça est moyen, inintéressant et ultra simple; c'est se défouler gratuitement.

Ah bon, tu l'avais remarqué?

Je ne suis pas sûr d'avoir le temps de vous donner des réponses complètes aujourd'hui, mais voici déjà, à mon sens, les trois meilleurs cavexes pour résoudre la grille "sarkozy":



Simples, élégants et de bon goût...

Mais sur cette même grille "sarkozy", on pouvait aussi employer quelques autres cavexes sensiblement moins élégants:



Vous avez donc l'embarras du choix. Par tempérament, je préfère les cavexes concis, mais les solutions sont parfois plus simples à trouver quand il n'y a plus que quelques cases pour jouer les premiers coups.

Bonjour bonjour... Voici les solutions de la grille "sarkozy" correspondant aux cavexes publiés hier. Bon, pour le principe, je vous les mets sous spoiler:

Solutions complètes:

Je ne pense pas publier de nouveau problème aujourd'hui. Profitez-en pour réviser!

Le problème du jour sera la grille "hollande", grâce à laquelle nous achèverons la série des présidents de la République, et c'est pas dommage:



Vu le mal que j'ai dit récemment de Sarkozy, il serait décent que je décoche aussi quelques piques au président en exercice pour rétablir l'équilibre... mais justement, j'ai un peu peur que ce ne soit pas équilibré, tellement l'évocation de ce bon gros joufflu jovial a tendance à me mettre en fureur et à me faire péter les plombs. Comment y aller mollo?

Peut-être en me limitant à celle de ses trahisons pour laquelle je n'ai pas réussi, pas même une demi-seconde à titre purement rhétorique, à essayer de relativiser, à me dire qu'il croyait peut-être sincèrement à ce qu'il faisait, qu'il n'était pas forcément vendu mais peut-être tout simplement bête... J'ai été effaré, choqué (shocking!), révolté, hystérisé, quand la France de Hollande a interdit de survol de son territoire l'avion du président bolivien Morales sous le prétexte d'ailleurs totalement faux qu'Edward Snowden pouvait se trouver à son bord. Dieu sait si je n'avais pas une haute estime de Hollande jusque là, mais cette démonstration de servilité intégrale m'a coupé les pattes par son absolue bassesse. Tout ce qu'on demandait à ce gros connard en l'occurrence, c'était d'être conforme à son tempérament, de temporiser, de faire celui qui n'a pas compris ce que l'Otan demandait, et trop pris le temps de réfléchir (Dieu sait qu'il est capable d'en jouer!), de façon qu'il puisse tout de suite dire oups, trop tard, l'avion est déjà passé, bon ben s'il n'y a plus de solution il n'y a plus de problème.

Evidemment, ce qu'il aurait vraiment fallu faire, ç'aurait été d'offrir l'asile politique à Snowden, de l'accueillir en personne à sa descente d'avion avec le tapis rouge pour le faire immédiatement Grand-Croix de la Légion d'Honneur, mais pour ça il aurait fallu du panache, chose dont notre bon gros président est intégralement dépourvu... Tant pis, en l'occurrence, il lui aurait suffi d'être raisonnablement minable comme à son habitude, en conformité totale avec son tempérament. Ça ne présentait aucune difficulté, ça n'aurait entraîné aucune répercussion diplomatique... et tout au contraire ce sale larbin a absolument tenu à déshonorer mon pays et provoquer un incident diplomatique par un acte de guerre (parce que bloquer le passage pacifique d'un chef d'Etat étranger, c'est un acte de guerre), pour rien, sans même réussir à bloquer Snowden (ce qui aurait été ignominieusement scandaleux mais aurait au moins évité le ridicule)... Après quoi il n'a même pas cherché à faire semblant de s'excuser. Minable, minable, minable.

Ajoutez à ça que j'ai vécu quatre ans en Bolivie, que je connais un peu la mentalité pacifiquement francophile des adorateurs de la Pachamama, et que je vous assure que pour se fâcher avec des gens si tranquilles il faut vraiment en faire des tonnes.

Bref, Hollande, berk. Pauvre type, minable. Larbin. On voit bien qu'il a été élu parce qu'il était le plus bête, selon la formule de Clemenceau, mais en l'occurrence il n'a pas fait preuve de bêtise, mais d'ignominie dans la servilité. C'est aussi bas que d'avoir laissé camper le harem de Kadhafi dans les jardins de l'Elysée (allez, parlons un peu de Sarko pour rétablir l'équilibre), mais en plus, c'est minable.

Ahem. Je me calme.

A part ça, la grille "hollande" comporte au moins un cavexe très très simple, qui peut vous permettre d'y atteindre l'optimum en deux coups de cuiller à pot, vraiment comme à l'exercice, c'est du gâteau, lâchez-vous.

Eh bien, en fait, la solution qui m'a sauté aux yeux est... pratiquement la seule: la grille "hollande" ne peut guère être résolue qu'avec l'un de ces deux cavexes, qui sont clairement deux variantes de la même idée:



Il y en a encore parmi vous à qui on a besoin d'expliquer pourquoi il faut chercher à terminer la résolution de cette grille sur un hexagone marié à un pentagone? C'est en relation directe avec le nombre de cases, 38 en l'occurrence, c'est-à-dire 2 (deux cases bleues sacrifiées au début) + 36 -- qui est un multiple de trois, donc il faut terminer sur un polygone convexe dont le nombre de cases est lui-même un multiple de trois (un hexagone, quoi)... J'ai déjà expliqué ça cent millions de fois, par exemple ici. Par ailleurs, l'avant-dernier coup doit être joué à proximité de ce polygone convexe final (qui dans le cas qui nous occupe est donc un hexagone), mais pas n'importe où non plus, sur un pentagone, en vertu du théorème de l'avant-dernier coup expliqué ici et que tout joueur de Triancey doit connaître par coeur de la même façon qu'un premier communiant doit savoir le Credo.

Les deux hexagones employés par les cavexes ci-dessus ne sont pas tout à fait les seuls de la grille "hollande" qui soient mariés à des pentagones (cela dit, cette grille est inhabituellement pauvre en pentagones)... mais mon solveur a l'air de dire que ce sont les seuls utilisables.

Quoi qu'il en soit, une fois qu'on a identifié l'un quelconque de ces deux cavexes, la résolution de la grille, c'est vraiment de la gnognotte, du gâteau, piece of cake comme on dit outre-Manche. Suggestion: prenez une colonne, puis une autre, puis une troisième, puis le cavexe. Poum, poum, poum, schlak, c'est vraiment efficace, carré, prussien, "black et d'équerre" comme disait un collègue à moi... c'est inratable.

Solutions complètes ce soir -- mais j'ose espérer que vous aurez trouvé tous seuls bien avant.

Allez, exécutons cette grille "hollande" proprement et sans bavures. C'est tellement facile que je ne vous le mets même pas sous spoiler.

Avec le cavexe 0. Allons-y pour la première colonne: 4, 21 (bleus), 11, 34 (jaunes); et voilà une colonne de faite. Allons-y pour la deuxième colonne: 12, 37, 22 (des questions?). Allons-y pour la troisième colonne: 14, 0, 23. Allons-y pour le cavexe: 15, 24 (jaune), et n'importe quoi pour terminer (sur un hexagone bleu). Vous voyez, je ne vous avais pas menti: c'est vraiment poum, poum, poum, schlak.

Avec le cavexe 1. Bah, c'est le même topo ou presque. Allons-y pour la première colonne: 2, 20 (cases isolées bleues), 8, 30 (jaunes), et voilà  une première colonne de faite. Allons-y pour la deuxième colonne: 23, 0, 14. Allons-y pour la troisième colonne: 17, 6, 27. Allons-y pour le cavexe: 16, 25, et un dernier coup indifférent pour prendre en bleu l'hexagone final. Poum, poum, poum, schlak.

Ah, si la vie pouvait toujours être aussi facile...

Bon, eh bien, aujourd'hui, par contraste, nous allons nous attaquer à une grille difficile, mais alors, une difficile de chez Difficile Père et Fils. Le problème du jour sera la grille "fevrier".



J'ai envie de ne rien vous dire du tout et de vous laisser vous dépatouiller. Parce que moi, contrairement à vous bande de feignasses, je ne me décourage pas facilement, et quand finalement je demande la solution à mon solveur, c'est vraiment parce que j'ai tout essayé, mais alors tout, ce qui s'appelle tout. Sauf, bien sûr, la solution qui marche... et qui n'était même pas cachée, en fait (rien n'est jamais caché sur une grille Triancey, c'est un problème NP-complet comme disent les matheux et du diable si je sais ce qu'ils entendent par là à part "si tu ne trouves pas, c'est de ta faute, connard!"). Eeeh non, la solution n'est pas cachée. Elle n'est pas super-visible non plus, mais par rapport aux tonnes de solutions tordues que j'ai essayées, elle est quand même relativement simple. Et c'est vexaaaaant!

Allez, zut, démerdez-vous. Je vous donnerai des indices plus tard, quand j'aurai le sentiment que vous avez un peu cherché.

Bon, allez, je vous aide un peu.

J'ose espérer que les plus assidus d'entre vous ont compris seuls que nous avions affaire à une grille "cinq ou huit": quarante cases moins deux sacrifiées au départ pour initier la série de coups gagnants, reste 38 qui est un multiple de trois majoré de deux. Ergo, dans l'idéal il faudrait jouer le dernier coup sur un polygone convexe dont le nombre de cases soit lui-même un multiple de trois majoré de deux, c'est-à-dire un pentagone. Et (tous en choeur), en vertu du théorème de l'avant-dernier coup, nous savons que ce pentagone final devra lui-même être marié à un autre pentagone, et donc nous sommes à la recherche d'un couple de pentagones pour terminer la résolution de la grille.

Cette grille n'est pas dépourvue de tout couple de pentagones, et les cases 28, 29, 30, 35 à 39 en constituent un joli et même pas caché.

Seulement, terminer dessus n'a pas l'air simple, cornegidouille. Cette grille "fevrier" comporte aussi deux quadrilatères (2, 3, 9, 10 en haut, 26, 31, 32, 33 en bas à gauche), et je pense que vous avez déjà remarqué l'exaspérante tendance qu'ont les quadrilatères à toujours tout faire foirer.

Après un paquet d'essais infructueux pour terminer sur le couple de pentagones sus-cité, peut-être vous êtes-vous fait la même réflexion que moi, réflexion assez naturelle sur une grille "cinq ou huit": "Vu que ça n'a pas l'air possible de terminer sur le couple de pentagones, je vais déjà essayer de terminer en perdant huit cases au dernier coup, because non seulement ça me permettra de mieux comprendre la cohérence de la grille, mais si ça se trouve il n'y a pas de meilleure solution disponible." C'est en effet comme ça que je m'y prends d'ordinaire avec les grilles "cinq ou huit": je commence par viser le couple de pentagones, si ça n'a pas l'air de marcher je termine sur huit cases (sur un couloir ou un octogone), et une fois que j'y suis parvenu, vu que ça m'a rasséréné, je réessaie le couple de pentagones à tout hasard avant de crier grâce et de demander à mon solveur si par hasard je ne serais pas en présence d'une grille insoluble (car il en existe bel et bien sur lesquelles il est complètement inutile de s'escrimer).

Mais allez donc terminer cette grille sur huit cases, vous m'en direz des nouvelles.

Ce n'est pas que les couloirs de huit cases en soient absents: 14, 18, 19, 15, 11, 16, 13, 17, ça nous en fait un; 25, 18, 19, 20, 21, 22, 23, 24, ça nous en fait deux; 4, 3, 10, 15, 19, 20, 27, 34, ça nous en fait trois. Et en général, terminer sur un couloir de huit cases, c'est de la gnognotte. Donc j'y vais la fleur au fusil... et je m'y casse les dents. Vingt fois, trente fois.

Et là, erreur fatale: je crie grâce. Quand c'est aussi difficile à terminer sur huit, il paraît évident que c'est inutile d'essayer de terminer sur cinq, vu que c'est dans l'immense majorité des cas beaucoup plus difficile.

Eh bien, honnêtement, je ne sais pas si on peut terminer sur huit. Mais on peut bel et bien terminer sur le couple de pentagones sus-cité. Et pas seulement avec des "cavexes à mortaise" inimaginables. On peut même y arriver avec de bons cavexes orthodoxes, dont un qui n'a vraiment rien de particulier, qui est au contraire de la plus complète orthodoxie, qui n'est même pas caché autour des quatre coins ou réparti sur deux bords: il est là, visible comme le nez au milieu de la figure... une fois qu'on le connaît.

Et voilà, je suis horriblement vexé. Saleté de grille "février"!

Bon, ben vous, contrairement à moi, vous n'avez plus l'excuse d'ignorer si le chat noir que vous cherchez à attraper se trouve ou non dans la pièce sombre: promis, juré, il y est.

Alors trouvez-le!

Vengez-moi!

Quand on n'arrive pas à dessiner des cavexes rondouillards et inversibles (il est rare que ce soit totalement impossible, mais ça arrive quand même; nous en avons vu un exemple avec la grille "septembre" dans celui de mes posts où je vous parlais des vignettes Panini, si vous vous souvenez), on peut encore en théorie faire quelques tentatives avec des cavexes "à mortaise". Personnellement, je trouve que c'est presque mission impossible, car on n'a a priori aucun indice pour soupçonner à quel endroit de la grille ça pourrait marcher: des ensembles tenon-mortaise, on peut en imaginer absolument partout (n'importe quelle case peut faire office de tenon, et celles qui entourent deux quelconques de ses côtés de mortaise), et il n'y aucune raison de penser que ça va mieux fonctionner ici que là.

Aucune aucune? Pas tout à fait... Il y a quand même des ensembles tenons-mortaises assez compréhensibles: ce sont ces foutus quadrilatères, ceux-là même qui donnent l'impression de toujours tout faire foirer: si on prend une case dans un quadrilatère, ça nous fait un tenon, et les trois autres qui sont autour dans le même quadrilatère font une belle mortaise qu'on peut espérer prendre ultérieurement en un seul coup gagnant. J'ai souvent constaté que cette astuce est employée (parmi d'autres, mais celle-là n'a pas trop l'air inimaginable et extraterrestre) par mon solveur pour trouver une solution à un "cinq ou huit" qui a tellement récalcitré face à moi que je commençais à me croire autorisé à le déclarer insoluble.

J'ai vaguement soupçonné qu'une solution de ce type devait pouvoir être trouvée sur la grille "fevrier", en dessinant un cavexe "à mortaise" horizontal dans le bas de la grille, englobant le couple de pentagones du coin inférieur droit et trois cases du quadrilatère en bas à gauche. Ce n'était pas bête et en effet mon solveur y parvient... sauf que pour le faire il exploite aussi une autre particularité de cette même grille qui m'avait échappée, obnubilé que j'étais par la recherche d'un cavexe horizontal bien coincé contre le bord inférieur (eh ben non: il vaut mieux qu'il déborde un peu...). Or, cette particularité est essentielle à la résolution de cette grille... au point que quand on l'a trouvée, elle permet de dessiner non seulement le cavexe à mortaise horizontal que je fantasmais, mais aussi un très beau cavexe rondouillard tout ce qu'il y a de plus orthodoxe.

Ha ha. Ce que je vous dis là, ça fait quand même plein plein d'indices. Saurez-vous en faire quelque chose?

Allez, je vous explique...:

Bon, allez, je continue de vous mettre sur la voie pour la résolution de la grille "fevrier" (j'espère que vous appréciez ma maîtrise consommée du teasing -- d'autant plus qu'elle est largement involontaire: je publie les éléments à mesure qu'ils sont prêts, c'est tout).

Voici le cavexe "à mortaise" horizontal que j'avais fantasmé mais pas réussi (comme toujours avec les cavexes "à mortaise", non inversibles par nature, je ne peux pas vous le montrer "en négatif", et donc sur le schéma qui suit les cases jaunes représentent par exception les premiers coups de la partie; le cavexe est donc constitué des cases noires restantes):



Vous l'avez, je l'espère, compris seuls: le "tenon", c'est la case 26, la "mortaise", ce sont les trois autres cases du quadrilatère: 31, 32, 33.

Bon. Mais maintenant que nous avons compris qu'il fallait inclure le troisième pentagone 4, 5, 34, 35, 36 dans le cavexe, y compris les deux petites cases 4 et 5 tout là-haut là-haut, n'y a-t-il pas un moyen de dessiner un bon cavexe rondouillard des familles? Si fait. Le voici:



Et vous voyez qu'il n'était absolument pas caché, ce salopard; certes, il est un peu massif, mais ça n'a rien d'inhabituel. J'aurais dû le voir, mais quelle andouille je fais, aargh, j'ai honte!

Bon, pour le même prix, je vous signale que mon solveur a trouvé un autre cavexe parfaitement orthodoxe, même s'il est sensiblement moins évident, avec ce quadrilatère qu'il a l'air de coincer sous son aisselle:



Et pour être tout à fait exhaustif, comme je sens que vous commencez à prendre goût aux cavexes "à mortaise", voici encore une variante de celui que nous avons déjà vu, avec la case 32 en guise de tenon mais à part ça c'est à peu près la même idée que tout au début de ce post (et évidemment, comme toujours avec les cavexes "à mortaise", le cavexe est ci-dessous représenté par les cases noires inoccupées):



Voilà voilà. Solutions complètes... un peu plus tard, mais je pense que vous avez déjà compris la différence entre une grille insoluble et une grille "seulement" très difficile.

N'hésitez pas à achever de m'humilier en me démontrant qu'en plus il était possible de terminer cette grille sur un couloir de huit, ce que j'ai vainement cherché à faire pendant plusieurs dizaines de minutes (cela dit, ce sera vraiment pour le plaisir de m'humilier, car en l'espèce il ne s'agira pas d'un optimum).

Allez, finissons-en avec cette grille "fevrier":

Solutions complètes:

Bon week-end... Pas sûr que j'alimente ce fil avant la semaine prochaine.

Bonjour, ça va? Le problème du jour sera la grille "juillet".



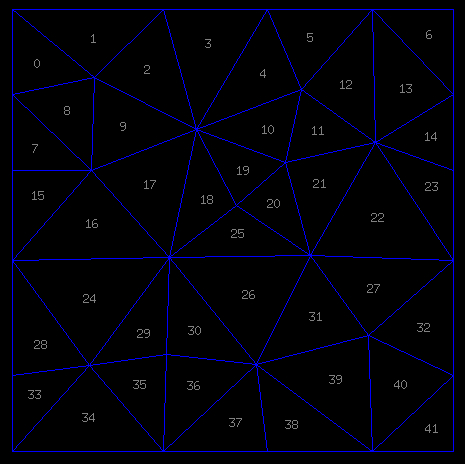
Je doute que vous vous en souveniez, mais dans l'inventaire commenté des grilles disponibles que j'ai publié il y a bientôt deux mois (mon Dieu, comme le temps passe), cette grille "juillet" était notée comme particulière. Aha. Et qu'est-ce qu'elle a-t-elle donc de particulier, la coquine?

Moi, ce que je remarque d'emblée sur une grille pareille (je ne sais pas l'effet que ça vous fait à vous), c'est qu'elle comporte en plein milieu une ligne horizontale presque parfaite (au-dessus des cases 24, 26, 27) alors qu'il est rarissime de rencontrer de tels alignements ailleurs que sur les bords. Eh bien, la particularité... ça n'est pas ça, car ça, c'est une particularité qui n'a aucune incidence sur la façon de résoudre la grille, donc en fait on s'en fout complètement, c'est un pur hasard sans signification et sans conséquence. Ce qu'il faut remarquer, c'est... autre chose.

Quoi donc?

Eh bien non, je ne vous le dirai pas. Il y a de cela fort longtemps, quand j'essayais de devenir un bon joueur d'échecs (je vous rassure, j'ai totalement échoué), je me suis tapé la lecture d'un bouquin d'un nommé Alexandre Koblentz (ça s'appelait "l'Entraînement aux échecs - la Route du succès"), qui était entraîneur de l'équipe soviétique d'échecs, excusez du peu. Vous êtes trop jeunots pour vous en souvenir, mais il n'y avait guère qu'un domaine sportif où les Soviétiques excellaient sans avoir recours au dopage, et c'était le jeu d'échecs, ils en étaient très fiers et le mettaient particulièrement en valeur ("Il n'y a pas beaucoup d'occasions de démontrer que le communisme a du bon", raillait le champion d'échecs et dissident soviétique Victor Kortchnoï). Ah, ouais, quand les Popov jouaient aux échecs, personne ne rigolait, un moujik derrière un échiquier, ça vous faisait penser la même chose que Bruce Lee quand il empoignait son nunchaku: "Putain, je suis foutu, j'ai aucune chance".

Eh bien, dans son bouquin, Koblentz publiait classiquement des tas de grilles d'échecs, mais il ne les accompagnait jamais des mentions traditionnelles "les blancs jouent et font mat en trois coups" ou "les blancs jouent et font nulle", et il affirmait que c'était à la base du succès des Popov: "Quand vous jouez aux échecs, vous n'avez pas à côté de vous un Père Noël qui vous indique ce qu'il faut faire." C'était très matérialiste dialectique et athée, mais ça me paraissait plein de sens. Ça ne m'a absolument pas aidé à cesser d'être le joueur d'échecs archi-nul que je suis toujours, mais j'ai quand même retenu la leçon et je ne vous dirai pas ce qu'il faut faire sur la grille du jour, na. Faudra que vous le trouviez tout seuls. Je ne vous donne qu'un indice: si vous ne remarquez rien de particulier sur cette grille, ben ça veut dire que vous n'y atteindrez pas l'optimum. Et l'air de rien, vous dire ça, c'est déjà vous aider beaucoup!