Petit jeujeu mathématique deviendra gros casse-tête

Il n'y a pas une foule de bons cavexes pour résoudre la grille "jeudi". Quand je fais plancher mon solveur, dessus, la plupart du temps il atteint l'optimum en employant des cavexes "à mortaise", non inversibles, du genre de celui-ci que je trouve assez ingénieux:



(N'oubliez pas que quand je cherche à vous décrire un cavexe "à mortaise", les cases jaunes représentent les premiers coups de la partie, au contraire de ce que je fais habituellement: d'ordinaire, sur l'image d'un cavexe, les cases colorées désignent la zone où il faudra jouer la fin de la partie et non pas son début. Je sais, tout cela est terriblement contre-intuitif... mais le caractère non inversible des cavexes "à mortaise" l'impose. Et puis, de toute façon, par nature un casse-tête n'est pas un truc intuitif, faudra vous y faire!)

Cela étant, il y a quand même quelques bons cavexes inversibles et rondouillards concevables, même s'ils ne brillent pas par la concision:



Il est peut-être possible d'en dessiner d'autres, mais ces quatre-là sont à l'heure où je vous parle les seuls dont je sois sûr qu'ils peuvent être employés pour atteindre l'optimum.

Solutions complètes dans la soirée, voire dans la nuit.

Avant de balancer les solutions complètes de la grille "jeudi", il faut que j'ajoute un dernier cavexe (appelons-le le cavexe 3) que mon solveur a imaginé entre-temps et qui est peut-être le meilleur du lot:



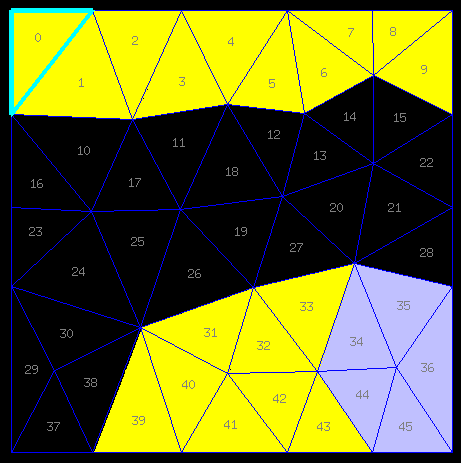
Et cette omission étant réparée...

... allons-y pour les solutions complètes:

Vous voyez que ç'aurait été bougrement dommage de déclarer cette grille insoluble, même si elle n'était pas vraiment simple.

Le problème du jour sera la grille "mitterrand".



Pour les gens de ma génération (j'avais vingt ans quand Mitterrand a été élu, et à ma courte honte je dois dire que j'ai voté pour lui, fait la fête à la Bastille et tout le toutim), il est tentant de faire une comparaison avec cette grille et la grille "giscard" que nous avons vue il y a peu. Les deux grilles ont d'ailleurs le même nombre de cases, donc les raisonnements arithmétiques qu'elles appellent toutes deux sont totalement similaires au départ.

Rappelons-les, la répétition étant la base même de la pédagogie...

Pour entamer la série ininterrompue de coups gagnants (jaunes) qui constitue l'objectif de ce jeu, il faut sauf exceptions rarissimes commencer par sacrifier deux cases isolées (bleues) sur toute grille à laquelle on s'attaque. Quarante cases moins deux sacrifiées au départ, reste trente-huit. Trente-huit n'est pas un multiple de trois, mais un multiple de trois majoré de deux (ou minoré de un, ça revient au même), donc le dernier coup joué sur ces trente-huit cases restantes ne pourra pas être un coup gagnant, il faudra qu'il prenne un nombre de cases qui soit lui-même un multiple de trois majoré de deux. La plus petite quantité envisageable répondant à cette condition étant de cinq cases, nous savons que nous devons chercher sur cette grille un pentagone sur lequel jouer le dernier coup.

Seulement, avant le dernier coup, il y a l'avant-dernier, et le très important théorème de l'avant-dernier coup a établi qu'on ne peut atteindre un score optimal "classique" que si l'avant-dernier coup est lui-même joué sur un pentagone situé à proximité immédiate du polygone final... Donc nous cherchons sur la grille "mitterrand" dont je viens de publier l'image la même configuration que sur la grille "giscard" que nous avons étudiée naguère: nous cherchons un couple de pentagones, c'est-à-dire deux pentagones "mariés", possédant deux cases en commun.

Eh bien, ne vous cassez pas la nénette: sur la grille "giscard", ça existait, mais dans la maison "mitterrand", il n'y a rien de tel (à l'époque le Parti socialiste n'était pas encore infesté de tarlouzes mais je raye tout de suite cette vanne idiote car l'humour homophobe n'est pas ma tasse de thé). Donc, ce n'est pas la peine de fantasmer sur le score optimal "classique" (deux cases bleues sacrifiées au départ, un pentagone à l'avant-dernier coup et le plus petit polygone convexe possible au dernier coup), on n'est pas dans la catégorie maudite des grilles "cinq ou huit" et il faut tout simplement prendre non pas cinq, mais bien 5 + 3 = huit cases au dernier coup. La grille "giscard" vous donnait de faux espoirs (de terminer sur un pentagone), la grille "mitterrand" douche carrément votre enthousiasme d'emblée (je ne suis pas sûr qu'historiquement ça se soit vraiment passé comme ça lors de l'élection de ces deux tristes sires, mais en ce qui concerne mes grilles, je vous assure que je ne vous dis pas de sottises).

Bon, ben voilà. Terminer sur huit cases, d'ordinaire, est assez facile, donc allez-y gaiement. Mais méfiez-vous quand même: Mitterrand était un roublard, et ceux qui pensaient se défaire de lui en six mois ont quand même dû se le coltiner pendant deux septennats... Pareillement, cette grille est peut-être moins simple qu'il n'y paraît.

Allez, quelques pistes pour résoudre la grille "mitterrand":



J'ai honte, mais je n'ai pas vu les deux couloirs parfaitement utilisables que mon solveur, lui, n'a bien sûr pas ratés; apparemment, je n'arrive pas toujours à compter jusqu'à huit. En revanche, j'ai trouvé sans tricher le premier cavexe (et la solution qui va avec). Si vous n'avez rien fait de tout ça, eh bien je ne vous félicite pas.

Solutions complètes avant demain si je n'oublie pas.

Voici donc les solutions complètes pour la grille "mitterrand".

Solutions complètes:

Et bonne nuit à tous.

Il fallait bien que ça arrive un jour (quelle idée idiote j'ai eue de donner des noms de présidents de la République à mes grilles), le problème du jour sera la grille "sarkozy".



Le personnage ne m'inspire vraiment pas grand-chose d'autre que "casse-toi pôv'con", comme il le dit lui-même avec ce style distingué, raffiné, spirituel, cultivé et intellectuel que nous lui connaissons tous et qui convient si bien à un successeur des rois de France.

Je m'empresse de dire que la grille est plus intéressante que le personnage: elle est plus complexe qu'elle ne paraît -- contrairement à lui, qui fait l'effet d'un inintéressant médiocre parce qu'il l'est bel et bien.

Si ces propos peu aimables (et absolument pas argumentés; j'assume, ça n'en vaut pas la peine) m'aliènent des lecteurs... ben je m'en consolerai. Je n'irai pas jusqu'à leur dire "cassez-vous pôv'cons", parce que je suis un peu plus raffiné que le personnage et que je suppose (philanthropiquement) que leur âme peut être plus complexe que leur bulletin de vote... mais bon, navré, ce triste sire ne m'intéresse vraiment pas, bien au contraire il me désole et me consterne.

La seule vertu que je lui trouve, c'est qu'il me fournit l'occasion de démontrer que mes petits algorithmes peuvent transformer même le nom d'un type aussi peu enthousiasmant en problème intellectuel sympa. Décidément, l'algorithmique a des beautés que la politique n'atteindra jamais.

Petitagore a écrit: contrairement à lui, qui fait l'effet d'un inintéressant médiocre parce qu'il l'est bel et bien.

Je peux comprendre qu'on ne l'aime pas, lui, sa France, son parti, et tout le reste autour. Mais dire que tout ça est moyen, inintéressant et ultra simple; c'est se défouler gratuitement. Un peu absurde quoi.

Stauk a écrit:Je peux comprendre qu'on ne l'aime pas, lui, sa France, son parti, et tout le reste autour. Mais dire que tout ça est moyen, inintéressant et ultra simple; c'est se défouler gratuitement.

Ah bon, tu l'avais remarqué?

Je ne suis pas sûr d'avoir le temps de vous donner des réponses complètes aujourd'hui, mais voici déjà, à mon sens, les trois meilleurs cavexes pour résoudre la grille "sarkozy":



Simples, élégants et de bon goût...

Mais sur cette même grille "sarkozy", on pouvait aussi employer quelques autres cavexes sensiblement moins élégants:



Vous avez donc l'embarras du choix. Par tempérament, je préfère les cavexes concis, mais les solutions sont parfois plus simples à trouver quand il n'y a plus que quelques cases pour jouer les premiers coups.

Bonjour bonjour... Voici les solutions de la grille "sarkozy" correspondant aux cavexes publiés hier. Bon, pour le principe, je vous les mets sous spoiler:

Solutions complètes:

Je ne pense pas publier de nouveau problème aujourd'hui. Profitez-en pour réviser!

Le problème du jour sera la grille "hollande", grâce à laquelle nous achèverons la série des présidents de la République, et c'est pas dommage:



Vu le mal que j'ai dit récemment de Sarkozy, il serait décent que je décoche aussi quelques piques au président en exercice pour rétablir l'équilibre... mais justement, j'ai un peu peur que ce ne soit pas équilibré, tellement l'évocation de ce bon gros joufflu jovial a tendance à me mettre en fureur et à me faire péter les plombs. Comment y aller mollo?

Peut-être en me limitant à celle de ses trahisons pour laquelle je n'ai pas réussi, pas même une demi-seconde à titre purement rhétorique, à essayer de relativiser, à me dire qu'il croyait peut-être sincèrement à ce qu'il faisait, qu'il n'était pas forcément vendu mais peut-être tout simplement bête... J'ai été effaré, choqué (shocking!), révolté, hystérisé, quand la France de Hollande a interdit de survol de son territoire l'avion du président bolivien Morales sous le prétexte d'ailleurs totalement faux qu'Edward Snowden pouvait se trouver à son bord. Dieu sait si je n'avais pas une haute estime de Hollande jusque là, mais cette démonstration de servilité intégrale m'a coupé les pattes par son absolue bassesse. Tout ce qu'on demandait à ce gros connard en l'occurrence, c'était d'être conforme à son tempérament, de temporiser, de faire celui qui n'a pas compris ce que l'Otan demandait, et trop pris le temps de réfléchir (Dieu sait qu'il est capable d'en jouer!), de façon qu'il puisse tout de suite dire oups, trop tard, l'avion est déjà passé, bon ben s'il n'y a plus de solution il n'y a plus de problème.

Evidemment, ce qu'il aurait vraiment fallu faire, ç'aurait été d'offrir l'asile politique à Snowden, de l'accueillir en personne à sa descente d'avion avec le tapis rouge pour le faire immédiatement Grand-Croix de la Légion d'Honneur, mais pour ça il aurait fallu du panache, chose dont notre bon gros président est intégralement dépourvu... Tant pis, en l'occurrence, il lui aurait suffi d'être raisonnablement minable comme à son habitude, en conformité totale avec son tempérament. Ça ne présentait aucune difficulté, ça n'aurait entraîné aucune répercussion diplomatique... et tout au contraire ce sale larbin a absolument tenu à déshonorer mon pays et provoquer un incident diplomatique par un acte de guerre (parce que bloquer le passage pacifique d'un chef d'Etat étranger, c'est un acte de guerre), pour rien, sans même réussir à bloquer Snowden (ce qui aurait été ignominieusement scandaleux mais aurait au moins évité le ridicule)... Après quoi il n'a même pas cherché à faire semblant de s'excuser. Minable, minable, minable.

Ajoutez à ça que j'ai vécu quatre ans en Bolivie, que je connais un peu la mentalité pacifiquement francophile des adorateurs de la Pachamama, et que je vous assure que pour se fâcher avec des gens si tranquilles il faut vraiment en faire des tonnes.

Bref, Hollande, berk. Pauvre type, minable. Larbin. On voit bien qu'il a été élu parce qu'il était le plus bête, selon la formule de Clemenceau, mais en l'occurrence il n'a pas fait preuve de bêtise, mais d'ignominie dans la servilité. C'est aussi bas que d'avoir laissé camper le harem de Kadhafi dans les jardins de l'Elysée (allez, parlons un peu de Sarko pour rétablir l'équilibre), mais en plus, c'est minable.

Ahem. Je me calme.

A part ça, la grille "hollande" comporte au moins un cavexe très très simple, qui peut vous permettre d'y atteindre l'optimum en deux coups de cuiller à pot, vraiment comme à l'exercice, c'est du gâteau, lâchez-vous.

Eh bien, en fait, la solution qui m'a sauté aux yeux est... pratiquement la seule: la grille "hollande" ne peut guère être résolue qu'avec l'un de ces deux cavexes, qui sont clairement deux variantes de la même idée:



Il y en a encore parmi vous à qui on a besoin d'expliquer pourquoi il faut chercher à terminer la résolution de cette grille sur un hexagone marié à un pentagone? C'est en relation directe avec le nombre de cases, 38 en l'occurrence, c'est-à-dire 2 (deux cases bleues sacrifiées au début) + 36 -- qui est un multiple de trois, donc il faut terminer sur un polygone convexe dont le nombre de cases est lui-même un multiple de trois (un hexagone, quoi)... J'ai déjà expliqué ça cent millions de fois, par exemple ici. Par ailleurs, l'avant-dernier coup doit être joué à proximité de ce polygone convexe final (qui dans le cas qui nous occupe est donc un hexagone), mais pas n'importe où non plus, sur un pentagone, en vertu du théorème de l'avant-dernier coup expliqué ici et que tout joueur de Triancey doit connaître par coeur de la même façon qu'un premier communiant doit savoir le Credo.

Les deux hexagones employés par les cavexes ci-dessus ne sont pas tout à fait les seuls de la grille "hollande" qui soient mariés à des pentagones (cela dit, cette grille est inhabituellement pauvre en pentagones)... mais mon solveur a l'air de dire que ce sont les seuls utilisables.

Quoi qu'il en soit, une fois qu'on a identifié l'un quelconque de ces deux cavexes, la résolution de la grille, c'est vraiment de la gnognotte, du gâteau, piece of cake comme on dit outre-Manche. Suggestion: prenez une colonne, puis une autre, puis une troisième, puis le cavexe. Poum, poum, poum, schlak, c'est vraiment efficace, carré, prussien, "black et d'équerre" comme disait un collègue à moi... c'est inratable.

Solutions complètes ce soir -- mais j'ose espérer que vous aurez trouvé tous seuls bien avant.

Allez, exécutons cette grille "hollande" proprement et sans bavures. C'est tellement facile que je ne vous le mets même pas sous spoiler.

Avec le cavexe 0. Allons-y pour la première colonne: 4, 21 (bleus), 11, 34 (jaunes); et voilà une colonne de faite. Allons-y pour la deuxième colonne: 12, 37, 22 (des questions?). Allons-y pour la troisième colonne: 14, 0, 23. Allons-y pour le cavexe: 15, 24 (jaune), et n'importe quoi pour terminer (sur un hexagone bleu). Vous voyez, je ne vous avais pas menti: c'est vraiment poum, poum, poum, schlak.

Avec le cavexe 1. Bah, c'est le même topo ou presque. Allons-y pour la première colonne: 2, 20 (cases isolées bleues), 8, 30 (jaunes), et voilà  une première colonne de faite. Allons-y pour la deuxième colonne: 23, 0, 14. Allons-y pour la troisième colonne: 17, 6, 27. Allons-y pour le cavexe: 16, 25, et un dernier coup indifférent pour prendre en bleu l'hexagone final. Poum, poum, poum, schlak.

Ah, si la vie pouvait toujours être aussi facile...

Bon, eh bien, aujourd'hui, par contraste, nous allons nous attaquer à une grille difficile, mais alors, une difficile de chez Difficile Père et Fils. Le problème du jour sera la grille "fevrier".



J'ai envie de ne rien vous dire du tout et de vous laisser vous dépatouiller. Parce que moi, contrairement à vous bande de feignasses, je ne me décourage pas facilement, et quand finalement je demande la solution à mon solveur, c'est vraiment parce que j'ai tout essayé, mais alors tout, ce qui s'appelle tout. Sauf, bien sûr, la solution qui marche... et qui n'était même pas cachée, en fait (rien n'est jamais caché sur une grille Triancey, c'est un problème NP-complet comme disent les matheux et du diable si je sais ce qu'ils entendent par là à part "si tu ne trouves pas, c'est de ta faute, connard!"). Eeeh non, la solution n'est pas cachée. Elle n'est pas super-visible non plus, mais par rapport aux tonnes de solutions tordues que j'ai essayées, elle est quand même relativement simple. Et c'est vexaaaaant!

Allez, zut, démerdez-vous. Je vous donnerai des indices plus tard, quand j'aurai le sentiment que vous avez un peu cherché.

Bon, allez, je vous aide un peu.

J'ose espérer que les plus assidus d'entre vous ont compris seuls que nous avions affaire à une grille "cinq ou huit": quarante cases moins deux sacrifiées au départ pour initier la série de coups gagnants, reste 38 qui est un multiple de trois majoré de deux. Ergo, dans l'idéal il faudrait jouer le dernier coup sur un polygone convexe dont le nombre de cases soit lui-même un multiple de trois majoré de deux, c'est-à-dire un pentagone. Et (tous en choeur), en vertu du théorème de l'avant-dernier coup, nous savons que ce pentagone final devra lui-même être marié à un autre pentagone, et donc nous sommes à la recherche d'un couple de pentagones pour terminer la résolution de la grille.

Cette grille n'est pas dépourvue de tout couple de pentagones, et les cases 28, 29, 30, 35 à 39 en constituent un joli et même pas caché.

Seulement, terminer dessus n'a pas l'air simple, cornegidouille. Cette grille "fevrier" comporte aussi deux quadrilatères (2, 3, 9, 10 en haut, 26, 31, 32, 33 en bas à gauche), et je pense que vous avez déjà remarqué l'exaspérante tendance qu'ont les quadrilatères à toujours tout faire foirer.

Après un paquet d'essais infructueux pour terminer sur le couple de pentagones sus-cité, peut-être vous êtes-vous fait la même réflexion que moi, réflexion assez naturelle sur une grille "cinq ou huit": "Vu que ça n'a pas l'air possible de terminer sur le couple de pentagones, je vais déjà essayer de terminer en perdant huit cases au dernier coup, because non seulement ça me permettra de mieux comprendre la cohérence de la grille, mais si ça se trouve il n'y a pas de meilleure solution disponible." C'est en effet comme ça que je m'y prends d'ordinaire avec les grilles "cinq ou huit": je commence par viser le couple de pentagones, si ça n'a pas l'air de marcher je termine sur huit cases (sur un couloir ou un octogone), et une fois que j'y suis parvenu, vu que ça m'a rasséréné, je réessaie le couple de pentagones à tout hasard avant de crier grâce et de demander à mon solveur si par hasard je ne serais pas en présence d'une grille insoluble (car il en existe bel et bien sur lesquelles il est complètement inutile de s'escrimer).

Mais allez donc terminer cette grille sur huit cases, vous m'en direz des nouvelles.

Ce n'est pas que les couloirs de huit cases en soient absents: 14, 18, 19, 15, 11, 16, 13, 17, ça nous en fait un; 25, 18, 19, 20, 21, 22, 23, 24, ça nous en fait deux; 4, 3, 10, 15, 19, 20, 27, 34, ça nous en fait trois. Et en général, terminer sur un couloir de huit cases, c'est de la gnognotte. Donc j'y vais la fleur au fusil... et je m'y casse les dents. Vingt fois, trente fois.

Et là, erreur fatale: je crie grâce. Quand c'est aussi difficile à terminer sur huit, il paraît évident que c'est inutile d'essayer de terminer sur cinq, vu que c'est dans l'immense majorité des cas beaucoup plus difficile.

Eh bien, honnêtement, je ne sais pas si on peut terminer sur huit. Mais on peut bel et bien terminer sur le couple de pentagones sus-cité. Et pas seulement avec des "cavexes à mortaise" inimaginables. On peut même y arriver avec de bons cavexes orthodoxes, dont un qui n'a vraiment rien de particulier, qui est au contraire de la plus complète orthodoxie, qui n'est même pas caché autour des quatre coins ou réparti sur deux bords: il est là, visible comme le nez au milieu de la figure... une fois qu'on le connaît.

Et voilà, je suis horriblement vexé. Saleté de grille "février"!

Bon, ben vous, contrairement à moi, vous n'avez plus l'excuse d'ignorer si le chat noir que vous cherchez à attraper se trouve ou non dans la pièce sombre: promis, juré, il y est.

Alors trouvez-le!

Vengez-moi!

Quand on n'arrive pas à dessiner des cavexes rondouillards et inversibles (il est rare que ce soit totalement impossible, mais ça arrive quand même; nous en avons vu un exemple avec la grille "septembre" dans celui de mes posts où je vous parlais des vignettes Panini, si vous vous souvenez), on peut encore en théorie faire quelques tentatives avec des cavexes "à mortaise". Personnellement, je trouve que c'est presque mission impossible, car on n'a a priori aucun indice pour soupçonner à quel endroit de la grille ça pourrait marcher: des ensembles tenon-mortaise, on peut en imaginer absolument partout (n'importe quelle case peut faire office de tenon, et celles qui entourent deux quelconques de ses côtés de mortaise), et il n'y aucune raison de penser que ça va mieux fonctionner ici que là.

Aucune aucune? Pas tout à fait... Il y a quand même des ensembles tenons-mortaises assez compréhensibles: ce sont ces foutus quadrilatères, ceux-là même qui donnent l'impression de toujours tout faire foirer: si on prend une case dans un quadrilatère, ça nous fait un tenon, et les trois autres qui sont autour dans le même quadrilatère font une belle mortaise qu'on peut espérer prendre ultérieurement en un seul coup gagnant. J'ai souvent constaté que cette astuce est employée (parmi d'autres, mais celle-là n'a pas trop l'air inimaginable et extraterrestre) par mon solveur pour trouver une solution à un "cinq ou huit" qui a tellement récalcitré face à moi que je commençais à me croire autorisé à le déclarer insoluble.

J'ai vaguement soupçonné qu'une solution de ce type devait pouvoir être trouvée sur la grille "fevrier", en dessinant un cavexe "à mortaise" horizontal dans le bas de la grille, englobant le couple de pentagones du coin inférieur droit et trois cases du quadrilatère en bas à gauche. Ce n'était pas bête et en effet mon solveur y parvient... sauf que pour le faire il exploite aussi une autre particularité de cette même grille qui m'avait échappée, obnubilé que j'étais par la recherche d'un cavexe horizontal bien coincé contre le bord inférieur (eh ben non: il vaut mieux qu'il déborde un peu...). Or, cette particularité est essentielle à la résolution de cette grille... au point que quand on l'a trouvée, elle permet de dessiner non seulement le cavexe à mortaise horizontal que je fantasmais, mais aussi un très beau cavexe rondouillard tout ce qu'il y a de plus orthodoxe.

Ha ha. Ce que je vous dis là, ça fait quand même plein plein d'indices. Saurez-vous en faire quelque chose?

Allez, je vous explique...:

Bon, allez, je continue de vous mettre sur la voie pour la résolution de la grille "fevrier" (j'espère que vous appréciez ma maîtrise consommée du teasing -- d'autant plus qu'elle est largement involontaire: je publie les éléments à mesure qu'ils sont prêts, c'est tout).

Voici le cavexe "à mortaise" horizontal que j'avais fantasmé mais pas réussi (comme toujours avec les cavexes "à mortaise", non inversibles par nature, je ne peux pas vous le montrer "en négatif", et donc sur le schéma qui suit les cases jaunes représentent par exception les premiers coups de la partie; le cavexe est donc constitué des cases noires restantes):



Vous l'avez, je l'espère, compris seuls: le "tenon", c'est la case 26, la "mortaise", ce sont les trois autres cases du quadrilatère: 31, 32, 33.

Bon. Mais maintenant que nous avons compris qu'il fallait inclure le troisième pentagone 4, 5, 34, 35, 36 dans le cavexe, y compris les deux petites cases 4 et 5 tout là-haut là-haut, n'y a-t-il pas un moyen de dessiner un bon cavexe rondouillard des familles? Si fait. Le voici:



Et vous voyez qu'il n'était absolument pas caché, ce salopard; certes, il est un peu massif, mais ça n'a rien d'inhabituel. J'aurais dû le voir, mais quelle andouille je fais, aargh, j'ai honte!

Bon, pour le même prix, je vous signale que mon solveur a trouvé un autre cavexe parfaitement orthodoxe, même s'il est sensiblement moins évident, avec ce quadrilatère qu'il a l'air de coincer sous son aisselle:



Et pour être tout à fait exhaustif, comme je sens que vous commencez à prendre goût aux cavexes "à mortaise", voici encore une variante de celui que nous avons déjà vu, avec la case 32 en guise de tenon mais à part ça c'est à peu près la même idée que tout au début de ce post (et évidemment, comme toujours avec les cavexes "à mortaise", le cavexe est ci-dessous représenté par les cases noires inoccupées):



Voilà voilà. Solutions complètes... un peu plus tard, mais je pense que vous avez déjà compris la différence entre une grille insoluble et une grille "seulement" très difficile.

N'hésitez pas à achever de m'humilier en me démontrant qu'en plus il était possible de terminer cette grille sur un couloir de huit, ce que j'ai vainement cherché à faire pendant plusieurs dizaines de minutes (cela dit, ce sera vraiment pour le plaisir de m'humilier, car en l'espèce il ne s'agira pas d'un optimum).

Allez, finissons-en avec cette grille "fevrier":

Solutions complètes:

Bon week-end... Pas sûr que j'alimente ce fil avant la semaine prochaine.

Bonjour, ça va? Le problème du jour sera la grille "juillet".



Je doute que vous vous en souveniez, mais dans l'inventaire commenté des grilles disponibles que j'ai publié il y a bientôt deux mois (mon Dieu, comme le temps passe), cette grille "juillet" était notée comme particulière. Aha. Et qu'est-ce qu'elle a-t-elle donc de particulier, la coquine?

Moi, ce que je remarque d'emblée sur une grille pareille (je ne sais pas l'effet que ça vous fait à vous), c'est qu'elle comporte en plein milieu une ligne horizontale presque parfaite (au-dessus des cases 24, 26, 27) alors qu'il est rarissime de rencontrer de tels alignements ailleurs que sur les bords. Eh bien, la particularité... ça n'est pas ça, car ça, c'est une particularité qui n'a aucune incidence sur la façon de résoudre la grille, donc en fait on s'en fout complètement, c'est un pur hasard sans signification et sans conséquence. Ce qu'il faut remarquer, c'est... autre chose.

Quoi donc?

Eh bien non, je ne vous le dirai pas. Il y a de cela fort longtemps, quand j'essayais de devenir un bon joueur d'échecs (je vous rassure, j'ai totalement échoué), je me suis tapé la lecture d'un bouquin d'un nommé Alexandre Koblentz (ça s'appelait "l'Entraînement aux échecs - la Route du succès"), qui était entraîneur de l'équipe soviétique d'échecs, excusez du peu. Vous êtes trop jeunots pour vous en souvenir, mais il n'y avait guère qu'un domaine sportif où les Soviétiques excellaient sans avoir recours au dopage, et c'était le jeu d'échecs, ils en étaient très fiers et le mettaient particulièrement en valeur ("Il n'y a pas beaucoup d'occasions de démontrer que le communisme a du bon", raillait le champion d'échecs et dissident soviétique Victor Kortchnoï). Ah, ouais, quand les Popov jouaient aux échecs, personne ne rigolait, un moujik derrière un échiquier, ça vous faisait penser la même chose que Bruce Lee quand il empoignait son nunchaku: "Putain, je suis foutu, j'ai aucune chance".

Eh bien, dans son bouquin, Koblentz publiait classiquement des tas de grilles d'échecs, mais il ne les accompagnait jamais des mentions traditionnelles "les blancs jouent et font mat en trois coups" ou "les blancs jouent et font nulle", et il affirmait que c'était à la base du succès des Popov: "Quand vous jouez aux échecs, vous n'avez pas à côté de vous un Père Noël qui vous indique ce qu'il faut faire." C'était très matérialiste dialectique et athée, mais ça me paraissait plein de sens. Ça ne m'a absolument pas aidé à cesser d'être le joueur d'échecs archi-nul que je suis toujours, mais j'ai quand même retenu la leçon et je ne vous dirai pas ce qu'il faut faire sur la grille du jour, na. Faudra que vous le trouviez tout seuls. Je ne vous donne qu'un indice: si vous ne remarquez rien de particulier sur cette grille, ben ça veut dire que vous n'y atteindrez pas l'optimum. Et l'air de rien, vous dire ça, c'est déjà vous aider beaucoup!

Bon, résolvons cette grille "juillet" de façon classique. C'est exactement ce qu'il faut faire... sauf que.

La grille comporte 42 cases. Donc, si on en sacrifie deux (bleues) au départ pour initier la série de coups gagnants (jaunes), il va en rester quarante, qui est égal à un multiple de trois majoré de un. Par conséquent, après la série illimitée de coups gagnants (jaunes), il faudra achever la prise complète de la grille sur un polygone convexe dont le nombre de cases sera lui-même égal à un multiple de trois majoré de un, autrement dit un heptagone.

Et juste avant ce dernier coup (qui prendra le polygone convexe en bleu), il faudra prendre trois cases (en jaune, donc) dans un pentagone marié à ce polygone final (en application du fameux théorème de l'avant-dernier coup).

Rien de plus classique, n'est-ce pas?

Où peut-on trouver sur cette grille un heptagone marié à un pentagone? Par exemple là... Allez, pour le même prix, je vous dessine carrément tout le cavexe:



Bien bien bien, nous avons une stratégie à notre disposition, il va seulement falloir ne pas se laisser empistrouiller par les deux quadrilatères 18, 19, 20, 25 d'une part, 29, 30, 35, 36 d'autre part.

Allons-y gaiement: 19 2 (en bleu), 17 0 26 (et un quadrilatère de zigouillé, un!), 15 29 36 (et un autre quadrilatère de zigouillé, ouf), 32 41 (en jaune), et zou, nous avons dessiné l'inverse du cavexe que nous visons:



Yapuka terminer comme prévu sur le cavexe visé: 31, 37, 4, 12.



Bon, ben c'est parfait, plus orthodoxe tu meurs: deux cases bleues sacrifiées au début, un polygone convexe sacrifié au dernier coup, tout le reste en cases jaunes, c'est-il pas un bel optimum de cases jaunes, ça madame?

Eh bien non! On peut faire mieux!

Je vous avais bien dit que si l'on ne remarquait rien de particulier sur cette grille on n'y atteindrait pas l'optimum...

Qu'aurait-il fallu remarquer?

L'intégralité du raisonnement publié dans le post précédent était valide, sauf une conclusion hâtive, qui aurait quand même été valable sur l'immense majorité des grilles -- raison pour laquelle on a généralement tendance à ne pas s'interroger sur elle.

Le "polygone convexe dont le nombre de cases est égal à un multiple de trois majoré de un", et sur lequel on va jouer le dernier coup (perdant) de la partie, est très généralement un heptagone (il va de soi que ce que je dis là est valide sur une grille à 42 cases, ou 36, ou 48, mais pas sur autre chose, ne me faites pas dire ce que je n'ai pas dit, on n'atteint pas systématiquement le score optimal en terminant sur un heptagone, ça dépend du nombre de cases; si ça ne vous paraît pas évident, révisez les pages précédentes). Très généralement, mais dans quelques cas rares et particuliers, comme sur cette grille "juillet" qui nous occupait hier, il peut parfois être avantageusement remplacé par un quadrilatère.

7 = 2 * 3 + 1, certes, mais 4 = 1 * 3 + 1...

Ben ouais, ça tombe sous le sens... Enfin, pas tant que ça, en fait. Par exemple, sur la grille qui nous occupe, il y a deux quadrilatères, et un seul des deux (18, 19, 20, 25) peut être employé pour jouer le dernier coup d'une partie à score optimal, et cela aussi tombe sous le sens: parce que lui seul est marié à un pentagone, indispensable en vertu du théorème de l'avant-dernier coup dont je ne soulignerai jamais assez l'importance.

Et en plus, ce n'est pas tout: pour atteindre un score optimal en terminant sur un quadrilatère, il faut non seulement un quadrilatère (toutes les grilles n'en comportent pas, loin de là), un quadrilatère marié à un pentagone (et c'est assez rare; regardez avec quoi est marié le quadrilatère 29, 30, 35, 36 de la même grille: un octogone, un hexagone et deux heptagones), mais en plus, en amont de ce couple quadrilatère-pentagone déjà fort rare, il faut encore pouvoir jouer un coup gagnant, ce qui n'est guère possible que si le pentagone dont nous venons de parler est lui-même marié à un autre pentagone. Et avant cet antépénultième coup gagnant, il faudra encore trouver un troisième coup gagnant, ce qui n'est pas nécessairement évident non plus. Bref, un score optimal s'achevant sur un quadrilatère exige la réunion de plein plein de conditions toutes rares... Autant dire que ça n'arrive pratiquement jamais -- raison pour laquelle je n'en ai pratiquement jamais évoqué la possibilité dans les premières pages de ce fil, ça vous aurait embrouillés (mais maintenant vous êtes de grands garçons, et je peux vous dire des choses que je n'aurais pas dites aux élèves de sixième).

Ben sur la grille "juillet", par exception, toutes ces conditions invraisemblables sont réunies, et ça mène donc à la construction d'un cavexe... relativement évident une fois qu'on sait qu'il est là:



Eeeh ben oui, ce n'était même pas caché: le quadrilatère 18, 19, 20, 25 est marié au pentagone 10, 11, 19, 20, 21, lui-même marié au pentagone 4, 5, 10, 11, 12, lui-même marié à un troisième pentagone (à cheval sur les bords inférieur et supérieur et qui pour cette raison ne se voit pas beaucoup) 37, 38, 3, 4, 5. Et une fois qu'on a repéré toutes ces circonstances vraiment très très très particulières, ben faudrait vraiment être une moule pour n'avoir pas idée d'achever le cavexe par les cases 26, 30 et 36. Et voilà, comme disent les Anglais.

Bon, OK, c'était possible, mais fallait vraiment le voir, c'était vraiment la seule et unique possibilité d'obtenir le score optimal sur cette grille, allez-vous me dire? Que nenni, vous n'aurez même pas cette circonstance atténuante: ce cavexe est remarquablement concis, vertical et filiforme, mais ce n'est pas le seul exploitable, et mon solveur (qui adore humilier les simples mortels) en a repéré pas moins de quatre un peu plus massifs et nonobstant tout à fait exploitables:



Donc, non non non, pas d'excuse, la solution d'hier, qui s'achevait sur un heptagone, ne peut pas prétendre qu'elle est quand même "pas si mal que ça": vu qu'elle ne représentait pas l'optimum, elle ne pouvait absolument pas prétendre être une solution "honorable", elle était erronée et elle vaut la note de zéro tout rond, nyark nyark nyark.

Solutions complètes un peu plus tard (voire nettement plus tard).

Et voici donc des solutions pour la grille "juillet", l'une des rares grilles sur lesquelles le score optimal est égal au nombre de cases diminué de seulement six cases: deux pour initier la série de coups gagnants, et un simple quadrilatère au dernier coup de la partie.

Solutions complètes:

Ça se tire, les aminches! Il n'y a plus que cinq grilles de mon inventaire que je n'aie pas encore traitées, et parmi elles, il n'y en a plus qu'une que j'aie classée comme de "difficulté moyenne". Eh bien, nous allons nous en occuper aujourd'hui.

Or donc, le problème du jour sera la grille "vendredi".



Je viens de la résoudre en deux coups de cuiller à pot, a priori ça n'a pas l'air bien malin. Bon courage.

Je traîne pour vous donner les solutions de la grille "vendredi", mais c'est parce qu'elles sont très nombreuses, trop même, avec des cavexes parfois très inutilement massifs, et que plutôt que de vous en faire un inventaire exhaustif j'essaye au moins de m'assurer que je n'en ai raté aucune qui soit vraiment élégante. Perfectionnisme quand tu nous tiens...

Vu que c'est une grille de 42 cases, ça veut dire qu'il faut terminer sur un heptagone marié à un pentagone (j'ai la flemme de vous le réexpliquer ce coup-ci, cherchez dans les épisodes précédents), or les cinq heptagones de cette grille remplissent cette condition, vous pouvez vérifier. Rien d'étonnant, dans ces conditions, que les solutions abondent et qu'il ne leur soit pas nécessaire d'être concises ni élégantes.

Je suis décidément à la bourre, et je ne viendrai pas à bout de la grille "vendredi" aujourd'hui, tellement les solutions valides y abondent. Voici quand même, pour vous faire patienter, une petite collection de cavexes valides et intéressants, tous exploitables pour aboutir à une solution optimale (deux cases isolées bleues, onze coups gagnants jaunes, un heptagone final bleu):



Je vous les ai classés en cinq rangées, chaque rangée étant consacrée à un heptagone particulier. Pour chacun d'entre eux, je vous ai mis au moins un cavexe horizontal et un cavexe vertical, et j'ai parfois ajouté des variantes qui m'ont paru intéressantes.

Et l'air de rien, tout ça, c'était énormément de travail... donc je n'ai pas trop scrupule à être à la bourre.

Solutions complètes demain. S'il plaît à Dieu.

Je me casse le tronc à essayer de faire un tour complet des solutions possibles sur chaque grille étudiée -- pour deux raisons. La première, c'est que je me conforme à la méthode d'un copain généralement de très bon conseil:

René Descartes a écrit:faire partout des dénombrements si entiers et des revues si générales, que [l'on puisse être] assuré de ne rien omettre.

... et la seconde, c'est de vous inciter à la persévérance. Quand vous avez repéré un polygone final ayant le nombre de cases qui va bien, et marié à un pentagone comme il se doit pour atteindre le score optimal théorique, il reste à élaborer un cavexe rondouillard sur cette base. C'est rarement facile et ce n'est pas toujours possible, hélas, c'est pourquoi je crois important de ressasser aux débutants que même si ça n'est pas toujours possible c'est quand même possible dans de très nombreux cas (dans la plupart, à vrai dire), raison pour laquelle il faut s'acharner beaucoup de peur de se décourager trop tôt. Je sais, c'est prêchi-précha, ce que je vous dis là, c'est ma mentalité de vieux cureton qui ressort, mais les vieux curetons ne disent pas que des conneries et j'en ai connu qui m'ont vraiment aidé à construire mon âme comme j'essaie de vous aider à construire la vôtre, parfaitement (quoi, vous n'aviez pas encore compris que ce fil était un long prêche pour les quatre règles de la raison du père Descartes? c'était pourtant bien mal caché...).

Par ailleurs, une erreur de débutant (que j'ai commise bien des fois, évidemment) est de se dire "pisque ça n'a pas l'air facile avec ce polygone final-ci, je vais le laisser tomber et essayer avec ce polygone final-là". Ce n'est pas forcément une bonne stratégie de papillonner ainsi, ça dépend des grilles. Disons pour vous donner une idée que n'importe lequel des treize cavexes que je vous ai montrés hier pouvait être trouvé en environ cinq minutes; si vous consacrez une minute trente à chacun d'entre eux dans l'espoir d'en rencontrer un facile, vous travaillerez 13 * 1,5 = une vingtaine de minutes sans obtenir de résultat, alors qu'en vous acharnant sur une seule idée vous auriez trouvé une solution (pas forcément élégante) en quatre fois moins de temps. C'est une des choses que l'on apprend en jouant à ce jeu: à jauger au doigt mouillé combien de temps il faut s'acharner sur une idée médiocre, mais valide, avant de se mettre en quête d'une meilleure, laquelle, même si elle existe, n'est pas forcément plus facile à trouver. C'est tout un art, et comme tous les arts, il demande de la pratique, de l'entraînement et de la persévérance et il va arrêter de nous faire chier le vieux cureton?

Bref. Je reviens aux cavexes publiés hier soir. Ils sont de qualité inégale. Le 1a, le 3a et surtout le 4a sont vraiment concis et par là-même élégants, ce sont mes préférés. Le 3a bis est assez quelconque, mais je l'ai trouvé (avec mes années d'entraînement) au bout de seulement quelques dizaines de secondes d'acharnement et vous verrez que vous finirez par en être capables vous aussi, petits scarabées. Et ne méprisez pas le 2b ni même le 1b_bis: même s'ils sont très massifs, obèses, "gorditos" comme on dirait en Bolivie, ils présentent le gros avantage d'être bien carrés et donc très faciles à photographier mentalement, donc ils représentent une autre forme d'élégance. Quant aux autres, ben ma foi ils ont l'énorme mérite d'exister (comme mon 3a bis), et je pense que vous pouvez accepter comme philosophie de l'existence que la meilleure solution est la première qui marche (philosophie inspirée du petit monde linuxien, où l'on discute à n'en plus finir des mérites comparés de quantité d'outils complètement interchangeables et disposant pourtant chacun de petites chapelles de fanatiques qui ne voudraient en essayer un autre sous aucun prétexte).

J'arrête là mon prêche, même que c'est pas dommage. C'est égal, méditez tout ceci en votre coeur, mes bien-aimés, je vous assure que ça pourra vous servir dans des contextes très différents.

Solutions complètes (et abondantes):

A part ça, bonne fête du Travail.

Le problème du jour sera la grille "blancheneige".



Je tue tout de suite le suspense: cette grille, que je vous ai classée à bon droit comme "difficile", aurait aussi pu être désignée comme "particulière", tout comme la grille "juillet" que nous avons vue il y a rien de temps et pour la même raison: l'optimum y est atteint en terminant sur un quadrilatère (marié avec un pentagone, évidemment, en vertu du théorème de l'avant-dernier coup, reportez-vous aux épisodes précédents).

C'est la même chose, sauf que c'est plus dur. Ou pas, d'ailleurs...

Ce qui est sûr, c'est que sur la grille "juillet", nous avions trouvé pas moins de cinq cavexes inversibles. Eh bien, sur la grille "blancheneige" qui nous occupe aujourd'hui, vous n'aurez pas cet embarras du choix, car elle entre dans la catégorie ra-ris-sime des grilles qui n'admettent qu'un seul cavexe inversible.

Lequel, bien évidemment, ne saute pas aux yeux, perdu qu'il est au milieu des milliers de milliards de solutions envisageables. Allez, je vais être honnête: moi, je ne l'ai pas vu, j'ai crié grâce... et c'est seulement en regardant travailler mon solveur que je me suis rendu compte que cette solution existe et est unique.

Mais ça, ça ne démontre pas que c'est difficile, ça démontre seulement que je suis un âne bâté.

Aussi, je vous dis comme tous les bons pédagogues: "Faites ce que je dis, ne faites pas ce que je fais." Vous, ne baissez pas les bras. Demandez-vous, avec rigueur et méthode: où que c'est-il que je peux jouer le dernier coup? et l'avant-dernier? et l'antépénultième? et celui d'avant? et celui d'encore avant? Dans l'immense majorité des cas, sur la grille "blancheneige", la réponse à chacune de ces questions est unique ou presque (il suffit de très peu raisonner pour éliminer les hypothèses foireuses).

Donc si vous raisonnez ri-gou-reu-se-ment vous devriez tomber directement sur la solution miraculeuse qui va bien, qui atteint l'optimum, qui est élégante et efficace... La démarche intellectuelle est beaucoup plus proche de l'enquête de police minutieuse et méthodique que de l'intuition géniale. Ne vous prenez pas pour Sherlock Holmes, drafaillez afec méthôde et distzipline... comme l'inspecteur Derrick, allez: observez les indices, interrogez les témoins, relevez les contradictions... et vous y arriverez tout droit. Cette grille n'est difficile que si on la croit telle, comme j'ai eu la sottise de le faire. Croyez que le résultat est à votre portée et vous l'atteindrez. Bêtement, c'est-à-dire de la seule façon intelligente qui soit à votre disposition en l'occurrence.

Bon, allez, entamons la résolution de cette fameuse grille "blancheneige" avec ordre, méthode et discipline... et avec plein d'images sous spoiler pour vous faire honte de n'avoir pas trouvé la solution tous seuls tellement elle était visible... non, pas comme le nez au milieu de la figure, mais vraiment pas plus difficile à repérer que Mars et Jupiter dans un ciel étoilé: avec un minimum de connaissances, on y arrive sans peine (vous dit Petitagore qui n'y est pas arrivé tout seul... mais ma nullité n'excuse nullement la vôtre, bande de petits salopards!).

Primo, sur quel polygone faut-il terminer la résolution de cette grille? Je vous l'ai déjà dit dans le post précédent, mais maintenant je l'explique (une énième fois...). Cette grille a 42 cases. Comme au départ il faudra que j'en sacrifie deux, ce qui est presque universellement le cas, il m'en restera 40, or 40 = 13 * 3 + 1, un multiple de trois majoré de un, donc le nombre de cases du polygone final devra être... la même chose: un multiple de trois majoré de un. Donc il devra avoir sept cases (= 2 * 3 + 1) ou, mieux, quatre cases (= 1 * 3 + 1), ce devra être un heptagone ou, mieux, un quadrilatère.

Il est rare qu'on puisse atteindre le score optimal en terminant sur un quadrilatère; rare, mais pas exclu. Déjà, y a-t-il un quadrilatère sur cette grille? Mais ouvrez vos yeux, pétard!

Vous auriez dû le voir...:

Il y a deux quadrilatères sur cette grille, mais un seul nous intéresse. Lequel?

Agnan?

-- Çui qu'il est marié avec un pentagone, m'sieur.

Pourquoi?

-- A cause du théorème du dernier coup, m'sieur.

A cause du théorème de l'avant-dernier coup, bougre d'âne! Mais putain, vous allez finir par me l'apprendre, ce putain de théorème de mes couilles, sacré nom de Dieu de bordel de pute à queue!

Bon, on avance. Et où qu'il est-il, le quadrilatère marié sur un pentagone?

Hein?

-- Y en a pas, m'sieur.

Non mais c'est pas vrai, mais quelle bande de nullards...

Et ça, c'est une photo du yéti?:

Ah ben ouais, fallait faire l'effort de réfléchir. Pauvres chéris, vraiment je vous persécute.

Et en amont de ce quadrilatère marié à un pentagone, est-ce qu'on peut prendre trois cases?

Je ne vous le demanderais pas si la réponse n'était pas oui, alors trouvez-moi où, pétard!

Eh ben ouais, évidemment...:

Bon, jusque là j'ai vraiment été d'une indulgence extrême, mais je vous jure que si vous ne me dites pas tous et immédiatement quel coup on peut jouer en amont de ce coacervat, je demande votre exclusion définitive du cours de Triancey partrois, et j'exigerai de voir vos parents individuellement pour qu'ils sachent bien quelle bande de fumistes et de nullards vous êtes.

Alors, vous me le trouvez, ce coup gagnant qu'on peut jouer en amont, bordel?

Ah, quand même!:

Bon, là, j'admets, il y a une difficulté, oh la la que c'est difficile, en amont de ce coacervat vous avez le choix entre deux coups gagnants, tout ça, oui. Deux coups possibles. Vous allez évidemment commencer par le mauvais qui ne vous mènera à rien (si vous cliquez sur 23 pour prendre 23, 24 et 32, eh bien vous ne pourrez pas jouer un coup gagnant en amont de ça) et donc vous aurez peut-être seuls l'idée géniale, après avoir échoué sur la première possibilité, de tester la seconde... Prenez votre temps, j'ai que ça à foutre...

Ils y sont arrivés, c'est inespéré!:

Peste, vous m'impressionnez. En moins d'une demi-heure, vous avez réussi à repérer les quatre seuls coups gagnants qu'on pouvait jouer en amont du quadrilatère final. Ah, bel effort, chapeau. Donc des champions comme vous vont peut-être réussir à me trouver en moins d'une heure le coup pas complètement intuitif qu'il faudrait jouer maintenant pour achever le cavexe? Je serai indulgent, c'est pas tout à fait rigoureusement complètement évident, mais je vous assure que c'est quand même à la portée du concierge du collège, même quand il rentre bourré à cinq heures du mat, donc vous allez peut-être y arriver aussi. Mais surtout, prenez votre temps.

Aaaaaa y est, ils ont trouvé!:

Je vous ai un peu houspillés, soit, et même je veux bien admettre qu'il était pas tout à fait évident, ce cavexe, vu que l'espèce de faux tenon constitué par les cases 5 et 13 empêche de lui conférer ce sympathique aspect rondouillard qu'ont habituellement les cavexes inversibles. C'est vrai.

Mais pétard rendez vous compte que le raisonnement vous y menait TOUT DROIT! Tout droit! Vous pouviez pas le rater, c'était un éléphant dans un couloir!

-- Mais vous nous avez dit que vous-mêmes vous ne l'aviez pas vu, m'sieur.

Ta gueule, Agnan. Ce n'est pas fini! Maintenant il faut me trouver une solution complète sur la base de ce cavexe qui nous a demandé tant d'efforts. Donc, au boulot!

Au risque de vous embrouiller, je crois qu'avant de publier les solutions il est intéressant que je vous montre un autre cavexe même s'il n'est pas orthodoxe:



Le cavexe que nous avons élaboré dans le post précédent était inversible mais pas rondouillard (il y avait un faux ensemble tenon-mortaise, les cases 5 et 13 faisant office de tenon, les cases 4, 11 et 12 de mortaise)... eh bien, celui que je vous montre ci-dessus rétablit l'équilibre: car lui, il a beau être rondouillard... il n'est pas inversible.

C'est très curieux, je n'avais encore jamais réfléchi à ce genre de configurations et je me demande s'il serait facile d'en trouver d'autres exemples. Mais j'ai constaté que le solveur passait très souvent par ce cavexe, qu'il atteint le score optimal avec lui aussi facilement qu'avec le précédent, et en plus celui-ci a un aspect rondouillard de très bon aloi.

Cela dit, il n'est pas orthodoxe: pour le construire, il va falloir employer un coup non inversible (par exemple: 29, 20, 21 -- trois coups bleus prenant quatre cases --, 41, 28, 25, 39, 18 -- non inversible --, 22), et si vous l'employez pour aboutir au score optimal, vous devrez symétriquement y jouer un coup comportant un tenon. C'est un de ces cas où mon solveur me laisse pantois par l'élégance des astuces qu'il imagine.

Je vous recommande d'y réfléchir un peu avant de donner votre langue au chat.

Solutions complètes:

Et maintenant, nous allons plancher sur la grille "samedi". Je ne vous dis pas que ce sera le problème "du jour"... car des circonstances familiales totalement indépendantes de mes gamberges triangulo-toriques risquent de m'accaparer un peu dans les jours qui viennent, donc il est possible que ce fil prenne un peu de retard (voyez-y une occasion de réviser les pages précédentes!). Toujours est-il que la grille "samedi", la voici:



Elle a 46 cases, 46 = 2 + 44 (deux cases bleues sacrifiées au début), et 44, c'est un multiple de trois majoré de deux, donc il faut jouer le dernier coup (perdant et donc bleu) sur un polygone convexe dont le nombre de cases sera lui-même un multiple de 3 majoré de deux, c'est-à-dire un pentagone (5 = 1 * 3 + 2) ou, au pis-aller, un octogone (8 = 2 * 3 + 2).

Bref, nous sommes en présence d'une grille "cinq ou huit", espèce maudite ou bénie capable du meilleur (les problèmes élégants) comme du pire (les problèmes aussi ennuyeux qu'inélégants) dont je vous ai déjà pas mal parlé, par exemple dans ce post-ci.

Je tue le suspense: ici, c'est bien sur un pentagone qu'il faut terminer, et ce n'est même pas épouvantablement difficile -- donc ce serait bête de vous décourager tout de suite.

Je reviendrai sur ce fil pour vous donner de petits coups de main avant de vous balancer les solutions complètes... mais je ne vous promets pas d'avoir le temps de le faire aujourd'hui.

Désolé, les copains, je n'ai pas eu beaucoup de temps à consacrer à la grille "samedi", mais elle ne m'a pas paru mériter des réflexions bouleversantes. Pour l'essentiel, sa résolution peut employer seulement deux cavexes inversibles pas horriblement massifs...



... lesquels ne sont ni impossibles à imaginer, ni très évidents (enfin, les cinq derniers coups de la partie, donc les cinq premiers à identifier pour dessiner un cavexe, sont assez évidents, mais pas la suite).

Désolé, je n'ai pas le temps de détailler. Voici les solutions.

Solutions complètes:

Ce fil va probablement s'interrompre quelques jours. A bientôt!

Bonjour les gars et les filles... Ça se tire, vraiment ça se tire, si je ne m'abuse il ne reste que deux grilles sur la série de trente-quatre à partir de laquelle j'ai décidé il y a deux mois de construire tous mes exemples pédagogiques. Quand nous aurons fini tout ça, j'essaierai d'accoucher d'une table des matières et d'un index, et puis surtout je tâcherai de transformer la douzaine de pages de ce fil en une monographie libre de diffusion en PDF (très probablement mise en page avec LaTeX, pour ceux qui connaissent). Mais nous n'en sommes pas encore tout à fait là, et le problème du jour sera la grille "dormeur", de la série "Blanche-Neige et les sept nains".



M'étonne pas que je l'aie répertoriée parmi les grilles difficiles et que je vous l'aie gardée pour la fin. Déjà, c'est une grille à trois quadrilatères (1, 2, 3, 11 contre le bord supérieur; 23, 24, 30, 11, aux environs du centre; et le troisième que vous n'aviez pas vu, bande d'amateurs: 5, 6, 39, 40, réparti sur les bords inférieur et supérieur du tore). Trois quadrilatères, c'est beaucoup, et d'autant plus que, comme la pratique devrait vous l'avoir déjà enseigné, les quadrilatères ont une tendance prononcée à faire foirer tous les efforts des joueurs les plus persévérants. Comme si ça ne suffisait pas, cette grille bizarroïde comporte un ennéagone (et non un nonagone, comme disent les ignorants à qui on n'a jamais enseigné qu'il ne fallait pas mélanger les racines grecques et latines): 2, 3, 13, 4 et 5 contre le bord supérieur du tore, 36 à 39 contre le bord inférieur.

Eh bien, elle a beau être très mal foutue, cette grille (au point que mon solveur la résoud généralement en employant des cavexes "à mortaise", voire des stratégies dissidentes et peu orthodoxes, je vous montrerai), elle est quand même susceptible d'au moins quatre résolutions archi-classiques et académiques, à base de cavexes rondouillards et inversibles de très bon aloi. C'est une grille pour super-pros et je l'ai résolue tout seul, nananère, mais ça m'a quand même pris des dizaines de minutes après des années d'apprentissage, donc si vous en faites autant vous aurez le droit de vous prendre pour des kadors.

Et si vous n'êtes pas assez fanfarons pour vous en croire capables, je rends hommage à votre modestie mais je vous incite quand même à essayer: c'est -- entre autres -- en se cassant les dents sur les grilles très difficiles qu'on apprend à vaincre comme qui rigole les grilles moins difficiles. Bon courage.

Quelques indices pour continuer avec la grille "dormeur".

C'est une grille de 42 cases, donc on peut présumer que le score optimal y est atteint en terminant sur un heptagone: avec deux cases sacrifiées au début comme c'est généralement indispensable, il en reste 40, qui est un multiple de 3 majoré de 1, donc le dernier coup (perdant et bleu) doit être joué sur un polygone convexe dont le nombre de cases est lui aussi un multiple de 3 majoré de 1, donc un heptagone. A vrai dire, on peut être brièvement tenté d'essayer de terminer sur un quadrilatère (4 aussi est un multiple de 3 majoré de 1), d'autant qu'il y a sur cette grille deux quadrilatères mariés chacun à un pentagone et laissant donc l'espoir de jouer à proximité d'eux, dans ce pentagone, un avant-dernier coup gagnant. C'est bien pensé... mais en l'occurrence ça marche pas.

Je ne sais pas si vous avez essayé de dessiner sur cette grille un cavexe rondouillard et inversible avec un joli heptagone dedans, mais c'est vraiment pas de la tarte. Pour abréger vos souffrances, voici ceux que mon solveur a identifiés comme possibles:



A vrai dire, le deuxième, qui ressemble furieusement au premier en un peu moins concis, n'a pas été trouvé par mon solveur mais par votre serviteur -- et il en a bavé pour y arriver, votre serviteur, vous pouvez me croire.

Il est fort possible que ces quatre cavexes soient à peu près les seuls envisageables sur cette grille, mais ils ne constituent quand même pas des passages obligés pour atteindre le score optimal de onze coups gagnants (jaunes). Outre les incompréhensibles cavexes "à mortaise" dont mon solveur s'est fait la spécialité... il reste la possibilité de réfléchir aux stratégies hérétiques évoquées par le sympathique lecteur Jean-Pierre Liégeois de Carpentras dans ce post vieux de plus d'un mois (comme le temps passe). A l'époque, j'avais dénoncé ces stratégies hérétiques comme inutilement compliquées... eh bien, par exception, sur cette grille-ci, elles mènent réellement à des solutions plus faciles à trouver.

Mais je ne vous en dis pas plus, il faut quand même que vous bossiez un peu.

Et voici les solutions pour la grille "dormeur".

Commençons par les solutions orthodoxes:

On pourrait en rester là. Mais mon solveur me rend assez de services pour que je ne censure pas sa créativité, et l'honnêteté me force à signaler qu'au lieu de terminer de façon classique et orthodoxe sur un heptagone, il choisit le plus souvent (me demandez pas pourquoi) de terminer sur un pentagone en sacrifiant deux nouvelles cases en cours de route... C'est bizarre, mais ça mène bien au même score optimal: au lieu de sacrifier deux cases au début et un heptagone à la fin (2 + 7 = 9), il sacrifie deux cases au début, deux cases en cours de route et un pentagone à la fin, et atteint donc le même score optimal (2 + 2 + 5 = 9 aussi). C'est quand même, à mon sens, nettement moins élégant: on atteint le même nombre de coups gagnants et donc le même score optimal, mais on ne réalise pas une série ininterrompue de coups gagnants -- performance qui, à mon avis, comble davantage d'aise les esprits mathématiques bienveillants qui gouvernent le monde et veillent sur nous. Mais ce n'est que mon opinion de dévot de la logique, je suis bien incapable de vous démontrer que les dits esprits sont du même avis que moi sur cette question.

Berk les vilaines solutions hérétiques:

Bon, ben si on renonce à l'exigence d'une série ininterrompue de coups gagnants, pourquoi ne pas essayer aussi de terminer sur un hexagone en ayant sacrifié trois cases en amont (2 + 1 + 6 = 9, toujours 9...). C'est ce que j'ai fait et, honnêtement, j'y suis arrivé comme qui rigole, alors que l'élaboration de ma solution orthodoxe m'avait demandé je ne sais combien de dizaines de minutes d'essais infructueux. En plus, ça n'est pas désagréable à l'oeil:



Si vous êtes un taliban du Triancey "partrois", vous condamnerez au bûcher toutes les solutions ne comportant pas une série ininterrompue de coups gagnants. Si au contraire vous estimez que peu importe que le chat soit noir ou blanc du moment qu'il atteint le score optimal, ben vous admettrez ces solutions et il faudra peut-être recaler cette grille de la catégorie "difficile" à "difficulté moyenne"... Je vous laisse choisir et je me bornerai à vous interdire formellement la crémation des hérétiques: je suis parfois partisan de l'orthodoxie, mais jamais du bûcher.

Solution hérétique à ne pas montrer aux talibans:

Le problème du jour sera la grille "dimanche", avec laquelle, croyez-le si vous-voulez, nous achèverons de traiter la liste des 34 grilles que j'ai mises à votre disposition à titre pédagogique. Mon Dieu, mon Dieu, que de chemin parcouru.



Je vous avais classé cette grille dans la catégorie "cinq ou huit", mais c'était à l'époque où vous étiez des débutants, et au niveau où désormais vous vous trouvez presque tous (tousse, tousse), vous pouvez considérer que c'est une grille très facile. Y a pas de piège, appliquez la méthode et crac boum vous en viendrez à bout.

Solutions... plus tard, probablement pas avant demain.

Non, elle n'était vraiment pas bien compliquée, cette grille "dimanche".

Bon, finissons-en avec la routine (ça commence sérieusement à me gonfler de répéter toujours la même chose, pas vous?).

Cette grille comporte 40 cases, j'en sacrifie deux (bleues) au début, il en reste 38, et 38 étant un multiple de 3 majoré de deux, il faut jouer le dernier coup sur un polygone convexe dont le nombre de cases soit lui aussi un multiple de 3 majoré de deux, c'est-à-dire un pentagone (ça pourrait aussi être un octogone, mais ce serait moins bon puisque ça ferait trois cases jaunes de moins). Par ailleurs, le théorème de l'avant-dernier coup impose que l'avant-dernier coup d'une partie à score optimal (ou du moins à score optimal "classique") soit joué sur un pentagone marié (par deux cases) avec le polygone convexe final.

Donc nous cherchons sur cette grille deux pentagones mariés. Ouf. C'est rasoir, la routine, non? C'est nécessaire d'en passer par là, mais peut-être moins de le répéter sempiternellement...

Bon. Où y a-t-il deux pentagones mariés sur cette grille? En fait, il n'y en a pas deux, mais trois: le pentagone 19, 20, 26, 27, 28 est marié à droite par les cases 20 et 28 au pentagone 20, 21, 22, 28, 29, mais aussi à sa gauche par les cases 26 et 27 à un troisième pentagone coupé en deux de part et d'autre des deux bords verticaux du tore, le pentagone 31, 39, 26, 27, 32.

Eh bien, entamons notre cavexe par ces trois pentagones, et il est clair qu'il n'y a plus qu'à ajouter les cases 23, 30 et 24 pour achever le cavexe:



Honnêtement, c'était fastoche pour nous, qui sommes certes d'humbles mortels mais qui avons des yeux pour voir. Mon solveur, lui, n'a pas d'yeux, et c'est à tâtons dans les sombres recoins de la mémoire vive de mon ordinateur qu'il a dû chercher à dessiner d'autres cavexes valides. Il en a quand même trouvé six, dont pas un n'est aussi élégant que le premier:



Tous sont utilisables pour aboutir à un score optimal, bien entendu.

Donc, à vous de vous en inspirer pour aboutir vous-mêmes au score optimal. Je publierai des solutions complètes... un peu plus tard, cet après-midi ou ce soir.

Bon. Eh bien, voici comme promis les solutions de la grille "dimanche".

Solutions complètes:

Et voilà... Nous sommes venus à bout des trente-quatre grilles que j'avais préparées dès le départ. Nous avons défini ce qu'était un optimum, un cavexe, un optimum classique, nous avons démontré les quatre théorèmes (premier coup, deuxième coup, troisième coup, avant-dernier coup), nous avons résolu des grilles s'achevant sur un pentagone, un hexagone, un heptagone, un quadrilatère, un octogone, un couloir, un n'importe-quoi un peu bizarre... Nous avons vu des grilles où les solutions élégantes abondent, d'autres où il n'y a aucune solution élégante. Nous avons vu qu'il y a des grilles difficiles qui admettent pourtant plusieurs solutions, et des grilles qui n'admettent guère qu'une solution perdue parmi des milliers de milliards de combinaisons et qui sont quand même assez faciles avec un peu de méthode...

Et ça nous a servi à quoi, tout ça?

Franchement, je ne le sais pas, mais j'ai quand même l'absolue conviction que la réponse n'est pas "à rien".

Je ne sais pas pourquoi les humains -- enfin, certains humains que sur ce forum on appelle généralement des zèbres -- tiennent absolument à se triturer les méninges pour établir à quoi ressemble la vérité dans tel ou tel domaine raccordé à rigoureusement rien de concret. Mais c'est comme ça. Comme dit le scorpion dans la fable du scorpion et de la grenouille: "Que veux-tu, c'est dans ma nature."

Je ne sais pas trop ce que je vais faire de tout ça maintenant. Une table des matières, un index thématique, une compilation, ce genre de trucs... oui, c'est probable. Mais après?

En tout cas, je n'ai pas été mécontent de le faire.

Je songe vaguement à transformer les onze pages de ce fil en une petite monographie libre de diffusion, à usage des matheux des générations futures... et à cette fin, voici déjà un index chronologique. Je crains que ça n'intéresse que moi, mais vous pouvez quand même vous en servir, vous avez ma bénédiction.

Mar 24 Fév 2015 - 0:00
Présentation générale - Concept de réactions en chaîne

Mar 24 Fév 2015 - 16:34
Présentation technique de la version "partrois"

Mer 25 Fév 2015 - 10:54
Explication de l'objectif: le maximum de cases jaunes

Mer 25 Fév 2015 - 11:54
Pourquoi le nombre de cases est toujours pair

Mer 25 Fév 2015 - 13:30
Aspect visuel des optima

Jeu 26 Fév 2015 - 10:30
Théorèmes du premier, deuxième et dernier coup

Jeu 26 Fév 2015 - 16:17
Les scores optimaux les plus courants

Ven 27 Fév 2015 - 12:32
Théorème de l'avant-dernier coup - Notion de cavexe - Résolution détaillée de la grille "janvier"

Dim 1 Mar 2015 - 17:29
Grille "chirac": insoluble de façon classique car dépourvue de pentagone

Mar 3 Mar 2015 - 9:44
Interrogation sur le nombre de grilles différentes

Mar 3 Mar 2015 - 16:42
Evaluation (erronée) du nombre de grilles

Mer 4 Mar 2015 - 17:32
Grille "decembre"

Ven 6 Mar 2015 - 16:00
Notion de cavexe inversible

Sam 7 Mar 2015 - 9:22
Amorce de méthode pour déterminer avec certitude si deux grilles sont différentes

Sam 7 Mar 2015 - 18:59
Un réseau d'hexagones sur un tore

Sam 7 Mar 2015 - 19:23
La façon la plus simple d'inscrire des hexagones sur un tore

Dim 8 Mar 2015 - 0:47
Digression: unifier la surface des cases

Dim 8 Mar 2015 - 12:13
Les trente-quatre grilles classées par difficulté

Lun 9 Mar 2015 - 10:29
Grille "mai" - Facile parce qu'insoluble de façon classique

Lun 9 Mar 2015 - 23:42
Exemple de deux grilles différentes alors que leurs descriptifs concis seraient semblables

Mar 10 Mar 2015 - 9:45
Grille "octobre" - En quoi les quadrilatères sont gênants

Mer 11 Mar 2015 - 9:13
Grille "atchoum"

Mer 11 Mar 2015 - 12:15
Estimation de la complexité de la résolution d'une grille

Mer 11 Mar 2015 - 16:50
Solutions de la grille "atchoum" sans les cinq derniers coups

Jeu 12 Mar 2015 - 9:51
Grille "lundi"

Ven 13 Mar 2015 - 9:59
Gamberges sur le caractère intelligent ou non des solutions bizarroïdes

Mar 17 Mar 2015 - 9:03
Grille "mars"

Mar 17 Mar 2015 - 11:23
Difficultés pédagogiques: faire appliquer une méthode non comprise

Mer 18 Mar 2015 - 10:20
Caractère inversible ou non d'un cavexe; concavité, convexité

Mer 18 Mar 2015 - 16:49
Tenons et mortaises

Jeu 19 Mar 2015 - 10:07
Les cavexes à mortaise

Ven 20 Mar 2015 - 9:20
Grille "avril" - Cinq rangées horizontales

Ven 20 Mar 2015 - 11:43
Obtenir l'optimum de façon non classique (méthode Jean-Pierre Liégois de Carpentras)

Dim 22 Mar 2015 - 10:03
Grille "juin"

Dim 22 Mar 2015 - 18:17
Le cavexe le plus concis est-il toujours le meilleur?

Lun 23 Mar 2015 - 8:41
Grille "aout"

Mar 24 Mar 2015 - 8:58
Grille "novembre"

Mar 24 Mar 2015 - 23:19
Solutions orthodoxes mais bizarres, dont un cavexe torsadé - Se montrer "fort contre Dieu"

Jeu 26 Mar 2015 - 0:00
Grille "septembre" (effroyablement difficile, soluble uniquement avec des cavexes "à mortaise") - Les vignettes Panini

Jeu 26 Mar 2015 - 14:25
Les grilles "cinq ou huit" - Grille "prof"

Jeu 26 Mar 2015 - 20:04
Pourquoi une grille "cinq ou huit" peut être la meilleure et la pire des grilles - Chercher un chat noir dans une pièce sombre sans savoir s'il y est

Ven 27 Mar 2015 - 9:46
Grille "grincheux"

Sam 28 Mar 2015 - 10:28
Grille "joyeux" - Les multiples façons de terminer en sacrifiant huit cases

Dim 29 Mar 2015 - 18:41
Les solutions extraterrestres

Lun 30 Mar 2015 - 17:43
L'horloger de Voltaire - Une petite réplique à Richard Dawkins

Mer 1 Avr 2015 - 0:07
Les pouvoirs paranormaux de Triancey

Jeu 2 Avr 2015 - 9:57
Grille "simplet"

Ven 3 Avr 2015 - 10:30
Grille "timide" - Cavexe horizontal sur grille à structure horizontale

Sam 4 Avr 2015 - 11:56
Grille "degaulle" - Grille "inratable": multiplicité de solutions

Mar 7 Avr 2015 - 9:51
Grille "pompidou" - Une seule solution, qui tombe donc sous le sens

Mer 8 Avr 2015 - 10:01
Grille "mercredi"

Ven 10 Avr 2015 - 8:57
Le Saint-Graal du Triancey partrois (théorie): une seule case bleue sur toute la grille

Sam 11 Avr 2015 - 0:16
Structure informatique des descriptifs des grilles

Sam 11 Avr 2015 - 10:29
Les scripts Unix de production des grilles

Sam 11 Avr 2015 - 16:55
La grille "Saint-Graal"

Mar 14 Avr 2015 - 9:54
Grille "mardi" (avec un exemple de cavexe qu'on peut dessiner mais non employer)

Mar 14 Avr 2015 - 17:11
Digression métaphysique - Pourquoi la perfection ennuie Dieu (conversion de Saint Paul)

Jeu 16 Avr 2015 - 10:36
Grille "giscard" (exemple heureusement rare d'une grille vraiment ennuyeuse; c'est un "cinq ou huit" se terminant sur huit sans aucune élégance)

Ven 17 Avr 2015 - 10:42
Grille "jeudi" - De l'utilité de la foi en la victoire

Dim 19 Avr 2015 - 9:33
Grille "mitterrand"

Lun 20 Avr 2015 - 10:38
Grille "sarkozy"

Mer 22 Avr 2015 - 9:22
Grille "hollande" (particulièrement facile)

Jeu 23 Avr 2015 - 10:17
Grille "fevrier" - Très difficile - et vexante quand on voit qu'il y existait quand même une solution simple

Lun 27 Avr 2015 - 9:11
Grille "juillet" - "Particulière" (on peut la terminer sur un quadrilatère)

Lun 27 Avr 2015 - 18:20
Résolution erronée (et apparemment irréprochable) de la grille "juillet" - Exemple détaillé, donc pédagogique

Mer 29 Avr 2015 - 9:52
Grille "vendredi" - Difficile en raison de l'abondance des solutions

Sam 2 Mai 2015 - 9:23
Grille "blancheneige" - Difficile mais de solution évidente pour des esprits méthodiques - Exemple détaillé

Dim 3 Mai 2015 - 19:33
Cas rare d'un cavexe non orthodoxe (non inversible) et pourtant compréhensible

Lun 4 Mai 2015 - 8:58
Grille "samedi"

Jeu 7 Mai 2015 - 8:53
Grille "dormeur" - Susceptible de solutions hérétiques

Sam 9 Mai 2015 - 8:46
Grille "dimanche"

Encore un post principalement à l'usage de votre serviteur et de sa monographie future: un inventaire des grilles de démonstration, indiquant leur difficulté et renvoyant aux moments où l'on a discuté de chacune d'entre elles.

Les douze mois de l'année

Grille janvier - Très facile (et particulièrement pédagogique)
Discussion en date du Ven 27 Fév 2015 - 12:32

Grille février - Difficile (et même très -- mais il existe quand même une solution simple)
Discussion en date du Jeu 23 Avr 2015 - 10:17

Grille mars - Difficulté moyenne
Discussion en date du Mar 17 Mar 2015 - 9:03

Grille avril - Difficulté moyenne (on peut noter sa structure très horizontale)
Discussion en date du Ven 20 Mar 2015 - 9:20

Grille mai - Facile (mais insoluble de façon classique)
Discussion en date du Lun 9 Mar 2015 - 10:29

Grille juin - Difficulté moyenne
Discussion en date du Dim 22 Mar 2015 - 10:03

Grille juillet - Particulier (on peut la terminer sur un quadrilatère)
Discussion en date du Lun 27 Avr 2015 - 9:11

Grille aout - Difficulté moyenne
Discussion en date du Lun 23 Mar 2015 - 8:41

Grille septembre - "Cinq ou huit" (effroyablement difficile, soluble uniquement avec des cavexes "à mortaise")
Discussion en date du Jeu 26 Mar 2015 - 0:00

Grille octobre - Facile
Discussion en date du Mar 10 Mar 2015 - 9:45

Grille novembre - Difficulté moyenne
Discussion en date du Mar 24 Mar 2015 - 8:58

Grille decembre - Difficile (la difficulté est liée au fait qu'on peut se braquer sur une hypothèse de résolution irréalisable)
Discussion en date du Mer 4 Mar 2015 - 17:32

Blanche-Neige et les sept nains

Grille blancheneige - Difficile (mais de solution évidente pour des esprits méthodiques)
Discussion en date du Sam 2 Mai 2015 - 9:23

Grille atchoum - Facile
Discussion en date du Mer 11 Mar 2015 - 9:13

Grille dormeur - Difficile (et susceptible de solutions hérétiques)
Discussion en date du Jeu 7 Mai 2015 - 8:53

Grille grincheux - Difficulté moyenne
Discussion en date du Ven 27 Mar 2015 - 9:46

Grille joyeux - Difficulté moyenne (multiples façons de terminer en sacrifiant huit cases)
Discussion en date du Sam 28 Mar 2015 - 10:28

Grille prof - "Cinq ou huit" (typique de ce genre de grilles)
Discussion en date du Jeu 26 Mar 2015 - 14:25

Grille simplet - Difficulté moyenne
Discussion en date du Jeu 2 Avr 2015 - 9:57

Grille timide - Difficulté moyenne (structure horizontale sur laquelle un cavexe "en ruban" est possible)
Discussion en date du Ven 3 Avr 2015 - 10:30

Les présidents de la Ve République

Grille degaulle - Difficulté moyenne (grille "inratable": multiplicité de solutions)
Discussion en date du Sam 4 Avr 2015 - 11:56

Grille pompidou - Difficulté moyenne (guère qu'une solution, mais qui tombe donc sous le sens)
Discussion en date du Mar 7 Avr 2015 - 9:51

Grille giscard - "Cinq ou huit" (grille ennuyeuse; on ne peut que terminer sur huit sans aucune élégance)
Discussion en date du Jeu 16 Avr 2015 - 10:36

Grille mitterrand - Difficulté moyenne (rien de particulier, à part qu'il faut terminer sur huit)
Discussion en date du Dim 19 Avr 2015 - 9:33

Grille chirac - Particulier (dépourvue de pentagone et donc insusceptible de résolution classique)
Discussion en date du Dim 1 Mar 2015 - 17:29

Grille sarkozy - Difficulté moyenne
Discussion en date du Lun 20 Avr 2015 - 10:38

Grille hollande - Facile
Discussion en date du Mer 22 Avr 2015 - 9:22

Les sept jours de la semaine

Grille lundi - Facile
Discussion en date du Jeu 12 Mar 2015 - 9:51

Grille mardi - Difficulté moyenne (avec un exemple de cavexe qu'on peut dessiner mais non employer)
Discussion en date du Mar 14 Avr 2015 - 9:54

Grille mercredi - Difficulté moyenne
Discussion en date du Mer 8 Avr 2015 - 10:01

Grille jeudi - "Cinq ou huit" (intéressant: démontre l'utilité de la foi en la victoire)
Discussion en date du Ven 17 Avr 2015 - 10:42

Grille vendredi - Difficulté moyenne (difficile en raison de l'abondance des solutions)
Discussion en date du Mer 29 Avr 2015 - 9:52

Grille samedi - "Cinq ou huit"
Discussion en date du Lun 4 Mai 2015 - 8:58

Grille dimanche - "Cinq ou huit"
Discussion en date du Sam 9 Mai 2015 - 8:46

Allez, juste pour vous faire honte d'avoir peur de petits triangles de rien du tout, bande de surdoués à la noix:



Je vous signale qu'il y a des mômes que les jeujeux de triangles n'effraient pas: un petit tournoi de Triancey (bon, d'accord, pas la version "casse-tête") a été organisé tout récemment au collège de la Cerisaie de Charenton-le-Pont, et une douzaine de moutards très sages se sont creusé la tête pendant plus de deux heures avec mes grilles et mes pions bicolores, même que je crois bien qu'il s'est agi du premier tournoi de Triancey de l'histoire (allez, n'ayons pas peur des mots: de l'histoire de l'humanité).

Et vous, là, vous êtes pas foutus de me résoudre la moindre grille? Alors que vous vous dites surdoués? Mmm?

Bande de nases. Je m'en fous, je vais bouder, na.

Rha la vache, c'était vraiment hard-core mais j'ai réussi à trouver comment les résoudre intégralement en un minimum de coups. Je n'ai fais que le premier semestre, les autres solutions arriveront lorsque j'aurai le temps.

Ton exemple :
12 coups : 9 - 5 - 11 - 39 - 31 - 36 - 43 - 15 - 28 - 19 - 7 - 13

Janvier :

10 coups : 27 - 37 - 30 - 8 - 17 - 23 - 32 - 34 - 3 - 12

Février :

11 coups : 31 - 35 - 38 - 25 - 34 - 16 - 5 - 14 - 11 - 0 - 9

Mars :

11 Coups : 32 - 34 - 30 - 17 - 25 - 37 - 0 - 39 - 11 - 4 - 13

Avril :

10 coups : 29 - 35 - 26 - 2 - 32 - 16 - 18 - 12 - 9 - 14

Mai :

11 Coups : 34 - 36 - 23 - 16 - 18 - 21 - 2 - 13 - 31 - 9 - 39

Juin :

11 Coups : 35 - 36 - 32 - 25 - 28 - 21 - 10 - 23 - 16 - 2 - 14

Je pense qu'avec un peu d'efforts supplémentaires je peux même résoudre intégralement le jeu.

Bon allez, maintenant que j'y suis : la fin de l'année...

Juillet :

11 Coups : 17 - 41 - 36 - 6 - 9 - 31 - 0 - 33 - 38 - 22 - 24

Aout:

11 Coups : 33 - 40 - 35 - 25 - 27 - 23 - 13 - 17 - 9 - 4 - 11

Septembre :

12 Coups : 45 - 26 - 37 - 32 - 28 - 30 - 8 - 3 - 5 - 21 - 14 - 15

Octobre :

10 Coups : 20 - 25 - 17 - 0 - 10 - 24 - 36 - 22 - 5 - 32

Novembre :

11 Coups : 37 - 40 - 36 - 21 - 29 - 34 - 3 - 8 - 24 - 12 - 14

Decembre :

11 Coups : 37 - 39 - 27 - 20 - 22 - 12 - 8 - 14 - 32 - 4 - 34

hobb a écrit:Rha la vache, c'était vraiment hard-core mais j'ai réussi à trouver comment les résoudre intégralement en un minimum de coups.

Mais mais mais ma parole tu t'es cassé le tronc à tout renuméroter? Pourquoi diable?

Sans blague, ça sert à quoi que Petitagore il se décarcasse à programmer des interfaces clicables en Javascript?

Tes solutions m'ont l'air élégantes (très, même... enfin, je n'en ai encore étudié que deux), mais peux-tu être certain que tu as toujours trouvé le minimum minimorum, et que quelqu'un d'encore plus ingénieux que toi (ou un algorithme puissant) ne pourrait pas de temps à autre réussir à tout prendre avec encore un coup de moins que toi?

J'espère que tu peux faire mieux que me répondre "chiche"...

Oui, je suis certain que j'ai trouvé le minimum. Ce n'est pas par une méthode statistique, c'est déterministe. Au mieux on pourra les trouver plus rapidement (c'est meme sur, d'ailleurs je cherche encore à optimiser mon algo), mais c'est tout, il est impossible de les compléter en moins de coups. Par contre je pense qu'avec un peu de gymnastique je pourrai en faire une IA imbattable (ou match nul).

Quant à les numéroter, c'est nécessaire pour que mon algo puisse bouffer les paramètres d'entrée... peu importe la numération, mon algo sortira quand meme un minimum.

hobb a écrit:Oui, je suis certain que j'ai trouvé le minimum. Ce n'est pas par une méthode statistique, c'est déterministe.

Ah, tu as donc planché sur un algorithme, OK.

Pourrais-tu envisager d'en faire un logiciel libre? (oui, cette question est bassement intéressée) Et si la réponse est positive (autrement, je m'en fous   ), tu as écrit ça en quel langage?

Quant à les numéroter, c'est nécessaire pour que mon algo puisse bouffer les paramètres d'entrée... peu importe la numération, mon algo sortira quand meme un minimum.

Bien sûr. Mais tant qu'à faire, tu aurais pu prendre en paramètres d'entrée les fichiers XML exploités par mes listings Javascript, dans ce genre-là. C'est peut-être ce que tu as fait, d'ailleurs, mais alors je m'étonne que tu n'en aies pas profité pour récupérer la numérotation (balise "alias").

J'ai fais ça en fortran. Pour en faire un logiciel libre, why not, au pire je peux te passer les bibliothèques précompilées gratis sinon (parce que si ça a prit autant d'ampleur ça a peut etre moyen de finir en publi, auquel as il ne faut pas que je le mette en public avant qu'il ne parte en referee).

Non pour la numérotation je n'avais pas envie de m'emm****** à décrypter du xml avec du fortran (qui n'est quand meme pas super adapté pour bidouiller du texte tu en conviendras), donc en entrée je n'entre que les les 3 liens de chaque triangle avec les autres, il s'occupe du reste.

Et puis très honnetement, le code est vraiment compliqué (serieusement)... Je veux bien t'expliquer l'algorithme mais sur le net ça serait vraiment trop long...

Je viens de regarder, tu es sur de mettre le code à dispo de tout le monde ça ne risque pas de pourrir les jeux du meme type dispos sur le net ? C'est toi qui l'a inventé ?

Merci, je vais essayer de comprendre au moins la démarche générale.