Physique quantique for dummies
+32
Topsy Turvy
Opossum
Seskap
Mentounasc
câlin
Shadow Boxeur
doom
tim9.5
Stegos
siamois93
I am So Sure
LhaleeTreize
Iron D. Tramb
Ardel
AcideMatt
fift
jaravan
Le champ de l'abstraction
Ramen Taf'
i.a.
DLS
Tokamak
Like a Frog
REGBEL
prométhéus
ortolan
Darth Lord Tiger Kalthu
paela
bepo
Badak
Patate
Confiteor
36 participants
Page 7 sur 16
Page 7 sur 16 •  1 ... 6, 7, 8 ... 11 ... 16
1 ... 6, 7, 8 ... 11 ... 16 
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Jérémy34 a écrit:Je me demande ce que les observations et expériences quantiques ont de commun avec les relations humaines et les émotions...
Je crois que tu soulèves là la très grande méprise qui est à la source des patasciences diverses.
Il y a en effet dans la physique quantique une très grande tentation analogique avec des concepts philosophiques ou mieux encore avec une conception très poétique de la vie. C'est un peu comme si la mécanique quantique, l'extrême actuel du compréhensible de notre monde réel, rejoignait l'extrême sensitif de nos imaginaires. Deux appréhensions du monde extrêmement différentes qui se font écho malgré tout.
C'est intéressant mais aussi très dangereux que de se laisser aller à ces analogies sans garder en tête que les applications philosophiques, ou poétiques ne sont pas et ne seront jamais les mêmes que celles de la physique quantique. Toutes ont leur place, mais faut savoir trier ses lentilles.
Les émotions sont plutôt bien connues et comprises par la biochimie et la biophysique classique. Cela n'a pas grand chose de mystérieux qui aurait à voir avec les lois de la physique quantique.
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Moi j'y crois au "connais toi toi-même...".
Par exemple, j'imagine que si l'on ne comprenait/connaissait pas notre "déterminisme", nous n'etudirions plus les choses en relation avec (leur) l'environement.
Je crois aux lois qui bondissent, et je crois que nous sommes soumis à des lois qui bondissent.
Je crois que plus l'on a conaissance de soi, plus on a connaissance du monde.
Par exemple, j'imagine que si l'on ne comprenait/connaissait pas notre "déterminisme", nous n'etudirions plus les choses en relation avec (leur) l'environement.
Je crois aux lois qui bondissent, et je crois que nous sommes soumis à des lois qui bondissent.
Je crois que plus l'on a conaissance de soi, plus on a connaissance du monde.
Like a Frog- Messages : 1151
Date d'inscription : 24/05/2018
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Cuicui, Merci. Merci. Merci. Merci. Merci. ad libitum
Et c'est bien ce qui oppose un "clan" à un autre sur ce fil et sur TOUS les autres fils parlant de science (par exple neurologie, maths etc.)
Et c'est bien ce qui oppose un "clan" à un autre sur ce fil et sur TOUS les autres fils parlant de science (par exple neurologie, maths etc.)

Confiteor- Messages : 9164
Date d'inscription : 01/04/2017
Age : 65
Localisation : Drôme
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Sans les lois quantiques, tout s'effondrerait. C'est par ce prisme qu'on peut comprendre la photosynthèse, la lumière, la structure atomique des différents éléments du tableau périodique qui retrace toute la matière connue dans l'univers. Ou les étoiles à neutrons, l'aimantation, toutes sortes de phénomènes qui nous entourent et dont on en a même pas conscience.
Pour moi la physique (et la science en général) est source d'émerveillement pour mieux appréhender le réel, sachant aussi que c'est une construction humaine avec un côté mindfuck qui me plaît.
Pour moi la physique (et la science en général) est source d'émerveillement pour mieux appréhender le réel, sachant aussi que c'est une construction humaine avec un côté mindfuck qui me plaît.
- :

https://abstrusegoose.com/275
(Si jamais, ce fil développe la zone psi (une lettre grecque en forme de trident), au-dessus des oreilles du lapin. psi représente un état quantique qu'on a noté lpsi> ce qui me permet de faire la transition avec la suite de mon prochaine développement, sur f1(x,y), la lettre h barre et la lettre i, hihihhi !)
ce qui me permet de faire la transition avec la suite de mon prochaine développement, sur f1(x,y), la lettre h barre et la lettre i, hihihhi !)

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Confiteor a écrit:Cuicui, Merci. Merci. Merci. Merci. Merci. ad libitum
Et c'est bien ce qui oppose un "clan" à un autre sur ce fil et sur TOUS les autres fils parlant de science (par exple neurologie, maths etc.)
Entre monde fermé et monde ouvert ?
Like a Frog- Messages : 1151
Date d'inscription : 24/05/2018
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
L'exploration c'est de croire ou savoir qu'il existe autre chose.
Like a Frog- Messages : 1151
Date d'inscription : 24/05/2018
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Les propos délibérément elliptiques, hermétiques et sentencieux sont très avantageux.
Ils permettent d'avoir toujours raison et d'afficher un sentiment de supériorité implicite sur autrui sans risquer les foudres de la modération.
Éventuellement, ils sont totalement vides de sens et alors revendiquent une forme tacite de poésie lorsqu'on le fait remarquer.
Et alors le débat est clos d'autorité puisque ...
Certains en font une spécialité et parsèment de leurs perles (?) tous les fils auxquels ils participent.
Une forme de pollution mentale comme une autre.
Un bon chasseur sachant chasser sait se chasser lui-même lorsque le besoin se fait sentir.
Ils permettent d'avoir toujours raison et d'afficher un sentiment de supériorité implicite sur autrui sans risquer les foudres de la modération.
Éventuellement, ils sont totalement vides de sens et alors revendiquent une forme tacite de poésie lorsqu'on le fait remarquer.
Et alors le débat est clos d'autorité puisque ...
Certains en font une spécialité et parsèment de leurs perles (?) tous les fils auxquels ils participent.
Une forme de pollution mentale comme une autre.
Un bon chasseur sachant chasser sait se chasser lui-même lorsque le besoin se fait sentir.

Confiteor- Messages : 9164
Date d'inscription : 01/04/2017
Age : 65
Localisation : Drôme
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Ça vient comme ça.
Dsl si ça embete ou si ça sonne "délibéré" je sais pas quoi.
Et je ne vois pas le rapport avec la modération.
Dsl si ça embete ou si ça sonne "délibéré" je sais pas quoi.
Et je ne vois pas le rapport avec la modération.
Like a Frog- Messages : 1151
Date d'inscription : 24/05/2018
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
- Spoiler:
Ouaich ! Moi je n'ai jamais autant écrit de poèmes que quand j'étudiais la biochimie des plantes médicinales.
Pour moi la physique (et la science en général) est source d'émerveillement pour mieux appréhender le réel...
Mais c'est aussi une source sans fin pour faire des voyages dans l'imaginaire.
Je me suis fait avoir un jour par un scientifique qui m'a fourgué du tacchyon dans ses théories et je suis tombée amoureuse de cette tite chose invisible pour la science mais pas pour mon imagination. Imaginez une particule qui défie la vitesse de la lumière ! Qu'est-ce que j'ai aimé ! Dr Who à coté, c'était un rigolo.
Jusqu'à ce que j'apprenne qu'on n'avait pas prouvé son existence. Qu'est-ce que j'ai été déçue !
J'avais posé sur ce forum dans le rayon "rationnel" un article d'un physicien qui permettait de refourguer aux oubliettes tout ce qui relève de la patascience médicale qu'on voit parfois à propos de la médecine quantique.Un bon chasseur sachant chasser sait se chasser lui-même lorsque le besoin se fait sentir.
Faut-il te répondre les chaussettes de l'archiduchesse ?
Plus sérieusement : ici, comme ailleurs, je regarde assez interloquée ces guerres de "clans", rationnel/irrationnel, savoirs/croyances.
Lire toutes sortes de foutaises patascientifiques ou au contraire lire un mépris de ce qui est du genre "croyance" me désole toujours autant.
Je ne comprends pas que les nouvelles "rationalités" à la mode des zététiques condamnent avec tant de force tout ce qui relève de la croyance. On sait bien que notre cerveau a tout autant besoin de "croire" que de "savoir". Il me semble qu'il suffirait de dénoncer les croyances qui servent à asservir des individus au profit d'autres et la démarche zététique a tous les outils pour le faire. Mais cela me parait abusif de dénoncer tout ce qui relève de la croyance sous seul prétexte que c'est du registre de la croyance. Croire et savoir sont deux potentialités de notre mental, pourquoi devrions-nous en perdre un au profit d'un autre ? La part imaginaire de notre psychisme est aussi source d'accès à la recherche selon des modalités qui peuvent être "scientifique".
Pour moi, la Raison est cette part de nous qui sait distinguer ce que nous savons, ce que nous croyons, ce que nous imaginons. Ce sont plusieurs modalités qui nous permettent d'entrer en relation tant avec les autres qu'avec notre environnement. Certes les frontières sont parfois floues et ouvrent à toutes les foutaises dangereuses mais on a quantité d'outils pour savoir nous en protéger, en tant qu'individus comme en tant que groupe social ou sociétal.
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Résumé sur le spin
J'ai enfin trouvé une vidéo qui explique le concept du spin (10 min) et la toupie tippe-top.
Tout à gauche, on reconnaît notre stern-gerlach, avec la partie "NOTRE MONDE". Et en-dessous, le "MONDE QUANTIQUE" qui est notre espace de Hilbert. Puis un VECTEUR D'ESPACE qui n'est rien d'autre qu'un spinneur.
On y trouve aussi les symboles l+> et UP.
Enfin, tout à droite, le fameux h = 6,626 070 040 fois 10 puissance moins trente-quatre qui est le plus petit saut d'énergie possible dans l'univers. C'est-à-dire 0,000000000000000000000000000000006 Joules seconde (est-ce qu'on met s à Joule dans ce cas?). Si on change l'unité, on obtient, 4,135 667 662 × 10−15 eV s. (seulement 0, 14 zéros après la virgule).
Les physiciens ont quand même réussi à planquer la constante 2fois pi sous la constante de Planck h (qui est le premier à l'avoir utilisé). On obtient alors h barre = ħ = h / 2 π ≈ 1,054 571 800 × 10−34 J s. On remarque qu'on est toujours à 10-34. L'ordre de grandeur ne change pas.
Ainsi, l'électron peut être dans un état spin down d'énergie -1/2ħ, et passer à l'état +1/2ħ en absorbant le minimum d'énergie possible dans la nature, à savoir ħ.
A partir de la 10ème minute, Jean-Claude Audet montre bien la difficulté à conceptualiser le monde nanoscopique : électron, spin.
J'ai enfin trouvé une vidéo qui explique le concept du spin (10 min) et la toupie tippe-top.
Tout à gauche, on reconnaît notre stern-gerlach, avec la partie "NOTRE MONDE". Et en-dessous, le "MONDE QUANTIQUE" qui est notre espace de Hilbert. Puis un VECTEUR D'ESPACE qui n'est rien d'autre qu'un spinneur.
On y trouve aussi les symboles l+> et UP.
Enfin, tout à droite, le fameux h = 6,626 070 040 fois 10 puissance moins trente-quatre qui est le plus petit saut d'énergie possible dans l'univers. C'est-à-dire 0,000000000000000000000000000000006 Joules seconde (est-ce qu'on met s à Joule dans ce cas?). Si on change l'unité, on obtient, 4,135 667 662 × 10−15 eV s. (seulement 0, 14 zéros après la virgule).
Les physiciens ont quand même réussi à planquer la constante 2fois pi sous la constante de Planck h (qui est le premier à l'avoir utilisé). On obtient alors h barre = ħ = h / 2 π ≈ 1,054 571 800 × 10−34 J s. On remarque qu'on est toujours à 10-34. L'ordre de grandeur ne change pas.
Ainsi, l'électron peut être dans un état spin down d'énergie -1/2ħ, et passer à l'état +1/2ħ en absorbant le minimum d'énergie possible dans la nature, à savoir ħ.
A partir de la 10ème minute, Jean-Claude Audet montre bien la difficulté à conceptualiser le monde nanoscopique : électron, spin.
Dernière édition par tim9.5 le Mer 13 Juin 2018 - 16:16, édité 2 fois

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
E1. Les nombres complexes : approche algébrique
Je vous propose une ballade dans les nombres imaginaires, qui font partie du minimum à connaître avant d'entamer la physique quantique. Sans eux, point de mathématique quantique !
Petit rappel sur les nombres.
Premièrement on connaît :
a) les nombres entiers pour compter des objets un à un;
b) le zéro, très pratique;
c) les nombres négatifs pour compter aussi nos dettes;
d) des nombres décimaux pour partager l'argent en morceaux (4,99 €);
e) des nombres fractionnaires qui sont une combinaison de deux nombres entiers, en vue d'un partage d'héritage ou de gâteaux.
f) Ces nombres peuvent s'écrirent aussi sous forme de pourcentage, très utile en probabilité
g) des symboles pour des nombres impossibles à écrire, car sans périodicité, comme le nombre pi.
D'autres symboles tel racine de 16 = 4 sont aussi de la partie.
On a cerné ainsi tous les nombres réels.
Deuxièmement l'école introduit les lettres dans les calculs d'adolescents. L'inconnue x ou y.
L'élève doit alors s'habituer à donner des réponses qui ne sont plus écrites de manières compactes.
Auparavant il y avait 12 vaches comme unique solution. Maintenant la bonne réponse prend la forme 5x + 2. Pas 7x ni 7, mais 5x + 2. Le calcul devient littéral.
Nouvelles règles du jeu :
1) x + x = 2x (règle de l'addition)
2) x fois x = x au carré (une multiplication)
3) a(b + c) = ab + ac (la distributivité).
4) (a + b)(c + d) = ac + ad + bc + bd (la double distributivité).
Avec des raccourcis bien connus : (a + b)(a - b) = a "au carré" - b "au carré".
Nouveau symbole, la lettre i
i comme imaginaire. La seule propriété qu'on exige de lui est que lorsqu'on le multiplie à lui-même, on obtient -1.
Voici notre nouvelle famille de nombres :

Un nombre complexe z peut alors s'écrire sous la forme a + bi. Exemple, 4 = 4 +0i; 12 + 3i, etc.
Quelques calculs :
si z = a + bi et w = c + di, pour n'importe quel nombre réel a,b, c et d, alors
a) z+w = a + bi + c + di (on remplace z et w) = a+b + (b+d)i (on met de l'ordre).
b) z fois w = zw = (a + bi)(c+di) = ac + adi + bci + bdii (la double distributivité). Mais bdii = bd fois (-1) = -bd. Donc zw devient ac + adi + bci - bd. On remet de l'ordre pour obtenir zw = ac-bd + (ad-bc)i.
Bref, si tu te rappelles comment manipuler les x, utiliser le nombre i ne pose aucun problème.
hihihi devient -h au cube i, mais c'est moins drôle.
Je vous propose une ballade dans les nombres imaginaires, qui font partie du minimum à connaître avant d'entamer la physique quantique. Sans eux, point de mathématique quantique !
Petit rappel sur les nombres.
Premièrement on connaît :
a) les nombres entiers pour compter des objets un à un;
b) le zéro, très pratique;
c) les nombres négatifs pour compter aussi nos dettes;
d) des nombres décimaux pour partager l'argent en morceaux (4,99 €);
e) des nombres fractionnaires qui sont une combinaison de deux nombres entiers, en vue d'un partage d'héritage ou de gâteaux.
f) Ces nombres peuvent s'écrirent aussi sous forme de pourcentage, très utile en probabilité
g) des symboles pour des nombres impossibles à écrire, car sans périodicité, comme le nombre pi.
D'autres symboles tel racine de 16 = 4 sont aussi de la partie.
On a cerné ainsi tous les nombres réels.
Deuxièmement l'école introduit les lettres dans les calculs d'adolescents. L'inconnue x ou y.
L'élève doit alors s'habituer à donner des réponses qui ne sont plus écrites de manières compactes.
Auparavant il y avait 12 vaches comme unique solution. Maintenant la bonne réponse prend la forme 5x + 2. Pas 7x ni 7, mais 5x + 2. Le calcul devient littéral.
Nouvelles règles du jeu :
1) x + x = 2x (règle de l'addition)
2) x fois x = x au carré (une multiplication)
3) a(b + c) = ab + ac (la distributivité).
4) (a + b)(c + d) = ac + ad + bc + bd (la double distributivité).
Avec des raccourcis bien connus : (a + b)(a - b) = a "au carré" - b "au carré".
Nouveau symbole, la lettre i
i comme imaginaire. La seule propriété qu'on exige de lui est que lorsqu'on le multiplie à lui-même, on obtient -1.
Voici notre nouvelle famille de nombres :

Un nombre complexe z peut alors s'écrire sous la forme a + bi. Exemple, 4 = 4 +0i; 12 + 3i, etc.
Quelques calculs :
si z = a + bi et w = c + di, pour n'importe quel nombre réel a,b, c et d, alors
a) z+w = a + bi + c + di (on remplace z et w) = a+b + (b+d)i (on met de l'ordre).
b) z fois w = zw = (a + bi)(c+di) = ac + adi + bci + bdii (la double distributivité). Mais bdii = bd fois (-1) = -bd. Donc zw devient ac + adi + bci - bd. On remet de l'ordre pour obtenir zw = ac-bd + (ad-bc)i.
Bref, si tu te rappelles comment manipuler les x, utiliser le nombre i ne pose aucun problème.
- Une vidéo pour t'entraîner (10 min):
hihihi devient -h au cube i, mais c'est moins drôle.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
F. Les postulats de la mécanique quantique
Voici l'ultime but de ce fil :

Avec une petite citation trouvée sur le site de l'image ci-desssus :
"So an angel can be in one place in one instant and in another in the next instant, without any time intervening. And he will be partly in one place and partly in another, not as though his substance were divisible into parts; but simply because his power will be applying itself, at any given moment, in part to one place and in part to the place next to it." (Thomas Aquinas) La mécanique quantique a un côté angélique.
Voici le cadre de notre exploration de la physique, qui correspond au rectangle saumon:
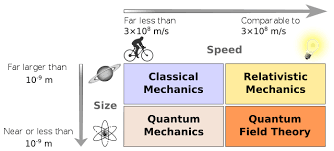
Le Larousse nous dit qu'un postulat est "une proposition que l'on demande d'admettre avant un raisonnement, que l'on ne peut démontrer et qui ne saurait être mis en doute." Shut up and calculate, en négatif. Ces postulats servent à décrire un système physique isolé, c'est-à-dire qui n'agit pas hors de lui. Par exemple le spin de l'électron est influencé par un gros aimant, mais le spin au contraire n'influence pas le gros aimant, ni les atomes autour de lui par exemple.

Résumé des postulats
Comme la formulation des postulats varie selon les auteurs, je vais prendre ceux énoncés par Fabien Bosnard, dans son cours Introduction à la mécanique quantique, téléchargeable en pdf (p.34-40).
Postulat 1 A tout système physique correspond un espace de Hilbert, appelé l'espace des états.
"Par ce postulat, nous déclarons que tout système physique est soumis aux lois quantiques. (...) Dans la limite où un système devient macroscopique, les lois quantiques se réduisent aux lois de la mécanique classique. Cette croyance est justifiée rigoureusement dans de nombreux cas." (Bosnard). Il y a toutefois deux domaines à explorer :
1) lors de l'interaction entre un système microscopique et macroscopique (entre le spin de l'électron et l'appareil de Stern-Gerlach);
2) lorsque la gravitation entre en jeu, car cette force possède une portée dans tout l'univers, "ce qui fait qu'en principe tout système est soumis à cette force !". Dans les cas microscopiques toutefois, elle est négligeable. Le grand rêve des physiciens, unir les mécaniques quantiques et relativistes (le rectangle saumon et jaune ci-dessus) en passant par la théorie quantique des champs (rectangle orange), notamment celle développée par Carlo Rovelli.
Une autre formulation du postulat 1 : principe de superposition
L'état d'un système est entièrement défini, à chaque instant t, par un vecteur lψ(t)> d'un espace de Hilbert.
Le vecteur lψ(t)>, c'est celui qui est tout à gauche sur l'image de Koussour.
Exemple d'Espace de Hilbert à deux dimensions
On peut représenter un vecteur par deux nombres entre parenthèses, séparés par une virgule comme ci-dessous :

a) addition de vecteurs
Nommons le premier vecteur lp>=(2,1), et le deuxièmej lq>=(1,2).
Astuce de dummie : on utilise désormais une grosse calculette nommée https://www.wolframalpha.com
Pour qu'elle fonctionne, on utilise {} ou lieu de ().
Dessinons lp> que l'on écrit vector {2,1} dans wolfram : https://www.wolframalpha.com/input/?i=vector+%7B2,1%7D
Pour simplifier, on écrira lp>={2,1} qui est un point. Mais il suffit d'imaginer la flèche qui parte de (0,0) et qui pointe sur ce point pour obtenir notre vecteur.
Petits calculs :
a) lp> + lq> = {2,1}+{1,2} = {3,3}.
b) on fait de même avec des nombres complexes. Si lp> = {2+i,1} et lq> = {5,3-i}, alors lp>+lq> = {2+i+5,1+3-i} ={7+i,4-i}. Bravo !
b) multiplication d'un nombre par un vecteur (pour l'allonger par exemple)
1) si lp>={2,1}, alors 5lp>={5 fois 2,5 fois1}={10,5}. Dans wolfram, écrire 5{2,1}
2) (4+3i)lp> = (4+3i){2,1} = {(4+3i) fois 2, (4+3i) fois 1} ("distributivité") = {8+6i, 4+3i} (distributivité)
b) multiplication de deux vecteurs lp> et lq>
En fait ça ne marche pas, car il y a une subtilité à cause des nombres complexes... Mais tu vas puiser dans tes dernières ressources intellectuelles pour la surmonter, sinon revient demain.
Astuce 1: a-bi est le conjugué du nombre complexe a+bi. Exemple : 4-5i est le conjugué de 4+5i. On ne change que le signe du nombre qui est collé au i. De même, a+6i est le conjugué de a-6i.
Astuce 2 : on note <pl le vecteur conjugué du vecteur lp>.
Exemples :
1) Si lp>={2,1}, alors son conjugué est <pl={2,1} car il n'y a pas de partie imaginaire.
2) Si lp>={2+i,1} alors <pl={2-i,1}
3) Pour lq>={-2-i,1+6i} on obtient <ql= {-2+i,1-6i}
Finalement, la multiplication des vecteur lp> et lq> s'écrit <plq> = <pl fois lq> = {a,b}{a',b'} = aa' + bb'
Exemples plus parlant :
1) Si lp>={2,3} donc <pl={2,3}. Pour lq>={5,6}, alors <plq> = {2,3}{5,6} = 2 fois 5 + 3 fois 6 = 10 + 18 (on fait d'abord les multiplications avant les additions) = 28.
2) Pour lp>={2,3+i}, alors <pl={2,3 moins i} et <plq> = {2,3 - i}{5,6}= 2 fois 5 + (3-i) fois 6 = 10 + 18-6i (distributivité) = 28-6i
3) lp>={2-5i,3+i} et lq>={5+4i,3+i} donne <plq>={2 plus 5i,3 moins i}{5+4i,3+i} = (2 + 5i)(5+4i) + (3-i)(3+i) = (10+8i+25i-20) (double distributivité) + (9+3i-3i+1) (double distributivité avec i fois i = -1) = (30+33i) + 10 = 40 + 33i.
Conclusion : voici enfin un espace de Hilbert décrit explicitement. Au niveau du calcul, cela ne nécessite que de connaître des notions vues à l'école obligatoire : vecteurs, calcul littéral simple, priorité des opérations, double distributivité. On rajoute i au carré = -1.
Voici l'ultime but de ce fil :

Avec une petite citation trouvée sur le site de l'image ci-desssus :
"So an angel can be in one place in one instant and in another in the next instant, without any time intervening. And he will be partly in one place and partly in another, not as though his substance were divisible into parts; but simply because his power will be applying itself, at any given moment, in part to one place and in part to the place next to it." (Thomas Aquinas) La mécanique quantique a un côté angélique.
Voici le cadre de notre exploration de la physique, qui correspond au rectangle saumon:
Le Larousse nous dit qu'un postulat est "une proposition que l'on demande d'admettre avant un raisonnement, que l'on ne peut démontrer et qui ne saurait être mis en doute." Shut up and calculate, en négatif. Ces postulats servent à décrire un système physique isolé, c'est-à-dire qui n'agit pas hors de lui. Par exemple le spin de l'électron est influencé par un gros aimant, mais le spin au contraire n'influence pas le gros aimant, ni les atomes autour de lui par exemple.

Résumé des postulats
Comme la formulation des postulats varie selon les auteurs, je vais prendre ceux énoncés par Fabien Bosnard, dans son cours Introduction à la mécanique quantique, téléchargeable en pdf (p.34-40).
Postulat 1 A tout système physique correspond un espace de Hilbert, appelé l'espace des états.
"Par ce postulat, nous déclarons que tout système physique est soumis aux lois quantiques. (...) Dans la limite où un système devient macroscopique, les lois quantiques se réduisent aux lois de la mécanique classique. Cette croyance est justifiée rigoureusement dans de nombreux cas." (Bosnard). Il y a toutefois deux domaines à explorer :
1) lors de l'interaction entre un système microscopique et macroscopique (entre le spin de l'électron et l'appareil de Stern-Gerlach);
2) lorsque la gravitation entre en jeu, car cette force possède une portée dans tout l'univers, "ce qui fait qu'en principe tout système est soumis à cette force !". Dans les cas microscopiques toutefois, elle est négligeable. Le grand rêve des physiciens, unir les mécaniques quantiques et relativistes (le rectangle saumon et jaune ci-dessus) en passant par la théorie quantique des champs (rectangle orange), notamment celle développée par Carlo Rovelli.
Une autre formulation du postulat 1 : principe de superposition
L'état d'un système est entièrement défini, à chaque instant t, par un vecteur lψ(t)> d'un espace de Hilbert.
Le vecteur lψ(t)>, c'est celui qui est tout à gauche sur l'image de Koussour.
Exemple d'Espace de Hilbert à deux dimensions
On peut représenter un vecteur par deux nombres entre parenthèses, séparés par une virgule comme ci-dessous :

a) addition de vecteurs
Nommons le premier vecteur lp>=(2,1), et le deuxièmej lq>=(1,2).
Astuce de dummie : on utilise désormais une grosse calculette nommée https://www.wolframalpha.com
Pour qu'elle fonctionne, on utilise {} ou lieu de ().
Dessinons lp> que l'on écrit vector {2,1} dans wolfram : https://www.wolframalpha.com/input/?i=vector+%7B2,1%7D
Pour simplifier, on écrira lp>={2,1} qui est un point. Mais il suffit d'imaginer la flèche qui parte de (0,0) et qui pointe sur ce point pour obtenir notre vecteur.
Petits calculs :
a) lp> + lq> = {2,1}+{1,2} = {3,3}.
b) on fait de même avec des nombres complexes. Si lp> = {2+i,1} et lq> = {5,3-i}, alors lp>+lq> = {2+i+5,1+3-i} ={7+i,4-i}. Bravo !
b) multiplication d'un nombre par un vecteur (pour l'allonger par exemple)
1) si lp>={2,1}, alors 5lp>={5 fois 2,5 fois1}={10,5}. Dans wolfram, écrire 5{2,1}
2) (4+3i)lp> = (4+3i){2,1} = {(4+3i) fois 2, (4+3i) fois 1} ("distributivité") = {8+6i, 4+3i} (distributivité)
b) multiplication de deux vecteurs lp> et lq>
En fait ça ne marche pas, car il y a une subtilité à cause des nombres complexes... Mais tu vas puiser dans tes dernières ressources intellectuelles pour la surmonter, sinon revient demain.
Astuce 1: a-bi est le conjugué du nombre complexe a+bi. Exemple : 4-5i est le conjugué de 4+5i. On ne change que le signe du nombre qui est collé au i. De même, a+6i est le conjugué de a-6i.
Astuce 2 : on note <pl le vecteur conjugué du vecteur lp>.
Exemples :
1) Si lp>={2,1}, alors son conjugué est <pl={2,1} car il n'y a pas de partie imaginaire.
2) Si lp>={2+i,1} alors <pl={2-i,1}
3) Pour lq>={-2-i,1+6i} on obtient <ql= {-2+i,1-6i}
Finalement, la multiplication des vecteur lp> et lq> s'écrit <plq> = <pl fois lq> = {a,b}{a',b'} = aa' + bb'
Exemples plus parlant :
1) Si lp>={2,3} donc <pl={2,3}. Pour lq>={5,6}, alors <plq> = {2,3}{5,6} = 2 fois 5 + 3 fois 6 = 10 + 18 (on fait d'abord les multiplications avant les additions) = 28.
2) Pour lp>={2,3+i}, alors <pl={2,3 moins i} et <plq> = {2,3 - i}{5,6}= 2 fois 5 + (3-i) fois 6 = 10 + 18-6i (distributivité) = 28-6i
3) lp>={2-5i,3+i} et lq>={5+4i,3+i} donne <plq>={2 plus 5i,3 moins i}{5+4i,3+i} = (2 + 5i)(5+4i) + (3-i)(3+i) = (10+8i+25i-20) (double distributivité) + (9+3i-3i+1) (double distributivité avec i fois i = -1) = (30+33i) + 10 = 40 + 33i.
Conclusion : voici enfin un espace de Hilbert décrit explicitement. Au niveau du calcul, cela ne nécessite que de connaître des notions vues à l'école obligatoire : vecteurs, calcul littéral simple, priorité des opérations, double distributivité. On rajoute i au carré = -1.
Dernière édition par tim9.5 le Sam 16 Juin 2018 - 13:10, édité 3 fois

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Bravo, bravo et merci !

Confiteor- Messages : 9164
Date d'inscription : 01/04/2017
Age : 65
Localisation : Drôme
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
F2. Deuxième postulat de la mécanique quantique
"A chaque instant t, l'état d'un système physique est décrit par un vecteur non nul lψ(t)> (psi de té) de l'espace des états, appelé vecteur d'état. Deux vecteurs non nuls représentent le même état si, et seulement si, ils sont proportionnels." (p.34) (On peut donc les remplacer en toute rigueur par des droites décrites par des nombres complexes.)
Remarque de Bosnard : ce postulat "fait référence au temps comme si ce dernier était un paramètre extérieur à tout système physique et indépendant de l'observateur. Or nous savons qu'il n'en n'est rien : la théorie de la relativité restreinte, validée par de nombreuses expériences, a démontré que la variable de temps n'a pas de sens physique intrinsèque, et que sa définition dépend du mouvement relatif de l'observateur et du système physique considéré."
De fait la mécanique quantique n'est pas compatible avec des objets de très grandes vitesses.
Ces deux postulats "introduisent une caractéristique de la mécanique quantique qui n'a pas d'équivalent classique : (...) le principe de superposition quantique.
Si lψ(t)> et lφ(t)> sont deux vecteurs d'états d'un système physique, alors alψ(t)> + blφ(t)> est aussi un vecteur d'état du système. Tout ceci n'a de sens que "si l'on sait interpréter les vecteurs d'états. Comment peut-on les utiliser concrètement? C'est l'objet des deux postulats suivants.
Exemple de superposition : pour l+> = {0,1} et l-> ={1,0} alors
lp> = 3 fois l+> + (1-i) fois l->
= 3 fois {0,1} + (1-i) fois {1,0}
= 3.{0,1} +(1-i).{1,0}
= {0,3} +{(1-i),0}
= {(1-i),3}
est aussi un vecteur d'état du système.
A contrario, tout vecteur de dimension 2 peut s'écrire comme combinaison linéaire de l+> et l->, par projection.
La projection sur l+> du vecteur lp> vaut <+lp>, c'est-à-dire le conjugué du vecteur l+> fois le vecteur lp>..

Considérons deux vecteurs la> et lb> de longueur 1 pour simplifier. On projette lb> sur la>, à angle droit. Ce vecteur bleu est alors égal au vecteur la> multiplié par le nombre <alb>, qui n'est rien d'autre que la multiplication entre le vecteur conjugué <al et le vecteur lb>.
Le vecteur bleu s'écrit alors <alb>fois la> = <alb>la>
En effet, pour lp>= {(1-i),3}, alors
<+lp> = {le conjugué de l+>} fois lp>
= {0,1 (on change les signes des i invisibles!) } fois {(1-i),3}
= 0 fois (1-i) plus 1 fois 3
= 0 + 3 (les fois d'abord !)
= 3.
Ainsi le vecteur lp>= {(1-i),3} = 3l+> + un nombre complexe fois l->.
Ce nombre complexe vaut
<-lp> = {le conjugué de l->} fois lp>
= {1,0}.{(1-i),3}
= 1 fois (1-i) + 0 fois 3}
= 1-i + 0
= 1-i.
Donc lp> = {(1-i),3} s'écrit aussi lp> = 3l+> + (1-i)l->. Tu suis toujours ? Yes !
Avec Wolframalpha :
avec l+> = {0,1} , l-> ={1,0} et lp>= {(1-i),3}
on écrit <+lp> ainsi conjugate[{0,1}].{(1-i),3}, ce qui donne 3.
et <-lp> devient conjugate[{1,0}].{(1-i),3}, qui vaut 1-i.
En résumé lp> = <+lp> fois l+> plus <-lp> fois l->.

avec a = <A+lψ>.
Remarque : ceci reprend plus formellement la section B.3 sur la multiplication des vecteurs, et B.4 sur les projections, page 10 de ce fil.
"A chaque instant t, l'état d'un système physique est décrit par un vecteur non nul lψ(t)> (psi de té) de l'espace des états, appelé vecteur d'état. Deux vecteurs non nuls représentent le même état si, et seulement si, ils sont proportionnels." (p.34) (On peut donc les remplacer en toute rigueur par des droites décrites par des nombres complexes.)
Remarque de Bosnard : ce postulat "fait référence au temps comme si ce dernier était un paramètre extérieur à tout système physique et indépendant de l'observateur. Or nous savons qu'il n'en n'est rien : la théorie de la relativité restreinte, validée par de nombreuses expériences, a démontré que la variable de temps n'a pas de sens physique intrinsèque, et que sa définition dépend du mouvement relatif de l'observateur et du système physique considéré."
De fait la mécanique quantique n'est pas compatible avec des objets de très grandes vitesses.
Ces deux postulats "introduisent une caractéristique de la mécanique quantique qui n'a pas d'équivalent classique : (...) le principe de superposition quantique.
Si lψ(t)> et lφ(t)> sont deux vecteurs d'états d'un système physique, alors alψ(t)> + blφ(t)> est aussi un vecteur d'état du système. Tout ceci n'a de sens que "si l'on sait interpréter les vecteurs d'états. Comment peut-on les utiliser concrètement? C'est l'objet des deux postulats suivants.
Exemple de superposition : pour l+> = {0,1} et l-> ={1,0} alors
lp> = 3 fois l+> + (1-i) fois l->
= 3 fois {0,1} + (1-i) fois {1,0}
= 3.{0,1} +(1-i).{1,0}
= {0,3} +{(1-i),0}
= {(1-i),3}
est aussi un vecteur d'état du système.
A contrario, tout vecteur de dimension 2 peut s'écrire comme combinaison linéaire de l+> et l->, par projection.
La projection sur l+> du vecteur lp> vaut <+lp>, c'est-à-dire le conjugué du vecteur l+> fois le vecteur lp>..

Considérons deux vecteurs la> et lb> de longueur 1 pour simplifier. On projette lb> sur la>, à angle droit. Ce vecteur bleu est alors égal au vecteur la> multiplié par le nombre <alb>, qui n'est rien d'autre que la multiplication entre le vecteur conjugué <al et le vecteur lb>.
Le vecteur bleu s'écrit alors <alb>fois la> = <alb>la>
En effet, pour lp>= {(1-i),3}, alors
<+lp> = {le conjugué de l+>} fois lp>
= {0,1 (on change les signes des i invisibles!) } fois {(1-i),3}
= 0 fois (1-i) plus 1 fois 3
= 0 + 3 (les fois d'abord !)
= 3.
Ainsi le vecteur lp>= {(1-i),3} = 3l+> + un nombre complexe fois l->.
Ce nombre complexe vaut
<-lp> = {le conjugué de l->} fois lp>
= {1,0}.{(1-i),3}
= 1 fois (1-i) + 0 fois 3}
= 1-i + 0
= 1-i.
Donc lp> = {(1-i),3} s'écrit aussi lp> = 3l+> + (1-i)l->. Tu suis toujours ? Yes !
Avec Wolframalpha :
avec l+> = {0,1} , l-> ={1,0} et lp>= {(1-i),3}
on écrit <+lp> ainsi conjugate[{0,1}].{(1-i),3}, ce qui donne 3.
et <-lp> devient conjugate[{1,0}].{(1-i),3}, qui vaut 1-i.
En résumé lp> = <+lp> fois l+> plus <-lp> fois l->.

avec a = <A+lψ>.
Remarque : ceci reprend plus formellement la section B.3 sur la multiplication des vecteurs, et B.4 sur les projections, page 10 de ce fil.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
merci tim9.5 ; pour d'autres je note l'importance de la plupart de leurs représentations à considérer la physique quantique comme non connectée à l'humain, cette absence de connexion est un non-sens dans mes représentations puisque ce sont des humains qui étudient l'univers dans lequel ils évoluent, dans le même espace-temps que l'univers lui-même.
cette représentation de considérer les êtres non liés entre eux et non liés à l'univers lui-même provoque de nombreuses souffrances auxquelles je me refuse de contribuer.
je préfère étudier la nature des liens.
cette représentation de considérer les êtres non liés entre eux et non liés à l'univers lui-même provoque de nombreuses souffrances auxquelles je me refuse de contribuer.
je préfère étudier la nature des liens.
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Ettore Majorana, le « physicien absolu », un génie avant-gardiste dont les travaux sont à présent étudiés et pris en considération dans quantité de publications en Physique théorique.

Tokamak- Messages : 3004
Date d'inscription : 24/05/2017
Localisation : Wonderland
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Esquisse de réponse pour Jérémy d'un des meilleurs philosophe de la mécanique quantique:
en version pdf : https://duckduckgo.com/?q=physique+quantique+et+r%C3%A9alit%C3%A9+bernard+d%27Espagnat+pdf&t=ffab&ia=videos
En effet, la physique quantique ressemble à son formalisme à la physique classique, mais elle ouvre sur une réalité qui ne peut plus être celle d'"avant" avec des corps qui se meuvent et des ondes lumineuses, sans lien avec l'observateur. Justement la mécanique quantique amène sur le fait que "beaucoup font valoir que nous faisons nous-même partie du monde, que nous sommes "dedans", et qu'aussi longtemps qu'on est dans quelque chose il est impossible de se former une vue exacte - une God's eye view, comme disent les Anglo-Saxons- de ce quelque chose." (p.5)
Il prend alors l'exemple de l'arc-en-ciel, pour pasticher ainsi : "la mécanique quantique et l'apparence d'un monde classique."
Il conclut provisoirement : "Pour toutes ces raisons, je tiendrai donc, à partir d'ici, pour acquis que les informations fournies par la physique actuelle ne sont pas des descriptions d'une réalité qui serait extérieure à tout observateur." (p.6)
Ensuite il développe deux points de vue sur le mot "réalisme" qui tient compte des découvertes de la mécanique quantique.
De plus il rejette la conception "communément reçue, d'un réel-en-soi atomisé en une multitude d'éléments simples, quarks, électrons, etc... plus ou moins localisés, qui par combinaisons engendreraient des objets et êtres composant le monde - cette vision-là est intenable à l'heure actuelle, nous l'avons vu -, mais au contraire celle d'un réel essentiellement global - quelque chose comme l'UN de Plotin- mais que nos esprits ne perçoivent que sous les apparences d'une multitude d'objets."
Et sa conclusion finale et magnifique au soir de sa vie. Je te laisse la découvrir.
en version pdf : https://duckduckgo.com/?q=physique+quantique+et+r%C3%A9alit%C3%A9+bernard+d%27Espagnat+pdf&t=ffab&ia=videos
En effet, la physique quantique ressemble à son formalisme à la physique classique, mais elle ouvre sur une réalité qui ne peut plus être celle d'"avant" avec des corps qui se meuvent et des ondes lumineuses, sans lien avec l'observateur. Justement la mécanique quantique amène sur le fait que "beaucoup font valoir que nous faisons nous-même partie du monde, que nous sommes "dedans", et qu'aussi longtemps qu'on est dans quelque chose il est impossible de se former une vue exacte - une God's eye view, comme disent les Anglo-Saxons- de ce quelque chose." (p.5)
Il prend alors l'exemple de l'arc-en-ciel, pour pasticher ainsi : "la mécanique quantique et l'apparence d'un monde classique."
Il conclut provisoirement : "Pour toutes ces raisons, je tiendrai donc, à partir d'ici, pour acquis que les informations fournies par la physique actuelle ne sont pas des descriptions d'une réalité qui serait extérieure à tout observateur." (p.6)
Ensuite il développe deux points de vue sur le mot "réalisme" qui tient compte des découvertes de la mécanique quantique.
De plus il rejette la conception "communément reçue, d'un réel-en-soi atomisé en une multitude d'éléments simples, quarks, électrons, etc... plus ou moins localisés, qui par combinaisons engendreraient des objets et êtres composant le monde - cette vision-là est intenable à l'heure actuelle, nous l'avons vu -, mais au contraire celle d'un réel essentiellement global - quelque chose comme l'UN de Plotin- mais que nos esprits ne perçoivent que sous les apparences d'une multitude d'objets."
Et sa conclusion finale et magnifique au soir de sa vie. Je te laisse la découvrir.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
F3. Troisième postulat de la mécanique quantique
A chaque propriété observable d'un système physique correspond un opérateur hermitien sur l'espace des états.
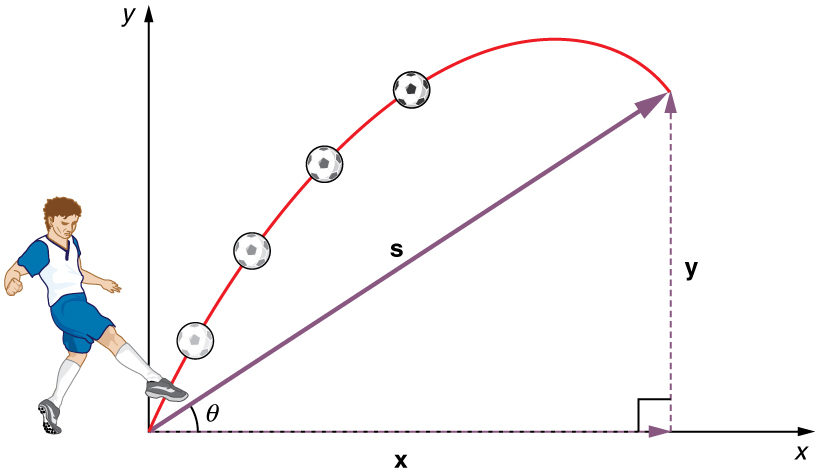
Dans la vie courante, quand on observe un ballon de foot en mouvement, on peut lui assigner toute sorte d'objets mathématiques.
Par exemple, le nombre réel m correspond à sa masse.
Le vecteur s = {6, 5, 0} correspond à sa position dans l'espace à l'heure t=17h57 et 42 secondes.
Ce vecteur forme un angle θ=40° avec l'axe des x.

La vélocité d'un ballon peut elle aussi être décrite par un vecteur à l'instant t (=le temps mesuré à ce moment). La longueur du vecteur correspond à la vitesse qu'on connaît bien, en kilomètre par heure, ou en mètre par seconde. (Autrement dit : 60 km/h est une vitesse, et 60 km/h vers le Nord contient les informations vitesse + une direction dans l'espace = un vecteur vélocité).
En multipliant la masse du ballon par le vecteur vitesse on obtient un autre vecteur qui se nomme la quantité de mouvement. Un ballon ou un train qui fonce sur nous à la même vitesse n'ont pas la même quantité de mouvement, on le pressent intuitivement au moment de l'impact avec eux et nous !
En combinant la position et la quantité de mouvement d'un objet, comme un pendule, on obtient une vision d'ensemble du mouvement du pendule, comme dans les graphiques ci-dessous, qu'on nomme espace des phases.

En effet, à l'horizontale on note la position du pendule entièrement décrite par l'angle θ. Par exemple, le pendule A est dessiné à -30° par rapport à la position de repos du pendule. A la verticale on note sa vitesse.
Dans le laboratoire, le pendule ocille de gauche à droite, sans tourner. Dans l'espace de phase dessiné sur papier, sa trajectoire décrit un cercle, une spirale, une ellipse. Les deux pendules A et B n'ont pas le même comportement, on le voit bien dans l'espace de phase où le premier s'arrête, tandis que le deuxième semble avoir un mouvement perpétuel.
De plus, à chaque fois qu'un pendule se trouve à une extrémité de son mouvement, sa vitesse est alors nulle (on le voit dans l'espace de phase quand la trajectoire intersecte l'axe horizontal), et sa vitesse est au plus haut lorsque θ est nulle, c'est-à-dire lorsque le pendule se trouve en position verticale).
Le troisième postulat stipule que tralala les particlondes ne peuvent pas être décrites de la même manière que les objets de notre quotidien, mais qu'on doit recourir à des opérateurs. (Et en plus, position et vitesse d'une particlonde ne peuvent pas être mesurés précisément en même temps, donc pas d'espace de phase qui montre en un clin d'oeil l'évolution de son mouvement !)
Dans le cas du spin qui nous intéresse, ces opérateurs prennent la forme de matrices comme ci-dessous :
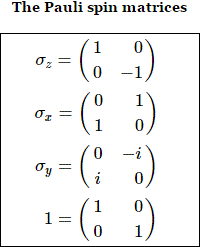
A chaque propriété observable d'un système physique correspond un opérateur hermitien sur l'espace des états.

Dans la vie courante, quand on observe un ballon de foot en mouvement, on peut lui assigner toute sorte d'objets mathématiques.
Par exemple, le nombre réel m correspond à sa masse.
Le vecteur s = {6, 5, 0} correspond à sa position dans l'espace à l'heure t=17h57 et 42 secondes.
Ce vecteur forme un angle θ=40° avec l'axe des x.
La vélocité d'un ballon peut elle aussi être décrite par un vecteur à l'instant t (=le temps mesuré à ce moment). La longueur du vecteur correspond à la vitesse qu'on connaît bien, en kilomètre par heure, ou en mètre par seconde. (Autrement dit : 60 km/h est une vitesse, et 60 km/h vers le Nord contient les informations vitesse + une direction dans l'espace = un vecteur vélocité).
En multipliant la masse du ballon par le vecteur vitesse on obtient un autre vecteur qui se nomme la quantité de mouvement. Un ballon ou un train qui fonce sur nous à la même vitesse n'ont pas la même quantité de mouvement, on le pressent intuitivement au moment de l'impact avec eux et nous !
En combinant la position et la quantité de mouvement d'un objet, comme un pendule, on obtient une vision d'ensemble du mouvement du pendule, comme dans les graphiques ci-dessous, qu'on nomme espace des phases.

En effet, à l'horizontale on note la position du pendule entièrement décrite par l'angle θ. Par exemple, le pendule A est dessiné à -30° par rapport à la position de repos du pendule. A la verticale on note sa vitesse.
Dans le laboratoire, le pendule ocille de gauche à droite, sans tourner. Dans l'espace de phase dessiné sur papier, sa trajectoire décrit un cercle, une spirale, une ellipse. Les deux pendules A et B n'ont pas le même comportement, on le voit bien dans l'espace de phase où le premier s'arrête, tandis que le deuxième semble avoir un mouvement perpétuel.
De plus, à chaque fois qu'un pendule se trouve à une extrémité de son mouvement, sa vitesse est alors nulle (on le voit dans l'espace de phase quand la trajectoire intersecte l'axe horizontal), et sa vitesse est au plus haut lorsque θ est nulle, c'est-à-dire lorsque le pendule se trouve en position verticale).
Le troisième postulat stipule que tralala les particlondes ne peuvent pas être décrites de la même manière que les objets de notre quotidien, mais qu'on doit recourir à des opérateurs. (Et en plus, position et vitesse d'une particlonde ne peuvent pas être mesurés précisément en même temps, donc pas d'espace de phase qui montre en un clin d'oeil l'évolution de son mouvement !)
Dans le cas du spin qui nous intéresse, ces opérateurs prennent la forme de matrices comme ci-dessous :
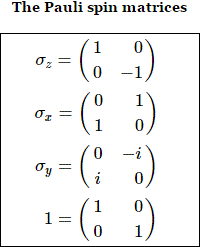
Dernière édition par tim9.5 le Dim 24 Juin 2018 - 11:39, édité 1 fois

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Un gros bravo à Tim pour ses efforts de vulgarisations. C'est difficile de tenter de navigation entre la sursimplification et l'hermétisme .
Je aussi donne mon appui à Cuicui et à Confiteor, et à Hobb bien sûr et sinon je pense que je me retire parce que sinon ça va trop me fatiguer de me fâcher. Et c'est interessant et triste de voir que parler de mécanique quantique tourne à la confiture et quand suite on doive retourner plus vite pour sauver la mayonnaise. Je ne sais pas comment parler de mécanique quantique (et de science tout court)à la plèbe ignorante, aux citoyens curieux. (ainsi qu'aux autres. )
Bref, bon courage à tous, et à la prochaine
Je aussi donne mon appui à Cuicui et à Confiteor, et à Hobb bien sûr et sinon je pense que je me retire parce que sinon ça va trop me fatiguer de me fâcher. Et c'est interessant et triste de voir que parler de mécanique quantique tourne à la confiture et quand suite on doive retourner plus vite pour sauver la mayonnaise. Je ne sais pas comment parler de mécanique quantique (et de science tout court)
Bref, bon courage à tous, et à la prochaine

Badak- Messages : 1230
Date d'inscription : 02/12/2011
Localisation : Montréal
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Transformer de la confiture en mayonnaise, le tout à partir de la mécanique quantique ?!? Ouarf ! On dirait de l'alchimie !Et c'est interessant et triste de voir que parler de mécanique quantique tourne à la confiture et quand suite on doive retourner plus vite pour sauver la mayonnaise.
Tu nous fais une petite video avec dégustation à la fin ?
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Merci pour vos encouragements à tous. Continuons !
F3. Intermède matriciel
Une matrice n'est rien d'autre qu'un sac à main bien rangé (oxymore?). Par exemple la matrice de Pauli sigma-z (voir ci-dessus), peut-être vue comme
a) un arrangement de 4 nombres
b) 2 lignes contenant 2 nombres
c) 2 colonnes contenant 2 nombres
d) une diagonale descendante, de gauche à droite. Si on plie la matrice selon cette diagonale, on observe une certaine symétrie. Dans les matrices sigma-z et 1, le 0 va sur le 0. Dans la matrice sigma-x, le 1 va sur le 1, et dans σy le i vas sur -i. Ce type particulier de matrice symétrique est dite hermitienne. Plus précisément, quand on plie une matrice hermitienne, les nombres qui se chevauchent doivent être ...égaux conjugués : a+bi doit aller sur a-bi.
(Une particularité du langage scientifique est l'abus d'anthroponymes. En effet, les matrices hermitiennes portent ce nom en hommage au mathématicien Charles Hermite. En mécanique quantique on rencontrera aussi l'hamiltonien, le lagrangien, les séries de Fourier, sans parler des espaces hilbertiens maintenant familiers.)
De manière générale, une matrice s'écrit :

Cette notation indicielle pour se repérer dans une matrice qui peut contenir des milliers de colonnes créent en général une frayeur chez des étudiants universitaires lorsque le professeur les assomme hebdomadairement durant 2 heures de cours d'algèbre linéaire à la suite. En effet, au lieu de dessiner de grandes parenthèses avec des nombres flottants à l'intérieur, on utilise en général l'écriture suivante, plus compacte :

L'indice i (qui n'est pas le i au carré = -1) indique la ième ligne de la matrice, tandis que j indique la jème colonne de la matrice.
Avec cette écriture compacte, une matrice est hermitienne si pour tout i et j parcourant la matrice.
pour tout i et j parcourant la matrice.
On compare parfois les mathématiques à la poésie, qui sont tout deux un condensé d'idées, comme l'a fait récemment Cédric V : tous les mots comptent dans le discours, et il ne faut pas en rater un, sous peine d'incompréhension totale. Pour éditer du texte mathématique, les chercheurs ont recours au programme typographique nommé LaTeχ qu'on prononce latek, car ce n'est pas un x, c'est un khi ! (hihihi).
Sur ce forum, j'utiliserai la typographie de wolframalpha, comme à notre habitude.
1) Multiplier un vecteur par une matrice.
Une matrice M peut être vue comme une machine qui transforme un vecteur v en un autre vecteur v' (v prime).
Ce calcul se note ainsi : Mv = v' (la matrice M fois le vecteur v donne le vecteur v').
Exemple :
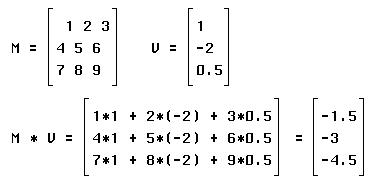
Rien de compliqué, il suffit de multiplier chaque ligne de la matrice par le vecteur v comme tu sais déjà le faire. Pour s'y retrouver on utilise ses deux index. L'index de la main gauche parcourt la premiere ligne de la matrice, tandis que l'index droit parcourt le vecteur du haut vers le bas. Multiplie les nombres qui sont sous tes doigts, puis additionne le résultat au résultat obtenu auparavant. Ensuite avance tes doigts d'un cran, l'index gauche vers la droite et l'index droit vers le bas.
De manière poétique la multiplication se définit ainsi (le premier symbole "A à l'envers" veut dire "pour tout". Donc pour i=1 et j=1, puis pour i=1 et j=2 etc.)

Mais si tu regarde bien, c'est une multiplication entre deux matrices (aij) et (bij), au lieu d'une matrice (aij) et d'un vecteur (bj). Il suffit d'enlever le "j" à bkj et aux b1j, b2j etc. Si ta tête est prête à exploser, c'est normal !
Bref, passons à l'utilisation de la calculette Wolfram pour t'éviter de fuir à tout jamais ce forum.
La matrice M s'écrit {{1,2,3},{4,5,6},{7,8,9}} des objets dans des objets comme dans un sac à main. Le vecteur v vaut {1,-2,0.5} et le résultat de la multiplication vaut {{1,2,3},{4,5,6},{7,8,9}}.{1,-2,0.5} . Attention aux virgules, les ordinateurs ne supportent pas l'imprécision. On obtient bien le vecteur ci-dessus.
En résumé, les transformations linéaires matricielles en vidéo, dans un cadre géométrique (et sans nombre imaginaire. Attention, dans cette vidéo i et j sont des vecteurs de longueur 1 (des vecteurs unitaires). Pour indiquer que ce sont des vecteurs, on surmonte ces lettres d'une flèche. Et dans le cadre de la mécanique quantique, on les écrit li> et lj>.)
F3. Intermède matriciel
Une matrice n'est rien d'autre qu'un sac à main bien rangé (oxymore?). Par exemple la matrice de Pauli sigma-z (voir ci-dessus), peut-être vue comme
a) un arrangement de 4 nombres
b) 2 lignes contenant 2 nombres
c) 2 colonnes contenant 2 nombres
d) une diagonale descendante, de gauche à droite. Si on plie la matrice selon cette diagonale, on observe une certaine symétrie. Dans les matrices sigma-z et 1, le 0 va sur le 0. Dans la matrice sigma-x, le 1 va sur le 1, et dans σy le i vas sur -i. Ce type particulier de matrice symétrique est dite hermitienne. Plus précisément, quand on plie une matrice hermitienne, les nombres qui se chevauchent doivent être ...
(Une particularité du langage scientifique est l'abus d'anthroponymes. En effet, les matrices hermitiennes portent ce nom en hommage au mathématicien Charles Hermite. En mécanique quantique on rencontrera aussi l'hamiltonien, le lagrangien, les séries de Fourier, sans parler des espaces hilbertiens maintenant familiers.)
De manière générale, une matrice s'écrit :
Cette notation indicielle pour se repérer dans une matrice qui peut contenir des milliers de colonnes créent en général une frayeur chez des étudiants universitaires lorsque le professeur les assomme hebdomadairement durant 2 heures de cours d'algèbre linéaire à la suite. En effet, au lieu de dessiner de grandes parenthèses avec des nombres flottants à l'intérieur, on utilise en général l'écriture suivante, plus compacte :

L'indice i (qui n'est pas le i au carré = -1) indique la ième ligne de la matrice, tandis que j indique la jème colonne de la matrice.
Avec cette écriture compacte, une matrice est hermitienne si
 pour tout i et j parcourant la matrice.
pour tout i et j parcourant la matrice.On compare parfois les mathématiques à la poésie, qui sont tout deux un condensé d'idées, comme l'a fait récemment Cédric V : tous les mots comptent dans le discours, et il ne faut pas en rater un, sous peine d'incompréhension totale. Pour éditer du texte mathématique, les chercheurs ont recours au programme typographique nommé LaTeχ qu'on prononce latek, car ce n'est pas un x, c'est un khi ! (hihihi).
Sur ce forum, j'utiliserai la typographie de wolframalpha, comme à notre habitude.
1) Multiplier un vecteur par une matrice.
Une matrice M peut être vue comme une machine qui transforme un vecteur v en un autre vecteur v' (v prime).
Ce calcul se note ainsi : Mv = v' (la matrice M fois le vecteur v donne le vecteur v').
Exemple :
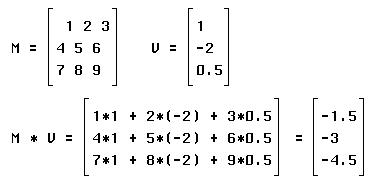
Rien de compliqué, il suffit de multiplier chaque ligne de la matrice par le vecteur v comme tu sais déjà le faire. Pour s'y retrouver on utilise ses deux index. L'index de la main gauche parcourt la premiere ligne de la matrice, tandis que l'index droit parcourt le vecteur du haut vers le bas. Multiplie les nombres qui sont sous tes doigts, puis additionne le résultat au résultat obtenu auparavant. Ensuite avance tes doigts d'un cran, l'index gauche vers la droite et l'index droit vers le bas.
De manière poétique la multiplication se définit ainsi (le premier symbole "A à l'envers" veut dire "pour tout". Donc pour i=1 et j=1, puis pour i=1 et j=2 etc.)

Mais si tu regarde bien, c'est une multiplication entre deux matrices (aij) et (bij), au lieu d'une matrice (aij) et d'un vecteur (bj). Il suffit d'enlever le "j" à bkj et aux b1j, b2j etc. Si ta tête est prête à exploser, c'est normal !
Bref, passons à l'utilisation de la calculette Wolfram pour t'éviter de fuir à tout jamais ce forum.
La matrice M s'écrit {{1,2,3},{4,5,6},{7,8,9}} des objets dans des objets comme dans un sac à main. Le vecteur v vaut {1,-2,0.5} et le résultat de la multiplication vaut {{1,2,3},{4,5,6},{7,8,9}}.{1,-2,0.5} . Attention aux virgules, les ordinateurs ne supportent pas l'imprécision. On obtient bien le vecteur ci-dessus.
En résumé, les transformations linéaires matricielles en vidéo, dans un cadre géométrique (et sans nombre imaginaire. Attention, dans cette vidéo i et j sont des vecteurs de longueur 1 (des vecteurs unitaires). Pour indiquer que ce sont des vecteurs, on surmonte ces lettres d'une flèche. Et dans le cadre de la mécanique quantique, on les écrit li> et lj>.)

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
F4. Quatrième postulat (sur 6)
Les résultats possibles de la mesure d'une variable dynamique sont les valeurs propres de l'observable correspondante (p.36)
Ce postulat et le 5ème lient les matrices qu'on a appelées "opérateurs" avec les résultats d'une expérience de laboratoire.
Zoom sur les matrices
On a vu au post précédent que les matrices pouvaient être vues comme une collection de nombres bien rangées - un sac à main. Et elles ont plusieurs tours dans leur sac ! En effet, à partir d'une matrice on peut faire apparaître des vecteurs et des nombres spéciaux, appelés vecteurs propres et valeurs propres (ici propre ≠ sale, mais propre = qui appartient à la matrice).
De 1 min 20 à 4 minutes de cette vidéo, 3Blue1Brown propose de visualiser les valeurs propres et les vecteurs propres d'une matrice de petite taille. Pour faire court, une matrice 2x2 transforme le plan en laissant certaines droites invariantes, en rose dans la vidéo. Connaître les vecteurs propres de la matrice permet de trouver directement ces droites immobiles durant la transformation opérée par la matrice.
Mathématiquement, un vecteur propre v et une valeur propre λ (lambda, un nombre réel) d'une matrice A vérifie la propriété suivante : A fois v = λ fois v, ou, en cachant les fois Av = λv.
La suite de la vidéo explique comment calculer les λ et les v, qui demandent toutefois des prérequis multimédias indiqués dans la première minute de la vidéo. Les mathématiques sous-jacentes ne sont pas compliquées, mais je préfère utiliser un raccourci calculatoire : wolframalpha.
Reprenons l'opérateur σz ("sigma zède") vue au §F.3, qui est la première matrice de spin de Pauli = {{1,0},{0,-1}}, que tu copies dans wolfram : http://www.wolframalpha.com/input/?i=%7B%7B1,0%7D,%7B0,-1%7D%7D. Fais défiler la page pour tomber sur les réponses "eigenvalues" et "eigenvector".
On vérifie que
a) pour λ = 1 et le vecteur v = {1,0}, on ait bien Av = λv c'est-à-dire {{1,0},{0,-1}}.{1,0} = 1{1,0}
b) pour λ = -1 et le vecteur v = {0,1}, on ait bien Av = λv c'est-à-dire {{1,0},{0,-1}}.{0,1} = -1{0,1}.
Ca ne te rappelles-rien ?


Reprenons le 4ème postulat dans le cas du Stern-Gerlach : il y a deux résultats possibles pour un électron qui passe à travers un champ magnétique. Soit il monte en passant par le chemin rouge, soit il descent par le chemin bleu. Soit il s'écrase vers le haut (+1), soit vers le bas. (-1). +1 et -1 sont les valeurs propres de l'opérateur σz.
Le 5ème postulat fera intervenir les ... vecteurs propres de l'opérateur.
Les résultats possibles de la mesure d'une variable dynamique sont les valeurs propres de l'observable correspondante (p.36)
Ce postulat et le 5ème lient les matrices qu'on a appelées "opérateurs" avec les résultats d'une expérience de laboratoire.
Zoom sur les matrices
On a vu au post précédent que les matrices pouvaient être vues comme une collection de nombres bien rangées - un sac à main. Et elles ont plusieurs tours dans leur sac ! En effet, à partir d'une matrice on peut faire apparaître des vecteurs et des nombres spéciaux, appelés vecteurs propres et valeurs propres (ici propre ≠ sale, mais propre = qui appartient à la matrice).
De 1 min 20 à 4 minutes de cette vidéo, 3Blue1Brown propose de visualiser les valeurs propres et les vecteurs propres d'une matrice de petite taille. Pour faire court, une matrice 2x2 transforme le plan en laissant certaines droites invariantes, en rose dans la vidéo. Connaître les vecteurs propres de la matrice permet de trouver directement ces droites immobiles durant la transformation opérée par la matrice.
Mathématiquement, un vecteur propre v et une valeur propre λ (lambda, un nombre réel) d'une matrice A vérifie la propriété suivante : A fois v = λ fois v, ou, en cachant les fois Av = λv.
La suite de la vidéo explique comment calculer les λ et les v, qui demandent toutefois des prérequis multimédias indiqués dans la première minute de la vidéo. Les mathématiques sous-jacentes ne sont pas compliquées, mais je préfère utiliser un raccourci calculatoire : wolframalpha.
Reprenons l'opérateur σz ("sigma zède") vue au §F.3, qui est la première matrice de spin de Pauli = {{1,0},{0,-1}}, que tu copies dans wolfram : http://www.wolframalpha.com/input/?i=%7B%7B1,0%7D,%7B0,-1%7D%7D. Fais défiler la page pour tomber sur les réponses "eigenvalues" et "eigenvector".
On vérifie que
a) pour λ = 1 et le vecteur v = {1,0}, on ait bien Av = λv c'est-à-dire {{1,0},{0,-1}}.{1,0} = 1{1,0}
b) pour λ = -1 et le vecteur v = {0,1}, on ait bien Av = λv c'est-à-dire {{1,0},{0,-1}}.{0,1} = -1{0,1}.
Ca ne te rappelles-rien ?

Reprenons le 4ème postulat dans le cas du Stern-Gerlach : il y a deux résultats possibles pour un électron qui passe à travers un champ magnétique. Soit il monte en passant par le chemin rouge, soit il descent par le chemin bleu. Soit il s'écrase vers le haut (+1), soit vers le bas. (-1). +1 et -1 sont les valeurs propres de l'opérateur σz.
Le 5ème postulat fera intervenir les ... vecteurs propres de l'opérateur.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
La décomposition spectrale
Newton est connu pour ses expériences avec des prismes, en faisant y passer un rayon lumineux du soleil. La lumière "blanche" se décompose alors en lumières colorées.

A la place de prisme, on peut utiliser un spectroscope, dont la pièce maîtresse est un réseau de fentes.


Au centre de l'écran, en position I, est la lumière telle qu'on l'a perçoit, et de part et d'autres, des lignes verticales colorées qu'on nomme spectre de la lumière étudiée.

Si on regarde des gaz chauffés, leurs spectres sont bien définis. Les raies de lumières sont transformées en nombres λ mesurés en nanomètres, appelés longueur d'onde. Ce processus s'appelle "décomposition spectrale" de la lumière, qui est bien plus joyeux que les spectres cinématrographiques !.
Pour plus de détails sur cet aparté : https://www.kartable.fr/ressources/physique-chimie/cours/les-spectres-lumineux/12902
Newton est connu pour ses expériences avec des prismes, en faisant y passer un rayon lumineux du soleil. La lumière "blanche" se décompose alors en lumières colorées.

A la place de prisme, on peut utiliser un spectroscope, dont la pièce maîtresse est un réseau de fentes.


Au centre de l'écran, en position I, est la lumière telle qu'on l'a perçoit, et de part et d'autres, des lignes verticales colorées qu'on nomme spectre de la lumière étudiée.

Si on regarde des gaz chauffés, leurs spectres sont bien définis. Les raies de lumières sont transformées en nombres λ mesurés en nanomètres, appelés longueur d'onde. Ce processus s'appelle "décomposition spectrale" de la lumière, qui est bien plus joyeux que les spectres cinématrographiques !.
Pour plus de détails sur cet aparté : https://www.kartable.fr/ressources/physique-chimie/cours/les-spectres-lumineux/12902

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Décomposition spectrale d'une matrice

Par analogie, au lieu de décomposer une lumière pour connaître ses couleurs fondamentales, on décompose un opérateur pour connaître ses valeurs et vecteurs propres. L'ensemble des valeurs propres d'une matrice s'appelle le spectre de la matrice.
Notation : pour toute valeur propre λ on notera lλ> son vecteur propre correspondant.
Probabilité conditionnelle
Tout le monde connaît la probabilité d'obtenir un "5" à l'aide d'un dé. C'est le nombre de cas
souhaîtés divisé par le nombre de cas possibles proposé par le dé. Ce qui revient à 1 chance sur 6, ou 1/6, ou 0.17.
De même, tirer un 2 de trèfle dans un paquet de 52 cartes a pour probabilité 1/52. On écrit en abrégé P(2 de trèfle) = 1/52. P pour probabilité.
David est un magicien renommé. Pour lui, ça se passe différemment. Il me propose de tirer une carte dans son paquet, et voilà que le 2 de trèfle sort. (1 chance sur 52 si le paquet de carte n'est pas biaisé).
Maintenant, quelle est la probabilité que David tire le 2 de trèfle sachant que c'est celle que j'ai tiré juste avant ? Elle est de 100% puisqu'il est magicien, comme dans le premier tour de magie de la vidéo.
Ce type de probabilité se nomme probabilité conditionnelle. P(2 de trèfle sachant qu'elle a été tirée avant) = P(2 de trèfle |2 de trèfle). La barre verticale signifie "sachant que".
Cinquième postulat
Dans l'exemple du spin :
la probabilité qu'une mesure du spin donne le nombre réel λ, sachant que le spin est dans l'état lψ>
= P(spin → λ ⎢ψ)
= <λ⎢ψ> au carré, divisé par <λ⎢λ><ψ⎢ψ>
= <λ⎢ψ>²/(<λ⎢λ><ψ⎢ψ>)
De plus, l'état lψ> du spin juste après la mesure sera nécessairement l'un des vecteurs propres de l'hamiltonien.
Waouh ! Ca pique les yeux ! Un exemple.


On veut mesurer la valeur que prend le spin d'un atome sur l'axe vertical z. On choisit donc l'opérateur σz qui a pour valeur propre +1 relié au vecteur propre ⎢+1>={1,0}, dont le conjugué vaut <+1⎢={1,0} (on change simplement les signes des nombres imaginaires).
L'état du spin avant la mesure s'écrit de manière général ⎢ψ>={α,β} selon l'image de droite, avec α² + β² = 1 puisque le vecteur est sur le cercle de rayon 1.
Remarque : les vecteurs ⎢+1> et ⎢ψ> sont de longueur 1. Donc <+1⎢+1>= {1,0}.{1,0} = 1 et <ψ⎢ψ>= {a,b}.{a,b} = α² + β² = 1
La probabilité que l'atome prenne le chemin rouge +1, sachant qu'il est dans l'état⎢ψ>
= P(spin → +1 ⎢ψ)
= <+1⎢ψ> au carré, divisé par (<+1⎢+1> <ψ⎢ψ>)
={{1,0}.{α,β}} au carré, divisé par 1 = α au carré.
De même, P(spin → -1 ⎢ψ) = <-1⎢ψ> au carré = {{0,1}.{α,β}} au carré = β au carré.
Ce sont bien les résultats obtenus dans la section du 30 mai.
De plus, l'état ⎢ψ> du spin sera après la mesure soit ⎢+1>={1,0}, soit ⎢-1>={0,1}. (Lorsque la probabilité est de 100%, il n'y a pas de changement possible pour le vecteur d'état. Il reste comme il est.)

Par analogie, au lieu de décomposer une lumière pour connaître ses couleurs fondamentales, on décompose un opérateur pour connaître ses valeurs et vecteurs propres. L'ensemble des valeurs propres d'une matrice s'appelle le spectre de la matrice.
Notation : pour toute valeur propre λ on notera lλ> son vecteur propre correspondant.
Probabilité conditionnelle
Tout le monde connaît la probabilité d'obtenir un "5" à l'aide d'un dé. C'est le nombre de cas
souhaîtés divisé par le nombre de cas possibles proposé par le dé. Ce qui revient à 1 chance sur 6, ou 1/6, ou 0.17.
De même, tirer un 2 de trèfle dans un paquet de 52 cartes a pour probabilité 1/52. On écrit en abrégé P(2 de trèfle) = 1/52. P pour probabilité.
David est un magicien renommé. Pour lui, ça se passe différemment. Il me propose de tirer une carte dans son paquet, et voilà que le 2 de trèfle sort. (1 chance sur 52 si le paquet de carte n'est pas biaisé).
Maintenant, quelle est la probabilité que David tire le 2 de trèfle sachant que c'est celle que j'ai tiré juste avant ? Elle est de 100% puisqu'il est magicien, comme dans le premier tour de magie de la vidéo.
Ce type de probabilité se nomme probabilité conditionnelle. P(2 de trèfle sachant qu'elle a été tirée avant) = P(2 de trèfle |2 de trèfle). La barre verticale signifie "sachant que".
Cinquième postulat
Dans l'exemple du spin :
la probabilité qu'une mesure du spin donne le nombre réel λ, sachant que le spin est dans l'état lψ>
= P(spin → λ ⎢ψ)
= <λ⎢ψ> au carré, divisé par <λ⎢λ><ψ⎢ψ>
= <λ⎢ψ>²/(<λ⎢λ><ψ⎢ψ>)
De plus, l'état lψ> du spin juste après la mesure sera nécessairement l'un des vecteurs propres de l'hamiltonien.
Waouh ! Ca pique les yeux ! Un exemple.

On veut mesurer la valeur que prend le spin d'un atome sur l'axe vertical z. On choisit donc l'opérateur σz qui a pour valeur propre +1 relié au vecteur propre ⎢+1>={1,0}, dont le conjugué vaut <+1⎢={1,0} (on change simplement les signes des nombres imaginaires).
L'état du spin avant la mesure s'écrit de manière général ⎢ψ>={α,β} selon l'image de droite, avec α² + β² = 1 puisque le vecteur est sur le cercle de rayon 1.
Remarque : les vecteurs ⎢+1> et ⎢ψ> sont de longueur 1. Donc <+1⎢+1>= {1,0}.{1,0} = 1 et <ψ⎢ψ>= {a,b}.{a,b} = α² + β² = 1
La probabilité que l'atome prenne le chemin rouge +1, sachant qu'il est dans l'état⎢ψ>
= P(spin → +1 ⎢ψ)
= <+1⎢ψ> au carré, divisé par (<+1⎢+1> <ψ⎢ψ>)
={{1,0}.{α,β}} au carré, divisé par 1 = α au carré.
De même, P(spin → -1 ⎢ψ) = <-1⎢ψ> au carré = {{0,1}.{α,β}} au carré = β au carré.
Ce sont bien les résultats obtenus dans la section du 30 mai.
De plus, l'état ⎢ψ> du spin sera après la mesure soit ⎢+1>={1,0}, soit ⎢-1>={0,1}. (Lorsque la probabilité est de 100%, il n'y a pas de changement possible pour le vecteur d'état. Il reste comme il est.)
Dernière édition par tim9.5 le Mer 4 Juil 2018 - 18:11, édité 2 fois

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Un autre exemple qui explicite la démarche des 5 postulats
Prenons un atome de spin dans l'état +1 selon l'axe z, qu'on notera l+z>. Quelle est la probabilité que le spin prenne la valeur +1 selon l'axe x?
Prenons un atome de spin dans l'état +1 selon l'axe z, qu'on notera l+z>. Quelle est la probabilité que le spin prenne la valeur +1 selon l'axe x?
- Corrigé:
a) Pour obtenir un atome dont le spin est dans l'état l+z>, il suffit de le faire passer par le stern-gerlach. S'il passe par le chemin rouge, son spin est alors forcément à l'état voulu. Sinon, on prend un deuxième candidat et on répète la procédure.
Sur l'animation PhET ci-dessus, il suffit donc de sélectionner +z.
Les postulats 1 et 2 de la mécanique quantique disent que cet état existe dans un espace hilbertien.
b) Que signifie "selon l'axe z", "selon l'axe x" ?
Pour y répondre, modélisons le champ magnétique crée entre les deux pôles aimantés du stern-gerlach par une flèche notée ∂B/∂z sur l'image. La question devient :"Le spin de l'atome vaut +1 quand la flèche ∂B/∂z est alignée sur l'axe z. Quelle est la probabilité d'obtenir +1 lorsque l'atome passe à travers un champ magnétique aligné cette fois-ci sur l'axe x?" Ce qui revient à tourner le stern-gerlach de 90°.
c) Le postulat 3 demande de choisir le bon opérateur. Cette fois-ci on sélectionne la matrice de Pauli σx qui mesure le spin selon l'axe x. Elle se note {{0,1},{1,0}} (voir le post du sa 23 juin).
d) Le 4ème postulat stipule de calculer les valeurs propres et les vecteurs propres de l'opérateur (Wolfram, à l'aide!) ce qui nous donne le vecteur propre {1,1} pour la valeur propre +1.
e) D'après le 5ème postulat, P(obtenir +1 sur l'axe x ⎢on a eu +1 sur l'axe z) = {1,1}.{0,1} au carré / ({1,1}.{1,1} fois {0,1}.{0,1})= 1/(2 fois 1) = 1/2.
Résultat déjà vu avec le stern-gerlach.

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Faire le point sur quantum for dummies, season 1
La section B p.10 présente quelques outils mathématiques pour appréhender l'espace de Hilbert.
La section D p.11-12 s'attarde sur l'expérience historique de Stern-Gerlach sur la mesure du spin, avec un point de vue plutôt géométrique sur les spinneurs.
La section E est un interlude sur les nombres complexes, pour arriver à la section F qui présente les postutats de la mécanique quantique.
Donc plusieurs manières d'aborder la mécanique quantique :
- par de la géométrie (cercle, perpendiculaires, projection) qui fonctionne relativement bien pour le système le plus simple, celui à deux états.
- par des matrices, utilisées par Heisenberg
- par des ondes (qu'on verra au postulat 6), les mythiques ondes de Schrödinger.

- par du formalisme (état lψ>, opérateur désigné par une majuscule, produit scalaire <φlψ>), introduit par Paul Dirac, qui permet de faire le lien entre la version matricielle d'Heisenberg et celle de Schrödinger.
Chacun a ses avantages et ses inconvénients. La version matricielle est très utile pour des systèmes qui dont les résultats possibles sont en nombre fini. Elle demande néanmoins d'entrer dans un monde mathématique matriciel qui n'a pas forcément un support visuel pour bien comprendre ce qu'il se passe réellement. En revanche, l'écriture matricielle s'implémente aisément dans un ordinateur, ce qui permettra dans des cas simples d'obtenir des simulations sympathiques. (au fait, dès que tu fais par exemple une rotation de ton avatar dans ton jeu préféré, tu utilises automatiquement une matrice cachée dans le programme !)
A cause de cette abstraction, les physiciens d'il y a bientôt 100 ans préférèrent le développement ondulatoire de Schrödinger. Mais sa simplicité visuelle n'est qu'apparente, et elle demande de connaître d'autres outils mathématiques non encore abordés dans ce fil.
Finalement, vers 1980, le spin de l'électron revint à la mode pour se généraliser en qbit, la plus petite unité porteuse d'information dans un ordinateur quantique. Une autre approche visuelle apparut pour modéliser le spin.
Je vous propose donc, ami lecteur virtuel (donc moi-même si je solliloque ), de rester quelque peu dans le formalisme matriciel (aïe, des maths !), pour pouvoir bifurquer vers le qubit avant de s'attaquer au 6ème postulat, en passant par quelques bizarreries quantiques comme on les aime.
), de rester quelque peu dans le formalisme matriciel (aïe, des maths !), pour pouvoir bifurquer vers le qubit avant de s'attaquer au 6ème postulat, en passant par quelques bizarreries quantiques comme on les aime.
La section B p.10 présente quelques outils mathématiques pour appréhender l'espace de Hilbert.
La section D p.11-12 s'attarde sur l'expérience historique de Stern-Gerlach sur la mesure du spin, avec un point de vue plutôt géométrique sur les spinneurs.
La section E est un interlude sur les nombres complexes, pour arriver à la section F qui présente les postutats de la mécanique quantique.
Donc plusieurs manières d'aborder la mécanique quantique :
- par de la géométrie (cercle, perpendiculaires, projection) qui fonctionne relativement bien pour le système le plus simple, celui à deux états.
- par des matrices, utilisées par Heisenberg
- par des ondes (qu'on verra au postulat 6), les mythiques ondes de Schrödinger.

- par du formalisme (état lψ>, opérateur désigné par une majuscule, produit scalaire <φlψ>), introduit par Paul Dirac, qui permet de faire le lien entre la version matricielle d'Heisenberg et celle de Schrödinger.
Chacun a ses avantages et ses inconvénients. La version matricielle est très utile pour des systèmes qui dont les résultats possibles sont en nombre fini. Elle demande néanmoins d'entrer dans un monde mathématique matriciel qui n'a pas forcément un support visuel pour bien comprendre ce qu'il se passe réellement. En revanche, l'écriture matricielle s'implémente aisément dans un ordinateur, ce qui permettra dans des cas simples d'obtenir des simulations sympathiques. (au fait, dès que tu fais par exemple une rotation de ton avatar dans ton jeu préféré, tu utilises automatiquement une matrice cachée dans le programme !)
A cause de cette abstraction, les physiciens d'il y a bientôt 100 ans préférèrent le développement ondulatoire de Schrödinger. Mais sa simplicité visuelle n'est qu'apparente, et elle demande de connaître d'autres outils mathématiques non encore abordés dans ce fil.
Finalement, vers 1980, le spin de l'électron revint à la mode pour se généraliser en qbit, la plus petite unité porteuse d'information dans un ordinateur quantique. Une autre approche visuelle apparut pour modéliser le spin.
Je vous propose donc, ami lecteur virtuel (donc moi-même si je solliloque

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
tim9.5 a écrit:
re-Salut, c'est un joli schéma, mais j'avoue que c'est vraiment la première fois que je vois que certains parlent de "Whole numbers" pour parler des nombres naturels avec le zéro. Ça me semble un peu bizarre . Même dans les livres d'analyse en anglais je ne l'ai jamais vu, mais en plus en français je me demande bien comment ça se traduit.
( Et puis pour s'amuser un pe plus, on peut généraliser encore les nombres complexes vers les quaternions, les octonions et autres oignons. mais cela dépasse le niveau de ton cours qui va déjà être assez difficile comme ça pour le niveau de ce forum...

Badak- Messages : 1230
Date d'inscription : 02/12/2011
Localisation : Montréal
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Whole numbers = nombre entiers
integers = nombre entiers relatifs ou nombre relatif. A mon époque on écrivait N* pour exclure le zéro. Mais c'est vrai que ça doit être surtout pour relever l'invention du zéro, selon le souvenir que j'en ai. Faut voir plutôt des bulles qui grossissent de plus en plus, ce qui permet d'introduire peu à peu les nombres.
Autre point de vue, celui des groupes imbriqués (?) : (N sauf zéro,*) puis (N avec zéro, +).
Les nombres complexes n'ont rien de compliqué. On aurait dû les nommer les duognons
Les quaternions sont de plus en plus utilisé pour la 3D, c'est un scalaire + un vecteur. Tip top pour les rotations. En plus c'est facile à écrire : il faut mettre du gras 1 i j k. J'ai trouvé une vidéo avec des tirettes que je ressortirai peut-être.
Dans l'arrière-fond de ma pensée, j'écris pour qu'un enfant de 12 ans hp sois capable de me lire. Pour l'instant ça passe toujours, j'ai un testeur!
Le big problem pour l'instant, c'est SU(2) avec ses représentants innocents (qui a peur du spineur {1,0} ?). Je suis en passe de trouver un chemin. Il y a quelques profs d'uni qui ont écris des articles géniaux ces 5 dernières années sur les spineurs, qu'on trouve aussi cachés fondamentalement en relativité mais qui s'y comportent comme des monstres indomptables et insolents. En méca Q, ils ont l'air plutôt dociles (de loin en tout cas).
Mais bon, SU(2) est tellement fondamental puisqu'il concerne tous les fermions que ça vaut la peine de s'y attarder.
Il y a aussi quelques simulations proposées dans les bas-fond d'internet par des universités.
Ce que j'ai appris des vidéos :
- plus il y a de vue, plus c'est du bogdanov, sauf quelques pointures.
- 4'000 vues c'est pas mal pour une vidéo d'un prof qui écrit au tableau.
- un record : 6 vues d'un cours donné par un prof excellent https://www.youtube.com/watch?v=76pWL5hwh7g. Je trouve que ses slides sont vraiment bien faites, avec des couleurs, des flèches, etc. (et j'ai trouvé quelques slides sympas).
Les octonions, je ne sais pas quelle est leur utilité.
Ensuite, Schrödinger qui fait des vagues, c'est une autre paire de manche !
Merci pour ton retour, ça fait plaisir de te lire !
integers = nombre entiers relatifs ou nombre relatif. A mon époque on écrivait N* pour exclure le zéro. Mais c'est vrai que ça doit être surtout pour relever l'invention du zéro, selon le souvenir que j'en ai. Faut voir plutôt des bulles qui grossissent de plus en plus, ce qui permet d'introduire peu à peu les nombres.
Autre point de vue, celui des groupes imbriqués (?) : (N sauf zéro,*) puis (N avec zéro, +).
Les nombres complexes n'ont rien de compliqué. On aurait dû les nommer les duognons
Les quaternions sont de plus en plus utilisé pour la 3D, c'est un scalaire + un vecteur. Tip top pour les rotations. En plus c'est facile à écrire : il faut mettre du gras 1 i j k. J'ai trouvé une vidéo avec des tirettes que je ressortirai peut-être.
Dans l'arrière-fond de ma pensée, j'écris pour qu'un enfant de 12 ans hp sois capable de me lire. Pour l'instant ça passe toujours, j'ai un testeur!
Le big problem pour l'instant, c'est SU(2) avec ses représentants innocents (qui a peur du spineur {1,0} ?). Je suis en passe de trouver un chemin. Il y a quelques profs d'uni qui ont écris des articles géniaux ces 5 dernières années sur les spineurs, qu'on trouve aussi cachés fondamentalement en relativité mais qui s'y comportent comme des monstres indomptables et insolents. En méca Q, ils ont l'air plutôt dociles (de loin en tout cas).
Mais bon, SU(2) est tellement fondamental puisqu'il concerne tous les fermions que ça vaut la peine de s'y attarder.
Il y a aussi quelques simulations proposées dans les bas-fond d'internet par des universités.
Ce que j'ai appris des vidéos :
- plus il y a de vue, plus c'est du bogdanov, sauf quelques pointures.
- 4'000 vues c'est pas mal pour une vidéo d'un prof qui écrit au tableau.
- un record : 6 vues d'un cours donné par un prof excellent https://www.youtube.com/watch?v=76pWL5hwh7g. Je trouve que ses slides sont vraiment bien faites, avec des couleurs, des flèches, etc. (et j'ai trouvé quelques slides sympas).
Les octonions, je ne sais pas quelle est leur utilité.
Ensuite, Schrödinger qui fait des vagues, c'est une autre paire de manche !
Merci pour ton retour, ça fait plaisir de te lire !

tim9.5- Messages : 451
Date d'inscription : 18/10/2014
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
re-salut. pour la terminologie, je me tiens à Integer = entiers, et natural = naturel. De toute façon c'est possible que certains matheux dans certaines langues utilisent des appellations bizarres, ça se fait toujours, mais comme chacun écrit avec les mêmes symboles, ou donne ses définitions s'il introduit un truc inhabituel, en gros tout le monde se comprend.tim9.5 a écrit:Whole numbers = nombre entiers
integers = nombre entiers relatifs ou nombre relatif. A mon époque on écrivait N* pour exclure le zéro. Mais c'est vrai que ça doit être surtout pour relever l'invention du zéro, selon le souvenir que j'en ai. Faut voir plutôt des bulles qui grossissent de plus en plus, ce qui permet d'introduire peu à peu les nombres.
Autre point de vue, celui des groupes imbriqués (?) : (N sauf zéro,*) puis (N avec zéro, +).
Les nombres complexes n'ont rien de compliqué. On aurait dû les nommer les duognons
Les quaternions sont de plus en plus utilisé pour la 3D, c'est un scalaire + un vecteur. Tip top pour les rotations. En plus c'est facile à écrire : il faut mettre du gras 1 i j k. J'ai trouvé une vidéo avec des tirettes que je ressortirai peut-être.
Dans l'arrière-fond de ma pensée, j'écris pour qu'un enfant de 12 ans hp sois capable de me lire. Pour l'instant ça passe toujours, j'ai un testeur!
Le big problem pour l'instant, c'est SU(2) avec ses représentants innocents (qui a peur du spineur {1,0} ?). Je suis en passe de trouver un chemin. Il y a quelques profs d'uni qui ont écris des articles géniaux ces 5 dernières années sur les spineurs, qu'on trouve aussi cachés fondamentalement en relativité mais qui s'y comportent comme des monstres indomptables et insolents. En méca Q, ils ont l'air plutôt dociles (de loin en tout cas).
Mais bon, SU(2) est tellement fondamental puisqu'il concerne tous les fermions que ça vaut la peine de s'y attarder.
Il y a aussi quelques simulations proposées dans les bas-fond d'internet par des universités.
SU(2), c'est aussi de mes groupes préférés. C'est sûr aussi que si je t'avais eu comme prof à 12 ans j'aurais appris plus vite et davantage, mais je pense que c'est rarement au programme . Je suis toujours agréablement surpris aussi lorsqu'un vrai vulgarisateur veut expliquer les vrais objets mathématiques comme les groupes. Je me suis acheté l'autre jour un petit livre de vulgarisation sur les physique des particules (que je n'ai jamais étudié sérieusement) et l'auteur utilisait les groupes pour décrire le modèle standard et différentes théories des cordes.
Dans tous les cas bonne continuation.
Un autre truc dingue pour une formulation alternative des groupes qui part d'une généralisation des nombres complexes: les groupes de Clifford. Je n'en suis pas vraiment spécialiste, mais c'est une autre approche. Je continue ma lecture du fil à rebours, je vais sûrement revenir.

Badak- Messages : 1230
Date d'inscription : 02/12/2011
Localisation : Montréal
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
C'est avec grande désolation que je me rends compte que les scientifiques se fourvoient une fois de plus... Avez-vous entendu parlé de la psychologie quantique ? C'est Alexandre sur ce site qui m'a fait découvrir. Pour éclairer les gens comme vous, il a traduit un ouvrage entier de Stephen Wolinsky, un disciple du célèbre maître indien Nisargadatta Maharaj !! Pourquoi ne pas lui demander conseil ? A force de trop écouter votre raison et votre mental, vous ne pouvez pas comprendre ce qu'il y a de plus simple, car la Vérité est la simplicité même ! Inutile donc de recourir à des mathématiques compliquées ! Il y a des talents incroyables sur ce forum, pourquoi ne pas les écouter ??? 
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Houlala ! Merci pour cet engouement si le Alexandre en question c'est "moi", mais attention tout de même car je crains que l'emballement soit un poil déplacé ici  .
.
Voici ce que j'avais écrit à propos du mot "quantique" utilisé par Wolinsky quand j'en avais parlé sur un autre sujet (cf. ce message : https://www.zebrascrossing.net/t35357p75-la-philosophie-est-elle-une-spiritualite#1438693) :
La physique quantique de ce sujet est tout à fait respectable et n'a pas à être mélangée à la psychologie (même si, même si... un jour peut-être ?). Pour le moment, ce sont deux univers séparés et différents et il ne peut y avoir que des conséquences très négatives pour la seconde à trop vouloir la rattacher à la première. La science et les scientifiques ne fonctionnent pas ainsi, ils ont leurs manières de penser et leurs méthodes qui ont fait les succès de la science. Les choses doivent continuer d'aller à leur rythme.
Alors bonne continuation quantique, et longue vie à ce sujet !
!
(PS : Faire de la physique n'empêche pas de s'intéresser sincèrement à la spiritualité non plus ...)
...)
Voici ce que j'avais écrit à propos du mot "quantique" utilisé par Wolinsky quand j'en avais parlé sur un autre sujet (cf. ce message : https://www.zebrascrossing.net/t35357p75-la-philosophie-est-elle-une-spiritualite#1438693) :
Alexandre a écrit:
Concernant le mot Quantum que j'ai mis entre parenthèses : dans un autre sujet il y a quelques temps, j'avais évoqué le sujet. Je pense que la référence "à la quantique" est superflue dans tout un mouvement récent qui va de la médecine à, ici, la spiritualité (bien que le titre parle de psychologie dans le livre dont il est question). Je l'ai déjà dit : quand on connaît un peu la science, la physique quantique en particulier, et surtout la susceptibilité des scientifiques, on ne devrait pas coller du quantique à toutes les sauces. Pour certains, il s'agit de "créer" du crédit à ce qu'ils proposent. Tant pis, ils se feront taper sur les doigts à juste titre par les scientifiques. Pour d'autres (comme c'est le cas ici), la référence à la physique quantique entend souligner que la physique moderne est en train de redécouvrir, avec quelques millénaires de retard mais avec l'avantage d'avoir une démarche rationnelle, ce que l'on sait depuis des lustres de façon non rationnelle. Cependant, la science ne peut se satisfaire d'analogies et de parallèles, et ce nouveau quantique n'est donc pas du vrai quantique scientifique... C'est dommage d'avoir cette démarche car ce qui est proposé dans ces nouvelles approches est tellement nouveau que leurs auteurs ne devraient pas en avoir besoin. Mais bon, c'est ainsi...
La physique quantique de ce sujet est tout à fait respectable et n'a pas à être mélangée à la psychologie (même si, même si... un jour peut-être ?). Pour le moment, ce sont deux univers séparés et différents et il ne peut y avoir que des conséquences très négatives pour la seconde à trop vouloir la rattacher à la première. La science et les scientifiques ne fonctionnent pas ainsi, ils ont leurs manières de penser et leurs méthodes qui ont fait les succès de la science. Les choses doivent continuer d'aller à leur rythme.
Alors bonne continuation quantique, et longue vie à ce sujet
(PS : Faire de la physique n'empêche pas de s'intéresser sincèrement à la spiritualité non plus
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Rønin47 a écrit:C'est avec grande désolation que je me rends compte que les scientifiques se fourvoient une fois de plus... Avez-vous entendu parlé de la psychologie quantique ? C'est Alexandre sur ce site qui m'a fait découvrir. Pour éclairer les gens comme vous, il a traduit un ouvrage entier de Stephen Wolinsky, un disciple du célèbre maître indien Nisargadatta Maharaj !! Pourquoi ne pas lui demander conseil ? A force de trop écouter votre raison et votre mental, vous ne pouvez pas comprendre ce qu'il y a de plus simple, car la Vérité est la simplicité même ! Inutile donc de recourir à des mathématiques compliquées ! Il y a des talents incroyables sur ce forum, pourquoi ne pas les écouter ???
Halala, on en lit des conneries, mais là...
Enfin bref, laissez nous nous fourvoyer, à un point tel qu'on a réussi à mettre à votre disposition un pc et internet, pour étaler au monde entier votre ignorance la plus totale en la matière.
Si vous ne comprenez pas (et c'est visiblement le cas), laissez les spécialistes s'en occuper, au lieu de leur donner des leçons.
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Pas du tout ! Il ne faut pas te sous-estimer !!Alexandre a écrit:Houlala ! Merci pour cet engouement si le Alexandre en question c'est "moi", mais attention tout de même car je crains que l'emballement soit un poil déplacé ici.
La science découle de la philosophie, tes critiques contre la philosophie sont donc parfaitement recevables ici !
Et la psychologie est aussi de la science ! Si les scientifiques se fourvoient, alors pourquoi ne pas les aider ?
Hobb n'a pas lu l'oeuvre de Wolinsky, d'où sa réaction réfractaire...
Pourquoi ne pas l'amener à évoluer dans sa façon de penser ?
Il faut combattre l'obscurantisme !
Je pense que tu aurais beaucoup à lui apporter

Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Rønin47 a écrit:
Hobb n'a pas lu l'oeuvre de Wolinsky, d'où sa réaction réfractaire...
Pourquoi ne pas l'amener à évoluer dans sa façon de penser ?
Pas besoin;; Ayant fait es efforts nécessaire pour essayer de comprendre tout ça, je trouve déplacé que quelqu'un ne les ayant pas fait nous targue de son incompréhension pour nous expliquer comment on doit faire. Qu'il le fasse, on verra ensuite.
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
J'avoue être perdu... Vous êtes scientifique et des personnes sur ce forum détiennent des vérités grâce à la psychologie quantique... Cela devrait vous aider pour mieux comprendre votre domaine, non ? Peut-être que vous êtes trop dans le mental ? Stephen Wolinsky a un cursus d’hypnothérapeute, avez-vous essayé cette méthode avant de juger ? Il est vrai que je ne suis pas très calé, mais Alexandre vous en parlerait bien mieux que moi !hobb a écrit:Rønin47 a écrit:
Hobb n'a pas lu l'oeuvre de Wolinsky, d'où sa réaction réfractaire...
Pourquoi ne pas l'amener à évoluer dans sa façon de penser ?
Pas besoin;; Ayant fait es efforts nécessaire pour essayer de comprendre tout ça, je trouve déplacé que quelqu'un ne les ayant pas fait nous targue de son incompréhension pour nous expliquer comment on doit faire. Qu'il le fasse, on verra ensuite.
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
@hobb :  désolé pour les intrusions dans ce fil. J'ai tiqué dès les premiers messages et j'hésitais sur la sincérité de l'intervenant mais maintenant je n'ai plus de doute...
désolé pour les intrusions dans ce fil. J'ai tiqué dès les premiers messages et j'hésitais sur la sincérité de l'intervenant mais maintenant je n'ai plus de doute...
Il faut plus de finesse et de talent pour le pastiche ou la caricature. N'est pas clo(w) n(e) qui veut...
 désolé pour les intrusions dans ce fil. J'ai tiqué dès les premiers messages et j'hésitais sur la sincérité de l'intervenant mais maintenant je n'ai plus de doute...
désolé pour les intrusions dans ce fil. J'ai tiqué dès les premiers messages et j'hésitais sur la sincérité de l'intervenant mais maintenant je n'ai plus de doute...Il faut plus de finesse et de talent pour le pastiche ou la caricature. N'est pas clo(w) n(e) qui veut...
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
.
Dernière édition par ortolan le Lun 18 Nov 2019 - 12:35, édité 1 fois

ortolan- Messages : 13579
Date d'inscription : 31/07/2016
Localisation : 404 Not Found
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Rønin47 a écrit: des personnes sur ce forum détiennent des vérités

Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
ortolan a écrit:Ah ?J'avais capté au premier message ; peut-être un "délit d'initié" à avoir lu ses interventions antérieures. Mais je conçois ce que la flatterie peut avoir comme effet délétère sur nos capacités de perception et de jugement.
Ou plus simplement le fait d'avoir reçu à plusieurs reprises des mails de "nouveaux venus" du même genre mais qui eux étaient sincères
Et sinon, effectivement je ne passe plus mon temps à lire l'intégralité de ZC chaque jour...
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Salut Alexandre,
toute la subtilité des smileys...
Alexandre a écrit:@hobb :désolé pour les intrusions dans ce fil. J'ai tiqué dès les premiers messages et j'hésitais sur la sincérité de l'intervenant mais maintenant je n'ai plus de doute...
Il faut plus de finesse et de talent pour le pastiche ou la caricature. N'est pas clo(w) n(e) qui veut...
toute la subtilité des smileys...
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
.
Dernière édition par ZebMckay11 le Mer 18 Juil 2018 - 20:07, édité 1 fois
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Zeb : Je ne sais pas si je te suis bien, mais je me suis déjà dit que la problematique venait peut-être du fait que l'on étudiait indépendament sans prendre en compte l'environnement (comme tu souligne la vitesse de rotation de la terre par ex), selon telle température, tels matériaux utilisés ou même des choses encore plus subtiles comme les fonctions organiques qui entourent.
Je ne crois pas à ce total hasard. Je pense que si une chose va a gauche plutôt qu'a droite c'est que quelque chose l'a poussé a gauche plutôt qu'a droite. Et cela vient non pas seulement d'un environnement exterieur, que interieur, comme une sorte de dialectique.
Après on m'a parlé d'autre façon aussi de voir le choses, considerant non pas le reel "subjectif" et aléatoire, mais comme notre propre regard le serait avant tout. Ce qui ne déterminerait donc pas la chose elle-même comme subjective et aléatoire, mais comme manque de connaissance.
Je n'y connais absolument rien, je ne sais pas un jour si je m'y plongerais(dans les maths et physique "pure"). Comme tu le dis, chacun son truc. Mais ça ne m'empeche pas d'aimer penser à ces choses, de "visualiser" ou de mettre en perspective avec d'autres "modèles".
Je ne crois pas à ce total hasard. Je pense que si une chose va a gauche plutôt qu'a droite c'est que quelque chose l'a poussé a gauche plutôt qu'a droite. Et cela vient non pas seulement d'un environnement exterieur, que interieur, comme une sorte de dialectique.
Après on m'a parlé d'autre façon aussi de voir le choses, considerant non pas le reel "subjectif" et aléatoire, mais comme notre propre regard le serait avant tout. Ce qui ne déterminerait donc pas la chose elle-même comme subjective et aléatoire, mais comme manque de connaissance.
Je n'y connais absolument rien, je ne sais pas un jour si je m'y plongerais(dans les maths et physique "pure"). Comme tu le dis, chacun son truc. Mais ça ne m'empeche pas d'aimer penser à ces choses, de "visualiser" ou de mettre en perspective avec d'autres "modèles".
Like a Frog- Messages : 1151
Date d'inscription : 24/05/2018
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
.
Dernière édition par ZebMckay11 le Mer 18 Juil 2018 - 20:07, édité 1 fois
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Tu viens de m'apprendre deux mots !
Si tu as d'autres liens (en francais) je suis preneuse. (j'ai quelques heures devant moi)
@ terra-mumticolor : Merci pour ce que tu as dis, je t'avais déjà "observé" sur un autre fil, et quoi que ce soit "vrai ou faux" et que tu ne semble pas finir avec le sophisme et le déni XD, j'apprécie ton espece de volonté.
Et puis merci à tim, je n'ai jamais trop eu l'occasion de bien le lire (cause travail), mais j'espere me plonger dans sa lecture et au moins comprendre deux-trois trucs. (pas gagné d'avance)
Si tu as d'autres liens (en francais) je suis preneuse. (j'ai quelques heures devant moi)
@ terra-mumticolor : Merci pour ce que tu as dis, je t'avais déjà "observé" sur un autre fil, et quoi que ce soit "vrai ou faux" et que tu ne semble pas finir avec le sophisme et le déni XD, j'apprécie ton espece de volonté.
Et puis merci à tim, je n'ai jamais trop eu l'occasion de bien le lire (cause travail), mais j'espere me plonger dans sa lecture et au moins comprendre deux-trois trucs. (pas gagné d'avance)
Like a Frog- Messages : 1151
Date d'inscription : 24/05/2018
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Ce n'est pas sympa de douter de moi...Alexandre a écrit:@hobb :désolé pour les intrusions dans ce fil.
Et je ne vous comprends plus... Reniez-vous ce que vous avez écrit au sujet de la vérité et de la psychologie quantique ? Pourquoi vos propos seraient-ils acceptables en philosophie et non en science, en sachant que toute science découle de la philosophie ? Vous donnez des leçons de morale aux philosophes, vous vous moquez d'eux, et je comprends, n'est pas clown qui veut ! Mais pourquoi s'écraser comme une crêpe devant ceux qui ont pour objet de travail TOUT ce que vous critiquez ? (la raison, le mental)
Il me semble que j'ai bien eu raison de vous dire qu'il fallait avoir plus confiance en vous. Assumez ce que vous dîtes, je l'ai fait à votre place, car je suis d'accord avec vous ! Les scientifiques doivent sortir de l'obscurantisme ! Si cela peut vous rassurer, la philosophie des sciences, c'est l'épistémologie. De grands chercheurs scientifiques comme Etienne Klein sont aussi philosophes, cela les aide dans leur travail. Et s'il est vrai que la psychologie quantique peut nous aider à atteindre la vérité, alors je ne vois pas pourquoi ça n'aiderait pas les scientifiques à mieux comprendre comment fonctionne le monde...
Pourquoi ne leur expliquez-vous pas ce que vous écriviez à d'autres intervenants dans la section philosophie ? Ne perdez pas la confiance cher ami ! Vous avez su montrer à ces philosophes combien ils étaient arrogants et stupides, car ils étaient trop dans le mental, et moi ça m'a éclairé ! Cela m'a vraiment aidé à comprendre que la vérité était la simplicité même, accessible à tous, que même un trisomique 21 pouvait la ressentir dans son coeur, et que ça ne servait à rien de réfléchir !!! N'ai-je pas raison ? Alors pourquoi ne pas aider les chercheurs à abandonner leurs vieux concepts, peut-être qu'ils verraient le monde différemment, non ?
Si vos enseignements sont sérieux, alors expliquez à Hobb et à d'autres la voie qui mènerait à la réussite !
Au nom du bien de tous, vous le devez ! Pour beaucoup, vous êtes comme un maître à présent !
Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Cela est insensé ! Vous êtes bien plus intelligents que moi, et je ne cherche finalement qu'à me mettre à niveau et à aider. Alexandre a compris de grandes choses, notamment sur le bouddhisme, il a saisi ce qu'était la véritable sagesse, et contrairement à beaucoup de personnes, il en a fini avec les jeux de l'ego !ortolan a écrit:Mais je conçois ce que la flatterie peut avoir comme effet délétère sur nos capacités de perception et de jugement.
Comment pourrait-il donc être aussi facilement flatté par un inconnu ?

Invité- Invité
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
.
Dernière édition par ortolan le Lun 18 Nov 2019 - 12:37, édité 1 fois

ortolan- Messages : 13579
Date d'inscription : 31/07/2016
Localisation : 404 Not Found
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
@alexandre : C'est vrai que c'est drôle, mais j'ai trouvé aussi interessant de voir ce que donne une logique poussé dans sa "vérité".
Dommage qu'il n'est pas su se faire plus discret.
Dommage qu'il n'est pas su se faire plus discret.
Like a Frog- Messages : 1151
Date d'inscription : 24/05/2018
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Stephen Wolinsky a un cursus d’hypnothérapeute, avez-vous essayé cette méthode avant de juger ?
C'était drôle, merci quand même pour cette suprise.
Like a Frog- Messages : 1151
Date d'inscription : 24/05/2018
 Re: Physique quantique for dummies
Re: Physique quantique for dummies
Je n'ai pas la même appréciation. J'aurais plutôt dit : "c'était grossier" ! Quand on a des gros sabots, c'est tentant de les garder, c'est tellement confortable... 
Si la modération veut supprimer tous les messages hors sujet (les miens compris), je n'y verrai aucune objection...
Si la modération veut supprimer tous les messages hors sujet (les miens compris), je n'y verrai aucune objection...
Page 7 sur 16 •  1 ... 6, 7, 8 ... 11 ... 16
1 ... 6, 7, 8 ... 11 ... 16 
 Sujets similaires
Sujets similaires» documentaire:intro à la physique quantique...
» Conference interessante physique quantique
» Rayonnement du corps noir, et naissance de la physique quantique...
» ordinateur quantique
» The living matrix (physique quantique, médecine, champ d'information, intuition)
» Conference interessante physique quantique
» Rayonnement du corps noir, et naissance de la physique quantique...
» ordinateur quantique
» The living matrix (physique quantique, médecine, champ d'information, intuition)
Page 7 sur 16
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Évènements
Évènements