Problème de maths à résoudre

x = Q^(1 / Q^(1 / x)) dans R

Différencier* selon les valeurs de Q.

*au sens de différents cas

Je n'ai pas la réponse. À part une : e^(W(ln(Q))) qui est aussi la solution à l'équation x = Q^(1 / x).

W est la fonction W de Lambert.

Cdt.

Sexe

Je vais peut-être dire une connerie.

L'équation s'écrit aussi plus simplement :

x = x^Q/Q pour tout x différent de 0, non ?

Pour Q différent de zéro, tout x appartenant à R (sauf 0) est solution de l'équation.
Pour Q = 0, il n'y a pas de solution.


Non ?

Comment tu arrives à x = x^Q/Q

Damned, je viens de me rendre compte que j'ai mal interprêté le "^". Je l'ai considéré comme un signe "multiplier" au lieu de le prendre comme une puissance .

Ouais faut pas confondre ^^

Bon, si je ne me suis pas gouré cette fois, on peut ré-écrire l'expression initiale sous la forme :

ln(x) / x = ln(Q) / Q pour tout Q>0

En prenant le log népérien des deux termes, puis en simplifiant l'écriture à grands coups de ln (a^b) = a.ln(b).

Du coup, une des solutions est x=Q pour tout Q strictement positif.
Pour Q=0, il ne peut y avoir de solution.

Même raisonnement avec Q négatif, on obtient :
ln(-x) = ln(-Q)/Q
Solution identique : x=Q pour tout Q strictement négatif.

LA grande question qui reste à répondre est : existe-t-il d'autres solutions ?

Non ?

Je crois pas

x = Q^(1 / Q^(1 / x))

x = e^((1 / Q^(1 / x)) ln(Q))

ln(x) = (1 / Q^(1 / x)) ln(Q)
ln(Q) / ln(x) = Q^(1 / x)
ln(Q) / ln(x) = e^((1 / x) ln(Q))
ln(ln(Q) / ln(x)) = ln(Q) / x

On peut simplifier l'écriture en mettant ln(x) / ln(Q) = logQ(x) [log à base Q de x]

1 / logQ(1 / logQ(x)) = x

Pas sûr que les deux expressions soient incompatibles, si ?

j'essaie de détailler comment j'arrive à ln(x)/x =ln(Q)/Q.

x = Q^(1/Q^(1/x))

Je prends le log népérien de chaque expression : ln(x) = ln(Q^(1/Q^(1/x)))

Je sors la puissance du log népérien : ln(x) = (1/Q^(1/x)).ln(Q)

Je passe la fraction de l'autre côté : (Q^(1/x)).ln(x) = ln(Q)

J'intègre la fraction dans le log népérien comme une puissance de x : ln(x^(Q ^(1/x))) = ln(Q)

Je sors la fraction 1/x du log népérien : (1/x).ln(x^Q) = ln(Q)

Je sors le Q du log népérien : (Q/x).ln(x) = ln(Q)

Je passe le Q de l'autre côté : ln(x) / x = ln(Q) / Q



(si j'ai faux, je veux bien l'explication, ça fait une éternité que je n'ai plus manipulé des logarithmes).

x^(Q ^(1/x)) ≠ (x^Q)^(1 x)

Ex.

2^(3^2) = 2^9 = 512
(2^3)^2 = 8^2 = 64

Ach c'est l'horreur à lire en linéaire comme ça.
Tu aurais l'expression initiale écrite "à la main" ?

I faut d'mander l'install d'un plugin maths

Siouplait la modération, vous qui m'aimez tellement, z'auriez pas l'extrême obligeance d'installer un plugin maths ?

Merci tout simplement

Il faut que je fasse un petit laïus sur la fonction W de Lambert

La fonction W de Lambert est l'inverse de la fonction

xe^x

Qui permet de résoudre des équations où y'a des x et des e^x

Je vais juste paraphraser un peu ça https://fr.m.wikipedia.org/wiki/Fonction_W_de_Lambert

Donc pour l'équation x = Q^(1 / x)

Qui est en fait une autre écriture de l'équation x^x = Q

Cette équation se résoud en faisant apparaître un terme A(x)e^A(x)

Si A(x)e^A(x) = y

W(y) = A(x)

e^(x * ln(x)) = Q

x * ln(x) = ln(Q)

W(x * ln(x)) = ln(x)

[propriété]

Donc ça supprime le facteur x

ln(x) = W(ln(Q))

x = e^(W(ln(Q)))

Donc c'est la solution de l'équation x = Q^(1 / x) mais pas l'équation du début bien sûr

Deux choses à noter

Pour - 1 / e < ln(Q) < 0 il y a deux solutions

Puisque la fonction W de Lambert a deux branches sur cet interval (cf. Wikipedia)

Pour ln(Q) < - 1 / e il n'y a pas de solution dans R

Pour ln(Q) >= 0 il y a une solution dans R

La deuxième chose à noter est que le site https://www.wolframalpha.com/ propose des valeurs numériques pour les deux branches de la fonction W de Lambert

LambertW(x) pour la branche 0 et LambertW(-1, x) pour la branche - 1

Ce site est aussi un site d'intelligence artificielle vous pouvez lui dire

Solve x^x = Q

Il vous répondra



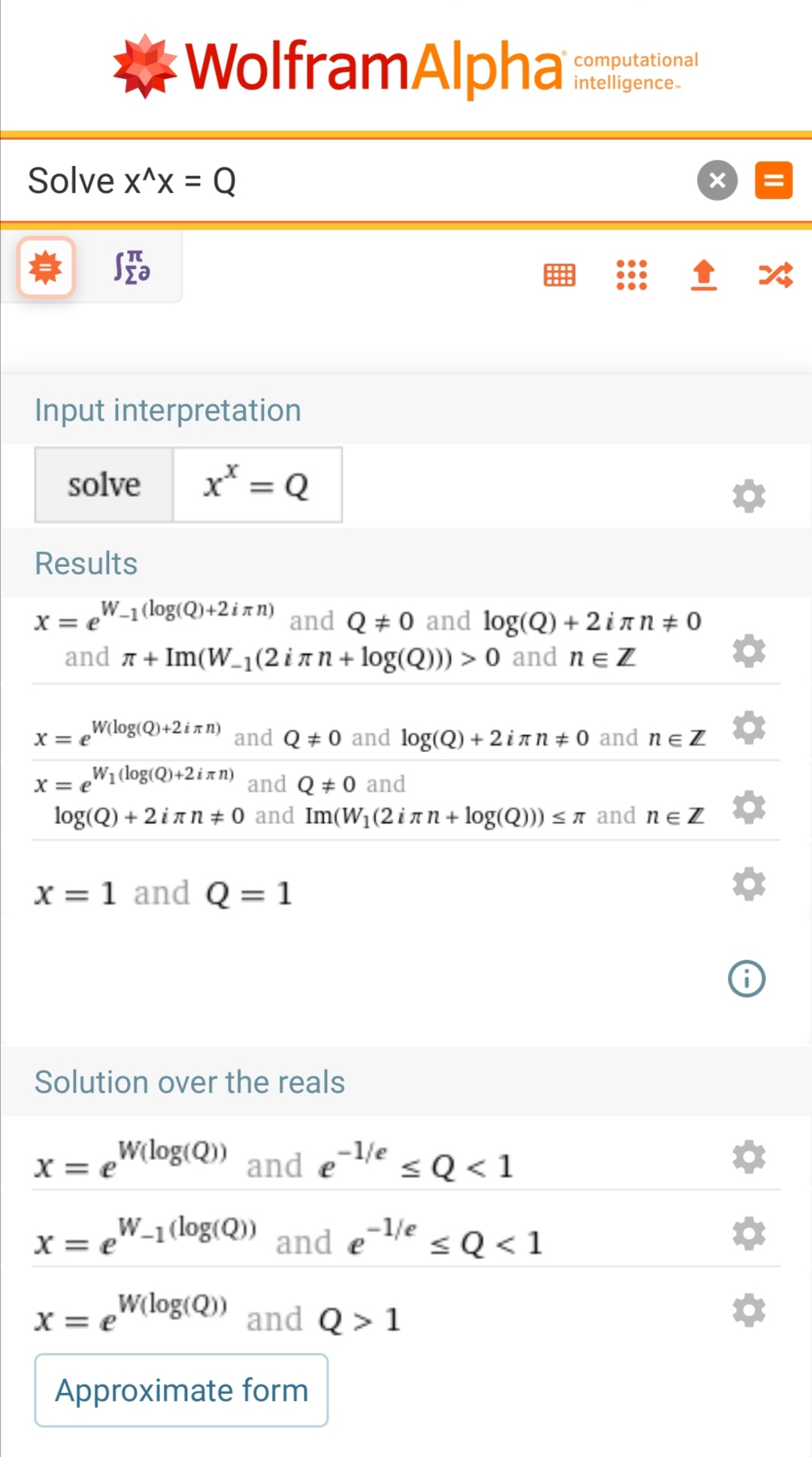
Oui donc j'ai fait une petite erreur c'est ln(Q) >= - 1 / e et non ln(Q) > - 1 / e

Vous pouvez lui dire

What is the capital of France

Il vous répondra



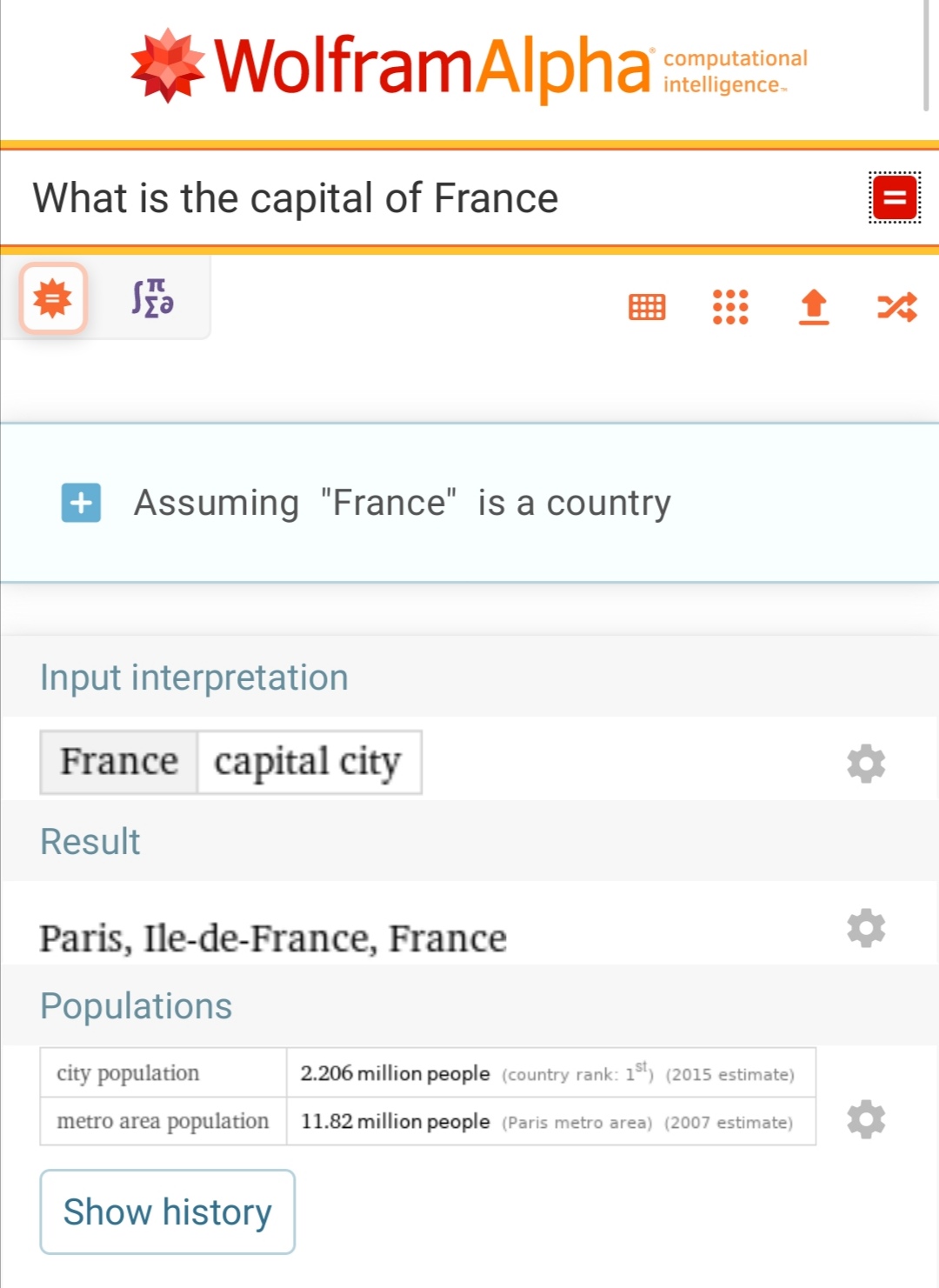
Notez que les raisonnements sont indiqués

Et donc bien sûr vous allez vous précipiter pour lui dire

Solve x = Q^(1 / Q^(1 / x))

Qui est je vous l'rappelle le but de ce fil

Et il vous répondra malheureusement



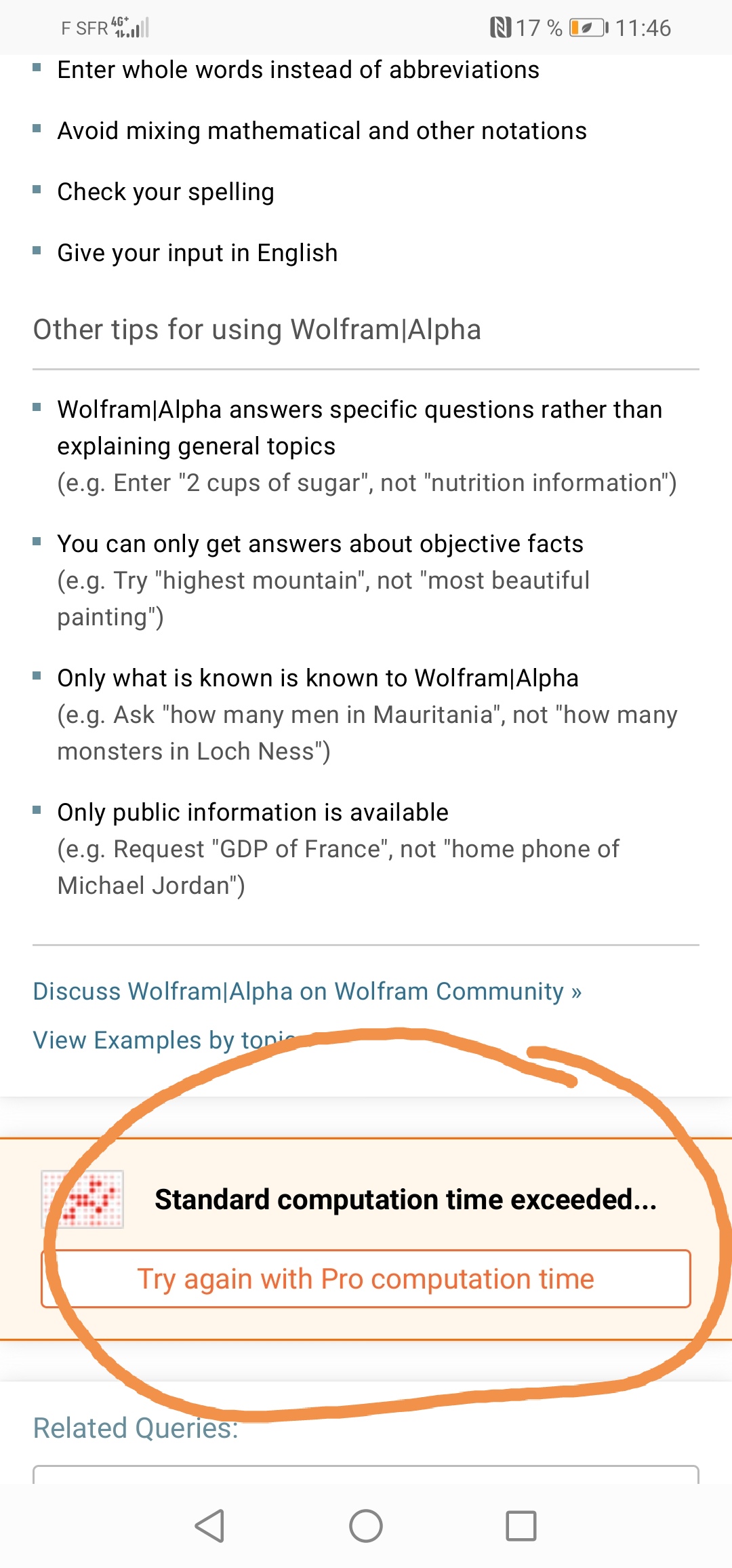
Si quelqu'un veut essayer le pro computation time je l'en prie

Peace.

fift a écrit:Ach c'est l'horreur à lire en linéaire comme ça.
Tu aurais l'expression initiale écrite "à la main" ?

Ce n'est pas vraiment l'horreur c'est juste submergeant.

Refresh

[edit pour préciser mon pseudo était sexe à l'époque d'où le sexe en fin de premier message have a nice evening]

J'ai payé l'abonnement pro à wolframalpha mais il n'a pas su résoudre non plus apparemment

Bof

x = Q^(1 / Q^(1 / x))
ln(x) = (1 / Q^(1 / x)) ln(Q)
Ok

ln(x) / ln(Q) = 1 / Q^(1 / x)
ln(Q) = ln(x) * Q^(1 / x)
ln(Q) / ln(x) = Q^(1 / x)
ln(ln(Q) / ln(x)) = 1 / x * ln(Q)

Donc effectivement

ln(Q) = x * ln(ln(Q) / ln(x))

Comment tu arrives à

[ ln(ln(x)) - ln(ln(Q)) ] exp [ ln(ln(x)) - ln(ln(Q)) ] = - ln(x) / x

On peut en tout cas simplifier l'écriture en utilisant logq(x) = ln(x) / ln(Q)

logq(logq(x)) = 1 / x

Enfin non

logq(1 / logq(x)) = 1 / x

ln(Q) = x * ln(ln(Q) / ln(x))
Q = (ln(Q) / ln(x))^x

.

(- ln(Q) / x) * (ln(x) - ln(Q)) = ?

Alors je te fais toujours de la peine ?

Tu m'avais dit que je te faisais de la peine

Ouais, bon, comment tu exprimes x en fonction de Q

Cuba libre a écrit:Ouais, bon, comment tu exprimes x en fonction de Q

Par une fonction analytique je ne sais pas faire.

Combien de solutions en fonction de Q

Numériquement ça a pas l'air de super coller

ln(ln(x)) - ln(ln(Q)) = - ln(x)
ln(ln(x)) + ln(x) = ln(ln(Q))
ln(x) * x = ln(Q)

Donc on retrouve la solution ci-dessus qui est x = e^(W(ln(Q)))

Je pense que pour certaines valeurs de Q il y a trois solutions, d'après desmos.com et le tracé des courbes y = x et y = Q^(1 / Q^(1 / x))

Comme l'équation ln(Q) = x / ln(x) n'a pas de solution analytique (d'après Câlin) je propose cette équation comme un problème parallèle, puisque l'on ne se trompe pas par hasard.

Q est fixe et il faut trouver x en fonction de Q et non l'inverse

Q = x^x n'est pas une solution

x = e^(W(ln(Q))) est une solution

Q < 1 donne deux valeurs de x

ln(Q) < - 1 / e soit Q < e^(- 1 / e) donne zéro solution

En attendant je propose de travailler sur l'équation ln(Q) = x / ln(x)

Que l'on peut écrire q = x / ln(x)

Apparemment vu sur https://fr.quora.com/Comment-r%C3%A9soudre-ln-x-ax-a-r%C3%A9el il existe une solution avec la fonction W de Lambert

ln(x) * q = x
ln(x) = x / q
x = e^(x / q)
xe^(- x / q) = 1
- (x / q)e^(- x / q) = - 1 / q
W(- (x / q)e^(- x / q)) = W(- 1 / q)
- x / q = W(- 1 / q)
x = - q * W(-1 / q)

- 1 / q appartient [- 1 / e ; +oo[ donc 1 / q appartient à ] -oo ; 1 / e] et q appartient à ] -oo ; e]

Q appartient à [0 ; e^e]

Non j'ai peut-être fait une erreur sur la valeur de petit q

q appartient à ] -oo ; 0] U [e ; +oo[

En fait 0 est exclus

Ou pas

Disons que la limite de x / ln(x) en 0 vaut 0

Il est peut-être possible d'utiliser la méthode de câlin en "faisant gaffe" aux intervalles pour expliciter les autres solutions

câlin a écrit:

Pourquoi tu voulais savoir en fait ? ^^

Pourquoi tu as répondu ?

câlin a écrit:

J'ai trouvé une solution exprimée en fonction de la fonction W de Lambert. Je trouve

W(- ln(x) / x) = ln(ln(x)) - ln(ln(Q))

Démo :

ln(Q) = x [ ln(ln(Q)) - ln(ln(x)) ]

[ ln(ln(x)) - ln(ln(Q)) ] exp [ ln(ln(x)) - ln(ln(Q)) ] = - ln(x) / x

Y exp(Y) = X

avec Y = ln(ln(x)) - ln(ln(Q))
       X = - ln(x) / x

donc W(X) = Y  CQFD

Et la page Wikipedia nous renseigne sur quelques valeurs particulières :

W(0) = 0 est un cas pathologique mais correspond trivialement à x = 1 et Q = 1
W(-1/e)  = -1 correspond à x = e et Q = e^e

Et au miracle le Wikipedia nous dit que W(-ln(x) / x) = - ln(x). C'est exactement ce qu'on a, la solution est analytique !

Y = -ln(x)
ln(ln(Q)) = ln(x) + ln(ln(x))

Q = exp(x*ln(x))

Q = x^x

On retrouve bien la solution triviale donnée au début du fil. Et pour l'autre solution qui existe parfois, elle est donnée par l'autre branche de la fonction W de lambert (elle existe pour x > 1) :

ln(ln(Q)) = ln(ln(x)) - W(-ln(x) / x)

Pourquoi tu voulais savoir en fait ? ^^

Le déroulé me semble intéressant mais tout cela se démontre en deux lignes

Si x^x = Q

Alors x = Q^(1 / x) pour x ≠ 0

On remplace x dans la partie droite :

x = Q^(1 / (Q^(1 / x))