La physique en questions (de Jean-Marc Lévy-Leblond)
+7
câlin
Charv
RonaldMcDonald
isadora
persntm 2
Laelia
Topsy Turvy
11 participants
Page 1 sur 4
Page 1 sur 4 • 1, 2, 3, 4 
 La physique en questions (de Jean-Marc Lévy-Leblond)
La physique en questions (de Jean-Marc Lévy-Leblond)
Dans les gens que j'aime bien, il y a, entre autres, Jean-Marc Lévy-Leblond.
il a enseigné dans les départements de physique, de philosophie et de communication
https://fr.wikipedia.org/wiki/Jean-Marc_Lévy-Leblond
Il a publié des trucs sympas, dont cette paire d'ouvrages, malheureusement plus édités :
La Physique en questions, exercices de physique générale, en 2 tomes : 1. Mécanique, 2. Électricité et magnétisme (Vuibert)
En apéritif, je propose la question qui figure dans le texte de présentation du tome 1.
Les savants et les joueurs sont invités à répondre de tête ou en spoiler, pour ne pas gâcher.

il a enseigné dans les départements de physique, de philosophie et de communication
https://fr.wikipedia.org/wiki/Jean-Marc_Lévy-Leblond
Il a publié des trucs sympas, dont cette paire d'ouvrages, malheureusement plus édités :
La Physique en questions, exercices de physique générale, en 2 tomes : 1. Mécanique, 2. Électricité et magnétisme (Vuibert)
En apéritif, je propose la question qui figure dans le texte de présentation du tome 1.
Les savants et les joueurs sont invités à répondre de tête ou en spoiler, pour ne pas gâcher.
Une corde passe par-dessus une poulie en pendant symétriquement de chaque côté. A l'une des extrémités est agrippé un singe et à l'autre, on a suspendu un miroir de même poids que lui. Effrayé par son image, le singe tente d'y échapper en grimpant le long de la corde. Que se passe-t-il alors ?


Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Je propose une variante de la donnée pour peut-être faciliter la représentation de la situation et de son évolution. Disons qu'au départ il y a un couple de vrai jumeaux, chacun agrippé à une extrémité d'une corde, soutenue en son milieu par une poulie. On imagine tout assez grand pour éviter que l'un et l'autre soient en contact, pour qu'il y ait bien la possibilité d'observer un effet, etc. L'un des deux ne fait rien d'autre que de rester agrippé. L'autre se met en tête de faire, pour sa part, un entrainement de grimper à la corde. Il s'active, tend les bras, saisit la corde, tire, bloque avec les jambes, recommence, etc. Que se passe-t-il alors ?

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
- Spoiler:
- Un seul bouge, les deux montent.
Laelia- Messages : 2911
Date d'inscription : 23/02/2022
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Ah ouais, c'est compliqué ! (ou pas, mais, là tout de suite, ça ressemble â une énigme...Topsy Turvy a écrit:Je propose une variante de la donnée pour peut-être faciliter la représentation de la situation et de son évolution. Disons qu'au départ il y a un couple de vrai jumeaux, chacun agrippé à une extrémité d'une corde, soutenue en son milieu par une poulie. On imagine tout assez grand pour éviter que l'un et l'autre soient en contact, pour qu'il y ait bien la possibilité d'observer un effet, etc. L'un des deux ne fait rien d'autre que de rester agrippé. L'autre se met en tête de faire, pour sa part, un entrainement de grimper à la corde. Il s'active, tend les bras, saisit la corde, tire, bloque avec les jambes, recommence, etc. Que se passe-t-il alors ?
- Réflexion en spoiler, ne pas lire pour ne pas être enduit d'erreur:
- Déjà, c'est logique de se dire que si aucun des deux ne bouge, le système reste à l'équilibre... Je commence par me dire ça même si ça semble ultra évident et que c'est la situation de départ.
Le problème, quand l'un des deux grimpe, c'est qu'il évolue le long de la corde et qu'il se rapproche de la position du deuxième sur cette corde : c'est comme si la situation de départ était encore la même (un singe de chaque côté de la poulie à la même hauteur par rapport au sol et à la même distance de la poulie), mais le bout de corde qui les sépare diminue en taille, donc j'imagine qu'à un moment le singe qui grimpe n'aura plus de corde à grimper : son bout de corde juste au-dessus de lui va être quasi nul par rapport à l'emplacement de la poulie.
Celui qui a grimpé accumule plus de corde de son côté, donc le poids n'est plus à l'équilibre, sauf si la corde est très longue et qu'elle repose par terre sur un sol qui est au même niveau des deux côtés. S'il y a plus de corde qui pend dans le vide du côté du grimpeur, bah, j'imagine qu'on s'en fout car cette quantité de corde en plus doit avoir un poids négligeable par rapports aux dizaines de kilos qui sont réparties (les singes) de chaque côté.
Si on reprend l'énoncé du premier message, il faut ajouter le fait que le singe qui grimpe se demande s'il est vraiment un singe tout en grimpant.

persntm 2- Messages : 633
Date d'inscription : 28/04/2023
Localisation : exerce ses doudounes d'homme
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Une autre très accessible pour se mettre en forme, je repasserai avec les développements de chacune si nécessaire ou désiré, l'idée est bien de s'amuser sur de vraies questions qui peuvent paraître évidentes ou laisser songeur.
Pourquoi le sel est-il soluble dans l'eau et pas dans l'huile ?

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
- huile sel:
- De mémoire lointaine, l'eau est une molécule polaire, du coup plus réactive que les huiles. Le sel se dissout dans l'eau parce que la molécule se défait en Na+ et Cl- qui interagissent avec l'eau.
Dans les molécules lipidiques, c'est pas polaire, par contre la fonction COOH peut perdre un H (ce qui ne doit probablement pas arriver dans une huile où ya que ça comme molécule ?)
La chimie, c'est loin...........
Laelia- Messages : 2911
Date d'inscription : 23/02/2022
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
est ce que sans réflexion scientifique ou connaissances en chimie on peut répondre naivement : parce que l huile et l eau ne se mélangent pas ?
isadora- Messages : 3889
Date d'inscription : 04/09/2011
Localisation : Lyon
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Tout le monde peut répondre, avec grand plaisir.
On ne s'intéresse pas ici à qui sait quoi, ni qui serait plus juste ou moins juste. Je ne vais proposer que quelques-unes des questions qui peuvent me paraître éventuellement amusantes, intrigantes, étonnantes, bizarres,... Il n'y a pas de volonté de piéger, ni d'évaluer des connaissances. L'idée est de jouer, éventuellement en se grattant la tête, mais sans s'arracher les cheveux. Pour une idée de ce qui anime Lévy-Leblond :
https://pubs.aip.org/aapt/ajp/article/47/11/928/1050983/James-Clerk-Maxwell-s-inaugural-lecture-at-King-s
Pour le singe et le miroir, il est vrai qu'en agrandissant les éléments pour bien visualiser j'ai amené à considérer le poids de la corde. Alors on va rectifier la longueur de la corde pour qu'on ait toujours le même poids de corde de part et d'autre (pour la poulie). Singe ou miroir ou jumeaux sont donc accrochés, par exemple à deux mètre du sol dans une salle de gymnastique, à une corde très longue dont les extrémités reposent au sol, avec beaucoup de marge de part et d'autre.
parce que l huile et l eau ne se mélangent pas
Ce qui est juste mais qui m'amène à demander pourquoi ils ne se mélangent pas, l'un et l'autre effet découlant de la même cause. Ce à quoi on est encore libre de proposer des réponses plus ou moins naïves ou expertes, pour autant qu'on y ait du plaisir à s'étonner, s'émerveiller,...
On ne s'intéresse pas ici à qui sait quoi, ni qui serait plus juste ou moins juste. Je ne vais proposer que quelques-unes des questions qui peuvent me paraître éventuellement amusantes, intrigantes, étonnantes, bizarres,... Il n'y a pas de volonté de piéger, ni d'évaluer des connaissances. L'idée est de jouer, éventuellement en se grattant la tête, mais sans s'arracher les cheveux. Pour une idée de ce qui anime Lévy-Leblond :
Toujours pour donner une idée de ce qui anime Lévy-Leblond, deux des trois citations qui ouvrent le second tome :...« (re)mettre la science en culture ». « Depuis longtemps, Jean-Marc Lévy-Leblond tire la sonnette d’alarme sur la nécessité d’une intelligence publique des sciences, où se noueraient savoirs, recherche, culture et politique [...]. Afin de préserver d’authentiques discours scientifiques et éviter un fossé d’incompréhension entre les spécialistes et le grand public, mais aussi cultiver la nécessité d’une histoire des sciences, contre l’illusion d’une universalité de la connaissance scientifique, contre le présentisme et les phantasmes de contemporanéité absolue, contre la soumission des sciences aux impératifs industriels, contre l’uniformisation planétaire qu’installe la domination des technosciences ». ...
https://fr.wikipedia.org/wiki/Jean-Marc_Lévy-Leblond
Si l'on plonge un illettré total et une marchande de gaufres dans un bain de yaourt et qu'on les réunit par un fil de cuivre de diamètre convenable, on obtient un courant électrique tellement faible qu'il ne peut servir à rien.
Cavanna, Le saviez-vous ? (Petite encyclopédie portative pour consoler les bons-à-rien.) (Éditions du Square, Paris, 1979).
Parce que j'ai le vilain défaut de creuser quand un truc m'intéresse, le texte de la leçon inaugurale de Maxwell est accessible en PDF par là, en anglais :Je connais la tendance de l'esprit humain à faire n'importe quoi plutôt que de penser. Certes, aucun d’entre nous n’espère réussir sans travail. Nous savons tous qu'acquérir un tant soit peu de science exige un effort intellectuel considérable, et je suis sûr que nous y sommes prêts pour avancer dans notre disci pline. Mais effort intellectuel n'égale pas pensée. Et ceux qui, à grand'peine, ont acquis l'habitude de s'appliquer à leur tâche, souvent trouvent plus aisé d'apprendre une formule que de maîtriser un principe. Je m'efforcerai ici de vous montrer, et vous le vérifierez plus tard, que les principes sont fertiles en résultats, alors que les résultats seuls sont stériles. Celui qui a appris une formule est à la merci de sa mémoire, mais celui qui a maîtrisé un principe peut garder son esprit libre de formules, sachant qu'il peut en fabriquer autant que nécessaire, le moment voulu. Dois-je ajouter que, malgré le recul naturel de l'esprit devant le dur processus de la pensée, pourtant, ce processus une fois accompli, l'esprit ressent une puissance et une jouissance que l'amènent à mépriser désormais les peines et angoisses qui accompagnent son passage d'un stade de développement à un autre ?
James C. Maxwell, Conférence inaugurale au King's College de Londres (1860) (texte original reproduit dans Am. J. Phys. 47, 928 (1979)].
https://pubs.aip.org/aapt/ajp/article/47/11/928/1050983/James-Clerk-Maxwell-s-inaugural-lecture-at-King-s
Pour le singe et le miroir, il est vrai qu'en agrandissant les éléments pour bien visualiser j'ai amené à considérer le poids de la corde. Alors on va rectifier la longueur de la corde pour qu'on ait toujours le même poids de corde de part et d'autre (pour la poulie). Singe ou miroir ou jumeaux sont donc accrochés, par exemple à deux mètre du sol dans une salle de gymnastique, à une corde très longue dont les extrémités reposent au sol, avec beaucoup de marge de part et d'autre.
parce que l huile et l eau ne se mélangent pas
Ce qui est juste mais qui m'amène à demander pourquoi ils ne se mélangent pas, l'un et l'autre effet découlant de la même cause. Ce à quoi on est encore libre de proposer des réponses plus ou moins naïves ou expertes, pour autant qu'on y ait du plaisir à s'étonner, s'émerveiller,...

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
...
Dernière édition par Largo le Dim 21 Mai 2023 - 8:26, édité 1 fois
Invité- Invité
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Si tu trouves les textes de l'époque qui en parlent cela m'intéresse
Le Treatise on electricity and magnetism de Maxwell (1873) est consultable en pdf de livre numérisé, par exemple là le premier volume :
https://www.aproged.pt/biblioteca/MaxwellI.pdf
ou en format texte, par exemple sur wikisource :
https://en.wikisource.org/wiki/A_Treatise_on_Electricity_and_Magnetism
Les trois volumes de travaux de Maxwell aux archives du King's College ne sont pas numérisés.

Le Treatise on electricity and magnetism de Maxwell (1873) est consultable en pdf de livre numérisé, par exemple là le premier volume :
https://www.aproged.pt/biblioteca/MaxwellI.pdf
ou en format texte, par exemple sur wikisource :
https://en.wikisource.org/wiki/A_Treatise_on_Electricity_and_Magnetism
Les trois volumes de travaux de Maxwell aux archives du King's College ne sont pas numérisés.
Delphine et Marinette veulent se partager à parts égales le gros sucre d'orge ("candy cane") que l'oncle Alfred leur a acheté à la foire. Delphine propose de le suspendre par un fil, de trouver la position d'équilibre et de couper la canne au point d'attache ainsi déterminé.
Les deux parties ainsi obtenues ont-elles le même poids ? Sinon, lequel est le plus lourd ?


Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
...
Dernière édition par Largo le Dim 21 Mai 2023 - 8:26, édité 1 fois
Invité- Invité
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Topsy Turvy a écrit:Delphine et Marinette veulent se partager à parts égales le gros sucre d'orge ("candy cane") que l'oncle Alfred leur a acheté à la foire. Delphine propose de le suspendre par un fil, de trouver la position d'équilibre et de couper la canne au point d'attache ainsi déterminé.
Les deux parties ainsi obtenues ont-elles le même poids ? Sinon, lequel est le plus lourd ?
- Réponse:
- Elles le font fondre dans une casserole, puis à l'aide d'une éprouvette graduée, elles transfèrent la moitié du liquide obtenu dans un moule deux fois plus petit que la confiserie d'origine. Elles obtiennent deux confiseries de même poids une fois que ça a redurci, puis elles arrêtent de nous embêter. (sales gosses...)

persntm 2- Messages : 633
Date d'inscription : 28/04/2023
Localisation : exerce ses doudounes d'homme
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
On continue...
Une autre :
- Réponse du livre à la question du singe apeuré par son reflet :
- La tension de la corde est la même en tout point. Le miroir est donc soumis à la même force que le singe et subit la même accélération. Comme les conditions initiales sont identiques (vitesses nulles, hauteurs égales) les mouvements [au sens de déplacements dans l'espace] sont identiques. Le miroir monte donc à la même vitesse que le singe, qui ne peut échapper à son image, si frénétique qu'il monte !
Je précise qu passage que j'ai retrouvé les deux ouvrages en question en pdf en ligne, mais en espagnol pour le tome 1. Les motivés peuvent fouiller pour mettre la main sur l'un et/ou l'autre tome. Si quelqu'un trouve le 1 en français, ça m'intéresse. Pour l'instant, je me contente de balancer les questions de mécanique en traduction automatique. Il s'agit donc bien des contenus de Lévy-Leblond, à moins que je comment ou complète, comme par exemple ci-dessus entre crochets. Mais il se pourrait que la traduction en aller et retour (F-E-F) ne corresponde pas exactement à la version originale. Je veille juste à ce que le fonds ne soit pas affecté par des détails liés à la forme.
Une autre :
a) Si l'on charge électriquement une bulle de savon, son diamètre va-t-il augmenter, diminuer ou rester le même ?
b) Si l'on place une bulle de savon dans un champ électrique uniforme, que devient sa forme ?

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Delphine et Marinette...
je ne fonctionne qu'à l'intuition.
je me méfierais de la méthode telle quelle, je couperais la partie courbe pour obtenir un fer à cheval que je couperais en deux et je couperais en deux l'autre morceau. on peut se servir d'un fil qui équilibre les poids ou ...
pour couper en deux, je ferais comme j'avais instauré dans ma famille : "je coupe, tu choisis. "
la meilleure assurance que deux personnes soient servies à leur convenance pour un partage en deux. qui est quand même ce qu'on recherche dans cette histoire, non ?
je ne fonctionne qu'à l'intuition.
je me méfierais de la méthode telle quelle, je couperais la partie courbe pour obtenir un fer à cheval que je couperais en deux et je couperais en deux l'autre morceau. on peut se servir d'un fil qui équilibre les poids ou ...
pour couper en deux, je ferais comme j'avais instauré dans ma famille : "je coupe, tu choisis. "
la meilleure assurance que deux personnes soient servies à leur convenance pour un partage en deux. qui est quand même ce qu'on recherche dans cette histoire, non ?
isadora- Messages : 3889
Date d'inscription : 04/09/2011
Localisation : Lyon
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Non mais toi, isadora, ça ne compte pas, tu penses à tout.


- Réponse du livre pour le partage de Delphine et Marinette :
- Pour qu'il y ait équilibre, il faut que soient égaux, non pas les poids, mais leurs moments. Le plus petit bras de levier correspondra donc au plus grand poids. La partie avec le manche de la canne en bonbon sera la plus lourde.
Une expérience similaire peut facilement être réalisée : tenir un balai horizontalement sur les index tendus des deux mains écartées, puis rapprochez vos mains; les deux doigts se rejoindront au centre de gravité (...), plus proche de la tête du balai. Si le manche est scié à ce point d'équilibre, il est facile de voir que la tête est plus lourde et plus courte.
Oui, bon, l'expérience demande du matériel, mais ce n'est pas comme si ça coûtait un balai. Enfin...

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Je ne trouve pas que la réponse soit compréhensible par des non physiciens. C'est ultra synthétique, et même à la fois technique et du genre pas clair.Topsy Turvy a écrit:On continue...
- Réponse du livre à la question du singe apeuré par son reflet :

persntm 2- Messages : 633
Date d'inscription : 28/04/2023
Localisation : exerce ses doudounes d'homme
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
- Spoiler:
- Le sucre d’orge : je me doutais qu’il y’avait au final une histoire de poids au bout des extrémités, par contre impossible de déduire qui serait le plus lourd et j’ai toujours pas compris pourquoi.
Pour ce qui est de l’électricité de la bulle, doit y avoir des histoires de tension de surface qui font tenir la bulle, donc si on fait passer un courant, ça fait bouger les électrons dans un seul sens, du coup la bulle ne tient plus ?
Laelia- Messages : 2911
Date d'inscription : 23/02/2022
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
- Ajout illustration de la situation du candy cane :
- Le quotidien est bourré d'applications du moment de force, l'aptitude d'une force à faire tourner un système, qui dépend de la distance au pivot. C'est par exemple ce sur quoi on s'appuie (ah ah) quand on utilise un pied de biche, mais c'est aussi la raison pour laquelle ça fait du sens d'avoir les poignées de portes à distance des gonds, par exemple.
Pour la bulle de savon, on peut faire quelques expériences à la maison, en la prenant comme partenaire d'interaction de force électrostatique.

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Quelques éléments de réponse à des questions posées ou pas, sur l'eau, le sel, l'huile, etc.
Pourquoi le sel se dissout dans l'eau est pas dans l'huile, pourquoi l'eau et l'huile ne se mélangent pas, pourquoi on utilise du savon pour se laver les mains, pourquoi on peut rater une mayonnaise... tout cela est un peu lié.
On pourrait considérer que l'eau et l'huile ne se mélangent pas parce qu'ils n'ont pas la même densité, la masse volumique de l'huile étant plus basse que celle de l'eau. Mais ces deux liquides ne se mélangent pas non plus en apesanteur, par exemple dans la station spatiale internationale. On ne pourrait pas non plus les faire tenir dans un verre, et les astronautes se lavent les mains sans rincer, en faisant sortir une grosse goutte de savon très dilué d'eau, se frottant les mains avec, puis s'essuyant les mains avec un linge, qui sèche ensuite en cabine avant d'être réutilisé ainsi.
L'eau est une molécule très particulière, parce que c'est un dipôle (comme un petit aimant, même si très faible).
On va dire qu'on parle ici du sel de table, le chlorure de sodium, NaCl, Na+ Cl- sous forme ionique, le sodium cédant un électron au chlore, d'où la charge positive de l'un et négative de l'autre. Le sel de table forme des cristaux cubiques transparents, mais, broyé, les petits cristaux de NaCl en vrac paraissent blancs parce qu'ils dévient la lumière dans toutes les directions, au point de renvoyer toute la lumière blanche reçue.


La nature polaire de l'eau rend compte de diverses particularité de l'eau. C'est un bon solvant pour les ions, donc les sels minéraux, mais ce n'est pas un bon solvant pour les substances apolaires (huiles, graisses, cires,...). On peut dissoudre les substances apolaires, mais avec un solvant apolaire lui aussi, par exemple une tache de graisse avec de la benzine rectifiée.
Mais c'est aussi la nature polaire de l'eau qui fait que les glaçons flottent. Habituellement, la baisse de température (énergie thermique, énergie cinétique des molécules) s'accompagne d'une rétractation de la matière, tandis que la hausse de température implique une dilatation de la matière. Mais l'eau se dilate en passant de l'état liquide à l'état solide (glace), parce qu'alors les molécules d'eau s'organisent en un réseau stable mais relativement espacé, à cause de sa forme et de sa nature polaire.

C'est aussi la nature polaire de l'eau qui fait que cette petite molécule est relativement gourmande en énergie thermique. La même quantité d'énergie thermique fournie à la même masse d'eau et d'huile voit la température de l'eau monter moitié moins vite que la température de l'huile. En miroir, l'eau libère relativement beaucoup d'énergie en refroidissant.
Pour revenir à la question des solvants, on ne peut pas retirer du gras avec de l'eau, sauf si on introduit un troisième type de molécules, amphiphile (=double-amour : une partie est hydrophile (car électriquement chargée), l'autre partie est hydrophobe ('lipophile') parce que non chargée). On en entend plutôt parler sous le nom d'émulsifiants ou de tensioactifs, par exemple.
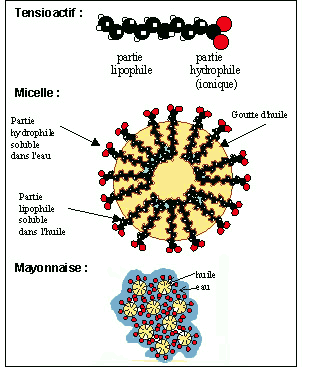
Pourquoi le sel se dissout dans l'eau est pas dans l'huile, pourquoi l'eau et l'huile ne se mélangent pas, pourquoi on utilise du savon pour se laver les mains, pourquoi on peut rater une mayonnaise... tout cela est un peu lié.
- La réponse du livre en spoiler mais je réponds en clair ci-dessous :
- Le sel, comme la plupart des corps ioniques, est soluble dans l'eau car la molécule d'eau est polaire, i.e. forme un dipôle électrique avec un excès de charge négative sur l'oxygène et un excès de charge positive sur les hydrogènes, la molécule restant neutre. Quand les molécules d'eau s'approchent d'un ion (positif ou négatif), elles subissent, comme tout dipôle dans un champ électrique non uniforme, une force attractive vers l'ion, le recouvrant ainsi d'une sorte de coquille qui produit un étalement de sa charge électrique, conduisant à une diminution de son attraction sur les ions de charge opposée. Les ions, accompagnés de leurs molécules d'eau (on dit qu'ils sont hydratés), s'éloignent alors les uns des autres et se dispersent dans l'eau.
On pourrait considérer que l'eau et l'huile ne se mélangent pas parce qu'ils n'ont pas la même densité, la masse volumique de l'huile étant plus basse que celle de l'eau. Mais ces deux liquides ne se mélangent pas non plus en apesanteur, par exemple dans la station spatiale internationale. On ne pourrait pas non plus les faire tenir dans un verre, et les astronautes se lavent les mains sans rincer, en faisant sortir une grosse goutte de savon très dilué d'eau, se frottant les mains avec, puis s'essuyant les mains avec un linge, qui sèche ensuite en cabine avant d'être réutilisé ainsi.
L'eau est une molécule très particulière, parce que c'est un dipôle (comme un petit aimant, même si très faible).
On va dire qu'on parle ici du sel de table, le chlorure de sodium, NaCl, Na+ Cl- sous forme ionique, le sodium cédant un électron au chlore, d'où la charge positive de l'un et négative de l'autre. Le sel de table forme des cristaux cubiques transparents, mais, broyé, les petits cristaux de NaCl en vrac paraissent blancs parce qu'ils dévient la lumière dans toutes les directions, au point de renvoyer toute la lumière blanche reçue.


La nature polaire de l'eau rend compte de diverses particularité de l'eau. C'est un bon solvant pour les ions, donc les sels minéraux, mais ce n'est pas un bon solvant pour les substances apolaires (huiles, graisses, cires,...). On peut dissoudre les substances apolaires, mais avec un solvant apolaire lui aussi, par exemple une tache de graisse avec de la benzine rectifiée.
Mais c'est aussi la nature polaire de l'eau qui fait que les glaçons flottent. Habituellement, la baisse de température (énergie thermique, énergie cinétique des molécules) s'accompagne d'une rétractation de la matière, tandis que la hausse de température implique une dilatation de la matière. Mais l'eau se dilate en passant de l'état liquide à l'état solide (glace), parce qu'alors les molécules d'eau s'organisent en un réseau stable mais relativement espacé, à cause de sa forme et de sa nature polaire.

C'est aussi la nature polaire de l'eau qui fait que cette petite molécule est relativement gourmande en énergie thermique. La même quantité d'énergie thermique fournie à la même masse d'eau et d'huile voit la température de l'eau monter moitié moins vite que la température de l'huile. En miroir, l'eau libère relativement beaucoup d'énergie en refroidissant.
Pour revenir à la question des solvants, on ne peut pas retirer du gras avec de l'eau, sauf si on introduit un troisième type de molécules, amphiphile (=double-amour : une partie est hydrophile (car électriquement chargée), l'autre partie est hydrophobe ('lipophile') parce que non chargée). On en entend plutôt parler sous le nom d'émulsifiants ou de tensioactifs, par exemple.


Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Un piéton marche de nuit sur un trottoir, en ligne droite, à vitesse constante. La vitesse de l'ombre de sa tête sur l'asphalte diminue-t-elle, augmente-t-elle ou reste-t-elle constante lorsque le piéton s'approche du lampadaire responsable de cette ombre ?

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Topsy Turvy a écrit:Un piéton marche de nuit sur un trottoir, en ligne droite, à vitesse constante. La vitesse de l'ombre de sa tête sur l'asphalte diminue-t-elle, augmente-t-elle ou reste-t-elle constante lorsque le piéton s'approche du lampadaire responsable de cette ombre ?
Je suis incapable de faire une réponse théorique. Je suis tellement en morceaux que je ne sais plus faire un cosinus (ça serait la méthode élégante). Alors je vais essayer de prendre un exemple pour me représenter la chose. Mettons que le lampadaire soit à deux fois la hauteur de la tête, par rapport au trottoir. Au final, on a un triangle rectangle. Enfin deux, le premier a une base de la moitié du deuxième, et le même sommet. In fine, quelle que soit la distance du piéton au lampadaire, on a toujours la taille de l'ombre qui est le double de la distance au lampadaire. Si on dérive la distance pour avoir une vitesse, on garde ce facteur 2. or la vitesse est assumée constante. Donc la vitesse de l'ombre de la tête est constante aussi.
Truc rigolo, après réflexion, le coup des triangles marche même si on ne passe pas strictement sous la lumière. On aura des triangles différents, mais leur projection sur le plan vertical qui passe sous la lumière ne modifie pas les distances dans le sens de la marche.
Et ce qui est rigolo, c'est que pour ces deux cas, mon premier instinct a été de me dire "ça ralentit en approchant". Mais mon instinct m'a aussi dit qu'il fallait écrire pour être sur. J'ai écrit. J'ai alors compris.

RonaldMcDonald- Messages : 11679
Date d'inscription : 15/01/2019
Age : 48
Localisation : loin de chez moi, dans un petit coin de paradis
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Topsy Turvy a écrit:Un piéton marche de nuit sur un trottoir, en ligne droite, à vitesse constante. La vitesse de l'ombre de sa tête sur l'asphalte diminue-t-elle, augmente-t-elle ou reste-t-elle constante lorsque le piéton s'approche du lampadaire responsable de cette ombre ?
- Spoiler:
- Il a objectivement un OCD s'il se pose ce genre de question.

persntm 2- Messages : 633
Date d'inscription : 28/04/2023
Localisation : exerce ses doudounes d'homme
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
J'adore ton cheminement, RonaldMcDonald.
Je pense qu'on tend à se faire avoir (dans un sens ou dans l'autre, en pensant instinctivement à une accélération ou à une décélération) à cause de l'inégalité des vitesses de la tête et de son ombre.
Plus simplement (dans la mesure où c'est sauf erreur au programme des collèges), on est dans une situation d'homothétie.
Si le chapitre homothétie a sûrement été oublié, je pense que beaucoup de gens peuvent avoir un vague souvenir d'un "théorème de Thalès" (je mets des guillemets parce que l'expression ne désigne pas partout la même chose) :

Le rapport d'homothétie est ici égal au rapport entre la hauteur du lampadaire et la différence des hauteurs du lampadaire et du piéton. Par exemple un rapport de 2 si on a un piéton de 1,8 m et un lampadaire de 3,6 m. Dans la mesure où on considère une ombre au sol, le lampadaire est forcément plus grand que le piéton, le rapport d'homothétie est donc supérieur à 1. La vitesse de l'ombre de la tête sera donc un multiple fixe de la vitesse du piéton (3 fois plus rapide si piéton de 2 m et lampadaire de 3 m ; 1.5 fois plus rapide si piéton de 1 m et lampadaire de 3 m ;...).
On se représente peut-être mieux que la vitesse sera supérieure mais constante si on ne considère pas l'ombre projetée d'un piéton mais l'image projetée d'une diapositive. Si on fait pivoter un peu, à vitesse constante, le projecteur à diapo, l'image projetée subira un déplacement plus important que la diapo, mais également à vitesse constante (100 fois plus vite si l'écran de projection est à 10 m de la lampe alors que la diapo est à 10 cm de celle-ci). Il faut alors bien considérer une rotation avec la lampe comme point de pivot, ou un déplacement de la diapo et pas de la lampe. Et il ne s'agit que d'une approximation, la surface de projection ayant peu de chance d'être courbe, mais c'est pour illustrer par une situation différente mais comparable qu'on peut avoir une vitesse supérieure mais constante de ce qui est projeté (que ce soit une ombre ou une image).

Je pense qu'on tend à se faire avoir (dans un sens ou dans l'autre, en pensant instinctivement à une accélération ou à une décélération) à cause de l'inégalité des vitesses de la tête et de son ombre.
Plus simplement (dans la mesure où c'est sauf erreur au programme des collèges), on est dans une situation d'homothétie.
Si le chapitre homothétie a sûrement été oublié, je pense que beaucoup de gens peuvent avoir un vague souvenir d'un "théorème de Thalès" (je mets des guillemets parce que l'expression ne désigne pas partout la même chose) :

Le rapport d'homothétie est ici égal au rapport entre la hauteur du lampadaire et la différence des hauteurs du lampadaire et du piéton. Par exemple un rapport de 2 si on a un piéton de 1,8 m et un lampadaire de 3,6 m. Dans la mesure où on considère une ombre au sol, le lampadaire est forcément plus grand que le piéton, le rapport d'homothétie est donc supérieur à 1. La vitesse de l'ombre de la tête sera donc un multiple fixe de la vitesse du piéton (3 fois plus rapide si piéton de 2 m et lampadaire de 3 m ; 1.5 fois plus rapide si piéton de 1 m et lampadaire de 3 m ;...).
On se représente peut-être mieux que la vitesse sera supérieure mais constante si on ne considère pas l'ombre projetée d'un piéton mais l'image projetée d'une diapositive. Si on fait pivoter un peu, à vitesse constante, le projecteur à diapo, l'image projetée subira un déplacement plus important que la diapo, mais également à vitesse constante (100 fois plus vite si l'écran de projection est à 10 m de la lampe alors que la diapo est à 10 cm de celle-ci). Il faut alors bien considérer une rotation avec la lampe comme point de pivot, ou un déplacement de la diapo et pas de la lampe. Et il ne s'agit que d'une approximation, la surface de projection ayant peu de chance d'être courbe, mais c'est pour illustrer par une situation différente mais comparable qu'on peut avoir une vitesse supérieure mais constante de ce qui est projeté (que ce soit une ombre ou une image).

Dernière édition par Topsy Turvy le Sam 20 Mai 2023 - 9:05, édité 1 fois (Raison : oups, bug calcul rapport, sorry, vitesse d'autant plus petite que lampadaire relativement grand, of course)

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Dans Le Secret de la Licorne, Tintin, enfermé dans les caves du château de Moulinsart, tente de soulever une poutre pour l'utiliser comme bélier. Ne pouvant la soulever directement, il utilise une corde (faite de draps noués), enfilant celle-ci à travers un anneau dans le plafond, pour hisser la poutre. Est-ce que c'est crédible ?


Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Topsy Turvy a écrit:Dans Le Secret de la Licorne, Tintin, enfermé dans les caves du château de Moulinsart, tente de soulever une poutre pour l'utiliser comme bélier. Ne pouvant la soulever directement, il utilise une corde (faite de draps noués), enfilant celle-ci à travers un anneau dans le plafond, pour hisser la poutre. Est-ce que c'est crédible ?
- Spoiler:
- Ça va diviser par deux le poids, si je ne dis pas de bêtises, mais à mon idée il va suer des gouttes, voire se péter le dos.

persntm 2- Messages : 633
Date d'inscription : 28/04/2023
Localisation : exerce ses doudounes d'homme
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Une poulie ne fait que retransmettre la force. Si il attache la corde au milieu (ce qui semble cohérent avec l'objectif de faire un bélier), la force nécessaire sera la même que si il essaye de la mettre sur son épaule.
Mais ce n'est pas le seul élément à prendre en compte : il y a aussi la biomécanique. Via la poulie, il peut utiliser tous ses muscles, mais aussi tout le poids de son corps, alors qu'en haltérophile, il ne va utiliser que certains muscles, et le poids de son corps ne lui sera d'aucune utilité.
Dit autrement, si l'astuce de la poulie ne réduit pas la force nécessaire (enfin, il faut voir la configuration, mais le milieu dans les deux cas me semble raisonnable), elle augmente la force disponible.
Mais ce n'est pas le seul élément à prendre en compte : il y a aussi la biomécanique. Via la poulie, il peut utiliser tous ses muscles, mais aussi tout le poids de son corps, alors qu'en haltérophile, il ne va utiliser que certains muscles, et le poids de son corps ne lui sera d'aucune utilité.
Dit autrement, si l'astuce de la poulie ne réduit pas la force nécessaire (enfin, il faut voir la configuration, mais le milieu dans les deux cas me semble raisonnable), elle augmente la force disponible.

RonaldMcDonald- Messages : 11679
Date d'inscription : 15/01/2019
Age : 48
Localisation : loin de chez moi, dans un petit coin de paradis
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
En effet, il y a un risque de confondre poulie simple, qui ne fait que modifier la direction d'application d'une force, et palan, qui permet de réduire la force nécessaire. L'illustration qui suit me semble faciliter la compréhension, même si le format d'origine est un peu petit (et donc c'est flou) :
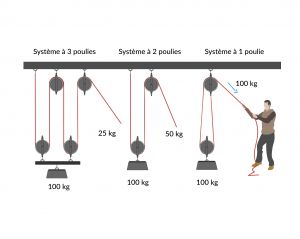
Les masses sont indiquées et non les forces, mais on peut arrondir à une force de 1000 N comme poids d'une masse de 100 kg (car g=~10).
Le cas du singe avec le miroir est aussi un cas où seule la direction est modifiée. On pourrait représenter ce qui se passe d'une autre manière, en considérant par exemple deux patineurs sur la glace, reliés par une corde. Si un seul des patineurs tire sur la corde, les patineurs se rapprochent, chacun avançant vers l'autre, à la même vitesse.
Hergé devait avoir des idées très très vagues au sujet des poulies, parce qu'il a même proposé d'abord une 'pseudo exploitation' carrément contreproductive :


La page qui propose cette image débunk aussi l'idée de la poulie :
https://tintinomania.com/tintin-poutre-licorne

Les masses sont indiquées et non les forces, mais on peut arrondir à une force de 1000 N comme poids d'une masse de 100 kg (car g=~10).
Le cas du singe avec le miroir est aussi un cas où seule la direction est modifiée. On pourrait représenter ce qui se passe d'une autre manière, en considérant par exemple deux patineurs sur la glace, reliés par une corde. Si un seul des patineurs tire sur la corde, les patineurs se rapprochent, chacun avançant vers l'autre, à la même vitesse.
Hergé devait avoir des idées très très vagues au sujet des poulies, parce qu'il a même proposé d'abord une 'pseudo exploitation' carrément contreproductive :

La page qui propose cette image débunk aussi l'idée de la poulie :
https://tintinomania.com/tintin-poutre-licorne

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Laurel et Hardy repeignent leur maison. Ils ont placé une échelle, appuyée, contre la façade.
a) Hardy commence à grimper. "Attention, lui dit Laurel, l'échelle est trop inclinée, elle va finir par glisser." "Idiot", répond Hardy, "si ça tient quand je suis sur le troisième échelon, ça tiendra aussi quand je serai sur le dernier échelon." A-t-il raison ?
b) Arrivé au milieu de l'échelle, Hardy prend peur et adhère au raisonnement de Laurel. Il redescend et dit à Laurel : "Puisque tu es si intelligent, monte toi-même. Comme tu es plus léger, tu as plus de chances d'atteindre le sommet sans que l'échelle ne glisse." A-t-il raison ?
[On supposera, pour simplifier, que seul le frottement avec le sol, et non avec le mur, assure la stabilité de l'échelle.]
Une autre question annexe concernant les bulles de savon, avant de proposer réponses du livre et d'ailleurs. Pourquoi est-ce qu'elles éclatent, parfois même avant de toucher le sol par exemple ?

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
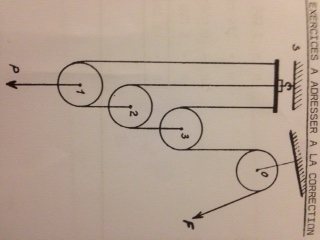
Au passage, pour vérifier si on a capté le principe des systèmes multi-poulies (palans) :
quelle est la fraction de la force P à exercer en F pour un maintien à l'équilibre ?
Retour à Lévy-Leblond. On va dire que Laurel et Hardy n'ont pas fait que de la peinture de bâtiment...
:max_bytes(150000):strip_icc()/HangingPicture5-58c1a1255f9b58af5cdf3de4.jpg)
quelle est la fraction de la force P à exercer en F pour un maintien à l'équilibre ?

Retour à Lévy-Leblond. On va dire que Laurel et Hardy n'ont pas fait que de la peinture de bâtiment...
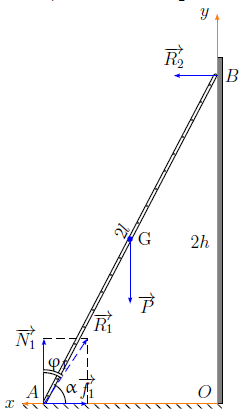
Un tableau est suspendu à un clou par une ficelle [dont les extrémités sont fixées de part et d’autres du tableau]. On néglige le frottement de la ficelle avec le clou et du tableau avec le mur.
a) L'équilibre peut-il exister dans d'autres positions que celle où le tableau est horizontal ?
b) L'équilibre est-il stable dans ladite position, horizontale, et dans les autres, s'il y en a ?
:max_bytes(150000):strip_icc()/HangingPicture5-58c1a1255f9b58af5cdf3de4.jpg)

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Topsy Turvy a écrit:Disons qu'au départ il y a un couple de vrai jumeaux, chacun agrippé à une extrémité d'une corde...
Euh, c'est pas que j'aie envie de pinailler à peine que je repasse par ici, hein, mais j'ai connu d'honnêtes vraies jumelles, tout ce qu'il y a de monozygotes. Eh bien, si l'une des deux était parfaitement svelte, sa frangine, en revanche, était très clairement obèse. (D'une obésité si morbide que je ne pense d'ailleurs pas qu'il aurait été judicieux de lui suggérer de se pendre à une corde...)
- Le singe monte-en-l'air, et Delphine et Marinette mangent des cochonneries.:
Dans le cadre de mon ancien boulot, j'ai beaucoup fait mumuse avec des poulies, des palans, et autres contre-poids.
La première réponse qui m'est venue a été : les 2 montent en même temps.
Et puis, j'ai réfléchi : que le singe grimpeur soit plus ou moins haut ou bas, on a toujours le même poids (ou masse ?) de part et d'autre (sauf si la corde est trèèèèèèèèès longue, et que le singe arrive à moins subir l'attraction terrestre ???). Ergo : il est donc logique que le miroir reste à la même hauteur.
Du coup, j'ai lu la réponse et les explications... et je ne comprends toujours pas. Dans l'exemple des patineurs, oui, s'ils pèsent le même poids (et mêmes résistances, tout ça), il me semble très logique qu'ils avancent en même temps.
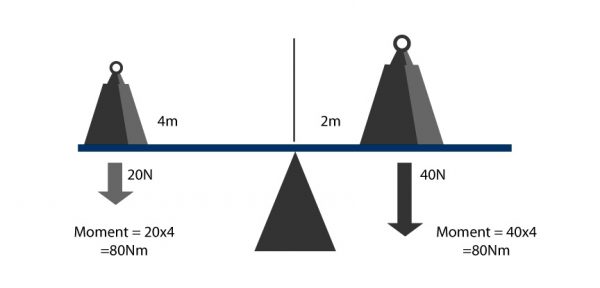
Edit : en fait, ayé, j'ai compris... grâce à l'illustration du "moment" (je ne connaissais pas ce terme) qui illustre les poids à l'équilibre selon leur éloignement par rapport au point d'équilibre.
N'empêche, ça me turlupine de trouver un résultat plus crétin en ayant réfléchi que je ne l'aurais fait en sortant la première ânerie qui me passe par la tête...
Pour le candy cane, je me suis fait avoir, en me disant que si c'était équilibré, alors le poids était forcément le même de chaque côté. J'explique mon erreur par la très faible attractivité que les sucreries exercent sur moi. J'aurais été beaucoup plus vigilant s'il avait fallu partager un bon vieux camembert, comme tout honnête énoncé d'un problème phsysico-mathématique est pourtant censé proposer, rognutudju.

Charv- Messages : 2388
Date d'inscription : 15/04/2018
Age : 47
Localisation : Lyon
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
- Accroche-toi au pinceau je retire l'échelle:
Allez, je tente :
A)Laurel a raison.
En effet, l'échelle est très inclinée. Ce qui fait que, sur la première marche, l'essentiel du poids repose sur les pieds de l'échelle.
Mais, plus Hardy monte, plus il s'éloigne également du pied sur le plan horizontal. Ce qui fait que davantage de poids s'exerce sur l'autre extrêmité de l'échelle, contre le mur, et de moins en moins sur le pied. Le pied subissant moins de poids/pression est d'autant plus susceptible de glisser d'une part, et d'autre part la pression qui s'exerce contre le mur tendra de plus en plus à repousser le pied sur un plan horizontal.
(Je ne sais pas si j'ai réussi à être clair ; disons que si on remplace l'échelle par un pont suspendu à l'horizontale, au fur et à mesure qu'on le traverse, on exerce moins de poids sur l'attache de départ, et de plus en plus sur l'attache d'arrivée.
Donc : plus l'échelle a de pied, plus elle est proche de l'horizontale, plus le poids se répartit sur chaque extrémité ; moins elle a de pied, plus elle est proche de la verticale, et plus le poids s'exerce surtout sur la base.)
B)Hardy a raison.
Pour les raisons que j'ai expliquées si dessus, Laurel (le maigre, donc) exercera moins de poids contre le mur quand il sera en haut, et aura donc moins tendance à repousser le pied sur le plan horizontal.
Le plus prudent est donc ou bien d'enlever du pied, ou que le plus maigre monte, et que le moins maigre lui "fasse le pied", comme on dit dans le jargon des grimpeurs à l'échelle.
Edit : si ces deux dégourdis avaient bossé dans mon équipe, je leur aurait dûment chauffé les oreilles en leur rappelant que, selon le droit du travail français-de-chez-nous, l'échelle est un moyen d'accès ET PAS UN POSTE DE TRAVAIL, ah mais !
Dernière édition par Charv le Dim 21 Mai 2023 - 20:31, édité 2 fois

Charv- Messages : 2388
Date d'inscription : 15/04/2018
Age : 47
Localisation : Lyon
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
- L'affaire du tableau:
D'expérience, pour avoir accroché un paquet de tableaux avec ce système, je confirme que l'équilibre peut exister dans d'autres positions qu'horizontale. J'aurais même tendance à dire qu'il existe SURTOUT dans d'autres positions qu'horizontale, ce système est super galère pour obtenir un tableau bien droit. Ta Marion Boddy-Evans, là, au lieu de se la jouer "chuis une artiste", elle pouvait pas aussi prendre un mètre et planter un python bien au centre, non ??? Faignasse !Topsy Turvy a écrit:
a) L'équilibre peut-il exister dans d'autres positions que celle où le tableau est horizontal ?
Euh, je suis pas sûr de comprendre. Si l'équilibre est atteint, c'est que c'est stable non ???Topsy Turvy a écrit:
b) L'équilibre est-il stable dans ladite position, horizontale, et dans les autres, s'il y en a ?
Si la question est : selon l'endroit ou l'équilibre est atteint, faut-il exercer plus ou moins de force pour le déséquilibrer, ou toujours la même ?
Alors ma réponse serait (à "l'instinct" !) : plus l'équilibre est proche du milieu du fil, plus grande sera la force nécessaire pour déséquilibrer le tableau. A l'inverse, plus l'équilibre est éloigné du milieu de fil, moins la force nécessaire pour déséquilibrer le tableau sera grande, je pense même qu'il pourrait "glisser tout seul" à partir d'un certain éloignement du centre.

Charv- Messages : 2388
Date d'inscription : 15/04/2018
Age : 47
Localisation : Lyon
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
- Viens pou-poulie, viens pou-poulie, vieeeeeeens.:
- Topsy Turvy a écrit:Au passage, pour vérifier si on a capté le principe des systèmes multi-poulies (palans) :
quelle est la fraction de la force P à exercer en F pour un maintien à l'équilibre ?
En théorie, F=P/4.
Mais, en pratique, avec le jeu des frottements, F devra être nettement plus important. D'ailleurs, selon la théorie, il suffirait de mettre 25 poulies pour n'avoir qu'à exercer une pichenette pour lever P. Or, même si P=0 ou presque, je souhaite bon courage à celui qui essaiera de lever P avec 25 poulies...
Tiens, d'ailleurs, au passage : saurait-on m'expliquer pourquoi, plus le diamètre de la poulie est grand, moins les forces de résistance s'exercent ??? Je soupçonne fort une histoire d'angle donné à la corde, mais j'avoue que, pour avoir vérifié le principe moulte fois, je ne l'ai jamais clairement expliqué...

Charv- Messages : 2388
Date d'inscription : 15/04/2018
Age : 47
Localisation : Lyon
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Charv


- Singerie :
- Bien essayé. Moralité, mieux vaut ne pas trop réfléchir.
En fait, il y a des forces qui tendent vers le bas et vers le haut et qui sont égales au départ (à l'équilibre), puisque les jumelles sont de même corpulence, sexy, en déshabillé du soir,... et retenues par une corde.
Donc, au départ, les forces sont à l'équilibre, avec la tension de la corde égalisant le poids de chacune des beautés, par exemple environ 600 N pour 60 kg. On dessinerait quatre forces représentant chacune 600 N, deux forces dirigées vers le bas (le poids de chacune) et deux forces dirigées vers le haut (la tension de la corde qui retient les soeurs). Si les forces vers le haut et vers le bas ne s'égalisaient pas, on aurait un mouvement.
L'illustration n'est pas parfaite, mais ça aide peut-être à se représenter les forces au départ :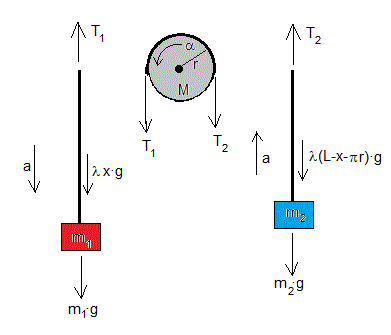
Quand l'une d'elle (mais je ne vais pas dire laquelle, pour qu'on ne m'accuse pas de favoritisme ni de harcèlement ni rien) tire sur la corde, elle augmente la force vers le haut qui part de son centre de gravité (oui, là, au niveau du joli ventre dénudé), mais aussi à partir du centre de gravité de sa soeur, la corde transmettant la force appliquée, la tension de la corde. Les forces vers le haut dépassent alors les forces vers le bas et elles s'élèvent toutes les deux.
- Laure elle est hardie :
- Joli raisonnement, conclusion correcte mais la situation évolue d'une autre manière. Cette fois-ci on est dans une situation où il faut tenir compte du moment de force. Plus Hardy monte haut sur l’échelle, plus la réaction horizontale due au frottement au sol doit être importante, le moment de la force P augmentant avec la distance au sol. La réaction verticale N (au pied de l’échelle) est toujours égale à P. Si Hardy est trop haut, il se peut que le coefficient de frottement soit trop faible pour assurer une force de frottement suffisante.
Le truc vraiment rigolo, c'est que les forces considérées sont proportionnelles au poids, Laurel tombera donc avec l'échelle à la même hauteur que Hardy.
J'ajoute qu'on peut tester en appuyant des trucs (cartons,...) comme une échelle. Plus c'est incliné, plus le truc risque de glisser, sous l'effet de son propre poids. Si la force de frottement est comparable et les dimensions aussi, on doit alors observer que les trucs se cassent la gueule à la même inclinaison, quels que soient les poids. Oui, pas besoin de monter dessus, il suffit de considérer le poids de l'objet incliné. On n'a pas la preuve du niveau intermédiaire avant bascule, mais ça c'est facile à se représenter. Si le truc est vertical, il ne glissera pas. S'il est très incliné, il ne tiendra pas. L'entre-deux est assez logique, même si pas forcément intuitif.
- Laurie Zontale:
- il existe SURTOUT dans d'autres positions qu'horizontale
On est d'accord.
a) Pour qu'il y ait équilibre, il faut que le moment de tension de la corde par rapport à G soit le même en A et en B, c'est-à-dire que soit vérifié
sin α = sin ß
Ainsi, en plus de la position d'équilibre horizontale (α = ß), il existe deux autres positions d'équilibre, symétriques par rapport à la verticale, obliques, telles que α + ß = π (180°).
plus l'équilibre est proche du milieu du fil, plus grande sera la force nécessaire pour déséquilibrer
En fait, non. Et ça explique un peu pourquoi c'est l'horreur d'arriver à l'horizontale et de la maintenir avec ce système.
b) La position d'équilibre horizontale est instable : un léger déplacement augmente le moment total dans la direction du déplacement (ß > α par exemple). Les deux positions obliques correspondent à un équilibre stable pour les raisons opposées.
Je repasse demain pour préciser et illustrer.
- Reviens Pauline :
- F=P/4
Try again. C'est un système typique d'exercice théorique, ce serait trop débile en vrai.
pourquoi, plus le diamètre de la poulie est grand, moins les forces de résistance s'exercent
Plus tu augmentes la surface de contact entre la poulie et la corde, plus tu obtiens d'adhérence entre elles, à savoir le bon frottement, celui que tu veux, parce qu'il entraîne la rotation de la poulie plutôt que le glissement de la corde sur la poulie.

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Le "système de poulies" en image un peu plus haut répartit la force sur deux brins à chacune des trois premières "poulies". Une force initiale P de 800 N serait retenue pour 400 N par la "poulie" 2, puis 200 N par la "poulie" 3 et enfin seulement 100 N par la force F. Ce "montage" est typiquement un exercice de raisonnement pur et pas un cas pratique de la vraie vie. Il réduit (en théorie, en effet, mieux vaut le préciser) la force à exercer par 2∙2∙2 = 2^3 = 8. Mais juste pour que le montage ne se pète pas la gueule. On n'est même pas dans une situation de palan (système avec poulies fixe(s) et mobile(s). C'est juste une suspension avec répartition de force, basta. Sorry pour l'exercice bidon. La prochaine fois je regarderais à deux fois avant de balancer le premier truc marrant parce qu'inhabituel.
Le tableau, dans l'idéal, ce serait un peu comme ça :
https://www.ilephysique.net/img/forum_img/0252/forum_252825_1.gif
En vrai, c'est rarement aussi idyllique...
Le tableau, dans l'idéal, ce serait un peu comme ça :
https://www.ilephysique.net/img/forum_img/0252/forum_252825_1.gif
En vrai, c'est rarement aussi idyllique...
- Tableau de travers :
- Voilà, j'ai beaucoup hésité à comment formuler, mais je crois que je tiens un truc, pour le tableau.
L'illustration de Lévy-Leblond est la suivante :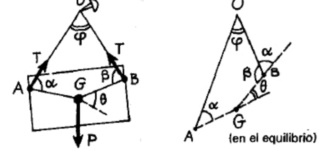
On va considérer les forces partant de A et de B, qui voudraient entraîner une rotation du système dans un sens et dans l'autre. Si on a un monstre bol, on arrive à mettre le tableau à l'horizontal, en équilibre, mais équilibre précaire. Dès que le truc commence à basculer, les forces le long du fil ne peuvent plus se compenser l'une l'autre, parce que leur direction change. L'une voit sa direction tourner en direction du centre de gravité (force en A sur le schéma) tandis que l'autre voit sa direction s'en éloigner (force en B sur le schéma). C'est la composante tangentielle qui nous intéresse. Donc pas celle qui est orientée selon l'axe "extrémité de ficelle - centre de gravité", mais celle qui est orientée perpendiculairement à cet axe. C'est la raison pour laquelle on s'intéresse au sinus de l'angle formé à chaque point de fixation (ci-dessous, O serait le centre de gravité du tableau, P le point B, la flèche bleue serait le long du fil, oui, ça ne correspond pas exactement, mais c'est l'idée) :
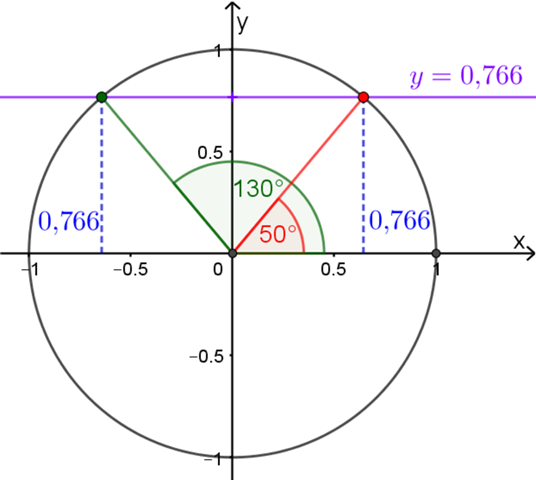
Le truc rigolo, c'est qu'on a plusieurs angles qui ont le même sinus (une infinité en fait, mais deux qui nous intéressent ici). Le cercle trigonométrique ci-dessous aide à visualiser le sinus d'un angle (segment rouge à gauche ; valeur 0,766 à droite) :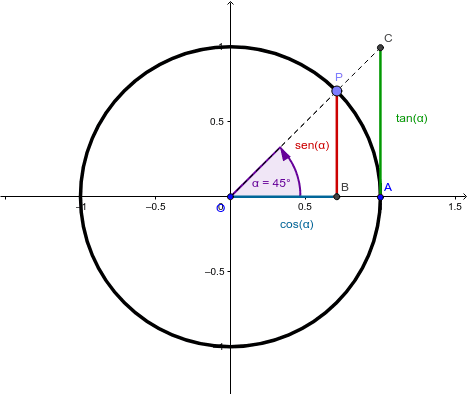
Parenthèse inutile ici mais j'en profite : si on fait tourner, on retombe périodiquement sur les mêmes valeurs, la courbe de la fonction sinus est dite sinusoïdale :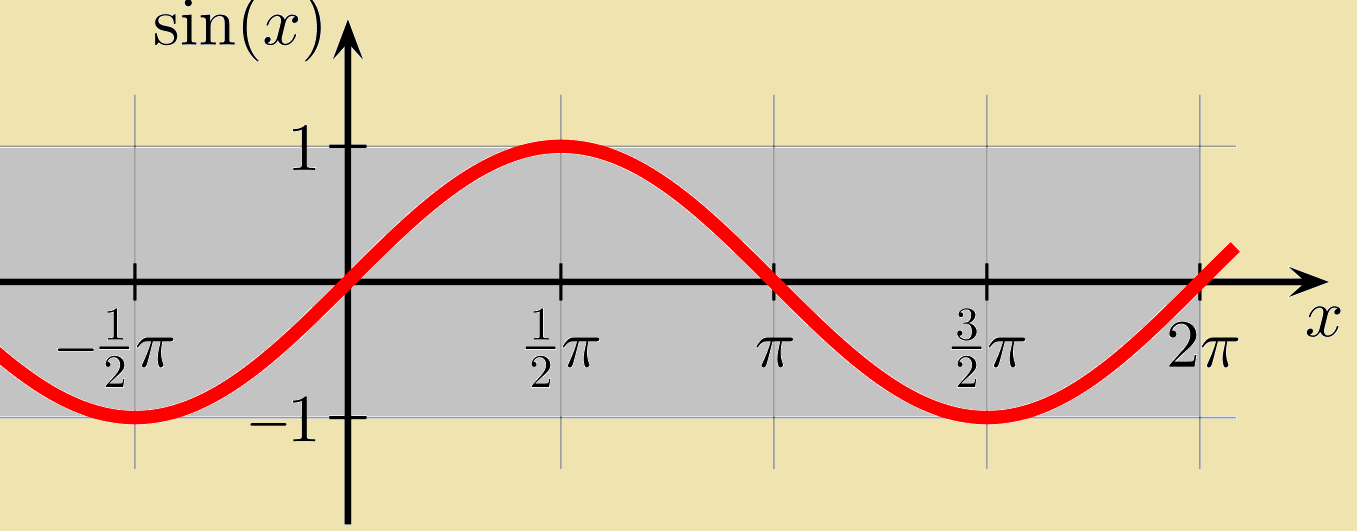
Retour au tableau. Le bordel avec les forces et moments de forces explique pourquoi on rame à placer et maintenir un tableau à l'horizontale avec ce système. Le moindre déséquilibre fait basculer vers un équilibre plus stable, tableau de travers, dans un sens ou dans l'autre. Si on essaie de remettre le machin droit, on doit le mettre parfaitement droit, sinon il bascule à nouveau direct vers un équilibre de travers, en penchant d'un côté ou de l'autre. S'il ne bascule pas direct, il basculera à la première pichenette. Seules les forces de frottement limitent l'étendue du désastre.

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Comment peut-on, dans certains cas, survivre à un coup de foudre ?
La bulle de savon électrisée voit son volume augmenter, par l'effet répulsif des charges de même nature, mais très légèrement. Elle s'allonge dans le sens d'un champ électrique uniforme.
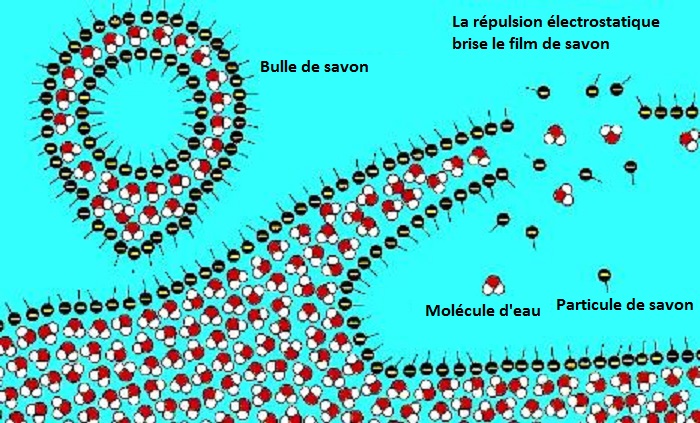
La bulle de savon éclate quand ses couches externe et interne entrent en contact. Elle est en effet constituée de trois couches : une couche de molécules d'eau prise en sandwich entre deux couches de molécules amphiphiles. Si on perce la bulle, ou si l'eau a le temps de s'écouler vers le bas, les parties chargées des molécules amphiphiles se repoussent mutuellement.
L'illustration ci-dessous n'est pas parfaite, mais ça donne l'idée :
Pas Lévy-Leblond non plus, une question de comparaison :
Avec la même quantité d'énergie que celle requise pour élever de 1 °C la température de 30 ml d'eau liquide (par exemple pour que la température de l'eau passe de 20°C à 21°C), quelle serait la masse d'un objet soulevé de 1 m (en partant du sol). Sans considérer de déperdition énergétique, ni de résistance de l'air, ni de considérations existentielles du genre 'le sens de la vie' ni rien. On peut arrondir les valeurs, par exemple en considérant g=10m/s^2)


Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
On sait que la charge électrique est quantifiée. Les énoncés suivants de ce fait sont-ils équivalents ?
a) il existe une charge électrique minimale non nulle (plus petite unité de charge) ;
b) toute charge électrique est multiple entier (positif ou négatif) d'une charge électrique élémentaire ;
c) la charge électrique n'est pas une grandeur continue (prenant toutes les valeurs réelles).
- Pour survivre foudroyé par l'orage :
- Il suffit que le courant soit évacué sans traverser les organes internes vitaux, en empruntant la surface du corps si elle est particulièrement conductrice (humide de transpiration — ou de peur ?), ou mieux encore les vêtements (mouillés par la pluie).
- Avec autant d'énergie que pour élever de 1°C la température de 30ml d'eau, on élève de 1 mètre... :
Environ 800 grammes de plus que ça :
Calculs :
La capacité thermique massique de l'eau est de ~4,186[ J] par [g] par [°C].
30 ml d'eau pèse ~30 [g] (plus précisément, 1 [l] d'eau pèse 1 [kg] à 4 [°C]).
Pour 30 [g] et 1 [°C], l'énergie est de ~4,186 fois 30 = ~125,58 [J].
L'énergie peut être exprimée en [J], mais aussi en [N∙m], entre autres.
L'accélération de pesanteur (g = ~9,81) est en [m]/[s^2], mais aussi [N]/[kg].
On détermine la masse déplacée sur 1 [m] en divisant l'énergie par g.
~125,58 [N∙m] divisé par ~9,81 [N]/[kg]donne donc ~12,8 [kg] par [m].
La capacité thermique massique de l'eau est vraiment élevée, relativement.
J'ai précisé dans la donnée de considérer de l'eau à l'état liquide.
La glace a une capacité thermique massique de 2,06 [J] par [g] par [°C]
(ce qui est donc environ moitié moins pour pour l'eau liquide).

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
pour les trois phrases électriques : si je lis bien (mais j'ai du mal), l'énoncé (b) stipule qu'on est dans le monde des entiers stricts (avec juste un multiplicateur, commun à toutes les charges). (a) et (c) me paraissent à peu près équivalents, mais ils permettent plus de liberté - par exemple 1,5 si la charge minimale est 1. (c) est moins contraignant que (a), puisqu'il ne précise pas où se situe la zone ou les charges possibles sont non continues, alors que (a) oblige a ce que la zone entre 0 et le minimum soit impossible..

RonaldMcDonald- Messages : 11679
Date d'inscription : 15/01/2019
Age : 48
Localisation : loin de chez moi, dans un petit coin de paradis
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Avant de balancer la réponse de Lévy-Leblond, je précise qu'il y a une différence subtile entre la considération d'un mathématicien et celle d'un physicien, en particulier pour l'assertion (c).
plus de liberté - par exemple 1,5 si la charge minimale est 1
Il y aurait contradiction. L'unité (1 dans l'hypothèse ci-dessus) doit être plus petite ou égale à l'ajout (0,5 dans l'hypothèse ci-dessus). L'ajout doit donc être un nombre entier (ou nul) de multiple de 1 (si la charge minimale est 1). Ceci parce qu'on ne parle pas tant d'une valeur minimale (de départ) que d'un palier minimal (à partir de rien, mais aussi entre les valeurs suivantes). Ou, plus exactement, la valeur minimale implique des sauts multiples de cette valeur minimale.
plus de liberté - par exemple 1,5 si la charge minimale est 1
Il y aurait contradiction. L'unité (1 dans l'hypothèse ci-dessus) doit être plus petite ou égale à l'ajout (0,5 dans l'hypothèse ci-dessus). L'ajout doit donc être un nombre entier (ou nul) de multiple de 1 (si la charge minimale est 1). Ceci parce qu'on ne parle pas tant d'une valeur minimale (de départ) que d'un palier minimal (à partir de rien, mais aussi entre les valeurs suivantes). Ou, plus exactement, la valeur minimale implique des sauts multiples de cette valeur minimale.

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
C'est non précisé dans l'énoncé. Si c'est sous-tendu, effectivement, on se retrouve à dire trois fois la même chose. Je suis parti de l'énoncé, pas d'hypothèses supplémentaires que j'aurais été sensé connaitre.
Ou alors un joue sur les différents sens que "quantifié" peut signifier. Auquel cas la question est mal posée, puisqu'une information cruciale est passée via un vocable à double sens.
Ou alors un joue sur les différents sens que "quantifié" peut signifier. Auquel cas la question est mal posée, puisqu'une information cruciale est passée via un vocable à double sens.

RonaldMcDonald- Messages : 11679
Date d'inscription : 15/01/2019
Age : 48
Localisation : loin de chez moi, dans un petit coin de paradis
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Peut-être, mais je n'arrive pas à voir quel sens de quantifier poserait problème.
Par contre, la réponse formulée se détache selon moi du sens de 'équivalent'.
https://www.cnrtl.fr/definition/équivalent
Il y a une question 'supplémentaire' proposée, je la dépose au passage :
Que se passerait-il s'il existait des charges élémentaires de rapport irrationnel, par exemple q et q' avec q' égale racine carrée de 2 fois q ?
Sorry pour l'absence de mise en forme, flemme de me prendre la tête avec.]
[Ci-dessous, je laisse les indices 1 et 2 à taille normale]
La réponse de Lévy-Leblond :
Oui, les trois énoncés sont équivalents, au moins du point de vue du physicien, sinon du mathématicien. On a les implications logiques évidentes b) => a) => c). Par ailleurs, si a) est vraie, soit q1 la charge minimale et q2 une autre charge ; alors, si q2 n'est pas un multiple entier de q1, on pourrait, par combinaison linéaire à coefficients entiers relatifs de q1 et q2, former une charge plus petite que q1 (par exemple, si q2 = [racine carrée de 2 fois q] alors q2 - q1 < q1), contrairement à l'hypothèse. Donc a) => b). Enfin pour que c) soit vraie et a) et b) fausses, il faudrait par exemple que les charges puissent prendre, par rapport à une certaine charge fondamentale, toutes les valeurs rationnelles (ou algébriques) et celles-là seulement. Mais ces ensembles de nombres étant denses dans celui des réels, le physicien ne pourrait distinguer cette situation du cas où les charges prennent toutes les valeurs réelles.
Je pense qu'on est d'accord qu'il y a un souci dans la réponse formulée dans le livre, par le changement de logique, qui mélange d'abord allègrement équivalence et implication logique pour virer à véracité si blabla non vrais. La dernière phrase m'échappe, même en me référant à mon ami wiki : https://fr.wikipedia.org/wiki/Partie_dense
A. − Attribuer une quantité, une valeur quantitative à (une chose concrète ou abstraite); évaluer et exprimer en chiffres. Synon. chiffrer, mesurer, nombre. ...
B. − Spécialement
1. LOG. Attribuer une quantité à (un terme); opérer une quantification. ...
2. SC., PHYS. Déterminer la quantité de, mesurer quelque chose; opérer une quantification, appliquer une loi de quantification à (une grandeur physique). ...
https://www.cnrtl.fr/definition/quantifier
Par contre, la réponse formulée se détache selon moi du sens de 'équivalent'.
https://www.cnrtl.fr/definition/équivalent
Il y a une question 'supplémentaire' proposée, je la dépose au passage :
Que se passerait-il s'il existait des charges élémentaires de rapport irrationnel, par exemple q et q' avec q' égale racine carrée de 2 fois q ?
Sorry pour l'absence de mise en forme, flemme de me prendre la tête avec.]
[Ci-dessous, je laisse les indices 1 et 2 à taille normale]
La réponse de Lévy-Leblond :
Oui, les trois énoncés sont équivalents, au moins du point de vue du physicien, sinon du mathématicien. On a les implications logiques évidentes b) => a) => c). Par ailleurs, si a) est vraie, soit q1 la charge minimale et q2 une autre charge ; alors, si q2 n'est pas un multiple entier de q1, on pourrait, par combinaison linéaire à coefficients entiers relatifs de q1 et q2, former une charge plus petite que q1 (par exemple, si q2 = [racine carrée de 2 fois q] alors q2 - q1 < q1), contrairement à l'hypothèse. Donc a) => b). Enfin pour que c) soit vraie et a) et b) fausses, il faudrait par exemple que les charges puissent prendre, par rapport à une certaine charge fondamentale, toutes les valeurs rationnelles (ou algébriques) et celles-là seulement. Mais ces ensembles de nombres étant denses dans celui des réels, le physicien ne pourrait distinguer cette situation du cas où les charges prennent toutes les valeurs réelles.
Je pense qu'on est d'accord qu'il y a un souci dans la réponse formulée dans le livre, par le changement de logique, qui mélange d'abord allègrement équivalence et implication logique pour virer à véracité si blabla non vrais. La dernière phrase m'échappe, même en me référant à mon ami wiki : https://fr.wikipedia.org/wiki/Partie_dense
Dernière édition par Topsy Turvy le Jeu 25 Mai 2023 - 19:38, édité 1 fois (Raison : indice 2 partout, c'était un bug dû à la copie du pdf)

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
En fait, tu viens de résumer (mieux que je n'aurais su le faire) mon problème avec tous les tests de logique et autres tests psychotechniques. Il y a toujours un moment ou, à force d'augmenter la difficulté, la question n'est plus de trouver la réponse, mais de deviner comment a pensé la personne qui a conçu les questions.

RonaldMcDonald- Messages : 11679
Date d'inscription : 15/01/2019
Age : 48
Localisation : loin de chez moi, dans un petit coin de paradis
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
la question n'est plus de trouver la réponse, mais de deviner comment a pensé la personne qui a conçu les questions
Tu ne t'en es peut-être pas rendu compte en grandissant, mais c'est le cas dès l'école élémentaire. Les enfants d'enseignant se distinguent, mais pas tant parce que leurs parents les feraient étudier plus. Les gosses d'enseignants savent en général comment fonctionne un enseignant typique, parce qu'ils vivent avec un enseignant. Ça peut être particulièrement criant au primaire, mais encore au collège et au lycée.
Tu ne t'en es peut-être pas rendu compte en grandissant, mais c'est le cas dès l'école élémentaire. Les enfants d'enseignant se distinguent, mais pas tant parce que leurs parents les feraient étudier plus. Les gosses d'enseignants savent en général comment fonctionne un enseignant typique, parce qu'ils vivent avec un enseignant. Ça peut être particulièrement criant au primaire, mais encore au collège et au lycée.

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Tiens, je n'avais jamais pensé à ça. Sans doute parce que moi, je leur mettais la misère, aux enfants d'enseignants. Mon père avait fait Centrale Paris, et j'ai grandi au milieu de problèmes de maths/probas que je m'entrainais à faire de tête. En comparaison, un fils de prof n'avait aucune chance.
Mais non, la maison n'était pas pleine de tests psychotechniques. Ce qui explique que plus tard, j'ai pu avoir des surprises.
Pour cette histoire de quantification, ça peut vouloir dire "qui a une quantité", donc continue, ou "qui a des quantas", donc discrète.
Mais non, la maison n'était pas pleine de tests psychotechniques. Ce qui explique que plus tard, j'ai pu avoir des surprises.
Pour cette histoire de quantification, ça peut vouloir dire "qui a une quantité", donc continue, ou "qui a des quantas", donc discrète.

RonaldMcDonald- Messages : 11679
Date d'inscription : 15/01/2019
Age : 48
Localisation : loin de chez moi, dans un petit coin de paradis
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
"qui a une quantité"
oui, c'est mon interprétation, la première définition du CNRTL :
Attribuer une quantité, une valeur quantitative à (une chose concrète ou abstraite); évaluer et exprimer en chiffres. Synon. chiffrer, mesurer, nombre. ...
donc continue
J'ai l'impression que tu impliques "dans ℝ". Mais je peux quantifier des trucs dans ℕ (des gens par exemple, que je compte par unité entière).
oui, c'est mon interprétation, la première définition du CNRTL :
Attribuer une quantité, une valeur quantitative à (une chose concrète ou abstraite); évaluer et exprimer en chiffres. Synon. chiffrer, mesurer, nombre. ...
donc continue
J'ai l'impression que tu impliques "dans ℝ". Mais je peux quantifier des trucs dans ℕ (des gens par exemple, que je compte par unité entière).

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Du haut d'une colline, vous observez un nuage isolé qui se déplace dans le ciel. Vous observez également son ombre sur la plaine et vous pouvez estimer la taille de cette ombre et sa vitesse. De vos observations faites uniquement du point où vous vous trouvez, pouvez-vous déduire :
a) la taille du nuage ?
b) sa vitesse ?
c) son altitude ?

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Furet et polystyrène...

Oui partout pour le nuage. Les rayons du soleil nous arrivant parallèles entre eux, l'ombre aura les dimensions et la vitesse du nuage. Connaissant ainsi les dimensions du nuage, on peut estimer son altitude, par une estimation de sa taille apparente. On peut se représenter comment en reprenant l'illustration de l'homothétie. Si on tend le bras pour chercher à couvrir le nuage de la main, ou l'encadrer entre deux doigts écartés, l'estimation de cette petite mesure (main) et cette petite distance (oeil-main) permet d'obtenir l'altitude du nuage dont on connaît les dimensions (égales à celles de son ombre).


Oui partout pour le nuage. Les rayons du soleil nous arrivant parallèles entre eux, l'ombre aura les dimensions et la vitesse du nuage. Connaissant ainsi les dimensions du nuage, on peut estimer son altitude, par une estimation de sa taille apparente. On peut se représenter comment en reprenant l'illustration de l'homothétie. Si on tend le bras pour chercher à couvrir le nuage de la main, ou l'encadrer entre deux doigts écartés, l'estimation de cette petite mesure (main) et cette petite distance (oeil-main) permet d'obtenir l'altitude du nuage dont on connaît les dimensions (égales à celles de son ombre).

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Topsy Turvy a écrit:Du haut d'une colline, vous observez un nuage isolé qui se déplace dans le ciel. Vous observez également son ombre sur la plaine et vous pouvez estimer la taille de cette ombre et sa vitesse. De vos observations faites uniquement du point où vous vous trouvez, pouvez-vous déduire :
a) la taille du nuage ?
b) sa vitesse ?
c) son altitude ?
- Spoiler:
Oui aux trois.
Déjà si on connaît la taille du Soleil, la distance Terre-Soleil, on peut mesurer en posant ses doigts entre son œil et le nuage combien de Soleil le nuage prend de place dans le ciel, on a l'angle qu'il occupe par rapport à nous. On peut imaginer le cône qui part de nous et qui englobe le nuage.
Si on mesure la taille de l'ombre du nuage, ça nous donne une info sur l'angle qu'occupe le nuage par rapport au Soleil, si on imagine le dessin on imagine un cône avec comme base l'ombre et comme pointe le Soleil.
Il y a deux cônes, il n' y a qu'un seul endroit où les faisceaux se croisent. On connaît la distance. C'est gagné.
Pour connaître l'altitude faut mesurer l'angle entre l'horizon et le nuage et prendre la distance fois le sinus de l'angle.
Avec l'angle du cône et la distance au nuage on a directement la taille du nuage.
Et pour la vitesse c'est comme tout à l'heure avec le lampadaire, c'est le théorème de Thales, ça doit être un truc du genre v = v_ombre * (distance Terre Soleil - altitude) / distance Terre-Soleil.
câlin- Messages : 807
Date d'inscription : 13/09/2022
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Oui aux trois.
En effet, mais les raisonnements ne tiennent pas, il faut y apporter quelques corrections.
on imagine un cône avec comme base l'ombre et comme pointe le Soleil
Non, cette représentation considère le Soleil comme un point, ce qu'on ne peut pas faire. Les dimensions du Soleil sont en fait GIGANTESQUES et il nous paraît 'petit' parce qu'il est HYPER LOIN. Le diamètre du soleil est d'environ 110 fois celui de la Terre et on fait tenir environ 110 fois le Soleil entre lui et la Terre. Toute représentation visuelle statique où on aurait l'impression de voir en même temps le Soleil et la Terre est fausse, les proportions ne peuvent pas être respectées.
l'angle qu'occupe le nuage par rapport au Soleil
Il n'y a en fait pas de tel angle, le Soleil n'étant pas considérable comme un point. On considère ici les rayons du Soleil comme parallèles, les dimensions de l'ombre projetée du nuage correspondant donc aux dimensions du nuage.
mesurer l'angle entre l'horizon et le nuage et prendre la distance fois le sinus de l'angle

En admettant qu'on connaisse l'hypothèse du triangle rectangle considéré, donc la distance entre le point de mesure de l'angle et le nuage. Ce qu'on n'a pas. Par ailleurs, si on est sur une colline, le triangle ne serait pas un triangle rectangle.
pour la vitesse c'est comme tout à l'heure avec le lampadaire
Même souci et même rectification et simplification qu'en début de ce message. On considère les rayons de soleil comme parallèles, la vitesse de l'ombre est identique à la vitesse du nuage, de même que les dimensions de ces objets sont les mêmes.
si on connaît la taille du Soleil, la distance Terre-Soleil, on peut mesurer en posant ses doigts entre son œil et le nuage combien de Soleil le nuage prend de place dans le ciel, on a l'angle qu'il occupe par rapport à nous. On peut imaginer le cône qui part de nous et qui englobe le nuage.
Cette logique tient, en effet, mais pour obtenir dès cette étape l'altitude du nuage (connaissant déjà ses dimensions). J'ai une préférence pour utiliser le principe avec la main tendue pour faire tenir le nuage entre l'écartement des doigts, les valeurs estimées ne reposant pas sur la mémorisation de valeurs numériques liées aux objets célestes.
En fait, j'avais proposé une réponse qui colle au livre en fin de mon message précédent, sous les images d'électrostatique, avec une précision de méthode d'estimation de l'altitude basée sur l'image de l'homothétie. Comme ce n'était pas en spoiler, la réponse s'est retrouvée dissimulée en clair, manifestement. My bad.
Merci pour la participation !

Si j'ai mal compris des morceaux de réponse, il ne faut pas hésiter à me pointer où il y aurait incompréhension mutuelle.
En effet, mais les raisonnements ne tiennent pas, il faut y apporter quelques corrections.
on imagine un cône avec comme base l'ombre et comme pointe le Soleil
Non, cette représentation considère le Soleil comme un point, ce qu'on ne peut pas faire. Les dimensions du Soleil sont en fait GIGANTESQUES et il nous paraît 'petit' parce qu'il est HYPER LOIN. Le diamètre du soleil est d'environ 110 fois celui de la Terre et on fait tenir environ 110 fois le Soleil entre lui et la Terre. Toute représentation visuelle statique où on aurait l'impression de voir en même temps le Soleil et la Terre est fausse, les proportions ne peuvent pas être respectées.
l'angle qu'occupe le nuage par rapport au Soleil
Il n'y a en fait pas de tel angle, le Soleil n'étant pas considérable comme un point. On considère ici les rayons du Soleil comme parallèles, les dimensions de l'ombre projetée du nuage correspondant donc aux dimensions du nuage.
mesurer l'angle entre l'horizon et le nuage et prendre la distance fois le sinus de l'angle
En admettant qu'on connaisse l'hypothèse du triangle rectangle considéré, donc la distance entre le point de mesure de l'angle et le nuage. Ce qu'on n'a pas. Par ailleurs, si on est sur une colline, le triangle ne serait pas un triangle rectangle.
pour la vitesse c'est comme tout à l'heure avec le lampadaire
Même souci et même rectification et simplification qu'en début de ce message. On considère les rayons de soleil comme parallèles, la vitesse de l'ombre est identique à la vitesse du nuage, de même que les dimensions de ces objets sont les mêmes.
si on connaît la taille du Soleil, la distance Terre-Soleil, on peut mesurer en posant ses doigts entre son œil et le nuage combien de Soleil le nuage prend de place dans le ciel, on a l'angle qu'il occupe par rapport à nous. On peut imaginer le cône qui part de nous et qui englobe le nuage.
Cette logique tient, en effet, mais pour obtenir dès cette étape l'altitude du nuage (connaissant déjà ses dimensions). J'ai une préférence pour utiliser le principe avec la main tendue pour faire tenir le nuage entre l'écartement des doigts, les valeurs estimées ne reposant pas sur la mémorisation de valeurs numériques liées aux objets célestes.
En fait, j'avais proposé une réponse qui colle au livre en fin de mon message précédent, sous les images d'électrostatique, avec une précision de méthode d'estimation de l'altitude basée sur l'image de l'homothétie. Comme ce n'était pas en spoiler, la réponse s'est retrouvée dissimulée en clair, manifestement. My bad.
Merci pour la participation !
Si j'ai mal compris des morceaux de réponse, il ne faut pas hésiter à me pointer où il y aurait incompréhension mutuelle.

Topsy Turvy- Messages : 8367
Date d'inscription : 10/01/2020
 Re: La physique en questions (de Jean-Marc Lévy-Leblond)
Re: La physique en questions (de Jean-Marc Lévy-Leblond)
En effet il y avait la réponse au-dessus mais le furet polystyréné avait capté toute mon attention.
J'y avais jamais pensé mais en fait la raison pour laquelle on voit nette l'ombre d'un nuage est qu'il est hyper proche de nous en comparaison du Soleil. J'imagine que l'ombre de Vénus doit être beaucoup plus floue à cause de son éloignement.
Avec ton raisonnement ce qu'on obtient est la distance entre nous et le nuage, ça donne l'altitude si le nuage est juste au-dessus à la verticale, mais s'il est proche de l'horizon, il faudrait utiliser un niveau à bulle, et connaître l'altitude de notre position pour en déduire l'altitude du nuage.
Et pour l'échelle j'ai une question. Tu dis que la stabilité de l'échelle ne dépend pas du poids appliqué dessus. Ça veut dire que si une poussière se dépose dessus, un éléphant qui se pose au même endroit a la même stabilité. Donc ça veut dire que si une échelle est stable posée sans rien, son propre poids ne la déstabilise pas, alors n'importe qui peut monter dessus et elle sera toujours stable ? Ça me paraît contre-intuitif.
À mon tour maintenant de poser une question. Laurel et Hardy sont en été et viennent de finir le dernier pot de glace à la vanille. Il fait trop chaud. Hardy a alors une idée de génie : pourquoi ne pas ouvrir la porte du congélateur, pour refroidir la pièce ? Cela va-t-il fonctionner ?
J'y avais jamais pensé mais en fait la raison pour laquelle on voit nette l'ombre d'un nuage est qu'il est hyper proche de nous en comparaison du Soleil. J'imagine que l'ombre de Vénus doit être beaucoup plus floue à cause de son éloignement.
Avec ton raisonnement ce qu'on obtient est la distance entre nous et le nuage, ça donne l'altitude si le nuage est juste au-dessus à la verticale, mais s'il est proche de l'horizon, il faudrait utiliser un niveau à bulle, et connaître l'altitude de notre position pour en déduire l'altitude du nuage.
Et pour l'échelle j'ai une question. Tu dis que la stabilité de l'échelle ne dépend pas du poids appliqué dessus. Ça veut dire que si une poussière se dépose dessus, un éléphant qui se pose au même endroit a la même stabilité. Donc ça veut dire que si une échelle est stable posée sans rien, son propre poids ne la déstabilise pas, alors n'importe qui peut monter dessus et elle sera toujours stable ? Ça me paraît contre-intuitif.
À mon tour maintenant de poser une question. Laurel et Hardy sont en été et viennent de finir le dernier pot de glace à la vanille. Il fait trop chaud. Hardy a alors une idée de génie : pourquoi ne pas ouvrir la porte du congélateur, pour refroidir la pièce ? Cela va-t-il fonctionner ?
câlin- Messages : 807
Date d'inscription : 13/09/2022
Page 1 sur 4 • 1, 2, 3, 4 
 Sujets similaires
Sujets similaires» Rencontre à la cité fertile 25,26,27 juin (Etienne Klein et Jean-Marc Jancovici)
» Rencontre à la cité fertile 25,26,27 juin (Etienne Klein et Jean-Marc Jancovici)
» Petites questions que je me pose auxquelles mon vilain prof de physique ne veut pas répondre :(
» Améliorons mode surdoué, le kit de survie de jean mi et jean michette :)
» Captain Levy
» Rencontre à la cité fertile 25,26,27 juin (Etienne Klein et Jean-Marc Jancovici)
» Petites questions que je me pose auxquelles mon vilain prof de physique ne veut pas répondre :(
» Améliorons mode surdoué, le kit de survie de jean mi et jean michette :)
» Captain Levy
Page 1 sur 4
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Évènements
Évènements