Re: Qui aime la physique ou les mathématiques?

par stupeflip666 Jeu 7 Jan 2016 - 14:12

paela a écrit: Si oui, aucun programme d'énumère une suite infinie car la mémoire est toujours finie.)

On parle de programmes théoriques qui ont accès à une mémoire non bornée. La théorie des programmes ayant une mémoire finie n'est pas très intéressante : C'est simplement la théorie des automates finis.

paela a écrit: -preuve claire de la proposition 0

Il suffit d'énumérer les programmes par ordre lexicographique. C'est du niveau CE1.

paela a écrit: -preuve de la proposition A

Si f(a) != g(a) alors f != g. Il te faut vraiment une preuve pour ça ?

par paela Jeu 7 Jan 2016 - 14:35

D'accord, que faut-il entendre par programme alors, machine de Turing?
Alors, comment construit-on la machine de Turing qui calcule 1 - S(n)(n)?

Ce que cette preuve montre presque dans ce contexte, c'est que l'ensemble des machines de Turing n'est pas récursif.

par fragmentation Jeu 7 Jan 2016 - 15:22

par stupeflip666 Jeu 7 Jan 2016 - 15:24

paela a écrit: D'accord, que faut-il entendre par programme alors, machine de Turing?

Par exemple oui, il y a plusieurs moyens de formaliser la notion de programme. Les machines de Turing, ou tu peux simplement dire que c'est un fichier texte (une suite finie de caractères) d'un programme en java par exemple.

paela a écrit: Alors, comment construit-on la machine de Turing qui calcule 1 - S(n)(n)?

C'est effectivement la question fondamentale, que l'auteur du post a laissé de coté. On pourrait dire naïvement que la machine de Turing en question (mais c'est plus simple de raisonner en terme de programme dans un langage de programmation classique) simule le programme S(0) jusqu'au moment où il génère le bit b, et envoie comme sortie ce bit b. Puis fait la même chose avec le programme S(1) jusqu'à ce qu'il génère son deuxième bit S(1)(1), et ainsi de suite... A première vue ce procédé semble marcher. Mais il laisse de coté le problème de savoir si par exemple le programme S(7) va réellement un jour générer sa sortie numéro 7 ou si il va rester bloquer à l'étape 6 dans une boucle infinie... Tout le problème est là.

paela a écrit: Ce que cette preuve montre presque dans ce contexte, c'est que l'ensemble des machines de Turing n'est pas récursif.

Mhhhh la preuve a un problème car elle oublie le point fondamental de l'"arrêt" ou de la "continuation" des programmes S(n). Mais sinon dans la réalité, les machines de Turing sont très faciles à énumérer, c'est énumérer leur sortie qui pose problème.....

par Stauk Jeu 7 Jan 2016 - 15:35

En effet, en l'état de la démonstration, on ne peut pas garantir que le programme x génère bien le bit de rang n. Je propose le procédé suivant pour fournir cette garantie :

Il suffit que S(n)(n) soit différent pour au moins un des programmes de la liste. Une fois qu'on a identifié le programme S(n) utilisé pour générer x(n), on peut le marquer et garantir qu'on ne l'utilise pas à nouveau.

x(n) peut donc être généré, dés lors qu'il est possible de trouver parmi la liste au moins un programme dont la production de S(n)(n) est bornée, et ceci quelque soit n. Si on se place dans l'ensemble de tous les programmes (qui génèrent des suites de 0 et 1), et qu'on prend S(n) la suite de ces programmes, alors x est bien définie pour tout n. (sauf à supposer qu'à partir d'un certain rang n fini, plus aucun programme de rang supérieur ne termine jamais ... ce qui semble absurde)

En effet pour chaque n, on applique le programme suivant :
Simuler les K premières instructions des K premiers programmes non encore marqués.
Si l'un des programmes s'arrête, alors l'utiliser (et le marquer) pour produire x(n) (si le programme s'arrête avant d'avoir produit 1 ou 0, on considère qu'il a produit 0). Sinon augmenter K.

par paela Jeu 7 Jan 2016 - 16:43

[quote]Par exemple oui, il y a plusieurs moyens de formaliser la notion de programme. Les machines de Turing, ou tu peux simplement dire que c'est un fichier texte (une suite finie de caractères) d'un programme en java par exemple.[/quote
Ce ne sont pas les mêmes choses, il y a un nombre fini de fichiers texte de programmes en Java.

Le problème de savoir si le programme S(n) va s'arrêter en n n'en est pas un: si on suppose que S est un programme qui énumère une suite d'entiers, on suppose qu'il s'arrête quelle que soit son entrée il me semble.

Là où il y a un souci, c'est dans la possibilité de faire appel au programme S(n) à partir de la donnée de n. Il faudrait avoir une partie du programme, disons un sous programme A(.) qui renvoie le code d,un certain programme de la liste noté S(p) en p, de telle manière que tout programme de la liste soit appelé une et une seule fois par A(.). Alors le programme global G(.) renvoie 1 - U(A(n),n) en n. Où U(.,.) est une machine de Turing universelle: si P est un programme de code p, et si d est une donnée de P, U(p,d) ne se termine pas si P(d) ne se termine pas, et renvoie le résultat de P(d) sinon.

Cette partie A(.) n'existe pas dans le cas des programmes (machines de Turing) qui énumèrent des suites de 0 et de 1. Et l'idée de Stauk permet de démontrer ça.

par fragmentation Jeu 7 Jan 2016 - 17:01

paela a écrit:
Là où il y a un souci, c'est dans la possibilité de faire appel au programme S(n) à partir de la donnée de n. Il faudrait avoir une partie du programme, disons un sous programme A(.) qui renvoie le code d,un certain programme de la liste noté S(p) en p, de telle manière que tout programme de la liste soit appelé une et une seule fois par A(.). Alors le programme global G(.) renvoie 1 - U(A(n),n) en n. Où U(.,.) est une machine de Turing universelle: si P est un programme de code p, et si d est une donnée de P, U(p,d) ne se termine pas si P(d) ne se termine pas, et renvoie le résultat de P(d) sinon.

Cette partie A(.) n'existe pas dans le cas des programmes (machines de Turing) qui énumèrent des suites de 0 et de 1. Et l'idée de Stauk permet de démontrer ça.

Je pense qu'il s'agit des programmes sans paramètre.
Est ce que tu es d'accord pour dire qu'un programme sans paramètre peut générer une suite infinie de 0 et de 1 ??

Dans la suite S(n), n n'est donc pas le paramètre, mais le numéro d'ordre du programme.
Un programme (sans paramètre) générant des suites de 1 et de 0 est une initialisation d'un nombre fini de bits d'une bande de turing, associé à une machine universelle de turing, avec un etat capable de produire 0, et un etat capable de produire 1. Pour simplifier, on parle juste de programme, c'est de toute manière connu pour être équivalent (etant entendu que le programme a accès une bande extensible à l'infini pour stocker ses données)

Edit :
Donc pour construire le programme x de stauk, il est sous entendu que son programme x (qui ne prend aucun paramètre) est capable de générer chaque élement des S(n) (qui sont peut être tout simplement les entiers, s'il s'agit de tous les programmes possibles). D'où le problème qu'on ne peut pas espérer déduire x d'une liste qui ne comporterait que les programmes qui terminent .... (ou ayant une propriété similaire).

par paela Jeu 7 Jan 2016 - 18:22

Je ne suis pas sûr de voir ce que tu veux dire par "générer". Si on parle bien de programmes théoriques, alors je pense qu'il est sage de se donner une définition parce qu'il n'est pas évident de formaliser cela mathématiquement. Heureusement, cela a été fait: il y a les machines de Turing.
Mais une machine de Turing a des "paramètres" ou est vide et ne "fait" rien.

En tout cas, j'ai bien voulu désigner un programme par S(n) dans mon message précédent.

Je n'ai pas compris l'édit. Ce que je peux dire, c'est que même si la liste de programmes dont on dispose contient aussi ceux qui ne se terminent pas pour toute valeur de leur paramètre, on peut en définissant G(.) identiquement à partir de la supposition de l´existence de A(.) montrer que A(.) ne peut pas exister dans ce cas non plus.

par fragmentation Ven 8 Jan 2016 - 1:01

@Stauk : tu ne prouves pas que le programme n appartient pas a la liste. Pour t en convaincre observe ce qui se passe quand x rencontre x... Il s oublie .. et n est au final pas different de lui meme.

par stupeflip666 Ven 8 Jan 2016 - 5:35

@Paela Le problème est simplement que tu manques un peu de culture sur la théorie de la calculabilité, mais certaines de tes remarques sont néanmoins très pertinentes.
Les programmes sans paramètres qui génèrent des suites infinies de bits font partie de la théorie et il n'y a aucun problème avec ça.
Il y a un nombre infini dénombrable de fichiers texte en java, c'est du niveau CE1 m'enfin Smile

Il y a une bijection naturelle entre les fichiers sources en java et les machines de Turing (=associer au programme java la MT qui fait la même chose). Si ce n'était pas le cas, les machines de Turing ne seraient pas un bon model de ce qu'est un programme !

Et pour finir oui, tu as raison, une manière de voir les choses est que l'ensemble des programmes=machines de Turing qui génèrent un suite infinie (et non pas finie) de bits n'est pas récursif=décidable. C'est ce que prouve la démonstration de @Stauk.

[EDIT] Et pourquoi cet ensemble n'est-il pas récursif ? La seule explication possible est que le problème de l'arrêt indécidable, car c'est l'ingrédient qui manque pour filter les programmes qui génèrent des suites infinies de bits parmi les programmes qui peuvent potentiellement générer des suites finies ou infinies de bits (Cet ensemble composite étant trivialement récursif).

par fragmentation Ven 8 Jan 2016 - 9:16

https://en.wikipedia.org/wiki/Presburger_arithmetic

Depuis 1929 il est possible prouver que certaines choses sont vrai ... et moi j apprends ca en 2016!!!
Vous le saviez ?? Les mathematiques decidables existent !!! Youpi tralala.

Mojżesz Presburger proved Presburger arithmetic to be:

consistent: There is no statement in Presburger arithmetic which can be deduced from the axioms such that its negation can also be deduced.
complete: For each statement in the language of Presburger arithmetic, either it is possible to deduce it from the axioms or it is possible to deduce its negation.
decidable: There exists an algorithm which decides whether any given statement in Presburger arithmetic is a theorem or a nontheorem.
The decidability of Presburger arithmetic can be shown using quantifier elimination, supplemented by reasoning about arithmetical congruence (Enderton 2001, p. 188).

http://math.stackexchange.com/questions/1109457/why-dont-we-use-presburgers-arithmetic-instead-of-peanos-arithmetic

http://mathoverflow.net/questions/19857/has-decidability-got-something-to-do-with-primes/19874#19874

par stupeflip666 Ven 8 Jan 2016 - 10:49

fragmentation a écrit:Depuis 1929 il est possible prouver que certaines choses sont vrai ... et moi j apprends ca en 2016!!!

Pour modérer un peu ton enthousiasme, disons qu'il est possible de démontrer dans le cadre d'une théorie non décidable et potentiellement inconsistante, qu'une certaine théorie sur les nombres entiers, qui laisse forcément de coté tout un tas de questions légitimes sur les nombres entiers (comme par exemple, est-ce que cette équation sur les nombres entiers admet une solution ?) est à la fois consistante et complète (complète sur son "ensemble de définition")

Je peux t'inventer en 2 secondes une théorie qui a exactement les mêmes propriétés.
Voici cette théorie, elle a exactement un axiome :
axiome 1 : 1+1=2

[EDIT] Et son ensemble de définition est exactement l'ensemble des formules suivantes :
formule 1 : 1+1=2

Elle est donc complète et consistante. (Je laisse en exercice la démonstration du fait qu'elle est consistante)

par fragmentation Ven 8 Jan 2016 - 11:04

stupeflip666 a écrit:
fragmentation a écrit:Depuis 1929 il est possible prouver que certaines choses sont vrai ... et moi j apprends ca en 2016!!!
Pour modérer un peu ton enthousiasme, disons qu'il est possible de démontrer dans le cadre d'une théorie non décidable et potentiellement inconsistante, qu'une certaine théorie sur les nombres entiers, qui laisse forcément de coté tout un tas de questions légitimes sur les nombres entiers (comme par exemple, est-ce que cette équation sur les nombres entiers admet une solution ?) est à la fois consistante et complète (complète sur son "ensemble de définition")
Je peux t'inventer en 2 secondes une théorie qui a exactement les mêmes propriétés.
Voici cette théorie, elle a exactement un axiome :
axiome 1 : 1+1=2
[EDIT] Et son ensemble de définition est exactement l'ensemble des formules suivantes :
formule 1 : 1+1=2
Elle est donc complète et consistante. (Je laisse en exercice la démonstration du fait qu'elle est consistante)

Ah mais oui, mais non !!!!
L'incomplétude des théories incomplètes est montrée aussi par ces même théories potentiellement inconsistantes ! Si on les évite, alors on peut avoir une théories, qui au moins est naivement complète, et qui dit des choses utiles. Comme d'affirmer que 1+1=2, et même de le généraliser. Et ensuite de permettre de prouver que 7x7=49. Et ça ta théorie certe complète et consistante, ne peut pas le prouver. (D'ailleurs le nombres de démonstrations est faibles dans ta théorie à toi). Par ailleurs, le fait qu'il existe une théorie consistante et complète naivement prouvable, capable de prouver certaines vérités non immédiates par un processus déductif (en fait il en existe plusieurs) est un point essentiel sur le plan philosophique. On m'a toujours fait douter que de présumer que 1+1=2 et que la fonction successeur existe, et que les déductions par induction fonctionnent, on m'a toujours dit : tu ne pourras jamais prouver qu'une théorie qui les utilises n'est pas autocontradictoire ...

Partant de là, on m'a fait douter de l'existence de toute vérité. Quand visiblement c'était très exagéré. La véracité ne devient douteuses, que si on commence à faire n'importe quoi. Comme de supposer que quelque soit n et m entier, alors n*m existe. Hahaha, et moi qui trouvait déjà le procédé diagonal un peu fumesque ! En fait c'est n*m qui était une grosse arnaque des qu'on accepte la fonction en successeur.

(bon je laisse ce brouillon)

par paela Ven 8 Jan 2016 - 14:04

@stupeflip666 : D'accord, je croyais que quand tu parlais d'un fichier texte en java, tu parlais vraiment d'un fichier texte, un truc que tu aurais sur ton ordi quoi.
Et effectivement la version du raisonnement où on accepte les programmes ne se terminant pas pour tout entier ne peut pas se faire sans moyen de déterminer si un programme ça s'arrêter ou pas. Cependant il faut supposer que l'ensemble des programmes est récursif pour montrer que son problème de l'arrêt n'est pas decidable. Et je ne vois toujours pas pourquoi on appelerait "programme qui énumère une suite de 0 et de 1" quelque chose qui par exemple ne termine en aucune valeur de sa donnée.

Il faut préciser un langage lorsqu'on parle de théorie complète, celle-ci ne l'est pas dans un langage contenant +. De même, il faut un minimum définir ce dont on parle si on veut traiter des questions de logique mathématiques qui sont souvent assez subtiles.

par Invité Ven 8 Jan 2016 - 17:00

il existe un méthode classique pour valider une hypothèse , y compris mathématique, c'est le raisonnement par l'absurde, ou la méthode hypothético déductive

résumable en "que se passerait il si ?" on peut poser que 1+1=2 est une relation fausse alors on devrait par exemple poser que le signe égal possède plusieurs interprétations dans des "univers d'hypothèses théoriques déterminées

cela est particulièrement flagrant si je pose

1+1=1+0.99+.0099+... à l'infini

où s'arrête t on ?

je pose que le signe égalité n'est qu'une convention valable dans une fourchette donnée

etc, ces méthodes dites par l'absurde sont d'une puissance sous estimée

par prométhéus Ven 8 Jan 2016 - 19:59

zebulonlezebre a écrit:il existe un méthode classique pour valider une hypothèse , y compris mathématique, c'est le raisonnement par l'absurde, ou la méthode hypothético déductive

Raisonnement par l'absurde ≠ méthode hypothético-déductive

zebulonlezebre a écrit:
etc, ces méthodes dites par l'absurde sont d'une puissance sous estimée

Mais d'une portée limitée...
http://www.entretemps.asso.fr/maths/Borceux.pdf

par Invité Ven 8 Jan 2016 - 20:49

"Raisonnement par l'absurde ≠ méthode hypothético-déductive"

oui et non.. l'absurde pose aussi parfois mais pas toujours des hypothèses à partir desquelles on déduit mais bon cela dépend de l'application bien évidemment je suis d'accord

pour la portée elle est puissante mais pas absolue en effet , sinon ce serait trop simple ;-) il faut innover et mélanger les méthodes des différents "univers" par exemple les distances minimales ou les surfaces minimales et leurs principes pourraient être a priori utiles par leur principe disons de "parcimonie" pour résoudre des calculs impliquant des intégrales ou des surfaces complexes

la démonstration mathématique de l'absence de perte d'énergie de deux vagues se croisant en océanographie pourrait très bien s'appliquer à certains croisements d'ondes de particules élémentaires , enfin là je suppose que c'est déjà appliqué

on a beaucoup à apprendre de l'interdisciplinarité je pense
et pourquoi pas de nouvelles méthodes de résolution à mettre en œuvre

j'ai lu récemment que les techniques de big data en marketing pourraient s'appliquer en astrophysique par exemple

http://www.e-marketing.fr/Thematique/digital-data-1004/Breves/Data-marketing-astrophysique-meme-combat-300459.htm#.VpAS4KRgm1s

par stupeflip666 Ven 8 Jan 2016 - 22:21

Ce thread est en train de partir en sucette !!!

par stupeflip666 Ven 8 Jan 2016 - 22:30

paela a écrit: Et je ne vois toujours pas pourquoi on appelerait "programme qui énumère une suite de 0 et de 1" quelque chose qui par exemple ne termine en aucune valeur de sa donnée.

ça n'a rien de mystérieux en fait. Si cela te dérange, tu peux remplacer "programme sans paramètre énumérant une suite infinie de bits" par "programme acceptant en paramètre un entier n et produisant un bit b". Les deux définitions sont exactement équivalentes, la relation étant évidemment que le programme de la deuxième définition produit à la demande le nième bit (n étant le paramètre) de la séquence produite par le programme de la première définition.

par paela Sam 9 Jan 2016 - 11:52

Je vois comment on fait le lien entre un programme avec un paramètre et un programme sans paramètre. (Cela dit, je trouve la première approche plus pratique)

Je fais la distinction entre un programme (avec un paramètre) qui étant donné son paramètre produit systématiquement un résultat (un programme qui s'arrête tout le temps), et un programme tourne en boucle pour certaines valeurs de ses paramètres.
Pour moi, un programme qui énumère une suite de bits est du premier type. C'est simplement une question de langage courant.

par Invité Sam 9 Jan 2016 - 21:44

stupeflip666 a écrit:Ce thread est en train de partir en sucette !!!

"en train", t'es bien gentil...

par fragmentation Ven 15 Jan 2016 - 0:18

paela a écrit:
Pour moi, un programme qui énumère une suite de bits est du premier type. C'est simplement une question de langage courant.

Supposer qu'un programme qui emets une suite de bits infinie quelconque termine toujours mène à une contradiction. (De même que de supposer qu'il est possibe de déterminer via un algorithme donné à priori qu'un programme termine, mène à une contradiction). Il est nécessaire pour éviter la contradiction que certains bits de la suite infinie prennent un temps infini pour être généré.

par paela Ven 15 Jan 2016 - 16:48

Je trouve plus simple de parler de programme qui prend un argument entier n et qui renvoie un bit b(n).
Supposer qu'il renvoie toujours un bit quel que soit n n'entraîne pas de contradiction.

par fragmentation Ven 15 Jan 2016 - 16:58

paela a écrit:Je trouve plus simple de parler de programme qui prend un argument entier n et qui renvoie un bit b(n).
Supposer qu'il renvoie toujours un bit quel que soit n n'entraîne pas de contradiction.

Ca suppose qu il termine pour tout n. Savoir si un programme termine est "indecidable" (dans le cas general )

par paela Ven 15 Jan 2016 - 17:02

Oui, oui, mais pourquoi appeler programme qui donne les valeurs d'une suite quelque chose qui bloque par exemple pour tout entier?

par fragmentation Ven 15 Jan 2016 - 21:32

paela a écrit:Oui, oui, mais pourquoi appeler programme qui donne les valeurs d'une suite quelque chose qui bloque par exemple pour tout entier?

Parceque sinon tu es obligé de démontrer que tu as le droit d'appeler le truc "programme", à chaque fois que tu veux nommer un truc. Et en général la démonstration est impossible ... (indécidable) ...

Je sais pas si j'ai bien tout compris, mais j'ai même l'impression que toutes les suites finies de 0 et de 1 ne sont pas générables par des programmes.

En effet, étant donné une instruction X (qui génère un nouvel élément de la suite), les programmes qui emploient cette instruction X pour générer des suites finies de taille non à priori bornée, ne peuvent pas tous générer les éléments de la suite associée en un temps fini. Si c'était le cas on peut prouver par diagonalisation que l'énumération de ces programmes ne contient pas tous ces programmes.

En reprennant la démonstration de stauk plus haut ... Les suites n'ont même pas besoin d'être infinies.
D'où la nécessité de considérer aussi les programmes qui ne génèrent rien. Juste du fait qu'il est impossible d'un point de vu rationnel de les distinguer à priori les uns des autres, sans soit en les observant soit en tombant par chance sur un programme analysable.

par stupeflip666 Ven 15 Jan 2016 - 21:37

fragmentation a écrit:Je sais pas si j'ai bien tout compris, mais j'ai même l'impression que toutes les suites finies de 0 et de 1 ne sont pas générables par des programmes.

Ben si quand même... Tu peux toujours écrire un programme qui contient explicitement la suite finie de bits Smile

par stupeflip666 Ven 15 Jan 2016 - 21:42

paela a écrit:Oui, oui, mais pourquoi appeler programme qui donne les valeurs d'une suite quelque chose qui bloque par exemple pour tout entier?

C'est juste un petit problème de légèreté linguistique. En réalité il faut parler de programmes qui peut potentiellement retourner un bit ou ne jamais rien retourner.

L'avantage c'est que cette classe de programmes est facilement décidable de manière "statique".

En revanche la classe des programmes qui retournent toujours un bit au bout d'un temps de calcul fini n'est pas décidable. Mais bien sûr ça n'interdit pas de parler de cet ensemble !

par fragmentation Ven 15 Jan 2016 - 21:47

stupeflip666 a écrit:
fragmentation a écrit:Je sais pas si j'ai bien tout compris, mais j'ai même l'impression que toutes les suites finies de 0 et de 1 ne sont pas générables par des programmes.
Ben si quand même... Tu peux toujours écrire un programme qui contient explicitement la suite finie de bits

Ah oui, le programme qui les utilise pour générer la suite diagonale perd la propriété "suite finie", en générant alors une suite infinie. Quel monde étrange. Puisque du coup on peut continuer à générer des programmes générant des suites infinies, par diagonalisation, qui mécaniquement terminent tous, et qui sont tous garantis comme étant différents. Du coup on peut construire une infinité de programmes générant des suites infinies, qui ont tous la garantie d'être différents les uns des autres.

Et par conséquent, il est possible de lister tous les programmes qui sont générés par ce procédé, avec une simple suite. Mais du coup, il existe un programme qui génère des suites infinies qui ne fait pas partie de cette suite .... (procédé diagonal utilisé plus haut par stauk).

Donc pour le moment, je maintiens qu'il faut un argument pour que tu puisses affirmer péremptoirement que ces programmes générant des listes finies avec un nombre d'éléments à prioris non bornés existent bien (sous une forme listable) .... puisque du haut de mon etat de fatigue actuel, ça m'a tout l'air d'être parfaitement contradictoire.

par stupeflip666 Ven 15 Jan 2016 - 21:52

fragmentation a écrit:Et par conséquent, il est possible de lister tous les programmes qui sont générés par ce procédé, avec une simple suite. Mais du coup, il existe un programme qui génère des suites infinies qui ne fait pas partie de cette suite .... (procédé diagonal utilisé plus haut par stauk).

Je n'ai rien compris. Mais à mon avis le problème est toujours et encore le fait que tu ne prends pas en considération que le problème de l'arrêt est indécidable.

par Stauk Sam 16 Jan 2016 - 10:03

stupeflip666 a écrit:
fragmentation a écrit:Et par conséquent, il est possible de lister tous les programmes qui sont générés par ce procédé, avec une simple suite. Mais du coup, il existe un programme qui génère des suites infinies qui ne fait pas partie de cette suite .... (procédé diagonal utilisé plus haut par stauk).

Je n'ai rien compris. Mais à mon avis le problème est toujours et encore le fait que tu ne prends pas en considération que le problème de l'arrêt est indécidable.

Mmm, on peut utiliser ce procédé pour créer une suite intriguante.

Considérons donc ce programme qui va tout d'abord diagonaliser les nombres entiers, et ainsi obtenir une chaine infinie binaire. Il lui est ensuite possible d'insérer ce nouvel élément de façon pseudo aléatoire dans la liste déjà existante (Par exemple en utilisant les décimales de pi comme générateur, ou bien la séquence des nombres premiers). Il est donc possible de créer ainsi une infinité de réels.

Tu vas objecter donc que de lister le nouveau nombre réel inséré prend une éternité, mais en fait on peut trouver des procédés qui permettent de générer une infinité de nombres réels, pour autant qu'on garantisse que chaque décimale est produite dans un temps garanti fini. Or le procédé de diagonalisation sur les entiers a bien cette propriété. Pour chaque nombre créé, il est possible de tirer aléatoirement son rang futur, et de déclencher dès qu'on connait celui ci la création du réel suivant. Si ce réel suivant arrive au rang d'un des réels précédent nécessaire à sa construction au moment de construire sa décimale, il lui suffira d'attendre qu'elle soit produite, car on a cette garantie que cela arrivera.

Naturellement il y a peut être encore plus simple d'ailleurs. Qui serait simplement de générer par diagonalisation une infinité de réels (c'est à dire de 0/1), en utilisant le générateur pseudo-aléatoire sus décrit. Passer par les nombres entiers ne semble pas apporter grand chose à l'histoire. Si on arrive à construire l'ensemble des suites infinies de 1 et de 0 dont chaque 0/1 a la caractéristique d'être parfaitement aléatoire, je me demande bien ce qu'on peut attendre de plus des développement des réels.

En particulier en considérant une suite particulière de 0 et de 1, dés lors qu'on a généré toutes les suites aléatoires possibles, il semble contre intuitif d'affirmer que le nouveau réel n'appartient en effet pas à la liste. Bien sûr on peut appliquer à cette liste infinie de réels tous aléatoires le procédé diagonal. Toutefois le problème de l'arrêt des programmes, montre que d'appliquer naivement le procédé diagonal ne garanti pas toujours un résultat. En effet on a montré précédemment qu'un programme qui tenterait de l'appliquer à l'ensemble des programmes (donc des nombres entiers) rencontrera des difficultés à le faire qui rendront ce procédé diagonal lorsqu'il est appliqué par un programme, possiblement non capable de conclure à la non appartenance définitive d'un nouvel élément à une liste pré-existante.

En d'autres termes, cela suggère que le procédé diagonal ne doit être utilisé, que tant que l'on peut prouver qu'il existe bien un programme capable d'employer ce procédé, lorsqu'un tel programme n'existe pas, je ne vois pas en quoi il est justifié de déclarer que le procédé est tout de même applicable. Car il s'agit bien d'un algorithme, un algorithme auquel on tente de faire générer une suite de 0 et de 1, qui ne serait pas déjà dans la liste. Le procédé diagonal doit donc être justifié par l'existence du programme qui lui correspond.

Dans le cas où on génererait dans un temps garanti fini chaque décimale d'un ensemble infini de réels dont chaque décimale est tiré aléatoirement en utilisant un procédé diagonal, et puisque chacune de ces décimales est bien garantie générée dans un temps fini, il est bien possible d'appliquer le procédé diagonal, pour tenter de créer un nouvel élément, mais a t'on encore cette garantie qu'il va terminer ? De même qu'un programme qui essaye de se simuler lui même n'arrive jamais à modifier par avance le résultat qu'il va fournir, de même ici le procédé diagonal essaye de s'appliquer à lui même.

Mais alors cela signifirait qu'on ne peut pas toujours générer un nouvel élément en utilisant le procédé diagonal. Ce qui n'est pas très étonnant s'il s'agit bien d'un algorithme. Et si le procédé diagonal n'est pas un algorithme, alors je demande en quoi c'est un argument.

Sur ce, j'ai l'impression d'avoir trouvé un procédé pour construire une forme arrondie (c'est à dire conforme à la distance euclidienne) en utilisant des automates cellulaires sur une grille gauche/droit haut/bas. J'ai en effet créé un programme qui prend un point d'origine, et qui fait démarer des automates se déplaçant à chaque itération avec un mouvement brownien. Un automate qui arrive sur une nouvelle cellule, augmente de 1 le compteur de la cellule. Après un grand nombre (potentiellement infini) de passage d'un grand nombre d'automate l'image obtenue suggère qu'on obtient de jolie courbes de niveaux, un peu irrégulières mais manifestement rondes. (on voit l'une de ces images sur mon avatar actuel, mis en ligne aujourd'hui).

Est ce que quelqu'un peut me confirmer, ou m' infirmer cette hypothèse de circularité des courbes de niveaux ainsi générées ? (ca doit être la limité d'une somme de probabilité, je présumé, qui pour certains matheux serait aisée à calculer ... quand à moi je préfère simuler les choses : c'est plus simple. Et souvent ça donne beaucoup d'information également.

par Invité Sam 16 Jan 2016 - 10:17

Pffff.... même ici, y'a des tartines...

Hier, sur France Culture, il y avait ça:

Quelle physique enseigne-t-on aujourd'hui?

par Invité Sam 16 Jan 2016 - 14:02

Stauk a écrit:
Sur ce, j'ai l'impression d'avoir trouvé un procédé pour construire une forme arrondie (c'est à dire conforme à la distance euclidienne) en utilisant des automates cellulaires sur une grille gauche/droit haut/bas. J'ai en effet créé un programme qui prend un point d'origine, et qui fait démarer des automates se déplaçant à chaque itération avec un mouvement brownien. Un automate qui arrive sur une nouvelle cellule, augmente de 1 le compteur de la cellule. Après un grand nombre (potentiellement infini) de passage d'un grand nombre d'automate l'image obtenue suggère qu'on obtient de jolie courbes de niveaux, un peu irrégulières mais manifestement rondes. (on voit l'une de ces images sur mon avatar actuel, mis en ligne aujourd'hui).

Est ce que quelqu'un peut me confirmer, ou m' infirmer cette hypothèse de circularité des courbes de niveaux ainsi générées ? (ca doit être la limité d'une somme de probabilité, je présumé, qui pour certains matheux serait aisée à calculer ... quand à moi je préfère simuler les choses : c'est plus simple. Et souvent ça donne beaucoup d'information également.

Ben oui, c'est la base des opérateurs de diffusion issus de la moyenne des équations de Boltzmann...

De toutes façons, si c'est brownien, c'est isotrope, donc forcément à symétrie sphérique, pas besoin de s'amuser à simuler ni à calculer...

Ce que tu viens de faire n'est rien d'autre que la fonction densité de probabilité (ou la NDF si tu n'as pas normalisé) de la distance parcourue. Pas besoin de se prendre la tete ou partir dans des équations imbuvables, c'est connu depuis quasiment 1 siècle. Tout ça pour démystifier un peu ce que tu dis, on a l'impression que c'est d'une extraordinaire complexité, à la limite de l'incompréhension humaine, alors que c'est franchement tout bête...

Stauk a écrit:quand à moi je préfère simuler les choses : c'est plus simple. Et souvent ça donne beaucoup d'information également.

Quant il sagit de trucs simplistes comme ça, d'accord, mais :
- la simulation ne te donne qu'un cas particulier, la démonstration sera bien plus généraliste
- là il sagit d'un truc simpliste, la simulation quand tu pars dans des trucs un peu plus sioux, c'est un métier, et ça ne se fait pas aussi facilement.

par stupeflip666 Sam 16 Jan 2016 - 20:33

hobb a écrit:
Ben oui, c'est la base des opérateurs de diffusion issus de la moyenne des équations de Boltzmann...

De toutes façons, si c'est brownien, c'est isotrope, donc forcément à symétrie sphérique, pas besoin de s'amuser à simuler ni à calculer...

Pour ma part, je ne vois pas comment une lattice 2d peut avoir une symétrie sphérique. Au minimum, le fait qu'une forme circulaire puisse émerger d'un tel truc à grande échelle est surprenant.

par Invité Sam 16 Jan 2016 - 20:36

Symétrie centrale si tu préfères. Et la densité de probabilité est nécessairement radialement décroissante en partant du point d'origine. Je ne vois pas le problème en fait...

Si la particule va d'un coté, si la probabilité n'était pas radialement décroissante, il faudrait qu'elle aille "équilibrer" sa proba de présence de l'autre coté, et devra donc passer par des cases plus proches du centre (statistiquement) pour y parvenir.

par stupeflip666 Sam 16 Jan 2016 - 20:48

hobb a écrit:Symétrie centrale si tu préfères. Et la densité de probabilité est nécessairement radialement décroissante en partant du point d'origine. Je ne vois pas le problème en fait...

Si la particule va d'un coté, si la probabilité n'était pas radialement décroissante, il faudrait qu'elle aille "équilibrer" sa proba de présence de l'autre coté, et devra donc passer par des cases plus proches du centre (statistiquement) pour y parvenir.

D'accord, mais je ne vois pas, naïvement, ce qui empêcherait par exemple d'obtenir des carrés imbriqués les uns dans les autres, et pas des cercles. Sachant qu'on part d'un truc carré à la base (les cellules de la lattice sont carrées) cela semblerait même plus naturel. D'autre part, cette symétrie centrale ne peut être qu’approximative : Si on regarde de très près ce qui se passe autour de la cellule centrale d'où part le "mobile", on a un quadrillage avec des gros carrés. Tu ne peux pas avoir de symétrie centrale sur un quadrillage 5x5 par exemple : au mieux un truc qui y ressemble vaguement.

par Invité Dim 17 Jan 2016 - 11:48

stupeflip666 a écrit:
D'accord, mais je ne vois pas, naïvement, ce qui empêcherait par exemple d'obtenir des carrés imbriqués les uns dans les autres, et pas des cercles. Sachant qu'on part d'un truc carré à la base (les cellules de la lattice sont carrées) cela semblerait même plus naturel. D'autre part, cette symétrie centrale ne peut être qu’approximative : Si on regarde de très près ce qui se passe autour de la cellule centrale d'où part le "mobile", on a un quadrillage avec des gros carrés. Tu ne peux pas avoir de symétrie centrale sur un quadrillage 5x5 par exemple : au mieux un truc qui y ressemble vaguement.

Ressembler vaguement... plus que ça meme, ça sera à symétrie sphérique, meme sur un 5x5. C'est la moyenne que tu appliques dessus qui est carrée, si le mouvement est brownien, il est parfaitement isotrope, et donc le résultat est à symétrie sphérique. Je ne vois vraiment pas le problème là... Un opérateur de diffusion sur un maillage carré te donne une diffusion sphérique, et encore heureux...

par stupeflip666 Dim 17 Jan 2016 - 15:06

hobb a écrit:Ressembler vaguement... plus que ça meme, ça sera à symétrie sphérique, meme sur un 5x5. C'est la moyenne que tu appliques dessus qui est carrée, si le mouvement est brownien, il est parfaitement isotrope, et donc le résultat est à symétrie sphérique. Je ne vois vraiment pas le problème là... Un opérateur de diffusion sur un maillage carré te donne une diffusion sphérique, et encore heureux...

Mais c'est toi qui parle d'opérateur de diffusion et tout ça. As tu seulement lu le message d'origine ? Il est question de marche aléatoire sur une grille 2d avec des cases carrées. Le mobile peut soit aller à gauche, à droite, en haut ou en bas. Je ne vois pas à priori de symétrie sphérique là dedans.
Quand à savoir si un opérateur de diffusion donne une diffusion sphérique, je n'en ai pas la moindre idée. Je ne suis pas expert dans le domaine, je ne sais même pas ce qu'est un "opérateur de diffusion" !
Donc est-ce que la règle de l'automate cellulaire décrit par l'auteur constitue un opérateur de diffusion ?
Si la réponse est non, il me semble que tous tes posts sont à coté de la plaque.
Si la réponse est oui, tu as juste dis que c'était évident parce que c'est évident :

hobb a écrit:Un opérateur de diffusion sur un maillage carré te donne une diffusion sphérique, et encore heureux

par Invité Dim 17 Jan 2016 - 17:47

stupeflip666 a écrit:
Mais c'est toi qui parle d'opérateur de diffusion et tout ça. As tu seulement lu le message d'origine ? Il est question de marche aléatoire sur une grille 2d avec des cases carrées.

Ben c'est comme ça que c'est calculé, les opérateurs de diffusion, donc oui, c'est pour ça que j'en parle. C'est par un coefficient de diffusion que les marches aléatoires sont caractérisées...

stupeflip666 a écrit:
Quand à savoir si un opérateur de diffusion donne une diffusion sphérique, je n'en ai pas la moindre idée. Je ne suis pas expert dans le domaine, je ne sais même pas ce qu'est un "opérateur de diffusion" !

Pourtant c'est la base des mouvements browniens, qui initiallement ont été étudiés pour la diffusion dans les gaz : https://fr.wikipedia.org/wiki/Mouvement_brownien

stupeflip666 a écrit:
Donc est-ce que la règle de l'automate cellulaire décrit par l'auteur constitue un opérateur de diffusion ?
Si la réponse est non, il me semble que tous tes posts sont à coté de la plaque.

La réponse est : oui.

stupeflip666 a écrit:
Si la réponse est oui, tu as juste dis que c'était évident parce que c'est évident :

Je dis juste que de part le principe de Curie, à causes symétriques, conséquences symétriques (si les opérateurs le sont, et là comme c'est un mouvement brownien, c'est isotrope, donc aussi à symétrie). Après pour l'isotropie de sa méthode, si ça ne l'est pas, alors ce n'est pas un mouvement brownien. 'Faut etre rigoureux aussi dans ce que l'on dit... Mais meme si elle ne l'est pas, lors de simulations numériques, les calculs de dérivées (secondes aussi, PUISQU'IL sagit de diffusion, et que ce sont dont les dérivées à l'ordre 2 qui caractérisent la vitesse d'étalement spatial du mélange) conservent la symétrie et l'isotropie du phénomène. Le résultat est évidement à symétrie sphérique puisque fondamentalement indépendant du maillage. C'est la base du calcul numérique.

par stupeflip666 Dim 17 Jan 2016 - 20:26

hobb a écrit: Après pour l'isotropie de sa méthode, si ça ne l'est pas, alors ce n'est pas un mouvement brownien. 'Faut etre rigoureux aussi dans ce que l'on dit

Visiblement pour l'auteur, mouvement brownien n'implique pas forcément symétrie sphérique, sinon il n'aurait pas pu s'étonner d'obtenir un truc à symétrie sphérique. Faut faire preuve de bon sens aussi. Pour moi un mouvement brownien c'est un truc qui bouge de manière aléatoire. C'est le cas d'un mobile qui choisit à chaque étape une direction parmi {gauche,droite,bas,haut} avec une probabilité 1/4 pour chaque cas. Encore une fois je ne vois pas de symétrie sphérique là dedans. Par exemple les diagonales sont différentes des horizontales, verticales, ne serait-ce que parce qu'il faut deux étapes pour y accéder.
Dirais-tu que le jeu d'échec a une symétrie sphérique ? Ou un meilleur exemple, othelo/réversi, le jeu de go ? Je vois des symétries centrales, des axes de symétries, mais pas de symétrie sphérique dans tout ça. Ne serait-ce que parce que dans tous ces cas, les diagonales sont manifestement différentes des horizontales.

hobb a écrit:. Le résultat est évidement à symétrie sphérique puisque fondamentalement indépendant du maillage. C'est la base du calcul numérique.

Et comment sait-on que le résultat est indépendant du maillage ? Il semble que tu ne fasses rien d'autre que répéter "c'est évident parce que c'est évident, c'est la base du calcul numérique, etc...".

par Invité Dim 17 Jan 2016 - 20:52

stupeflip666 a écrit:
Visiblement pour l'auteur, mouvement brownien n'implique pas forcément symétrie sphérique, sinon il n'aurait pas pu s'étonner d'obtenir un truc à symétrie sphérique. Faut faire preuve de bon sens aussi. Pour moi un mouvement brownien c'est un truc qui bouge de manière aléatoire. C'est le cas d'un mobile qui choisit à chaque étape une direction parmi {gauche,droite,bas,haut} avec une probabilité 1/4 pour chaque cas.

Faisons preuve de bon sens : dans ce cas ce n'est pas un mouvement brownien. Si l'auteur s'amuse à changer les définitions, c'est lui que ça regarde, il ne faudra dans ce cas pas s'étonner des incompréhensions dans les dialogues qui suivent.

stupeflip666 a écrit:
Encore une fois je ne vois pas de symétrie sphérique là dedans. Par exemple les diagonales sont différentes des horizontales, verticales, ne serait-ce que parce qu'il faut deux étapes pour y accéder.
Dirais-tu que le jeu d'échec a une symétrie sphérique ? Ou un meilleur exemple, othelo/réversi, le jeu de go ? Je vois des symétries centrales, des axes de symétries, mais pas de symétrie sphérique dans tout ça. Ne serait-ce que parce que dans tous ces cas, les diagonales sont manifestement différentes des horizontales.

L'explication de la symétrie sphérique vient de mon message précédent, concernant la différenciation sur chaque direction d'un opérateur du second ordre, qui donne un résultat à symétrie sphérique. Les opérateurs d'ordre 2 sont physiquement équivalents à des diffusions, et les diffusions, c'est à symétrie sphérique, puisqu'isotropes. Quand on simule une diffusion en 2 ou 3D, on calcule le terme selon X et Y, pas selon les diagonales (pour les schémas différence finie). Hé bien spliter l'opérateur en 2 directions ne modifie rien. C'est un opérateur isotrope, on le coupe en 2 : un par direction, ben ça donne la meme chose : donc on conserve la symétrie sphérique, c'est tout. Le commutateur est nul, donc je ne vois pas en quoi spliter (donc faire une marche aléatoire N/S/E/O au lieu d'un mouvement brownien) changerait quoique ce soit sur la symétrie...

Enfin bref.

par stupeflip666 Dim 17 Jan 2016 - 21:05

hobb a écrit:L'explication de la symétrie sphérique vient de mon message précédent, concernant la différenciation sur chaque direction d'un opérateur du second ordre, qui donne un résultat à symétrie sphérique. Les opérateurs d'ordre 2 sont physiquement équivalents à des diffusions, et les diffusions, c'est à symétrie sphérique, puisqu'isotropes. Quand on simule une diffusion en 2 ou 3D, on calcule le terme selon X et Y, pas selon les diagonales (pour les schémas différence finie). Hé bien spliter l'opérateur en 2 directions ne modifie rien. C'est un opérateur isotrope, on le coupe en 2 : un par direction, ben ça donne la meme chose : donc on conserve la symétrie sphérique, c'est tout. Le commutateur est nul, donc je ne vois pas en quoi spliter (donc faire une marche aléatoire N/S/E/O au lieu d'un mouvement brownien) changerait quoique ce soit sur la symétrie...
Enfin bref.

Voilà enfin quelque chose qui ressemble vaguement à une réelle tentative d'explication. On voit immédiatement que contrairement à ce qu'insinuent tes précédents messages, tout ça n'est en rien évident. Pour être franc, je n'ai absolument rien compris, mais j'imagine que ce que tu essayes d'expliquer doit être la bonne piste.

par Invité Dim 17 Jan 2016 - 21:44

On va essayer autrement. Tu prends une particule avec un mouvement brownien (un vrai). Tu la fais commencer au centre d'une cellule. La probabilité pour qu'elle passe sur une des cellules d'à coté est de 1 sur 4 (la proba pour qu'elle aille dans une des mailles diagonales sans passer par une des autres est strictement nulle). Faire du N/S/E/O revient donc à modéliser le comportement moyen d'un mouvement brownien (peu importe le temps qu'il lui faut pour changer de cellule, à un moment elle en changera forcément), et dans ce cas conservera la symétrie.

par stupeflip666 Dim 17 Jan 2016 - 21:55

Là je commence à comprendre, c'est beaucoup plus clair. Mais la particule n'arrive pas forcément au centre de la cellule, ça fait quand même une différence avec un vrai mouvement brownien. Pas évident de voir que ça n'aura pas d'incidence. (Un vrai mouvement brownien, si j'ai bien compris, c'est quand tous les angles de déplacement sont autorisés, y compris 12.565° par ex, mais la distance parcourue à chaque étape est fixe)

par Invité Dim 17 Jan 2016 - 21:57

Pour le brownien, la distance parcourue à chaque étape peut etre aléatoire aussi. C'est aussi pour ça qu'on définit le libre parcours moyen (qui est une fonction du coefficient de diffusion, etc : tout ça c'est corrélé par des lois stochastiques bien définies).

par stupeflip666 Dim 17 Jan 2016 - 22:03

Ouep ok.
ça commence à faire sens dans ma tête qu'il y aura une symétrie sphérique du fait de l'équivalence avec un "vrai" mouvement brownien où toutes les directions sont autorisées.

par Stauk Dim 17 Jan 2016 - 22:34

@Stupeflip666

https://en.wikipedia.org/wiki/Random_walk a écrit:
A Wiener process enjoys many symmetries random walk does not. For example, a Wiener process walk is invariant to rotations, but random walk is not, since the underlying grid is not (random walk is invariant to rotations by 90 degrees, but Wiener processes are invariant to rotations by, for example, 17 degrees too). This means that in many cases, problems on random walk are easier to solve by translating them to a Wiener process, solving the problem there, and then translating back. On the other hand, some problems are easier to solve with random walks due to its discrete nature.

Tu as bien du courage d'essayer d'extraire de l' information du sieur Hobb. Il est (probablement) doté d'une culture assez large en physique, mais sa façon de s'exprimer rend habituelement complètement stérile toute tentative d'extraire la moindre information de ses propos. Sauf concernant son état émotionnel, mais en général sur le plan technique, ça ne donne de liens vers aucune référence.

@Hobb : je te remercie de m'épargner l'effort de devoir tenter de faire de la divination concernant tes propos à l'avenir, par exemple en évitant d'intervenir en réponse à mes messages qui comporteraient une volonté de ma part de m'informer sur un sujet. La lecture du caractère méprisant étant une barrière déjà bien désagréable à franchir, y compris quand la personne sait être claire et informative, elle devient l'épitome du masochisme, quand il n'y a trop souvent rien à tirer.

par Invité Dim 17 Jan 2016 - 23:00

Stauk a écrit:mais en général sur le plan technique, ça ne donne de liens vers aucune référence.

L'apprentissage ça passe aussi par la recherche. Ca ne tombe pas tout cuit dans le bec. Et très franchement si je devais justifier toutes mes phrases, je pense que ça serait encore plus imbitable. Après si le but est de remettre systématiquement en cause ce que je dis, ben démerdez vous, personnelement je n'ai pas besoin de vous pour avancer, et ce n'est pas votre jugement que je prendrai en considération sur ce genre de chose.

Stauk a écrit:
Tu as bien du courage d'essayer d'extraire de l' information du sieur Hobb. Il est (probablement) doté d'une culture assez large en physique, mais sa façon de s'exprimer rend habituelement complètement stérile toute tentative d'extraire la moindre information de ses propos.

De la nuance entre "tenter d'extraire une information" et remettre en cause systématiquement tes interlocuteurs.

Juste qu'un peu d'humilité sur certains trucs ne te ferrait pas de mal. On a l'impression que tu révolutionne la science à chaque phrase que tu fait. Et contrairement à ce que tu dis, ce que tu écris ici n'est pas pour comprendre, mais par fierté personnelle, pour mettre un résultat comme ça comme avatar... Tu veux qu'on reparle du paradoxe des jumeaux, ou comme tu ne comprends pas et tu ne veux pas l'admettre, le seul truc que tu fais est de complexifier un truc déjà incompris pas et de tenter de me décrédibiliser (en me défiant de résoudre ton "problème") pour ne pas avoir à chercher à comprendre et/ou admettre que tu ne connais pas ? Alors ne viens pas dire que ce que tu postes, c'est toujours "par curiosité".
Tu t'épates de trouver un truc à symétrie sphérique avec un code qui tient en 5 lignes qu'on file en exo en première année de fac, pas de quoi penser trouver un truc révolutionnaire... D'autres seront peut etre épatés par ce que tu dis, désolé si ce n'est pas mon cas. Ce truc, on est des milliers à l'utiliser tous les jours, depuis des années.

par Invité Dim 17 Jan 2016 - 23:05

interlude coucou :

par Dubble Lun 18 Jan 2016 - 2:24

Bonsoir
En diagonale j'ai lu le mot "information" du coup ça m'a fait repenser à un truc :
Dans un texte, si j'e.lèv. alé.to.reme.t ce.tain.s l.t.rs, la co.pré.ens.on re.te cor.ect. . Du coup, on peut trouver une limite au % de lettres qu'on peut enlever sans "trop" perdre en compréhension.
Et une fois qu'on a trouvé ça, on peut en déduire quelle est "l'efficacité" du langage écrit.
Ca marche aussi dans une discussion, etc..

Et finalement on en déduit un débit d'information !

par Stauk Lun 18 Jan 2016 - 11:20

Une simulation avec les courbes de niveaux théoriques, et un choix de couleurs qui laisse voir les détails. (On reconnait parfaitement la symétrie sphérique évidente, aimablement pointée par hobb - enfin ... moi pas, mais j'imagine que pour le reste du monde c'est évident et ne mérite donc aucune autre explication que "c'est évident")
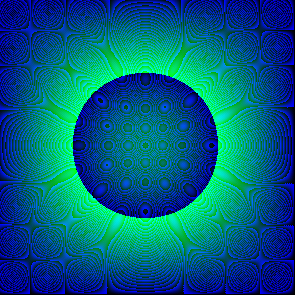
Qui aime la physique ou les mathématiques? - Page 4 1cold10

Qui aime la physique ou les mathématiques? - Page 4 1cold10

Une autre avec deux sources de diffusions au lieu d'une seule
A gauche au début du processus de diffusion, à droite plus tard dans le processus. (Refroidissement)
Qui aime la physique ou les mathématiques? - Page 4 2sourc10

Qui aime la physique ou les mathématiques? - Page 4 2sourc10

Qui aime la physique ou les mathématiques? - Page 4 2cold10